基于虚拟检测函数下的IMM-UKF机动目标跟踪*
2015-02-22徐洋徐松涛罗文涛向建军秦占师
徐洋,徐松涛,罗文涛,向建军,秦占师
(空军工程大学航空航天工程学院,西安710038)
基于虚拟检测函数下的IMM-UKF机动目标跟踪*
徐洋,徐松涛,罗文涛,向建军,秦占师
(空军工程大学航空航天工程学院,西安710038)
为了有效提高对机动目标的跟踪效果,将无迹卡尔曼滤波(UKF)引入到交互多模型(IMM)算法框架内,加强状态估计精度;引入强跟踪滤波器(STF)到UKF算法中,避免对强机动目标的过大时间延迟和跟踪性能差的缺点;提出虚拟检测函数法,在跟踪过程中自适应调整“当前”统计模型的机动参数,加大模型集与目标真实运动模式匹配概率。仿真结果验证了改进算法的有效性。
无迹卡尔曼滤波,交互式多模型,强跟踪滤波器,虚拟检测函数,机动参数
0 引言
机动目标的跟踪问题一直是人们研究的重点与难点,其研究困难主要来源于两种不确定性:一是目标运动方式的不确定性;二是量测起源的不确定性。在跟踪器设计过程中,目标模型的选择将直接关系到滤波性能的好坏,一般来说,目标做直线匀速运动时,跟踪问题很容易实现,但当目标发生强机动或快速机动时,由于无法准确预知目标下一时刻的运动状态,跟踪变得更加困难。
实现机动目标精确跟踪,首要解决的问题就是使建立的目标运动模型与实际的目标运动模型匹配。目前常用的有多模型(MM),交互式多模型(IMM),切换模型等。多模型方法就是用一组具有不同机动模型的滤波器分别进行跟踪滤波,最终的参数估计是各滤波器估计值的加权和;在多模型基础上,Shalom提出了交互式多模型方法,这一方法对无序目标的机动检测,显示了更好的鲁棒性和跟踪的稳定性;切换模型则是分别建立机动和非机动运动模型,利用机动检测实现在这两个模型之间的切换。一般来说,交互式多模型的跟踪性能较好[1-3]。
但IMM算法仍存在不足,如机动参数不能实时更新、多模型之间的竞争问题[4-6]等。针对以上不足,本文提出了一种针对强机动目标的跟踪方法,将UKF应用到IMM框架内,采用对于机动目标跟踪性能较好的CS模型作为模型集参考模型之一,结合CV模型和拐弯模型CT对目标进行联合跟踪;在UKF滤波步骤内引入强跟踪滤波器(STF),动态调整UKF算法中的协方差矩阵,间接调整增益矩阵,迫使残差序列具有正交性;提出一种虚拟检测函数法,根据新息均方值与虚拟新息协方差矩阵变化幅度之比,判断机动目标运动情况,实时调整CS模型的机动参数,提高总体的跟踪性能。
1 基于UKF的IMM滤波算法
IMM算法状态方程和量测方程如下:
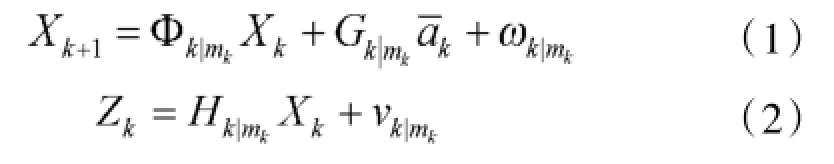
基于UKF的IMM滤波算法的每一个递归循环,共包括4步:输入交互、模型滤波计算、模型概率更新、输出交互。
1.1输入交互
利用上一个循环得到的所有状态及模型条件概率,为每个模型重新计算输入状态、输入状态误差协方差阵。
输入状态向量:
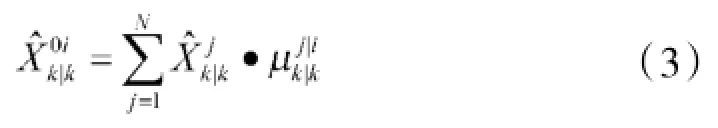
输入状态协方差:
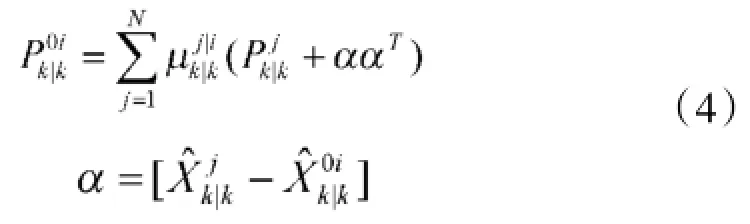
各个模型条件概率:
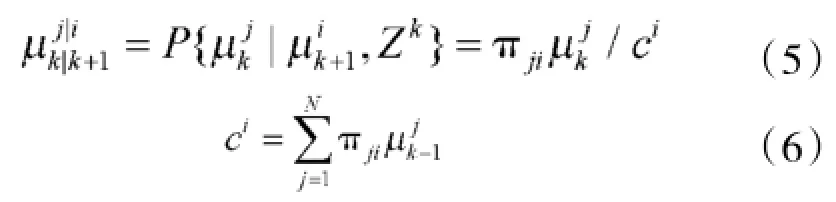
其中,μki代表在k时刻模型为mi的概率,μki= P{mki|在k}。
1.2各个模型滤波计算

aΩmax和a-Ωmax分别是Ω方向上正向和反向最大加速度,QiΩ0的取值可参考文献[1]。
③量测更新
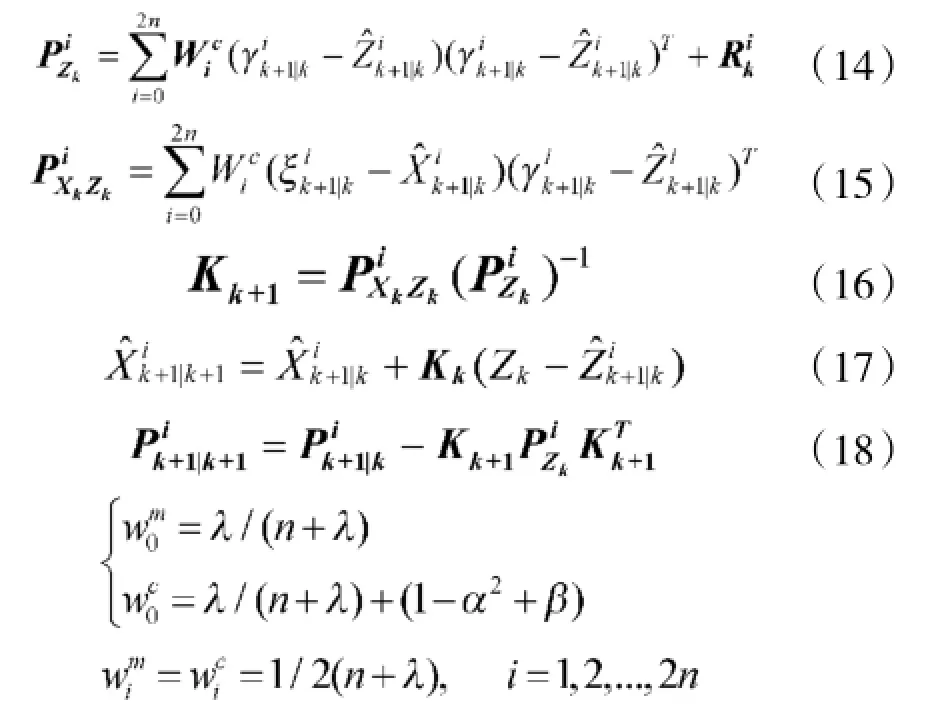
其中,λ=α2(n+k)-n,α决定Sigma点的散布程度,通常取一小的正值,k通常取0;β用来描述x的分布信息,在高斯情况下,β的最优值为2;wim为均值的权值,wic为方差的权值。
1.3模型概率更新
模型概率表明在某一时刻各模型匹配当前模式的概率,可由贝叶斯定理给出。模型概率更新方程为:
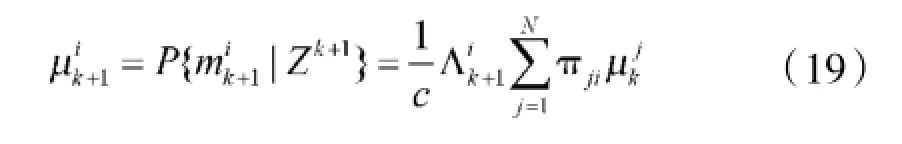
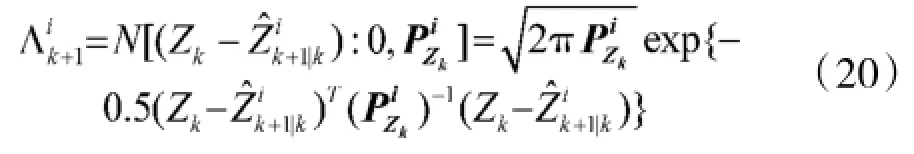
1.4输出交互
由所有子模型的状态估计加权得到最终的状态估计量:
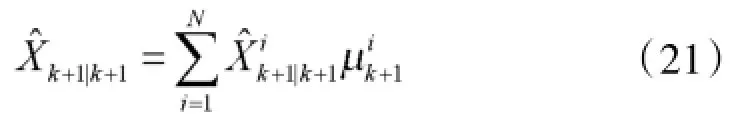
估计协方差阵;
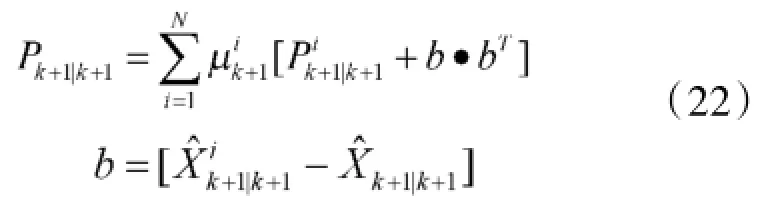
其模型结构如图1所示:
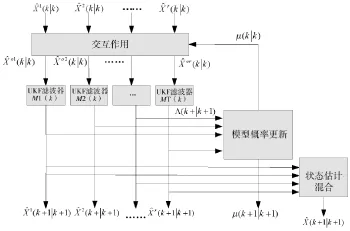
图1 IMM算法结构流程图
在标准IMM算法中,模型集是需要预先确定的。但在模型集选择过程中也存在着矛盾:模型集过小可能无法覆盖目标运动模式,增加模型可以提高精度但计算量增大,且引入过多模型竞争会使算法性能下降,这就要求我们合理选择模型个数来平衡系统的性能。
2 基于STF的UKF自适应算法
STF算法是通过引入渐消因子,根据残差自适应调节增益矩阵,使其能够根据突变特性,动态地调整对于过去时刻观测值的权重,降低跟踪误差。
由于强跟踪滤波器具有较强的关于模型参数失配的鲁棒性和关于突变状态的跟踪能力,且计算复杂度[7]适中。本文将其引入到无迹卡尔曼滤波中,加强对于强机动目标的跟踪能力。
具体算法如下所示:
将式(12)、式(14)、式(15)引入渐消因子λ(k+ 1)进行调节[7]:
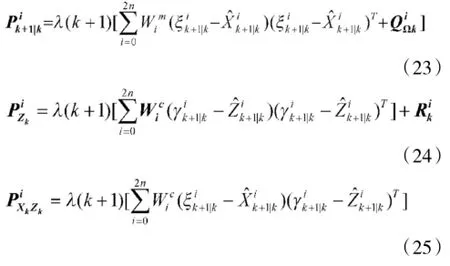
λ(k+1)为加权因子,它的一种次优近似计算方法如下所示:
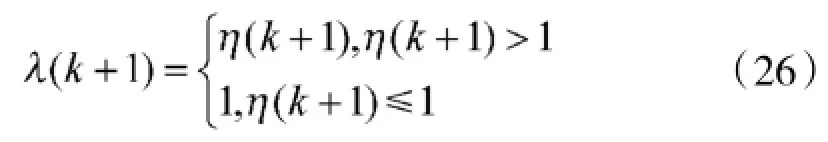
式中各参数的求法分别为:
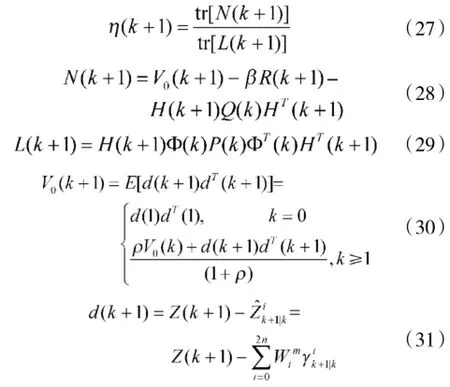
式中:d(k)是残差,d(1)为初始残差;0≤ρ≤1为遗忘因子,一般取ρ=0.95;β为衰减因子,根据经验或仿真设定。
此处通过引入时变的渐消因子,使得输出残差近似正交,使滤波器对模型的不确定性具有更好的鲁棒性,并且强跟踪滤波器自身是收敛的,STF-UKF算法仍然保持了原模型以及自适应算法的收敛性[8]。
3 基于虚拟检测函数法的CS模型参数自适应
“当前”统计模型在估计目标状态的同时还可以估计出机动加速度的均值,实时地修正加速度分布,并通过方差反馈到下一刻的滤波增益中,从而实现闭环的自适应跟踪,具有较好的跟踪效果。本文采用CS模型、CV模型以及CT模型的交互作用,联合对飞行目标进行跟踪。但由于CS模型受最大加速度以及机动频率的限制,致使对于机动目标状态突变时的跟踪效果并不理想。本文提出一种虚拟检测函数方法,通过求新息的均方值与其协方差的比值,并与所选门限比较,根据所得结果调节机动参数,改善模型性能。
虚拟检测函数表达式如下式所示:
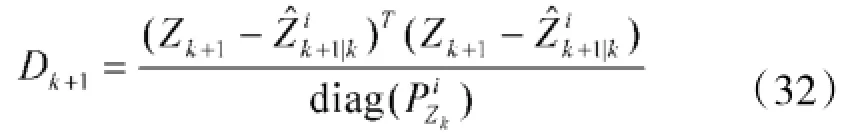
当目标发生弱机动时,分子分母较接近,比值趋向1;当目标发生强机动时,分子上的波动性远大于分母,则比值Dk+1变大。当Dk+1变大的某一定值时,表明目标的机动强度已超过模型所能达到的匹配程度,此时需要迅速调节模型参数以适应目标模式的变化。令Dk+1小于门限ϑ的概率为可接受的虚警概率Pf,Dk+1大于门限ϑ时,可判定目标发生强机动。
3.1判定门限的选取
为了确定合理的判决门限,需要综合考虑两种概率:真实目标未发生强机动却判定其发生强机动的概率:虚警概率Pf;真实目标产生强机动却判定为未发生强机动的概率:漏检概率Pm。提高所选门限,则虚警概率将会降低,漏检概率则会提高;降低门限值,则虚警概率将会提高,漏检概率则会降低,并且门限ϑ的选择还会影响目标检测的实时性,过大的门限会产生较大的机动检测延迟,影响跟踪的实时性。
通过新息的统计特性可知,Dk+1服从自由度(量测维数)为m的χ2分布(自由度为m的χ2分布,均值为m,方差为2m)。应用恒虚警定理,取m=2,Pf=0.15,查表所得门限为ϑ=2.405。
3.2参数自适应算法
①当Dk+1>ϑ时,算法判定为目标发生强机动,此时为了减免CS模型机动参数恒定的缺点,就要通过对虚拟检测函数对机动参数进行调控,调整算法如下:
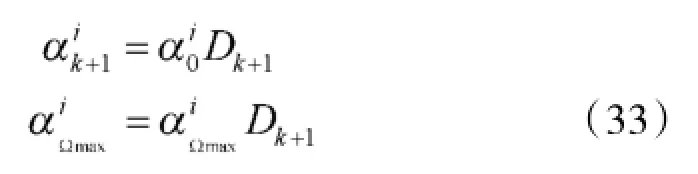
②当Dk+1≤ϑ时,算法判定为目标发生弱机动或是未发生机动,机动参数不作调整。
4 仿真及性能分析
4.1仿真条件
为了验证本文算法的有效性,将本文算法与采用IMM-UKF滤波算法进行比较,在直角坐标系下通过蒙特卡洛方法检验各算法对于机动目标跟踪的性能。目标飞行时间为660 s,采样周期T=1 s,初始状态为X0(0,270,0,15 000,0),机动频率选为1/60,X、Y的轴量测噪声为均值为0,标准差为100 m2的高斯白噪声,机动情况见表1。

表1 目标机动情况
4.2评价指标
实验结果的评价指标采用状态估计质量。状态估计质量取均方根误差(RMSE),定义为:
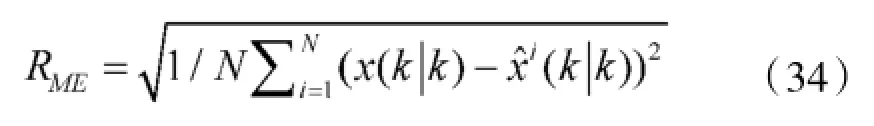
式中,N为Monte Carlo仿真次数,i表示第i次仿真,x(k|k),x^i(k|k)表示第i次运行时k时刻目标状态的真值及总体估计,目标状态在本实验中为目标的位置、速度以及加速度。
4.3仿真结果及分析
本次实验采用20次Monte-Carlo仿真。其结果如图2~图5。
本文采用机动目标运行轨迹为蛇形轨迹,航迹如图2。
图2 目标真实航迹
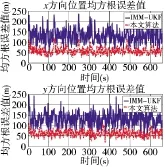
图3 XY位置RMSE对比
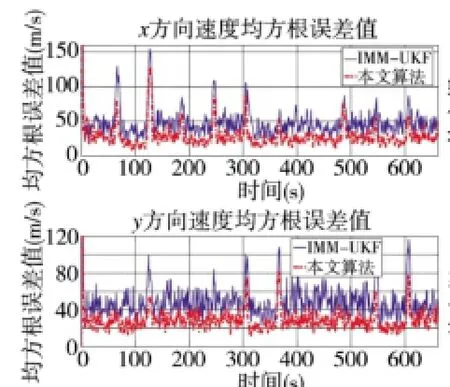
图4 XY速度RMSE对比

图5 XY加速度RMSE对比
由图3~图5可知,本文提出的改进算法在引入强跟踪滤波器和虚拟检测函数后,对于位置、速度及加速度的跟踪精度有了明显的提高,对于加速度突变处,本文改进算法通过引入STF算法,使模型能够快速进行目标真实运动,延时大大小于IMM-UKF滤波算法。
表2显示了标准IMM滤波算法、标准IMM-UKF滤波算法以及本文算法,通过各项指标的对比,可以看出改进算法具有较高的费效比。
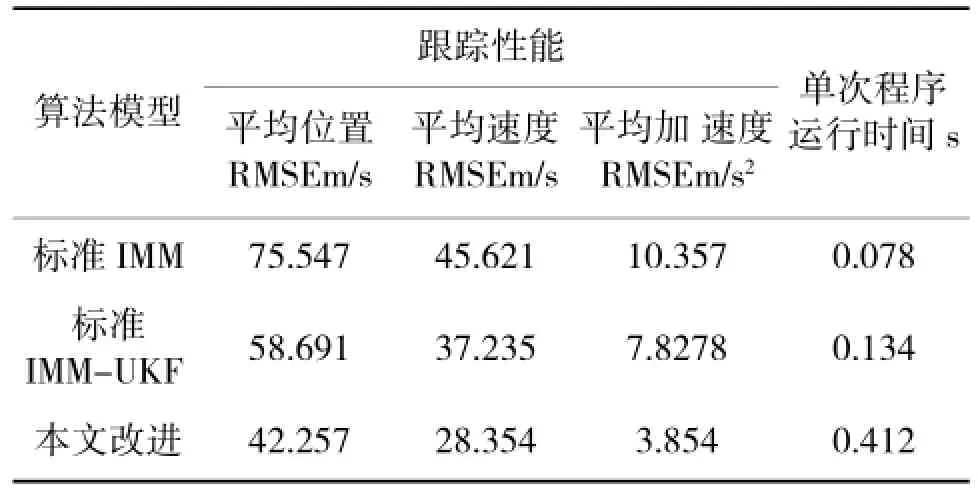
表2 各算法性能比较
5 结束语
本文在基于IMM的结构框架内引入对于非线性滤波性能较好的UKF算法,加强对于强机动目标的跟踪性能,并在UKF算法内加入强跟踪滤波器,对发生机动时刻的新息进行处理,使滤波算法性能更优;提出了基于虚拟检测函数方法,对跟踪中假设的模型参数进行调整,在跟踪过程中更逼近真实目标的运动模式。通过上述仿真对比可以看出,所提方法要优于IMM-UKF滤波算法,显示了算法的有效性和较高的费效比。
[1]Johnston L A,Krishnamurthy V.An Improvement to t-he Interacting Multiple Model(IMM)Algorithm[J].IEEE Trans.-Signal Processing,2001,49(12):2893-2908.
[2]Li X R,Jilkov V P.A Survey of Maneuvering TargetTracking—Part V:Multiple-Model Methods[J].IEEE Trans. Aerospace and Electronic Systems,2005,41(2):18-25.
[3]Mazor E,Averbuch A,Bar-Shalom Y,et al.Interacting Multiple Model Methods in Target Tracking:A Survey[J].IEEE Trans.Aerospace and Electronic Systems,1998,34(1): 103-123.
[4]付昭旺,于雷,刘霞,等.网络信息支持下目标”虚拟跟踪”方法研究[J].电光与控制,2013,20(4):1-6.
[5]刘建书,李人厚,刘云龙.基于”当前”统计模型的交互式多模型算法[J].系统工程与电子技术,2008,30(7): 1351-1354.
[6]范小军,刘锋.一种新的机动目标跟踪的多模型算法[J].电子与信息学报,2007,29(3):532-535.
[7]王满林.自适应衰减记忆UKF算法在三维水下目标跟踪中的应用[J].四川兵工学报,2012,33(5):44-47.
[8]李劲.强跟踪Unscented滤波器及其在无源跟踪中的应用[J].电讯技术,2005(1):160-164.
[9]范小军,刘锋,秦勇,等.基于STF的“当前”统计模型及自适应跟踪算法[J].电子学报,2006,34(6):981-984.
Based on Virtual Detection Function of IMM-UKF Maneuvering Target Tracking
XU Yang,XU Song-tao,LUO Wen-tao,XIANG Jian-jun,QIN Zhan-shi
(Aeronautics and Astronautics Engineering College,Air Force Engineering University,Xi’an 710038,China)
To improve the tracking effect of the maneuvering targets effectively,the Unscented Kalman Filter(UKF)is introduced into the framework of the Interacting Multiple Model(IMM)algorithm,enhancing the precision of state estimation.The Strong Tracking Filter(STF)to the UKF algorithm is applied to avoid the disadvantage of long-time delay and poor performance in the tracking of the strong maneuvering.The virtual detection function is proposed to make the maneuvering parameters of CS model adaptively adjust in the tracking process,which increases the probability of matching rate with the real object model.The simulation results verify the effectiveness of the improved algorithm.
unscented kalman filter,IMM,STF,virtual detection function,maneuvering parameters
TN955.3
A
1002-0640(2015)01-0037-05
2013-12-05
2014-02-07
陕西省电子信息系统综合集成重点实验室基金资助项目(201107Y03)
徐洋(1989-),男,吉林吉林人,硕士研究生。研究方向:目标跟踪与信息融合。
