基于工况-时间分布规律确定装备预防性维修间隔期*

杨智，李金寿，董华玉

（镇江船艇学院，江苏镇江212003）

基于工况-时间分布规律确定装备预防性维修间隔期*

杨智，李金寿，董华玉

（镇江船艇学院，江苏镇江212003）

考虑到装备工况变化通常会影响到装备寿命，提出了一种基于工况-时间分布规律的装备可靠性评估及预防性维修间隔期的确定方法。采用Gamma过程描述装备性能指标退化过程，以形状参数反映工况的变化，推导出基于工况-时间分布规律的装备寿命分布；进而得到可靠度表达式，确定了预防性维修间隔期；最后给出了方法在某6300型柴油机中的应用实例，验证了方法的有效性。

工况-时间分布规律，Gamma过程，预防性维修间隔期，可靠性

0 引言

随着使用时间的延长，装备的性能指标通常会逐渐恶化，比如磨损加剧、运动副间隙扩大、参数漂移量增大、老化等。这种恶化一般是随机的，难以用确定的函数表达式进行描述，数学上常称此过程为退化过程。对于性能指标具有退化趋势的装备，为降低故障的发生概率，通常采取预防性维修方式。预防性维修间隔期是指两次预防性维修之间的工作间隔时间［1］，通常依据安全性、任务性或经济性要求确定。这方面已有很多的理论成果［2-5］，但在这些研究中，通常不涉及装备工况的变化。在实践中，对于同类装备一般也只会给定一个预防性维修间隔期，不涉及工况的变化。而显而易见的是，当装备工况发生变化，会对装备性能指标的退化产生影响，进而影响到装备寿命。如同型号柴油机在工况-时间分布规律有较大差异的巡逻艇和油船上，寿命会有较大差异，预防性维修间隔期不应该统一给定。

所以，一种比较好的情况是由装备使用者根据工况-时间分布规律确定预防性维修间隔期。要实现这一目标，最直接的思路莫过于预先给定装备工况-时间分布规律，进而通过大量试验得到该分布规律下的寿命分布。然而，此方法只能对经验的、最常见的工况分布进行模拟，装备使用者不能根据实际的工况-时间分布规律要求提前或延长维修间隔期。而另一条可能的途径是对变工况下的装备性能指标退化过程进行建模分析，进而确定预防性维修间隔期，我们的着力点正在于此。

对于变工况下的退化过程描述，大都以Gamma过程作为研究的载体，其中的原因是Gamma过程增量具有独立性和非负性，符合退化过程的要求［6-9］。文献［10-11］将退化过程分成两种模式：正常和加速模式，并分别用平稳Gamma过程进行描述。在文献［10］中，模式的变化时间是随机的，服从一个给定的分布；在文献［11］中，模式的变化时间需要利用算法进行探测。日本学者Tsaing针对现有可靠性加速寿命试验的不足，提出了一种在试验中逐渐增加载荷的方法，称之为逐级加压加速寿命试验［12］，然后用Gamma过程对各压力下的退化进行描述［14］，并以平均寿命的标准差最小为目标，对试验的产品数目、各压力的施加时间等进行了优化设计。上述文献中提到的模式、压力可与这里的工况类比，但这里的工况-时间分布规律是给定的，既不是随机的，也不是一个优化的目标。

1 基于工况-时间分布规律的装备寿命分布

Gamma过程{X（t），t≥0}满足［7］：

（1）具有独立增量；

（2）对任意t＞s≥0，增量X（t）-X（s）～Ga（a（t）-a（s），b）；

（3）X（0）=0。

其中，Ga（·）表示Gamma分布，a（t）和b分别为形状参数和尺度参数，且a（t）（t≥0）为递增连续函数，a（0）=0，b＞0。当a（t）为线性函数时，Gamma过程为平稳过程，a（t）为非线性函数时为非平稳过程，这里采用平稳Gamma过程。

设a（t）=ait，∀i=1，…，m，m为总的工况数。ai随工况i的改变而改变，可设想在规定的工况下对装备性能指标退化分别进行试验，利用极大似然法或矩法确定；不同工况下b保持不变，为常数，可简单假设为1。

假设某装备在时间T内采用了m种工况，各工况分别对应的叠加时间为t1，t2，…，tm，占总时间T的百分数为p1，p2，…，pm，则有：

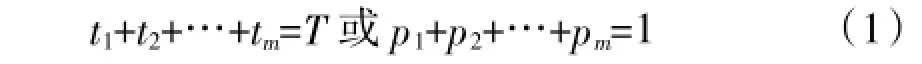
t1，t2，…，tm或p1，p2，…，pm可按经验、要求或装备配置的工况-时间分布记录装置给定。比如：100%最大功率的使用时间占到使用期的10%，80%最大功率的使用时间占到使用期的50%，60%最大功率的使用时间占到使用期的20%，小于20%最大功率的使用时间占到使用期的20%。

T时间内总的退化量：

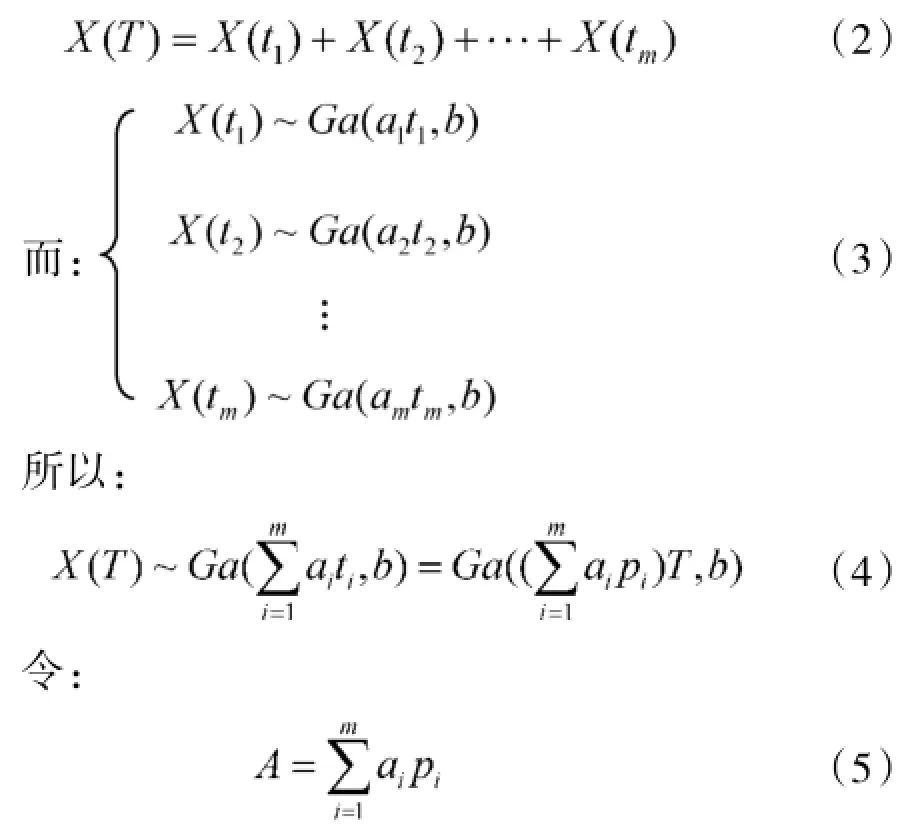
定义其为叠加工况参数。有X（T）～Ga（AT，b），即：

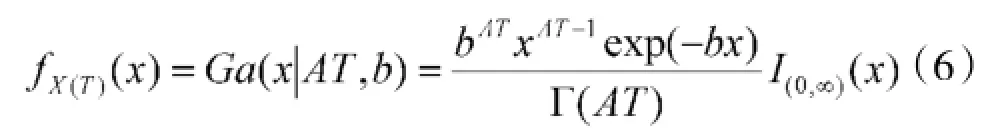
其中，Г（·）表示Gamma函数；I（x）=1，x∈（0，∞）。其形式与标准的平稳Gamma过程完全一致。当将各工况参数ai对应的使用时间百分数pi看成概率时，由式（5），A可视为工况参数分布概率，如表1所示。

表1 工况参数分布

由式（6）有：

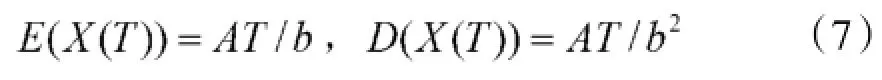
假设该装备性能指标退化阈值为ymax，则寿命分布为：

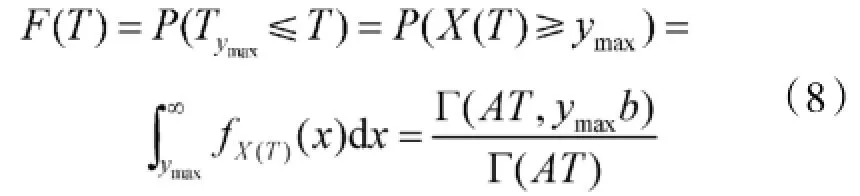
T时刻的可靠度：

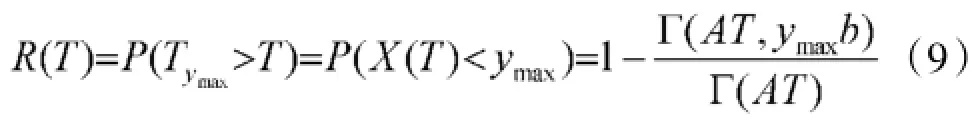
T时刻的故障率：

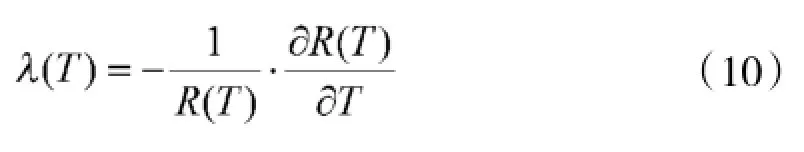
对于式（9）～式（10）的计算，可在Maple或Matlab等软件上进行。当工况-时间分布规律根据实际情况或按照装备使用者的要求发生变化时，由式（5）计算新的A值，再代入式（8）～式（10），即可得新的寿命分布、可靠度或者故障率值。

在此基础上，可确定装备预防性维修间隔期。以定期维修间隔期的确定为例，对此进行一些讨论。类似的讨论也可延伸到其他预防性维修工作类型的确定中去，如功能检测间隔期、使用检查间隔期的确定等。

2 定期维修间隔期的确定

2.1 按安全性要求确定间隔期

（1）按照给定的可靠度确定间隔期

由式（9），绘制R（T）～T曲线，给定可靠度水平（如0.95）对应的时间T即为定期维修间隔期；

（2）按照给定的故障率确定间隔期

由式（10），绘制λ（T）～T曲线，给定故障率水平（如0.01）对应的时间T即为定期维修间隔期。因A＞0，此寿命分布的故障率是递增的［15］，所以与可靠度曲线一样，其对应的值是唯一的。

2.2 按任务性要求确定间隔期

假设该装备已按一定的工况-时间分布规律工作到T时间，如要求再在某工况ai下工作一段时间ΔT的任务可靠度为一给定值，可按下述方法确定定时维修间隔期。此时任务可靠度为：

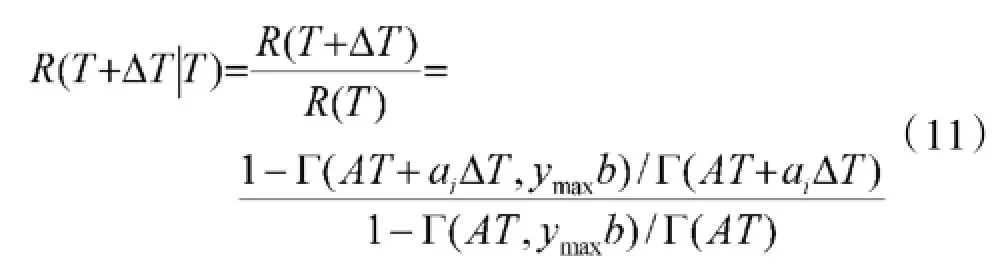
因ΔT、ai给定，可绘制R（T+ΔT|T）～T曲线，给定任务可靠度水平（如0.95）对应的时间T即为定期维修间隔期。

2.3 按经济性要求确定间隔期

间隔期T内单位工作时间总费用［1］：

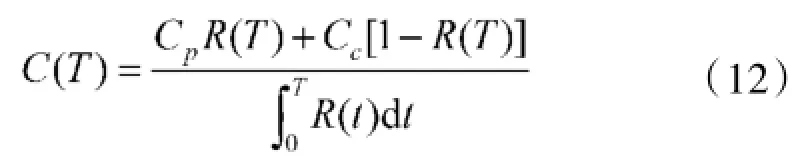
其中：Cp表示定期维修费用，Cc表示故障后维修费用；可靠度R（t）、R（T）表达式可由式（9）得到。通过绘制C（T）～T曲线，C（T）最小值对应的T值即为要求的定期更换间隔期。

3 应用实例

某工作型船舶上使用的6300型柴油机气缸套内圆表面磨损极限为1mm（气缸套是易损件，通常由其决定柴油机的大修期。为简单起见，忽略气缸套其他损伤形式）。预估的工况-时间分布规律如表2所示，参数b为1。现需考察：

（1）该柴油机8 kh时的可靠度；

（2）以故障率达到0.02为指标确定该柴油机大修期；

（3）当实际的工况-时间分布规律与预估的不同时（大功率的使用时间占总时间比值显著变大，见表2），回答问题（1）、（2）。

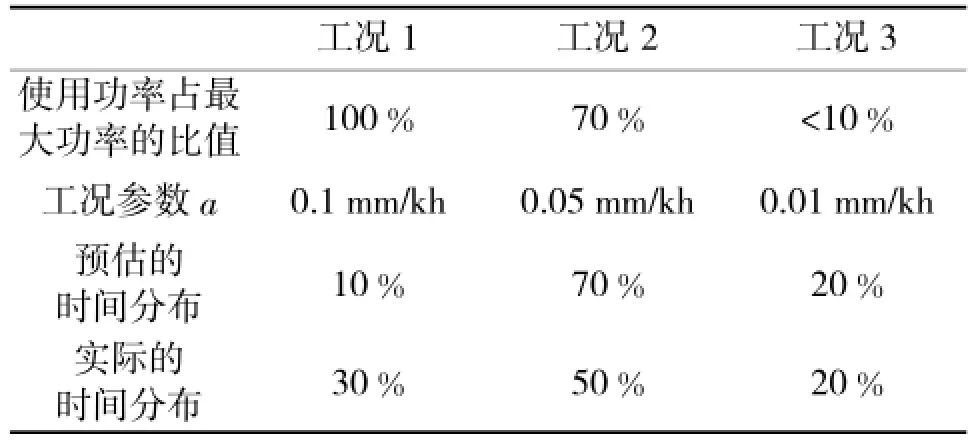
表2 该柴油机预估及实际的工况-时间分布规律

按照前面思路：

问题（1）：由表2及式（5）：A=0.047；又b=1，ymax=1 mm。由式（9）绘制R（T）～T曲线如图1曲线1所示，可见，8 kh的可靠度为0.89。

问题（2）：由式（10）绘制λ（T）～T曲线如图2曲线1所示。可见，故障率为0.02时，大修期为9 kh。

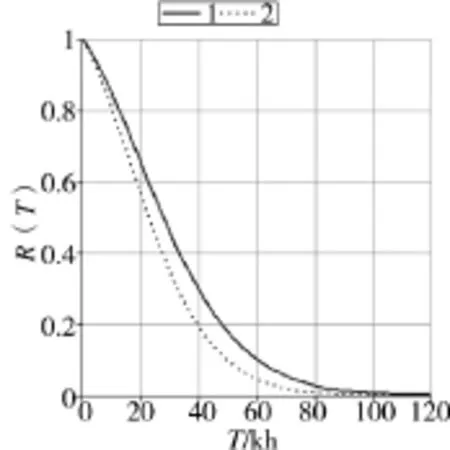
图1 R（T）～T曲线

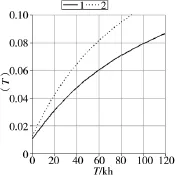
图2 λ（T）～T曲线

问题（3）：由表2及式（5）：A=0.057。绘制R（T）～T曲线、λ（T）～T曲线分别如图1、图2中曲线2所示。可见，8 kh的可靠度为0.85；故障率为0.02时，大修期为4 kh。即当大功率的使用时间占总时间比值变大时，可靠度降低，大修期大幅度缩短，与实际情况相符。

4 结束语

预防性维修间隔期的确定是装备维修决策中的一个重要问题，研究成果已见诸多种维修理论书籍及文献。但在这些研究中，通常不涉及装备工况的变化。为此，本文基于可靠性及Gamma随机过程理论，对此问题进行了初步研究，最终达到了由装备使用者根据工况-时间分布规律，确定预防性维修间隔期的目的。

［1］陈学楚.现代维修理论［M］.北京：国防工业出版社，2003：125-151.

［2］Wu S M，Zuo M J.Linear and Nonlinear Preventive MaintenanceModels［J］.IEEETransReliab，2010，59（1）:242-249.

［3］GhasemiA，YacoutS，Ouali M S.Parameter Estimation Methods for Condition-Based Maintenance with Indirect Observations［J］.IEEE Trans Reliab，2010，59（2）:426-439.

［4］曾杰，董俊杰.基于可靠性重要度的复杂产品定时维修间隔期优化［J］.装备学院学报，2013（2）：108-111.

［5］腾红智，殷军辉，李锋，等.基于模糊决策的预防性维修间隔期评判方法［J］.火力与指挥控制，2011，36（3）：177-179.

［6］Abdel H M.A Gamma Wear Process［J］.IEEE Trans Reliab，1975，24（2）:152-153.

［7］NoortwijkJM.ASurveyoftheApplicationofGammaProcesses in Maintenance［J］.Reliab Eng Syst Safety，2009（94）：2-21.

［8］Kyung S P.Optimal Wear-Limit Replacement with Wear-Dependent Failures［J］.IEEE Trans Reliab，1988，37（3）: 293-294.

［9］Esary J，Marshall A，Proschan F.Shock Models and Wear Processes［J］.Annals of Probability，1973，1（4）:627-649.

［10］Saassouh B，Dieulle L，Grall A.Online MainteNance Policy for a Deteriorating System with Random Change of Mode［J］.Reliab Eng Syst Safety，2007（92）：1677-1685.

［11］Fouladirad M，Grall A，Dieulle L.On the use of on-line Detection for Maintenance of Gradually Deteriorating Systems［J］.Reliab Eng Syst Safety，2008（93）：1814-1820.

［12］Tseng S T，Wen Z C.Step-stress Accelerated Degradation Analysis of Highly-reliable Products［J］.Journal of Quality Technology，2000（32）:209-216.

［13］郭齐胜，李智国，张迪，等.基于任务分析的维修力量数量预测方法［J］.四川兵工学报，2014，35（1）:5-9.

［14］Tseng S T，Balakrishnan N，Tsai C C.Optimal Step-stress Accelerated Degradation Test Plan for Gamma Degradation Processes［J］.IEEE Trans Reliab，2009，58（4）:611-618.

［15］Liao H，Elsayed E A，Chan L Y.Maintenance of Continuously Monitored Degrading Systems［J］.Eur J Oper Res，2006，175（2）:821-835.

Determine Interval of Preventive Maintenance of Equipment Based on Running State-time Distributing

YANG Zhi，LI Jin-shou，DONG Hua-yu
（在henjiang Watercraft College，在henjiang 212003，China）

Considering a change of Running State often effects life of an equipment，a reliability assessment and interval of Preventive Maintenance determine method for the equipment based on Running State-time distributing is proposed.A gamma process is employed to describe a degradation process of the equipment performance，and the change of running state is reflected by shape parameter，the life distribution of the equipment is derived based on Running State-time distributing.Then an expression of reliability is obtained and the interval of Preventive Maintenance is determined.Finally an apply case in a 6300 type diesel engine is given，which demonstrated the validity of the method.

running state-time distributing，gamma process，interval of preventive maintenance，reliability

TB114.3

A

1002-0640（2015）01-0034-03

2013-10-25

2014-02-28

军队科研基金资助项目（××［2009］83号）

杨智（1978-），男，湖南娄底人，博士。研究方向：装备可靠性及维修决策。