五法解一道高考选做题

刘佑威

（江西省信丰中学）

（1）求实数a，b的值；

（

（2015年高考陕西卷文理科数学选做题第24题）

注 第（1）题中容易求得a=-3，b=1，具体过程略；本文就第（2）题关于t的无理函数最大值的求解进行探究.

解法1（柯西不等式法）

解法2（构造向量法）

解法3（三角换元法）

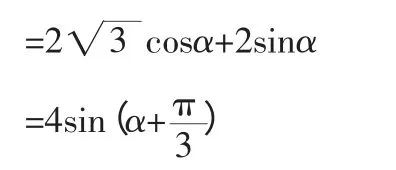
解法4（代数换元法）

易知u2+3v2=12.

其可行域为椭圆u2+3v2=12在第一象限的部分，沿初始直线u+v=0往上平移，z的值越来越大；当平移至与椭圆在第一象限的部分相切时，z达到最大值，此时的切点为最优解.容易求得相切时的切点坐标为（3,1），∴zmax=3+1=4.

故（■ - 3t+12+ ■ t ）max=4.

解法5（求导法）

不妨设（ft）= ■- 3t+12+ ■ t ，t∈［0， 4］.

令f（＇t）=0，解得t=1.

由f（＇t）＞0，解得0≤t＜1；

由f（＇t）＜0，解得1＜t≤4.

则函数（ft）在［0， 1］上递增，在［1， 4］上递减，

∴函数f（t）在t=1取得极大值，同时也取得最大值，