基于等效静态载荷理论的机床运动部件轻量化设计

段朋云,　丁晓红

(1.上海理工大学 公共实验中心,上海　200093;2.上海理工大学 机械工程学院,上海　200093)



基于等效静态载荷理论的机床运动部件轻量化设计

段朋云1,丁晓红2

(1.上海理工大学 公共实验中心,上海200093;2.上海理工大学 机械工程学院,上海200093)

摘要：为保证机床的加工精度和切削效率,机床的运动部件需要较高的刚度和较轻的质量.以某型号磨床的主轴箱为研究对象,建立包含主轴箱、电主轴磨头和滚珠丝杠等部件的有限元柔性多体动力学模型,运用等效静态载荷理论将柔性多体动力学分析与静态结构优化理论相结合,采用拓扑优化技术对主轴箱进行轻量化设计.与传统静态载荷下的主轴箱结构拓扑优化设计相比,该方法更适用于机床运动部件的结构轻量化设计,优化后的主轴箱结构在保证静动态性能的前提下质量减轻8.5%.

关键词：机床运动部件; 等效静态载荷; 轻量化; 结构拓扑优化

主轴箱是高速高精密机床的关键部件,主要用于安装机床主轴及其传动部件,要求其具有较高的刚度以保证加工精度,同时能够实现高速进给、快速换向和稳定切削.这就要求在切削运动中快速移动的主轴箱有较轻的质量,以减少运动惯性和变形,因此在满足刚度的条件下对主轴箱进行轻量化设计具有重要意义.

韩江等[1]通过有限元软件建立了主轴箱的有限元计算模型,并对其进行静动态特性分析,结果表明,主轴箱的刚度和强度较好,一阶固有频率较低,对主轴箱结构的改进设计具有一定的指导意义.丛明等[2]通过引入待优化模型的邻接零件,建立了某型号主轴箱及相关部件的装配体模型,使得边界条件更加逼近实际情况,并应用叠加原理处理了机床产品结构优化设计中载荷种类多的问题,经过拓扑优化得到的新设计模型动静态性能都能很好地满足设计要求.陆君等[3]基于有限元方法先对主轴箱箱体毛坯进行了宏观结构的拓扑优化,结合工艺要求建立初步模型,进行敏感度分析,对主轴箱参数进行更有效的设计,最大程度地提高了箱体的刚度.牛颖等[4]利用有限元软件对主轴箱进行了静力分析和模态分析,在此基础上对主轴箱进行了多目标尺寸优化设计,优化后的主轴箱重量降低,刚度提高.目前主轴箱的轻量化设计多数是在静态载荷情况下进行的,但工作中的主轴箱实际受到动载荷作用[5-6].由于动载荷在优化过程中往往难以直接施加,导致因载荷条件不准确而使设计结果不是最优.近年发展起来的基于等效静态载荷理论的优化方法,将动态载荷优化问题转化成静态载荷优化,应用静态结构优化的成熟技术进行求解[7-8].这一方法已成功应用于柔性多体系统的部件结构优化中,并呈现出一定的优势[9-13].本文以某型号机床的主轴箱为研究对象,提出一种基于等效静态载荷理论的机床运动部件轻量化设计方法,通过与原始设计方案及静态拓扑优化设计结果进行比较,说明基于等效静态载荷理论的动态结构优化方法在机床运动部件结构优化设计中的可行性和有效性.

1基于等效静态载荷理论的主轴箱结构拓扑优化

1.1等效静态载荷理论简介

当结构承受动态载荷时,在某一时刻,结构会发生变形,从而产生一个位移场.如果在这一时刻存在一个静态载荷作用于结构之上,该载荷产生与动态载荷作用下相同的位移场,那么称该静态载荷为这一动态载荷在某一时刻的等效静态载荷[7,12].一般地,不考虑阻尼,动态载荷作用下结构的运动方程为

(1)

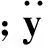
(2)

或

(3)

式中,feq为t时刻的等效静态载荷,即

(4)

由式(4)可以看出,等效静态载荷由外力和结构的惯性力求出,且只有对结构进行瞬态分析之后才能计算得到.

由于在离散的时域中可求解式(1),因此在离散的时域内也可以求解等效静态载荷.在i时刻,等效静态载荷可以在进行柔性多体动力学瞬态分析后求得,即

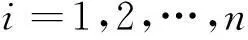
(5)

式中,n为瞬态分析中所截取的时间点个数,即等效静态载荷数目.

1.2优化方法流程与步骤

图1为瞬态振动系统运用等效静态载荷进行优化的流程,其算法步骤如下:

步骤1赋初值,令p=0,xp=x0,p为迭代次数,

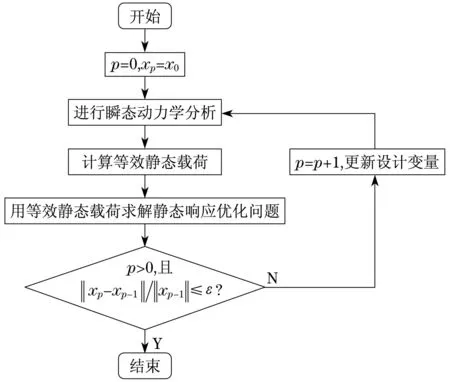
图1　基于等效静态载荷法的结构优化流程[8]

x为设计变量.

步骤2将第p次迭代的结果xp代入式(1)进行瞬态振动分析.

步骤3用式(5)计算所有时间步的等效静态载荷集.

步骤4使用计算所得的等效静态载荷求解线性静态响应优化问题:

(6)

式中:x为设计变量;φ为目标函数;feq为等效静态载荷;gj为第j个约束函数;n为瞬态分析中所截取的时间点数;m为约束个数.优化过程中载荷工况的数目与离散时间域中时间步的数目相同.

步骤5当p=0,转到步骤6.

当p>0,如果‖xp-xp-1‖/‖xp-1‖≤ε,优化终止;否则,转到步骤6.xp是第p次迭代时的设计变量,ε是一个极小的数.

步骤6令p=p+1,转到步骤2.

2基于等效静态载荷理论的主轴箱结构拓扑优化

2.1主轴箱部件的刚柔耦合多体动力学仿真分析

目前,只有对系统进行瞬态振动分析才能得到等效静态载荷,因此,对于选定的优化部件,首先可通过系统瞬态振动分析计算得到等效静态载荷,进而用于结构优化.本文以某高速高精密数控机床的主轴箱为例来进行说明.该主轴箱由滚珠丝杠副驱动在机床的溜板上作往复直线运动,最大行程为1 000 mm,快速移动速度为40 m/min,移动加速度为5 m/s2.首先建立主轴箱部件构成的实体模型,如图2所示.该模型主要由主轴箱、丝杠、电主轴磨头3大部分组成.4个滑块通过螺栓连接固定在主轴箱上,丝杠螺母通过轴承固定于主轴箱上,并同时与丝杠构成丝杠螺母副.丝杠由其顶部电机驱动旋转,带动主轴箱与丝杠螺母在4个滑块的导向作用下沿Z方向来回快速移动.电主轴磨头通过轴承固定在主轴箱通孔中,主轴箱承载着电主轴磨头到达指定切削位置完成切削加工.根据上述装配关系,丝杠顶部建立旋转副,螺母及4个滑块中心处建立移动副,电主轴磨头与主轴箱之间用固定副模拟.根据计算多体系统动力学的相关知识,将主轴箱视为柔性体处理,其他部件作刚体处理.主轴箱部件的多体系统有限元模型如图3所示.

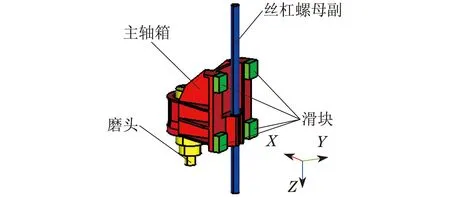
图2　主轴箱部件实体模型

图3　主轴箱部件多体系统有限元模型

当主轴箱沿Z轴反方向加速移动时,受到的惯性力作用方向与重力方向一致,此时主轴箱受力情况最恶劣.根据主轴箱部件的运动规律,对丝杠螺母副处的移动副施加位移驱动,使主轴箱完成沿Z轴反方向加速→匀速→减速运动的过程,位移驱动曲线如图4(a)所示(见下页),相对应的速度曲线如图4(b)所示(见下页).

主轴箱部件的运动周期为1.56 s,对其多体动力学的仿真参数进行设定,取仿真步长为0.01 s,则该运动时间在时间域内被离散成156个时间点.在每个时间点进行等效静态载荷计算，得到主轴箱柔性体的加速度变化曲线,如图5(a)所示(见下页),主轴箱柔性体应力最大单元的应力变化曲线如图5(b)所示(见下页).其他单元的应力变化情况与此曲线趋势相同,但不同单元的应力大小不同.

主轴箱的最大加速度为5 m/s2,由主轴箱的加速度变化曲线图5(a)可知,因主轴箱运动方向沿Z轴反方向,故在其刚开始运动时加速度有剧烈的变化；当主轴箱将要达到最大速度时,加速度出现了一定的波动,绝对值最大,这是由加速运动往匀速运动变化所致.同样,在匀速运动向减速运动过渡时,加速度同样出现波动.从主轴箱应力最大单元的应力曲线图可知,第0.01 s时,主轴箱从静止到加速运动,相当于突然施加了一个较大的惯性力,故最大应力激增.第0.13 s时,也就是主轴箱的速度将要达到最大移动速度时,最大应力有个突变,达到2.72 MPa,这是应力最大单元在主轴箱运动时间域内达到的应力最大值.从第1.42 s起到运动结束这段时间,主轴箱作减速运动,开始减速时应力也发生了突变,因为这相当于给主轴箱施加了一定的惯性力,加之主轴箱已经到达溜板的最上部,使得应力最大单元这段时间内的应力值也较大.总之,加速度变化曲线与应力最大单元的应力变化曲线基本一致,在同样的切削力外部载荷作用下,某些时刻由于突然增加了惯性力,导致应力最大单元的应力相应地发生了变化.

图4　主轴箱位移驱动曲线与相对应的速度曲线

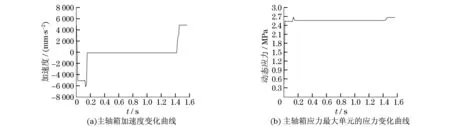
图5　主轴箱柔性多体动力学仿真分析结果

2.2基于等效静态载荷理论的主轴箱结构拓扑优化设计

2.2.1定义主轴箱初始优化空间

为了提高结构的刚度,原型方案设置了4组加强筋板,如图6所示.为了对主轴箱上的筋板进行重新布置,需将原有筋板的区域填补,获得优化空间,如图7所示.主轴箱初始优化模型被分为设计区域和非设计区域两部分.设计区域即为拓扑优化空间,根据主轴箱在拓扑优化时制造约束的不同,将设计空间分为两个区域.非设计区域为模型中与约束及载荷作用相关联的实体单元和箱体内部不受载荷作用的支撑板等区域.主轴箱的通孔部分需放置电主轴磨头等部件,为非设计区域；另外与滚珠丝杠螺母副与滑块装配的部分也为非设计区域.

2.2.2优化数学模型

优化的数学模型包括设计变量、目标函数与约束条件,并根据设计要求有所不同.主轴箱既需要较好的动静态性能,又需要尽可能轻的质量,由此建立优化数学模型为

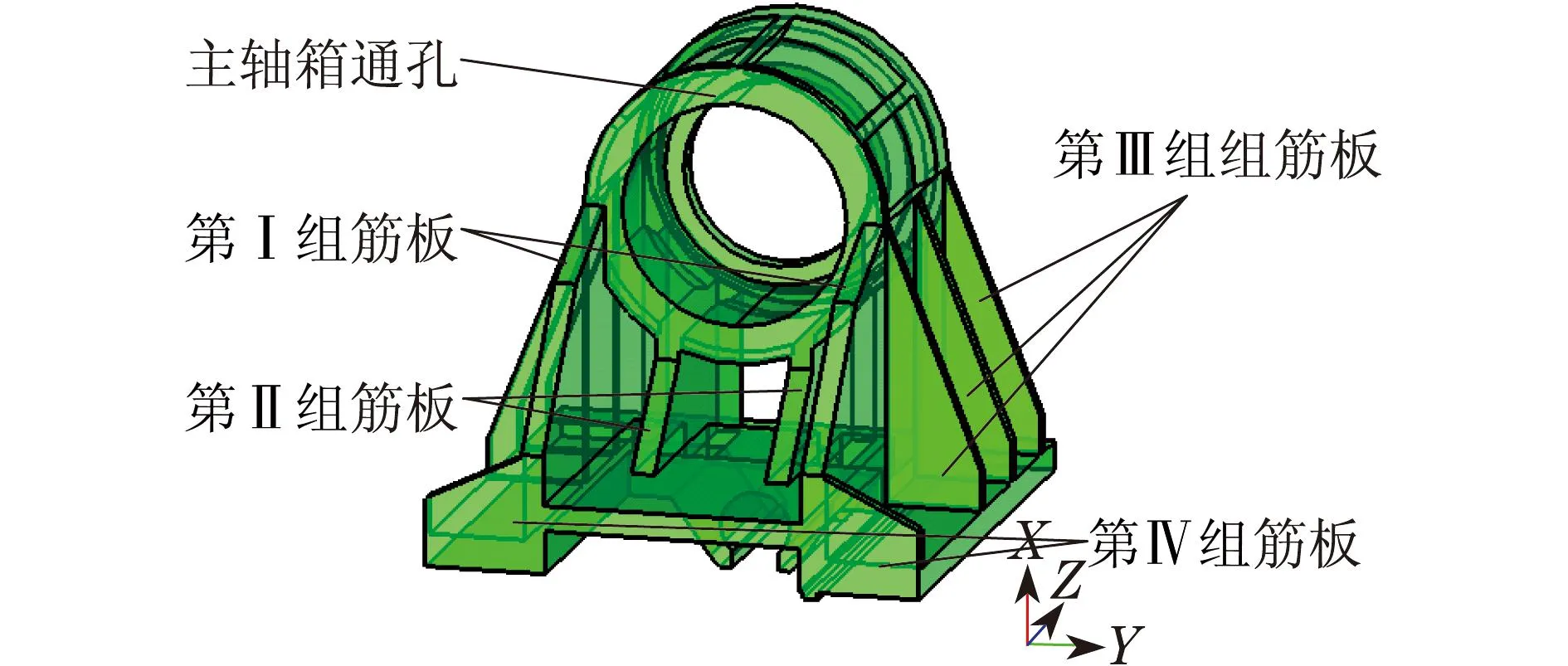
图6　主轴箱原始模型

图7　主轴箱初始优化实体模型

(7)

式中:X为单元密度向量;xi为第i个单元密度;Umax为主轴箱运动过程中的最大应变能;Vf为体积分数,体积分数的计算公式为

(8)

式中:Vc为当前迭代的总体积;Vo为初始非设计区域体积;Vi为初始设计体积.

2.2.3优化设计结果

经过循环迭代得到的主轴箱拓扑形态如图8(a)所示,根据优化结果新设计的方案如图8(b)所示.去除了原始设计方案中的第I组筋板与第II组筋板,在第II组筋板位置处布置了Y型交叉筋板,此为新设计方案的第I组筋板.原始设计方案的第III组筋板只保留了两块通孔底部处的加强筋,两块加强筋之间新布置了筋板,并开了窗口,此为新设计方案的第II组筋板.原始设计方案的第IV组加强筋形态与位置有所改变,在第IV组加强筋与通孔上部之间新布置了筋板,此为新设计方案的第III组筋板.

图8　基于等效静态载荷理论的主轴箱优化结果

3主轴箱静态拓扑优化

3.1主轴箱静动态性能分析

为了说明等效静态载荷方法在机床运动部件结构优化设计中的有效性及优越性,采用传统静态载荷下的结构拓扑优化设计技术对主轴箱进行静态拓扑优化设计.对主轴箱进行静态拓扑优化时,首先要对主轴箱原始设计方案进行静动态性能分析[14],主轴箱部件动静态性能分析的边界条件如图9所示.在主轴箱上的4个滑块与主轴箱一起沿溜板箱上的导轨做Z轴方向的快速移动,故约束4个滑块表面X向与Y向的平动自由度.丝杠两端固定在溜板上,故约束丝杠两端的6个自由度.主轴箱所受的载荷条件主要有两部分组成,一部分是主轴箱自重及安装在上面的部件的重力作用,一部分是来自电主轴磨头在磨削过程中产生的磨削力,磨削力主要为沿Y轴方向的切向磨削力Fy和沿X轴方向的径向磨削力Fx.主轴箱原模型动静态性能分析结果为切削点变形0.018 mm,整体应变能大小约为46.6 J,一阶固有频率为202.7 Hz.

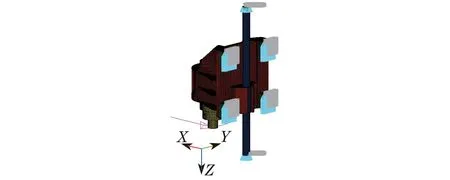
图9　主轴箱原始设计方案的有限元模型

3.2主轴箱静态拓扑优化设计

主轴箱静态拓扑优化的初始优化模型与基于等效静态载荷理论的主轴箱初始优化模型相同,优化数学模型为

(9)

式中,Utotal为主轴箱部件的整体应变能.

主轴箱静态拓扑优化结果如图10所示.静态拓扑优化新设计方案保留了原始设计方案的第I组筋板,去除了原始设计方案的第II组筋板.在通孔底部新布置了开有窗口的筋板,此为新设计方案的第II组筋板.新设计方案去除了原始设计方案第III组筋板的前两块筋板,保留了靠近通孔底部的两块筋板,此为新设计方案的第III组筋板.新设计方案的第IV组筋板与原始设计方案的第IV组筋板相似.

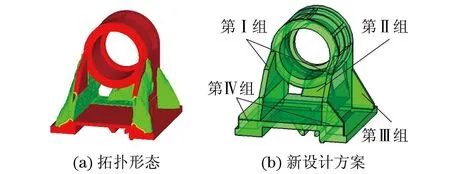
图10　主轴箱静态拓扑优化结果

4优化前后设计方案的性能对比

分别对基于等效静态载荷理论拓扑优化新设计方案与静态拓扑优化新设计方案进行动静性能分析,从模型重量、切削点的变形δ、主轴箱部件整体应变能Utotal和一阶固有频率f1对优化前后的设计方案进行评价,两种新设计方案与原始设计方案的对比如表1所示.

表1　优化前后主轴箱结构性能比较

由表1可知,主轴箱原始设计方案具有较好的动静态性能,而筋板布置型式存在一定的缺陷,设计趋于保守.基于等效静态载荷理论的主轴箱结构拓扑优化新设计方案与原设计方案相比减重8.5%,而切削点变形及应变能与原有设计方案基本相同.另外,新设计方案的一阶固有频率较原有设计方案仅降低1%,影响很小.这说明基于等效静态载荷理论的结构拓扑优化方法在机床部件结构优化中具有较好的适用性和有效性.在同样的优化数学模型下,主轴箱静态拓扑优化设计方案与原方案相比减重7%,动静态性能基本保持不变.就主轴箱两种新设计方案而言,基于等效静态载荷理论的结构拓扑优化方法比静态拓扑优化方法更具优势,前者结合移动部件的特点,不仅考虑移动部件在切削加工时的性能,还考虑了移动部件进给时候的性能;在减重方面,前者比后者效果要好,因为移动部件为了降低快速移动时的惯性力与空转时的功耗等,要求更轻质量的部件结构.

5结论

采用基于等效静态载荷理论的结构拓扑优化方法对快速移动的主轴箱进行轻量化设计,研究表明,对于运动部件,相比静态拓扑优化方法,基于等效静态载荷理论的结构拓扑优化方法在满足结构性能要求的前提下,减重效果更好.研究结果可为其他运动部件如溜板箱、工作台的结构设计提供参考.

参考文献：

[1]韩江,孟超,姚银鸽,等.大型数控落地镗铣床主轴箱的有限元分析[J].组合机床与自动化加工技术,2009(10):82-84.

[2]丛明,宋健,王贵飞,等.高速卧式加工中心主轴箱拓扑优化设计[J].组合机床与自动化加工技术,2011(9):18-21.

[3]陆君,文怀兴.高速立式加工中心主轴箱敏感度分析及优化[J].组合机床与自动化加工技术,2010(8):1-2.

[4]牛颖,李全普,于俊光.HDBS-63高速卧式加工中心主轴箱多目标优化设计[J].组合机床与自动化加工技术,2011(6):77-80.

[5]周孜亮,王贵飞,丛明.基于ANSYS Workbench的主轴箱有限元分析及优化设计[J].组合机床与自动化加工技术,2012(3):17-20.

[6]陈庆堂.基于ANSYS的数控铣床主轴箱优化设计[J].莆田学院学报,2005,12(5):72-74.

[7]Kang B S,Choi W S,Park G J.Structural optimization under equivalent static loads transformed from dynamic loads based on displacement[J].Computers and Structures,2001,79(2):145-154.

[8]Choi W S,Park G J.Structural optimization using equivalent static loads at all time intervals[J].Computer Methods in Applied Mechanics and Engineering,2002,191(19/20):2105-2122.

[9]Kang B S,Arora J,Park G J.Optimization of flexible multibody dynamic systems using the equivalent static load method[J].AIAA Journal,2005,43(4):846-852.

[10]Hong E P,You B J,Kim C H,et al.Optimization of flexible components of multibody systems via equivalent static loads[J].Structural and Multidisciplinary Optimization,2010,40:549-562.

[11]Park G J.Technical overview of the equivalent static loads method for non-linear static response structural optimization[J].Structural and Multidisciplinary Optimization,2011,43(3):319-337.

[12]赵礼辉.ESL法在汽车结构优化设计中的应用[D].上海:上海交通大学,2009.

[13]杨志军.基于等效静态载荷原理的高速机构结构拓扑优化方法[J].机械工程学报,2011,47(17):119-126.

[14]关瑞臣,李郝林.平整机牌坊有限元分析[J].上海理工大学学报,2013,35(6):603-606.

(编辑:丁红艺)

第一作者： 麦云飞(1962-),男,副教授.研究方向:精密检测及控制.E-mail:m2005sh@163.com

Structural Design Optimization Method for Moving Parts of Machine Tool Based on Equivalent Static Load TheoryDUAN Pengyun1,DING Xiaohong2

(1.Public Experiment Center,University of Shanghai for Science and Technology,Shanghai 200093,China;

2.School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：In order to ensure the machining accuracy and cutting efficiency,the moving parts of a machine tool not only need to be of higher stiffness in the cutting process,but also is required to have a light weight so as to reduce the inertia and deformation due to the self-weight during the fast moving process.As a typical design example,the headstock of a bevel gear grinder was studied.A flexible multi-body dynamics finite element model including the components of headstock,electric spindle grinding head,ballscrew and so on was established.The flexible multibody system dynamic analysis was combined with the static structure optimization theory based on the equivalent static load theory and the topology optimization design was performed on the headstock.Compared to the traditional topology optimization design of the headstock based on the static load,the proposed lightweight design method is suitable for moving parts of machine tool.The results show that the weight of the headstock is decreased by 8.5% while the static and dynamitic performance maintain nearly unchanged.

Key words：moving parts of machine tool; equivalent static load; light weight; structural topology optimization

基金项目：上海市自然科学基金资助项目(12ZR1420700)

收稿日期：2014-05-16

DOI：10.13255/j.cnki.jusst.2015.06.015

文章编号：1007-6735(2015)06-0589-05

中图分类号：TH 122

文献标志码：A