受限方腔内绕流两圆管强制对流换热的数值研究

张光璐,　李起耘,　王治云,　严祯荣,　陆廷安,　杨　茉

(1.上海理工大学 能源与动力工程学院,上海　200093; 2.上海市浦东新区特种设备监督检验所,上海　200136;

3.上海市特种设备监督检验技术研究院,上海　200333)



受限方腔内绕流两圆管强制对流换热的数值研究

张光璐1,李起耘2,王治云1,严祯荣3,陆廷安2,杨茉1

(1.上海理工大学 能源与动力工程学院,上海200093; 2.上海市浦东新区特种设备监督检验所,上海200136;

3.上海市特种设备监督检验技术研究院,上海200333)

摘要：针对热电冷综合利用系统中的集热箱,抽象出一个受限方腔内两圆管的强制对流换热问题并进行了数值研究.分别对不同雷诺数Re以及不同管间距s的情况进行数值模拟.结果表明,Re较小时流体流动与换热随时间变化，最后趋于一个稳定的对称状态;当Re增加至一定值后,流体流动与换热随时间变化，处于非对称状态.随着Re的增加,流动出现振荡,流体与圆管壁面换热不断增强,计算得到的解从定态解发展为周期性振荡解、多倍周期振荡解,最终发展为混沌.对于不同管间距s,当Re≤150时,管子间距的不同对受限腔内的换热影响不是很大;当200≤Re<300时,管间距s对于流动与换热有较大的影响;但当Re≥300之后,管间距s对换热影响较小.

关键词：方腔; 加热圆管; 强制对流; 数值模拟

冷热电联供的能量综合利用系统或储能系统中通常会有一个集热箱.一般集热箱中充满流体(如水)并且有流体的流进和流出.一些加热管放置在集热箱的流体当中对流体加热,并由流出集热箱的流体将热量带走.本文研究的受限方腔内绕流两圆管强制对流换热,即是从这种集热箱中的换热问题抽象出来的研究模型.

工业中应用很多的换热设备,如锅炉过热器、省煤器及空气预热器等的换热为绕流管束强制对流换热,与本文研究的模型的不同之处是这些换热设备通常有大量管束,边壁影响一般可忽略,并且各根管子的换热基本相同.例如,Guimaraes[1]和雍青青等[2]由于模型管束较多,使得边壁对圆管流动换热的影响相对较小,因此,在流动方向上引入了周期性充分发展的概念,简化了模型,研究了不同雷诺数下的流场和温度场.而本文研究模型的管子比较少,各根管子的换热不尽相同,互相影响,并且管子位置、受限方腔几何结构等都对流动和换热产生影响.对受限方腔中的自然对流和混合对流已有研究成果报道.Karimi等[3]针对封闭水箱内含两加热圆管的自然对流换热进行了数值模拟,对其中的流场、温度场、传热特性及其非线性特性进行了研究.肖瑞雪等[4]模拟了内置一个发热圆的方腔内热质双扩散混合对流,得出平均努塞尔数Nuav和平均舍伍德数Shav随着理查德数Ri、路易斯数Le和浮升力比Br的变化规律.Hussain等[5]研究了封闭方腔内含一个加热圆管的自然对流问题,分析了瑞利数Ra、圆柱位置及直径大小等参数变化对系统换热的影响.对于本文所抽象的模型,目前相关的研究资料很少.

除了工程背景外,从理论研究的角度来说,本文所抽象的研究模型还有一个特点，由于在流动方向上的后面管子处于前面管子的尾流当中,前面管子形成的尾流影响后面管子的换热，而后面管子会影响前面管子的尾流形成,对前面管子的换热亦有影响.通常情况,绕流圆管形成的尾流会出现振荡和混沌等非线性的现象,因此,本文抽象的研究模型的流动与换热与非线性特性相关.特别是当几何结构发生变化时,会表现出一些非线性现象.郑建城等[6]、申春赟等[7]对圆内开缝圆自然对流换热进行了数值模拟,分析了在不同参数下出现的定态解、周期性振荡解、拟周期性振荡解和非周期性振荡解等非线性特性.张昆等[8]采用紧致差分方法对不同Ra下封闭圆内的自然对流及其分岔现象进行了数值模拟.

本文采用非稳态模型对受限方腔内绕流两圆管的强制对流进行数值模拟,探讨随着Re的变化,流场、温度场及换热的Nuav的变化及其中的非线性现象,并对不同管间距下的模型进行数值模拟,探讨几何结构变化时两圆管间换热和非线性特性的互相影响,为进一步的理论研究与工程应用奠定基础.

1问题和数值方法

1.1物理模型

受限方腔内绕流两圆管强制对流换热如图1所示.方腔四周壁面为绝热,其中放置的两个圆为加热圆管,壁面温度恒定为TH,圆管直径为d.方腔为正方形,相对边长L/d=10,两圆相对管间距s/d=3.温度为Ti的流体由左侧进口以速度ui流入方腔内,与两个温度为TH的圆管进行对流换热后,由右侧出口流出,TH>Ti.正方形腔的进口和出口完全对称,取相对高度h/d=1.假设受限腔内的流体为水,常物性不可压缩流体,取普朗特数Pr=7.0,流动和换热为二维,流体在固体壁面上无滑移.

图1　物理模型

1.2控制方程和边界条件

根据动量、能量、连续性方程,给出无量纲控制微分方程为

(1)

(2)

(3)

(4)

边界条件为

进口截面:

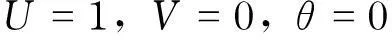
(5)

固体壁面:

(6)

圆管壁面:

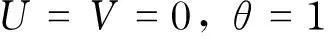
(7)

出口截面:

(8)

以上无量纲参数定义为

式中:x和y分别为水平和竖直方向的坐标;t为时间;u和v分别为水平和竖直方向的速度分量;T,p分别为温度和压力;a,ν,ρ分别为热扩散系数、运动黏度和密度.

不同时刻下加热圆管表面的Nuav为

加热圆管表面的时均努赛尔数

式中，φ为以圆管圆心为原点时，不同圆管表面位置的极坐标值.

本文数值计算采用非稳态模型进行直接模拟,压力和速度的耦合选用SIMPLE(求解压力耦合方程的半隐方法)算法,采用具有三阶精度的QUICK格式对动量方程和能量方程进行离散.本文计算采用残差判定收敛,动量方程的收敛判据为10-3,能量方程的收敛判据为10-6.为确保计算的准确性,对其进行了网格独立性检验,网格数分别取60×60,80×80,100×100,120×120,140×140,160×160,其他网格数下的时均努塞尔数与网格160×160的结果相比,差别最大为3.9%,最小为0.014%,最终选定网格数为140×140.

1.3数值方法验证

目前还没有方腔内绕流两圆管强制对流换热的实验资料.本文用大空间内流体绕流单管强制对流换热的实验资料来检验本文计算方法的可靠性.文献[9-10]给出的绕流单管强制对流换热的实验关联式分别为(Re>105)

Nut=CRenPr1/3

(9)

(10)

图2给出了本文对大空间内流体绕流单管强制对流换热直接数值模拟得到的时均努塞尔数(图2为Nut,DNS,并与文献[9-10]给出的式(9)和式(10)计算得到的Nut.9和Nut,10相对比.由图2可见,数值模拟结果与实验关联式计算结果在Re≤104时吻合得很好,但Re>104后,本文计算的结果与实验结果逐渐偏离.笔者认为,由于本文采用直接模拟,在Re>104后，湍流的影响越来越大,直接模拟不足以给出比较恰当的结果.因此,本文下面讨论的工况范围为Re≤104.

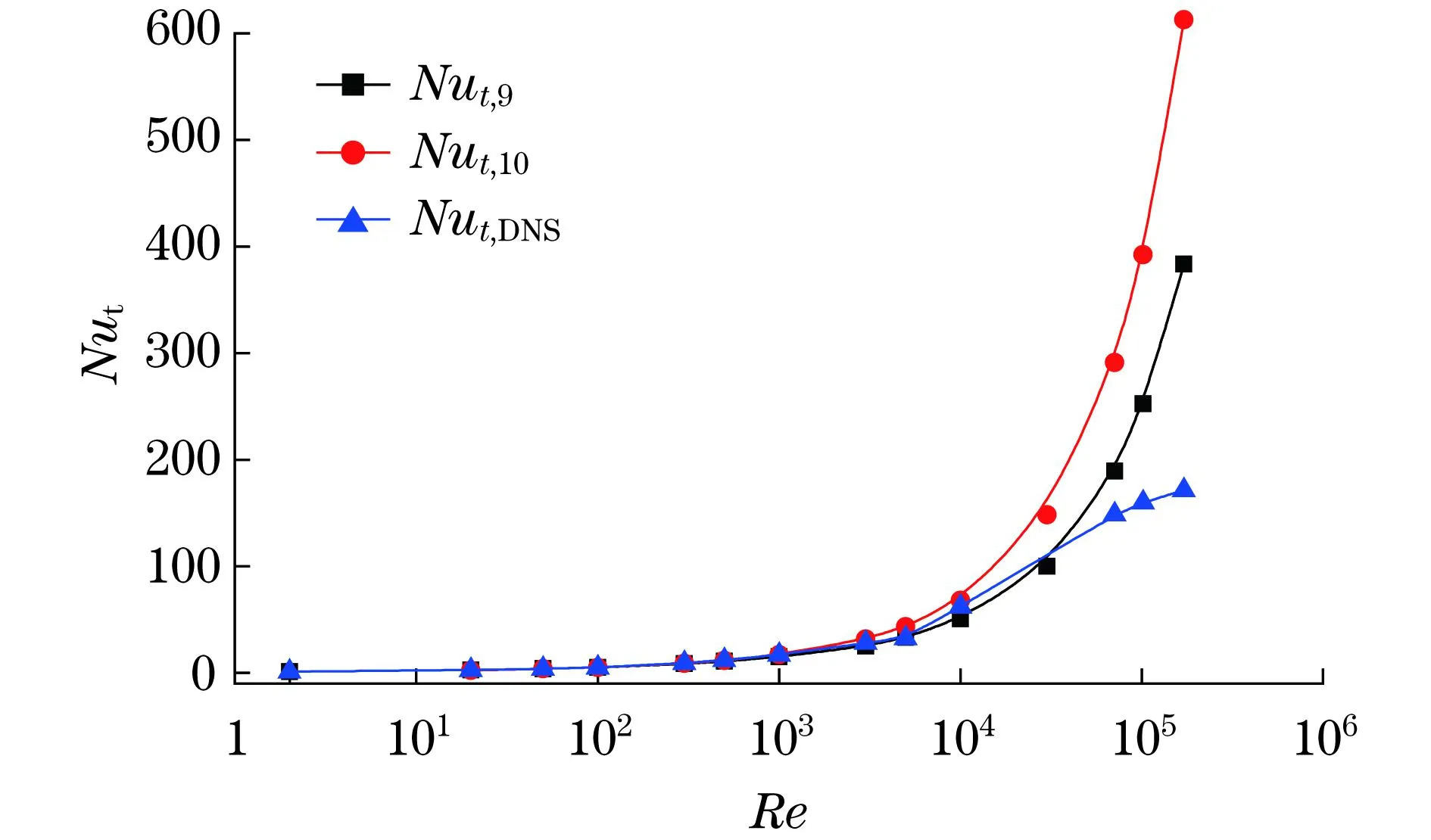
图2　大空间内流体强制对流绕流单管算法验证

2计算结果及讨论

首先固定几何结构,取L/d=10,s/d=3不变,改变Re,分别取Re=50,100,150,180,200,220对该问题进行数值模拟,给出不同Re下的流场和Nuav,并对其中出现的非线性现象进行分析;然后L/d=10不变,比较不同管间距s对流动换热产生的影响,分析管与管之间的互相影响.

2.1流场

图3给出的是L/d=10,s/d=3时不同Re下的流线图.由图3可见,当Re=50时,方腔内流场结构是上下对称结构,在左上和左下位置出现两个对称结构的涡,由于Re较小,在遇到第一个圆管后流场是向外发散,最后由出口流出.随着Re的增加到100时,主流体紧贴两根圆管流出,上下对称结构的涡随着Re的增加向出口处移动.Re继续增大至150,系统流场依然是上下对称结构,但相比Re=100时,上下对称结构的涡不断向出口处移动.当Re=180时,系统所有边界条件都是对称的并与时间无关的,但是,整个流场已经出现不对称现象,此时的不对称只是出现在两根圆管间的内部流场中.由于内部流场的不对称,使得两圆管换热增强,圆管之外的外部流场还是基本对称的.当Re=200时,流场是整体不对称,流动换热增强,由于流速增加,流体向出口处挤压,因此,在出口处流动剧烈,并出现回流现象,增强换热.当Re增大至220时,流体流动更加剧烈,不仅在出口处出现几个漩涡与回流,并且在系统的左半部分也出现几个大小不等的涡.

2.2流体流动换热及其非线性特性

在L/d=10,s/d=3时,对不同Re下的左右两圆管壁面的Nuav进行分析,如图4所示.当Re增加至180后,出现了周期性振荡现象,当Re≥200时,随着时间推移是非周期性振荡,出现混沌现象.

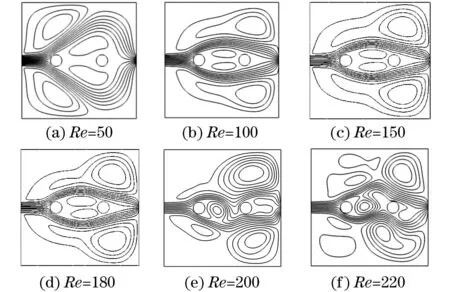
图3　Re=50,100,150,180,200,220时的流线图

图4为左右两圆管的Nuav随时间的变化关系图,随着Re的增大,受限腔内圆管的Nuav逐渐增大,但整体来说,在相同Re下,左侧圆管的Nuav比右侧圆管的要大,这是由于流体由入口处进入横掠左侧圆管,而右侧圆管位于左侧管壁后面的尾流区内,因而影响了换热效果.当Re=50,100,150时,左右两圆管的Nuav在某一时间后都逐渐接近某一恒定值且保持不变.

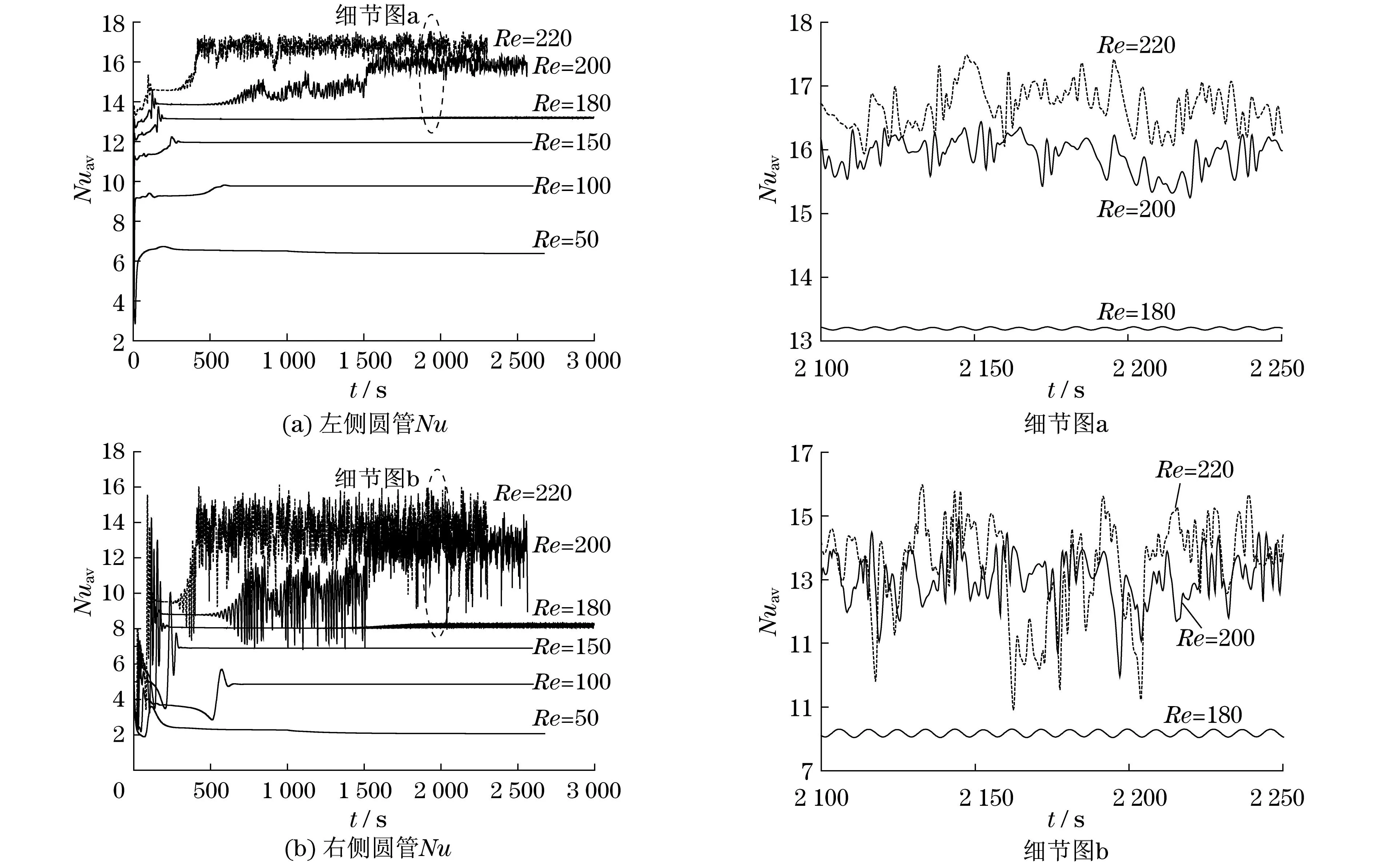
图4　圆管Nuav随时间变化

与Re=150相比,Re=180时,虽然两侧圆管的Nuav增大不多,但是,流动与换热发生了本质性变化,这是由于两圆管间存在一个很小的不对称现象,使其相互不断影响,随着时间推移进入了周期性振荡状态.从图4中可以看出,Re=200时,随着时间推移Nuav逐渐进入无周期性振荡,而Re=220时Nuav进入无周期性振荡的时间与Re=200相比要短,振幅变化较大,因此,与Re=200时相比,Nuav增大较多,换热与流动明显增强.由于后面管子在前面管子的尾流当中,在流动方向上前一根管子形成的尾流影响后面管子的换热,而后面管子影响前面管子的尾流形成,对前面管子的换热也有影响.对比图4(a)和4(b)可以看出,右侧圆管在Re=180,200,220时,Nuav随着时间变化的振幅明显比左侧圆管大很多.

图5分别为Re=150,180,220时受限腔内一随机监测点的无量纲速度相图.由图4可以看出,Re=150时,Nuav变化随时间趋于一个定值,当达到一定的速度后就不再变化.对应图5(a)相应Re下,其速度相图中速度轨线也是收敛于一点,流体的流动换热是稳定的.Re增大到180时,随着时间推移,Nuav作周期性变化，如图4所示,由于其出现的是倍周期变化,因此,由图5(b) 得到几个封闭的圆环.Re=220时,Nuav随时间是作非周期性变化,速度轨线开始变得复杂,其无限次重叠、靠近,但是，永不相交,系统表现出了混沌特性,如图5(c)所示.从图5可以看出,随着Re的增加,计算得到了稳定解之后发展为周期性振荡解,最后发展为混沌现象,与图4所得出的结果相吻合.

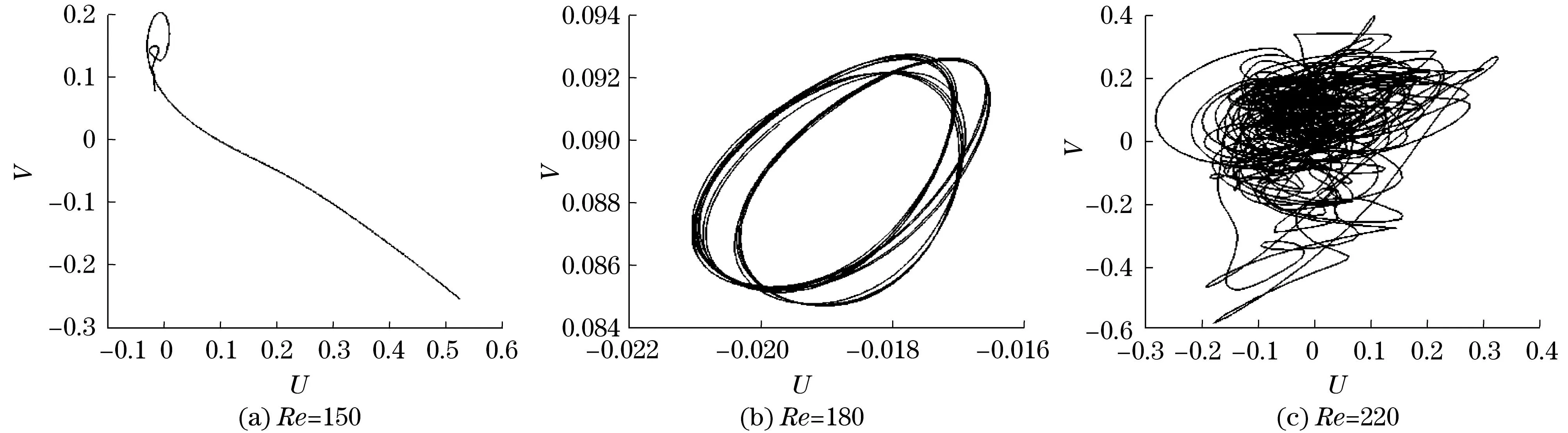
图5　Re=150,180,220时监测点的速度相图

2.3管间距对时均Nut的影响

图6给出了Nut随管间距变化的数值模拟结果.图6(a)给出的是流动方向上前面一根管子的情况(图1左面一根管),图6(b)给出的是流动方向上后面一根管子的情况(图1右面一根管).由图6可见,前一根管的Nut较大,表明换热较强.

由图6可见,管间距对换热的影响还是很明显的,表明两个管子之间的换热互相影响.特别是Re=200左右的时候,管间距变化对换热影响较大.笔者认为,Re≥180时,如前所述,流动发生了振荡,并且流场是非对称的结构,这表明流动出现了湍流或向湍流过渡.由于流动振荡情况对管间距比较敏感,因此,换热受管间距影响较大.从图6还可见,管间距变化时换热的增强和减弱不是单调变化的,这同样可以解释为管子尾流振荡情况不是单调变化的.

3结论

a. 随着Re的增加,受限方腔内流体流动更加剧烈,流体与圆管壁面换热不断增强,Re较小时流体流动与换热随着时间变化最后趋于一个稳定的对称状态.当Re增加至180之后,流体流动与换热随时间变化处于非对称状态.

b. 在L/d=10,s/d=3时,两根圆管间换热互相影响,不同Re下左、右两侧圆管的Nuav随时间而变化,当Re≤150时，流动与换热不随时间变化,最后趋于一个稳定状态;当Re≥180时,左右两侧圆管Nuav出现周期性振荡现象;当Re进一步增加时,流动与换热进入混沌状态.

c. 当200≤Re<300时,管间距s对流动与换热有很大的影响,随着Re的增加，管间距s越大,流动与换热越强;但当Re≥300之后,两圆管的Nut受管间距的影响较小.

参考文献：

[1]Guimarães P M,Da Silva C E S.A parametric study of forced convection in an enclosure with stationary heated cylinders[J].International Communications in Heat and Mass Transfer,2010,37(5):469-475.

[2]雍青青,杨茉,苏丹,等.横掠管束周期性充分发展通道内流动与换热的非线性特性[J].水资源与水工程学报,2014,25(3):29-33.

[3]Karimi F,Xu H T,Wang Z Y,et al.Numerical simulation of unsteady natural convection from heated horizontal circular cylinders in a square enclosure[J].Numerical Heat Transfer,2014,65(8):715-731.

[4]肖瑞雪,李贝贝,徐洪涛,等.内置发热圆的方腔内双扩散混合对流数值模拟研究[J].上海理工大学学报,2014,36(2):170-176.

[5]Hussain S H,Hussein A K.Numerical investigation of natural convection phenomena in a uniformly heated circular cylinder immersed in square enclosure filled with air at different vertical locations[J].International Communications in Heat and Mass Transfer,2010,37(8):1115-1126.

[6]郑建城,杨茉,黄夫泉,等.封闭圆内开缝圆自然对流的非线性特性研究[J].工程热物理学报,2012,33(2):308-310.

[7]申春赟,杨茉,王津,等.圆内开缝圆不同开缝方向自然对流换热[J].上海理工大学学报,2013,35(5):425-429.

[8]张昆,杨茉.紧致方法对流动换热及静态分岔的模拟[J].工程热物理学报,2012,33(1):109-112.

[9]杨世铭,陶文铨.传热学[M].北京:高等教育出版社,2006.

[10]Churchill S W.Bernstein M.A correlating equation for forced convection from gases and liquids to a circular cylinder in crossflow[J].ASME,Transactions,Series C:Journal of Heat Transfer,1977,99(1):300-306.

(编辑:石瑛)

第一作者： 王刚(1991-),男,硕士研究生.研究方向:先进功能材料传热应用研究.E-mail:wanggang_usst@163.com

Numerical Simulation on Forced Convection in a Square Cavity Containing Two Heating CylindersZHANG Guanglu1,LI Qiyun2,WANG Zhiyun1,YAN Zhenrong3,LU Tingan2,YANG Mo1

(1.School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China;

2.Shanghai Pudong Institute of Special Equipment Inspection,Shanghai 200136,China;

3.Shanghai Institute of Special Equipment Inspection and Technical Research,Shanghai 200333,China)

Abstract：Numerical method was used to study the heat transfer of heat collector of a domestic heating power cooling integrated utilization system (DHPCIUS).The unsteady forced convection of two heated horizontal cylinders confined in a 2-D squared enclosure was studied and abstracted to a model by using the DHPCIUS.The simulations were carried out under different Reynolds number Re and cylinders spacing s.The results show that when the Re is smaller,the fluid flow and heat transfer finally tend to a stable and symmetrical state.When the Re increases to a certain value,the fluid flow and heat transfer change over time,being in an asymmetric state.The flow fluid and the heat transfer on the cylinders surfaces are enhanced when the Re increases.The calculations got a stable solution,a periodic oscillation and a direct entering into chaos along with the increase of Re.The cylinder spacing s has a little influence on the flow and heat transfer when Re≤150,while has a great influence on the flow and heat transfer when 200≤Re<300.But when Re≥300,the cylinder spacing affects less on heat-exchange.

Key words：square cavity; heating cylinder; forced convection; numerical simulation

通信作者：贾志海(1975-),男,副教授.研究方向:先进功能材料在动力工程领域的应用.E-mail:zhhjia@usst.edu.cn

基金项目：国家自然科学基金资助项目(51176123);上海市自然科学基金资助项目(11ZR1424800);教育部高等学校博士学科点专项科研基金资助项目(20103120120006)

收稿日期：2014-10-18

DOI：10.13255/j.cnki.jusst.2015.06.009

文章编号：1007-6735(2015)06-0557-06

中图分类号：TK 124

文献标志码：A