微通道中颗粒惯性聚集的力学特性

李海军,　王　浩,　王企鲲

(上海理工大学 能源与动力工程学院,上海　200093)



微通道中颗粒惯性聚集的力学特性

李海军,王浩,王企鲲

(上海理工大学 能源与动力工程学院,上海200093)

1961年,Segré等[1]通过实验最早发现了颗粒的惯性聚集现象,Segré及之后的研究者认为引发颗粒聚集的升力是由于流场的惯性力作用而产生的,因此它被称为颗粒“惯性聚集(inertial focus of particles)”现象[2].颗粒惯性聚集现象由于在血细胞的筛选、分离方面具有应用前景,最近几年备受关注[3-4].作为一种被动技术,在微通道中操纵细胞和颗粒不需要外加装置和附加力,相比其他被动技术,具有高通量、分离效率高、不损害细胞的活性等优点.此外,将这种特殊的流动现象应用于微流控芯片技术中,可研制出各种固液分离与净化装置[4].

尽管惯性聚集现象最近几年受到人们的极大关注,但其机理仍然未知[5].目前,大多数工作专注于设备和应用的开发,对其机理的研究较少.不能充分理解颗粒在微通道中惯性聚集机理的原因在于研究颗粒受力存在困难.甚至在宏观尺度,颗粒受力也很难用实验测出,大多是数值结果[4-5].

Asmolov[6]利用摄动法中的“渐近匹配展开法”对Navier-Stokes方程求近似解,在理论上获得了颗粒在管道内的力学特性,然而它是基于点颗粒假设,没有考虑颗粒尺寸的影响.Zhou等[5]用实验的方法间接获取了惯性升力系数,但实验过程中忽略了升力系数沿通道截面横向位置的变化,且没有考虑颗粒之间的相互作用.Carlo等[2-3]认为惯性升力系数与通道截面横向位置有关,采用数据拟合的方法给出了较大颗粒粒径尺寸(a/H≥0.22,a为颗粒粒径,H为方形通道截面边长)下惯性升力在不同横向位置的量级特征.文献[7-9]数值研究了惯性升力的空间变化特征,但计算中忽略了颗粒旋转.

本文修正了文献[7-9]的计算模型,使其能计及颗粒旋转的因素.在此基础上,利用CFD(com-putational fluid dynamics)技术,数值研究了单个球形颗粒在微通道中的受力特性,分析了颗粒粒径和通道雷诺数对惯性升力和惯性聚集位置的影响特点及颗粒的旋转对惯性升力和惯性聚集位置的影响.

1计算模型与方法

1.1计算模型

单个刚性球形颗粒在微通道方管中运动的简单示意图如图1所示.方形通道横截面尺寸H×H为50μm×50μm,颗粒为粒径a在4～17.5μm之间的多种不同粒径的颗粒,颗粒与流体密度比为1,即在方管内粒子处于悬浮状态,颗粒随流体运动的速度大小记为up.通道雷诺数Re范围为0.1～160,流体采用20 ℃下的纯水(密度ρ=1.0×103kg/m3,动力粘度μ=0.001 Pa·s),流体流动方向为X轴正向,平均流速记为uf.为了消除通道进出口因素的影响,微通道矩形管入口段长度Le的计算方法[10]为

(1)

这样,可使颗粒中心距离流道进出口的实际长度L大于入口段长度,即L>2Le,以确保颗粒不受入口效应的影响.

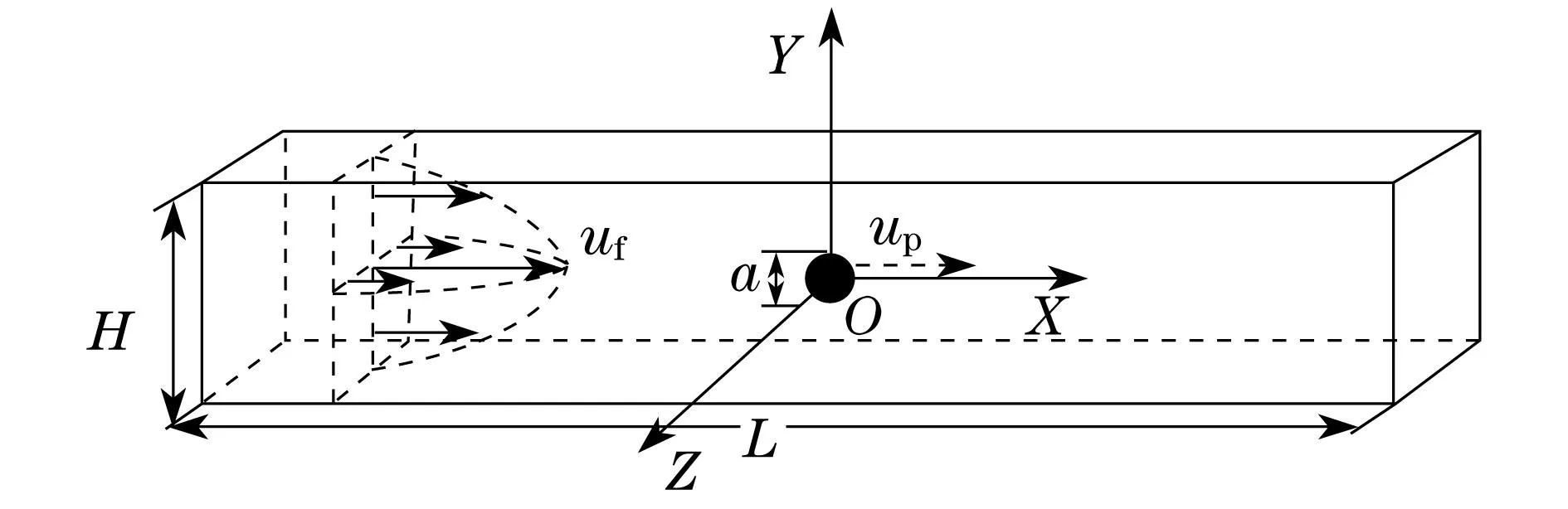
图1　计算模型示意图

为保证计算精度,将方形通道分为三部分:进口区域、颗粒附近区域(以颗粒为中心,边长与方形通道的宽或高相等的立方体区域)、出口区域.在进出口区域生成结构化网格,网格数均为11万;在颗粒附近区域生成非结构化网格,并对颗粒表面及其附近网格加密,网格数为38万,总网格数为60万.文献[8]曾对该计算模型进行过网格独立性验证,并得出总网格数60万满足网格独立性的结论.

1.2计算方法

采用相对运动原理,将非定常、动边界的复杂流场转化为“相对运动模型”下的准定常、固定边界的流场[7-9],相比于“动网格”技术可以大幅度减少计算时间.“相对运动模型”是将参考坐标系建立在颗粒的中心,颗粒被看作静止,流道壁面以速度up反向运动.颗粒沿主流方向的运动速度up通过“试凑法”[3,7-9]近似确定,即通过改变up的大小,使颗粒受到主流方向上的驱动力Fd在数值精度内为零.“试凑法”的具体操作过程可参看文献[7].

在考虑颗粒的自转时,坐标系依然建立在颗粒中心位置,与颗粒等速平移但不旋转.颗粒的角速度ω以边界条件的形式加以给定,其具体值也是通过“试凑法”近似确定.通过不断改变ω的大小,使颗粒受到的合力矩M在数值精度内为零,若此时驱动力在数值精度内不为零,还需要改变up的大小,最终使颗粒受到的驱动力与合力矩在数值精度内都为零.

在CFD数值模拟研究时,设置如下边界条件:通道壁面为无滑移具有平移运动的壁面,速度为-up;颗粒为具有旋转运动的壁面,旋转角速度为ω;通道的进口处边界条件采用速度进口(velocity-inlet);通道的出口处边界条件采用自由出流(outflow).在Navier-Stokes方程求解过程中,其压力与速度的耦合采用SIMPLEC算法,对流项采用具有三阶精度的Quick格式离散,粘性项采用中心格式离散.

2计算结果与分析

2.1较小粒径颗粒及低Re的惯性升力特性

为便于讨论,将相关参数和惯性升力进行无量纲化:颗粒直径的无量纲参数为a+;通道截面横向位置的无量纲参数为y+;通道中惯性力与粘性力的比值为Re;惯性升力系数为CFL.表达式分别为

(2)

(3)

(4)

(5)

本文定义:a+<0.1的颗粒为小粒径颗粒;Re≤20为较低通道雷诺数;Re≥80为较高通道雷诺数.

为了表明在方形微通道中较小粒径的颗粒在通道雷诺数逐渐增加的过程中,可以实现由不聚集到聚集的转变,图2提供了刚性球形颗粒在a+为0.08,Re为20～160时受到的惯性升力沿截面横向位置的分布情况.颗粒的不聚集到聚集转变在图2中表现为惯性升力系数在正转负的过程中由多个零点变为唯一的零点(惯性升力系数为零的点所在截面的横向位置即为聚集位置),然而即使出现聚集现象,其惯性升力也具有较大的波动性.较小粒径颗粒惯性升力具有波动性的原因可能是其在截面横向位置有多个零点,而这些零点对外界的扰动比较敏感,使得颗粒在零点和非零点之间反复迁移.

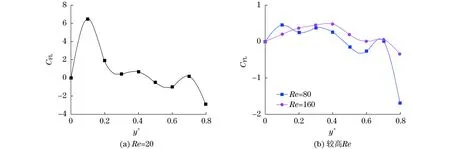
图2　小粒径颗粒惯性升力的横向分布(a+=0.08)

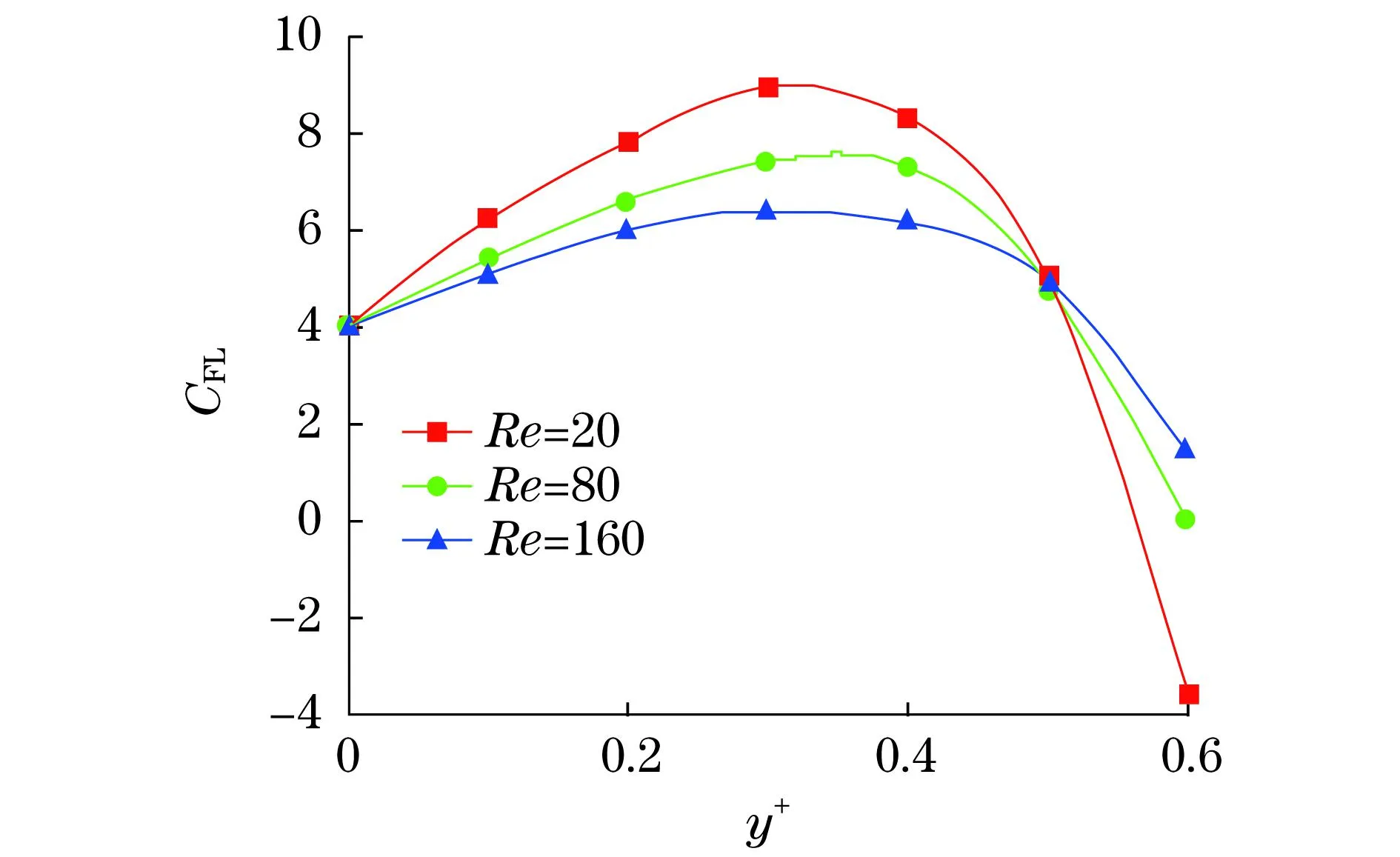
可以发现,随着Re的减小,惯性升力系数在通道轴心处和壁面处增大比较明显,而在横向无量纲位置0.3

为了研究通道雷诺数对惯性升力的影响,图3提供了a+=0.35的颗粒在不同Re下惯性升力在通道截面的横向分布.当Re较小时,颗粒不会出现惯性聚集现象;随着Re增大,颗粒由不聚集过渡到聚集,在图3中表现为惯性升力系数由两个零点转变为唯一的零点,并且横向升力由不规则、具有较大波动性转变为光滑、有规律的截面横向分布,在此情况下的聚集点称为稳定聚集点.

2.2惯性聚集位置的影响因素

先前的研究[2-4,7-9]均未讨论旋转对聚集位置的影响,图4提供了不同粒径的颗粒在Re=80的情形下考虑旋转效应和不考虑旋转效应的惯性聚集位置对比图.研究发现,旋转效应使得聚集位置向通道壁面处移动,这与Zhou等[5]、Matas等[11]的实验结果是一致的,然而他们的实验结果中并没有说明旋转效应对聚集位置的影响及影响程度.在本文研究中发现,与不考虑颗粒自转时的惯性升力相比,具有自转效应颗粒受到的惯性升力有明显增加,且其最大位置向通道壁面处移动,此外聚集位置向壁面处有较明显的移动距离.

图3　颗粒在较低Re下惯性升力的横向分布(a+=0.35)

同时在研究过程中发现,无论颗粒是否旋转,随着颗粒直径的增加,惯性聚集位置都会向通道轴心处移动,而经典的以点颗粒为基础的“渐进匹配展开法”是无法获得此结果的.图4显示了颗粒直径对聚集位置的影响.

图4　旋转对惯性聚集位置的影响

此外,通道Re对惯性聚集位置也有重要的影响,图5给出了a+=0.35时颗粒在不同Re下的惯性升力分布.文献[8]研究发现,在没有考虑颗粒自转的情况下,聚集位置随着Re的增大没有明显的变化.然而本文研究结果表明,随着Re的增大,惯性聚集位置将远离通道轴心,向通道壁面处移动,这些结果与Matas等[11]的实验结果是一致的.随着Re的增大,惯性聚集位置向通道壁面处移动的原因可能是剪切诱导升力增大幅度大于壁面诱导升力的增大幅度，以及旋转诱导升力的增大.

2.3惯性升力系数的分析

为了研究旋转对惯性升力的作用,将惯性升力分解为两部分:一部分为由剪切诱导升力与壁面诱导升力合成的非旋转诱导升力FLS;另一部分为颗粒自转产生的旋转诱导升力FLW.Zhou等[5]在用实验测量惯性升力系数时,也曾将惯性升力分为这两种升力.FLS通过不考虑颗粒的自转效应时获得,FLW可通过在颗粒的自转效应下产生的惯性升力FL与FLS的差值获得,并对这两种诱导升力的系数进行定义:

图5　Re对惯性聚集位置的影响

(6)

(7)

(8)

在旋转效应下,颗粒的惯性升力FL与先前研究[7-9]的非旋转诱导升力FLS在通道截面横向位置的分布是一致的,在图4中表现为颗粒在无旋转时惯性升力系数与旋转情况下惯性升力系数沿截面横向分布具有一致性.惯性升力在通道轴心位置处为零,随着y+的增大而增大,至最大值后开始迅速减小(在图4中表现为惯性升力由正向最大值减小为零,然后力的方向发生改变).进一步研究惯性升力发现,颗粒在壁面附近受到的惯性升力比通道轴心附近受到的惯性升力大很多,其原因可能是由于通道截面上速度分布呈抛物线状,在轴心处速度梯度要远小于壁面处的速度梯度.

图6(a)为Re=80和不同a+下的旋转诱导升力系数,可见该系数随y+呈现规律性变化:先逐渐增大,至最大值后又开始减小,通道壁面处的旋转诱导升力改变速率明显高于通道轴心附近处.图6(b)为颗粒在a+=0.35和不同Re下的旋转诱导升力系数随y+的分布规律,该系数的最大值随着Re的增大而向壁面方向移动.由于旋转诱导升力的方向始终指向通道的壁面方向,因此,颗粒的自身旋转将导致惯性聚集位置向通道壁面处移动.

由于旋转诱导升力的方向始终指向通道壁面,而非旋转诱导升力与惯性升力在截面横向分布具有相同的规律,因此,非旋转诱导升力对惯性升力有决定性的作用,即对颗粒能否产生惯性聚集现象起着决定性的影响.

图6　旋转诱导升力的影响因素

3结论

a. 较小粒径的颗粒在一定的通道雷诺数(Re≤80)下或者大粒径颗粒在较低通道雷诺数(Re<5)下,均不能出现惯性聚集现象；然而当通道雷诺数增加到一定值时,颗粒可产生惯性聚集现象.较小粒径或较低雷诺数下的颗粒受到的惯性升力在通道截面横向位置分布具有较大的波动性.

b. 旋转诱导升力方向始终指向通道壁面, 非旋转诱导升力与惯性升力在通道截面横向位置分布具有一致性,因而非旋转诱导升力对惯性升力起决定性作用.

c. 颗粒的旋转效应对惯性升力有重要的影响,并使惯性聚集位置向通道壁面处移动.此外,在稳定聚集位置存在时,颗粒的惯性聚集位置随着通道雷诺数的增大向壁面处移动,随着颗粒直径的增大向通道轴心处移动.

参考文献：

[1]Segré G,Silberberg A.Radial particle displacements in poiseuille flow of suspensions[J].Nature,1961,189(4760):209-210.

[2]Carlo D D.Inertial microuidics[J].Lab on a Chip,2009,9(21):3038-3046.

[3]Carlo D D,Edd J F,Humphry K J,et al.Particle segregation and dynamics in confined flows[J].Physical Review Letters,2009,102(9):094503.

[4]王企鲲,孙仁.管流中颗粒“惯性聚集”现象的研究进展及其在微流动中的应用[J].力学进展,2012,42(6):692-703.

[5]Zhou J,Papautsky I.Fundamentals of inertial focusing in microchannels[J].Lab on a Chip,2013,13(6):1121-1132.

[6]Asmolov E S.The inertial lift on a spherical particle in a plane poiseuille flow at large channel Reynolds number[J].Journal of Fluid Mechanics,1999,381:63-87.

[7]王企鲲.微通道中颗粒所受惯性升力特性的数值研究[J].机械工程学报,2014,50(2):165-170.

[8]石慧霞,王企鲲.微通道中颗粒惯性聚集特性的数值研究[J].上海理工大学学报,2013,35(4):355-360.

[9]王企鲲,李海军,李昂,等.颗粒惯性聚集中惯性升力的特性研究[J].水动力学研究与进展,2014,29(5):530-535.

[10]计光华,计洪苗.微流动及其元器件[M].北京:高等教育出版社,2009.

[11]Matas J P,Morris J F,Guazzelli É.Inertial migration of rigid spherical particles in poiseuille flow[J].Journal of Fluid Mechanics,2004,515:171-195.

(编辑:董伟)

第一作者： 张光璐(1989-),女,硕士研究生.研究方向:传热及数值技术.E-mail:zglfighting@163.com

摘要：为揭示微通道内悬浮颗粒惯性聚集现象的机理,基于相对运动原理,利用数值方法研究了单个球形颗粒在方形微通道中的运动状况,并对颗粒的受力特性进行分析.研究发现:较小粒径的颗粒在较高通道雷诺数下可产生惯性聚集现象,但其受到的惯性升力在通道截面横向位置分布具有很大的波动性;惯性聚集位置随通道雷诺数的增大向通道壁面移动,随颗粒粒径的增大向通道轴心移动;颗粒旋转产生的旋转诱导惯性升力使惯性聚集位置向通道壁面移动.惯性升力分为旋转诱导升力和由剪切诱导升力及壁面诱导升力合成的非旋转诱导升力,而后者是惯性升力的决定性部分.

关键词：微通道流动; 颗粒惯性聚集; 惯性升力; 力学特性

Mechanical Characteristics of the Inertial Focus of Particles in MicrochannelLI Haijun,WANG Hao,WANG Qikun

(School of Energy and Power Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：In order to reveal the mechanisms of the inertial focus of buoyant particles in microchannel,the relative motion principle and numerical method were utilized to study the mechanical behaviors of a single spherical particle in rectangular microchannel with squared section,and some discussions were presented.The results show that in terms of particles with fairly small size,as the Reynolds number of flow increases to a certain extent,the inertial focus will appear, while the distribution of inertial lift on particles with fairly small size is instable on the lateral section of flow channel.Both the particle’s rotation and the increased Reynolds number can lead the focus position to move towards the channel wall,while it will move away from the channel wall as the particle’s size increases successively.The inertial lift consists of two components,the rotation induced lift and the non-rotation induced lift.The latter is the decisive component of inertial lift,which is composed by shear induced lift and wall induced lift.

Key words：microchannel flow; inertial focus of particles; inertial lift; mechanical characteristics

通信作者：杨茉(1958-),男,教授.研究方向:流动和换热的非线性特性研究.E-mail:yangm@usst.edu.cn

基金项目：国家自然科学基金资助项目(51276118);上海市质量技术监督局公益科研项目(2012-41,2012-12);上海市教委科研创新项目(14ZZ134)

收稿日期：2014-09-24

DOI：10.13255/j.cnki.jusst.2015.06.008

文章编号：1007-6735(2015)06-0551-06

中图分类号：O 352

文献标志码：A