新的四维超混沌系统的Hopf分岔分析与分岔控制

张中华，付景超

(东北电力大学理学院，吉林吉林132012)

自1963年，美国著名气象学家E.N.Lorenz在刻画热对流不稳定性时发现了第一个混沌系统以来，许多新的三维混沌系统被发现，像 Chen系统［1］、Lü系统［2］、Chu系统［3］等等，对这方面的研究也很多［4－7］。此外，电力系统中也存在Hopt分岔。文献［8］给出了求解电力系统动态电压稳定Hopt分岔点的新型混合方法。文献［9］基于中心流形理论对一类小水电并网系统的Hopt分岔进行了分析。文献［10］在Lü系统的基础上，通过设计一个非线性反馈控制器建立了一个新的四维非线性系统，通过Lyapunov指数研究了系统的超混沌行为，并设计自适应控制器控制这种混沌现象。文献［11］在文献［7］的基础上，研究了一个四维超混沌系统的分岔行为，并进一步判定系统分岔的方向和周期解问题。但以上文献没有对超混沌系统的分岔行为进行控制。

本文在文献［10］和文献［11］的基础上，进一步研究四维超混沌系统的分岔控制问题。利用中心流形理论将四维系统降到二维系统，通过研究二维系统的Hopf分岔类型来判定原系统的分岔特性;接着对系统产生的Hopf分岔行为进行极限环幅值(周期解振幅)控制，找出控制参数与幅值之间的关系式，进而判定控制参数对系统极限环幅值的影响。

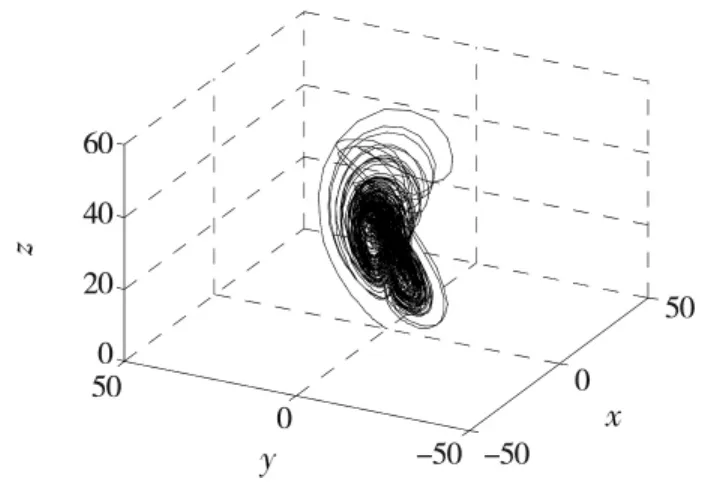
图1 系统(1)的混沌相图

1 系统模型稳定性分析

系统模型如下［11］

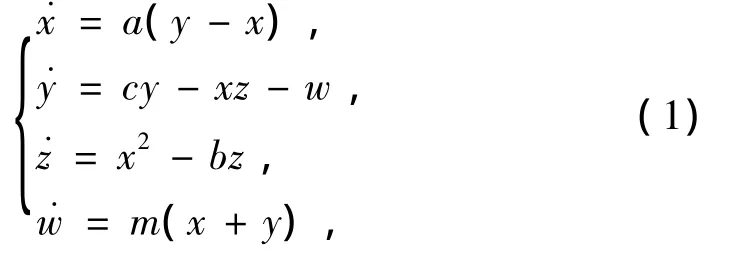
其中，a，b，c，m 是实参数，当 a=36，b=3，c=20，m=7时，系统(1)存在超混沌吸引子，如图1所示。

当b＞0时，系统(1)有唯一平衡点O(0，0，0，0)，下面讨论平衡点O的稳定性问题。系统(1)在平衡点O的线性化矩阵为

相应的特征方程为

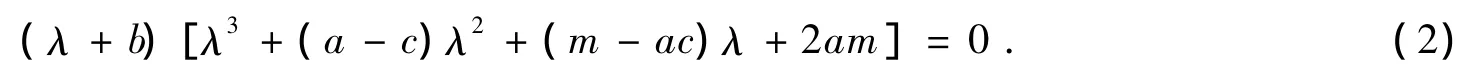
式(2)有一个负根λ3=-b＜0，由Routh－Hurwitz矩阵知:

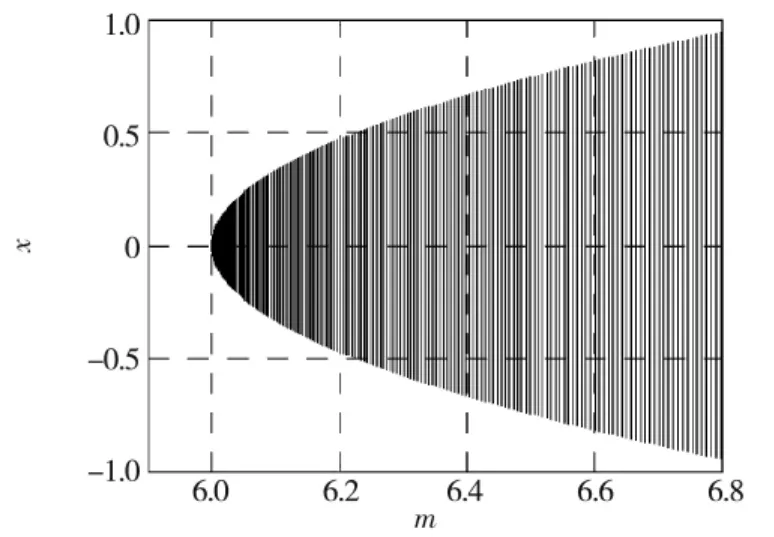
图2 系统(1)在O处的分岔图

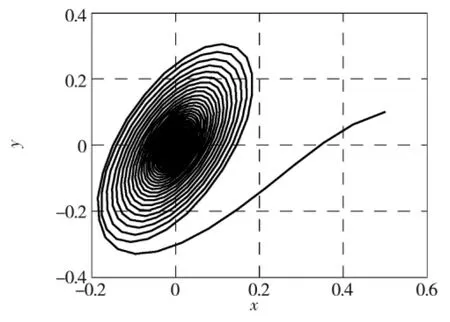
图3 m=5系统(1)在分岔点O处的相图

2 系统Hopf分岔类型判定

当b=3，a=2，c=-1，m=6时，系统(1)在平衡点O处的线性化矩阵为

对应的特征值为

其中ω0=2.828 4。下面讨论系统(1)在平衡点O的Hopf分岔类型。

对系统(1)两端作线性变换(x，y，z，w)T=Ty，其中 y=［y1，y2，y3，y4］T，T 为分岔点 O 处导算子的特征值对应的特征向量的实部和虚部所组成的变换矩阵。

变换后可得系统(1)的Poincare规范形

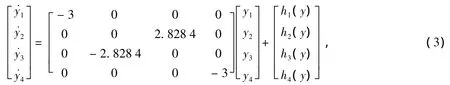
其中:hi(y)(i=1，2，3，4)为包含 y1，y2，y3，y4，m1的非线性部分，m=m1+6。根据中心流形定理，可设式(3)的中心流形为如下形式:

其中:U(y2，y3)和V(y2，y3)为含y2，y3的更高阶项。(0，0)是式(5)唯一有意义的平衡点，由文献［12］知，式(5)与系统(1)有相同的非线性特性，研究式(5)在(0，0)的稳定性及分岔类型相当于研究系统(1)在相应平衡点O处的稳定性及分岔类型。计算式(5)的Hopf分岔稳定性指标

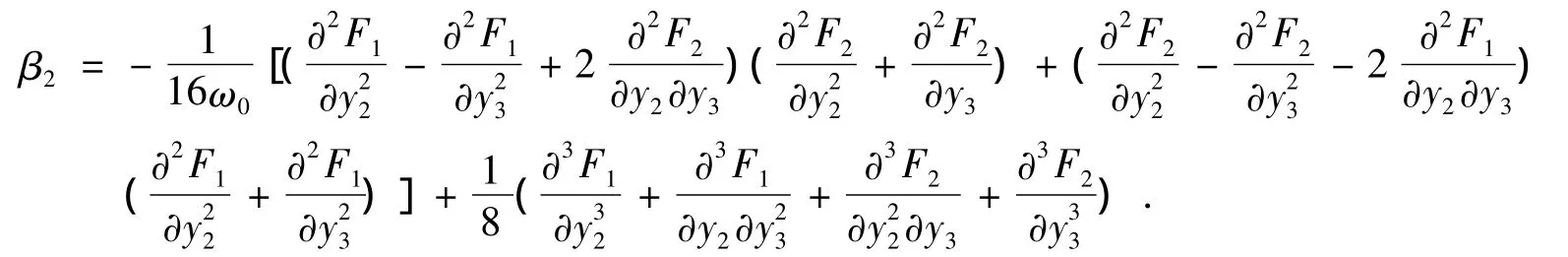
计算得 β2=-0.014 1 ＜ 0。所以，式(5)在(0，0)处发生超临界Hopf分岔，由此可判定系统(1)在分岔点O处发生超临界Hopf分岔，系统O产生等幅振荡，出现稳定极限环，如图4所示，仿真初值为(x0，y0，z0，w0)=(0.5，0.1，0.1，0.1)。

3 分岔控制

不改变原系统的Hopf分岔点，对系统(1)施加基于Washout滤波器辅助的非线性控制器得:

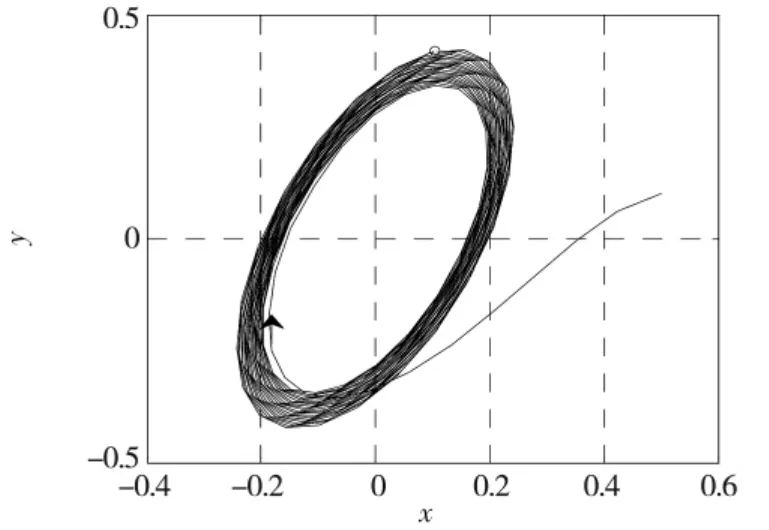
图4 m=6.2时，系统(1)在平衡点O处和相图

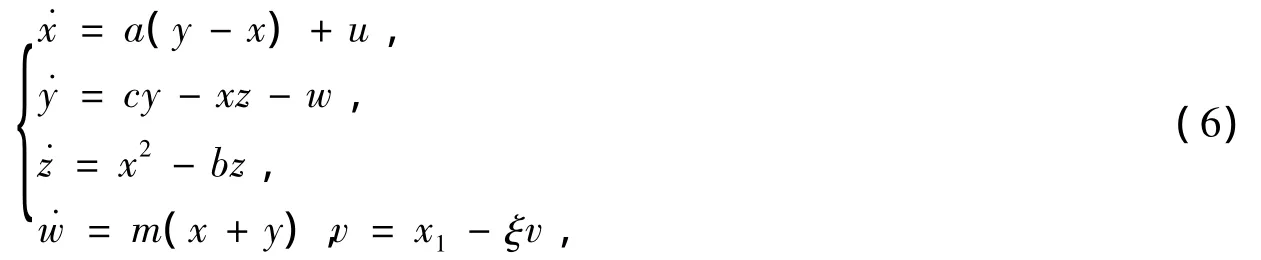
其中 u=k(x1-ξv)3，非线性控制器没有改变原系统的平衡点 O，系统(6)有平衡点~O(0，0，0，0，0)。取b=3，a=2，c=-1，ξ=0.5，m=6，则系统(6)在平衡点 ~O 处的线性化矩阵为

对应的特征值为

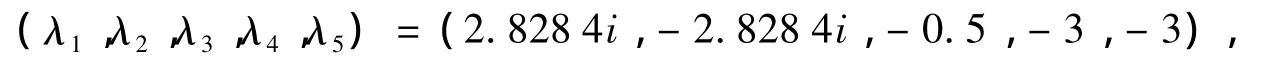
变换后可得系统(6)的Poincare规范形

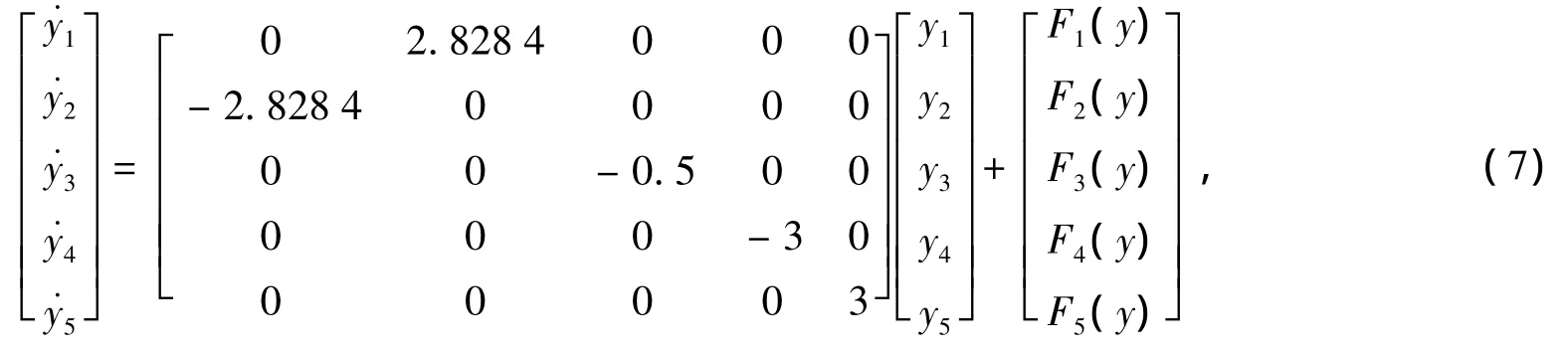
其中 hi(y)(i=1，2，3，4，5)是包含 y1，y2，y3，y4，y5，k 的非线性部分。

根据Hopf分岔理论计算系统(6)的Hopf分岔稳定性指标β［13］2

其中

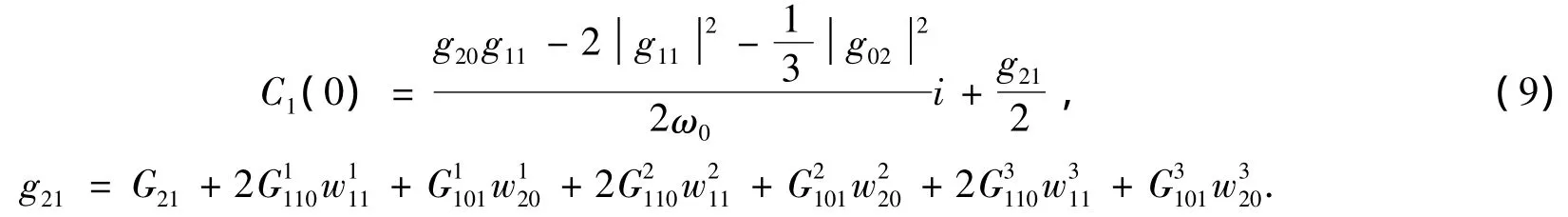
根据式(7)及文献［13］，分别计算各个特征量得

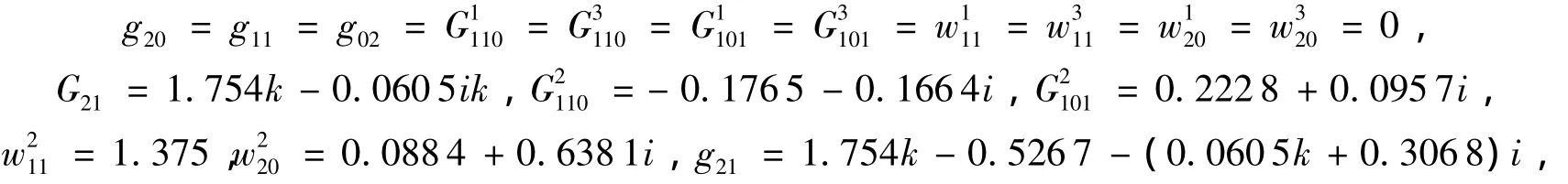
将以上结果代入式(8)和式(9)得

当k＜0.3时，β2＜0，系统(6)发生超临界Hopf分岔，在平衡点附近系统产生等幅振荡，出现稳定极限环，如图5所示。当k=0时，β2＜0，即在施加控制器前系统的分岔类型为超临界，这与2中所分析的结果相符合。另外，极限环幅值(振动幅值)会随着控制参数k的减小而减小，见图5～图6。当k＞0.3时，β2＞0，系统(6)发生亚临界Hopf分岔，在平衡点附近系统产生增幅振荡，出现不稳定极限环，如图7所示。其中，仿真初值为(x0，y0，z0，w0，v0)=(0.5，0.1，0.1，0.1，0)。

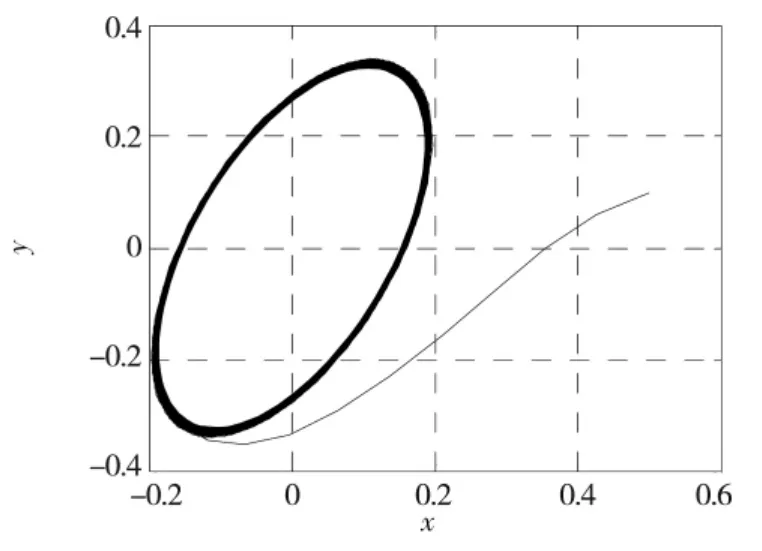
图5 k=0.2时，系统(6)在分岔点~O处的相图

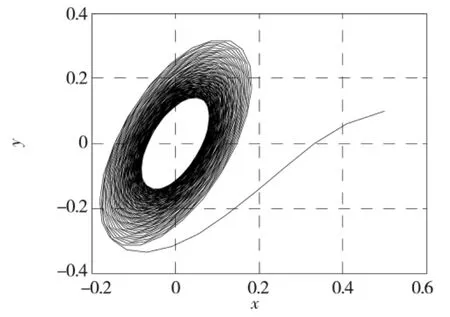
图6 k=－2.5时，系统(6)在分岔点~O处的相图

由以上分析知，当非线性控制参数满足一定条件时，可以改变原系统的Hopf分岔类型和极限环幅值大小，从而实现系统的极限环幅值控制。

图7 k=0.9时，系统(6)在分岔点~O处的相图

4 结 论

本文主要研究了一个新的四维非线性系统的Hopf分岔行为和极限环幅值控制问题。通过中心流形理论判定系统的Hopf分岔类型，然后对系统施加基于Washout滤波器辅助的非线性控制器，讨论了控制器对Hopf分岔类型及极限环幅值的影响。通过讨论得出结论，当非线性控制参数满足一定条件时，可改变原系统的Hopf类型，并能控制极限环幅值的大小。文中用Matlab软件对理论结论进行数值仿真，仿真结果与理论分析结果一致。

［1］ChenGuanrong，T.Ueta.Yet another chaotic attractor［J］.International Journal of Bifurcation and Chaos，1999，9(7):1465－1466.

［2］Lü Jinhu，Chen Guanrong.A new chaotic attractor coined［J］.International Journal of Bifurcation and Chaos，2002，12(3)659－661.

［3］ChuYanddong，Li Xianfeng，Zhang Jiangang，etal.Nonlinear dynamics analysis of a new autonomous chaotic system［J］.Journal of Zhejiang University(Science A)，2007，8(9):1408－1413.

［4］PangShou－Quan，Liu Yong－Jian.A new hyperchaotic system from the Lü system and its control［J］.Journal of Computational and Applied Mathematics，2011，235(8):2775－2789.

［5］AntonioAlgaba，Fernando Fernández－Sánchez，Manuel Merino.Centers on center manifolds in the Lorenz，Chen and Lü systems［J］.Commun Nonlinear Sci Numer Simulat，2014，19(4):772－775.

［6］DengKuibiao，Yu Simin.Hopf bifurcation analysis of a new modified hyperchaotic Lü system［J］.Optik，2013，124(23):6265－6269.

［7］刘洪伟.一类Silnikov方程的Hopf分岔控制［J］.东北电力大学学报，2014，34(4):75－79.

［8］吴金龙，张焰.一种求解电力系统动态电压稳定Hopf分岔点的新型混合方法［J］.东北电力大学学报，2008，28(4):18－24.

［9］张中华，付景超，李鹏松.基于中心流形理论的小水电并网系统Hopf分岔分析［J］.振动与冲击，2015，34(2):50－54.

［10］高智中.一个新的非线性系统及其超混沌控制［J］.浙江大学学报:理学版，2012，39(3):303－307.

［11］Du Wenju，Zhang Jiangang，Yu Jianning，et al.Hopf bifurcation analysis in a Novel nonlinear system［C］.Proceedings of the 32nd Chinese Control Conference，Xi’an，2013，26－27.

［12］张琪昌，王洪礼，竺致文，等.分岔与混沌理论及应用［M］.天津:天津大学出版社，2005，147－150.

［13］Hassard，B.D.Theory and Application of Hopf Bifurcation［M］.Cambridge University，1981.