混沌理论在电力系统负荷预测中应用综述

杨 茂，吕天峰，季本明

(1.东北电力大学电气工程学院，吉林吉林132012;2.吉林华微电子，吉林 吉林132013)

负荷预测对电力系统安全运行有重要作用，其预测精度对调度部门的机组优化组合、经济调度和电力市场有着重要的意义［1］。但影响负荷变化的因素较多，以及电力系统本身的非线性，使电力系统负荷在一定程度上呈现貌似随机的特点，很难建立一个精准描述负荷物理属性及影响因素的预测模型。

混沌是确定性系统中由于随机性而产生的一种外在的、复杂的、貌似无规则的运动。混沌系统对初值敏感［2］的特性使混沌系统输入的变化能迅速地反映在输出中，所以混沌理论提供了一种更符合现实世界的非线性建模方法。目前，已经通过多种方式证实了电力系统负荷存在混沌特性［3－5］。基于混沌理论的负荷预测较好地刻画了负荷物理属性及影响因素，是一种预测精度高、简单、易行的电力系统负荷预测方法。

1 混沌理论预测模型概述

混沌预测模型直接对含有气温、气候和空间等因素影响的负荷的历史数据进行分析，根据得出的客观特征规律进行预测，避免了以往时间序列法、神经网络法、专家系统法和各种预测方法加权组合法等预测方法的人为主观性，具有较高的预测精度和预测可靠性。混沌理论预测一般包含时间序列混沌特性的判别、确定延迟时间与嵌入维数、重构相空间和预测四个流程(如图1)。

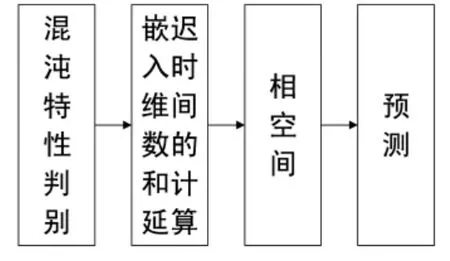
图1 混沌理论预测模型机理流程图

1.1 混沌特性的判别

混沌特性判别是混沌预测模型的第一步，是混沌预测模型的基础。混沌特性判别的依据是:各种运动对应特征量的差异性。如，混沌序列的功率谱为一条有宽峰的连续曲线，而周期运动的功率谱图对应尖峰;混沌序列的主分量谱图为过定点且斜率为负的直线，而噪声的主分量谱图接近平行于X轴的直线。

常用的混沌特性判别方法有定性分析法和定量分析法两类:定性分析法根据混沌序列图谱的形状来判别混沌特性，包括功率谱方法、主分量分析(PCA分布)和Poincare截面法［5］等方法;而定量分析法能给出特征量的数值并以此来判别混沌特性，包括分形维数和最大Lyapunov指数法［6－9］等方法。

1.2 延迟时间τ与嵌入维数m的选取

混沌序列延迟时间τ与嵌入维数m的选取，对相空间重构以及后续的预测具有重要意义。延迟时间τ与嵌入维m的选取可以分为两类:一类认为与嵌入维m是互不相关的，m和τ是独立求得的，如用来计算延迟时间τ的自相关法、复自相关法和互信息法，而G－P算法只求得嵌入维数m;一类认为嵌入维m与延迟时间τ是相关的，同时求得m和τ，如时间窗口法和C－C方法等方法。

1.3 相空间重构

Taken［10］定理认为，时间序列包含了系统状态所需要的全部动力学信息，能够找到一个合适的嵌入维m，在重构后的嵌入维空间里可以把所有规律的轨迹恢复出来，这为混沌序列的预测奠定了理论基础。混沌时间序列重构相空间的方法主要包括导数重构法和坐标延迟重构法等［11］，实际应用中普遍采用坐标延迟重构法。设实际负荷实测时间序列为 {xi，i=1，2，…n}，根据选取的嵌入维m与延迟时间τ，把时间序列拓展成m维相量:

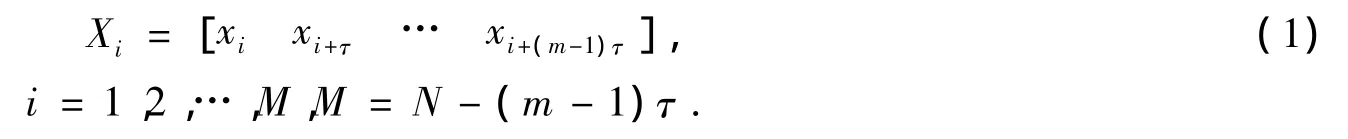
2 混沌预测模型

预测是混沌预测模型的价值出口，其为机组优化组合、经济调度提供理论指导。本文把混沌预测模型分为Lyapunov指数预测模型、局域预测模型、人工智能预测模型以及区间概率预报模型4类(具体如图2)。

图2 混沌预测模型分类

2.1 Lyapunov指数预测模型

Lyapunov指数预测模型是在嵌入相空间中，以相邻相点的轨道发散距离建立预测模型。假设时间序列相空间重构后的相点如公式(1)，XM为参考点，XM+T为XM演化T步后的预报点，Xk为XM的最邻近点，Xk+T为Xk演化T步后的相点，则Lyapunov指数预测模型为:

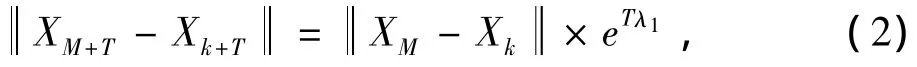
其中λ1为最大Lyapunov指数。

文献［12］以公式(2)建立了一维Lyapunov指数LE预报模型，对东北电网1994年负荷数据进行了预测计算，其预测误差很少有误差大于3% 的。文献［13］将C－C方法应用于小数据量方法，优选了延迟时间τ与嵌入维数m，得到了公式(2)的改进Lyapunov指数预测模型，并对华东电网1999年负荷进行预测，其预测误差基本上控制在2% 以内，而且误差在1% 以内的达83.33%。

传统Lyapunov指数预测具有较高的预测精度和可信度，但预测时间大于预测时限1/λ1时，误差倍增、失去了预测的意义。为此，文献［14］把负荷序列分解为k个不相交的子序列，对各个子序列分别建立Lyapunov指数预报模型，建立了以公式(2)为基础的k－Δt间隔采样模型，延长了有效预测时限。文献［15］用经验模态分解对混沌序列分解，用公式(2)对分解后的子序列作预测，预测的时限变长。

2.2 局域预测模型

与Lyapunov指数预测模型以相邻轨道的发散距离建模不同，局域预测模型是以邻近点的线性演化为基础建立预测模型。假设时间序列相空间重构后的相点如公式(1)，找到XM的N个邻近点Xkj，邻近点的T步演化相点为Xkj+T，由

求出a和b，再由XM+T=a+bXM进行预测。

文献［16］以欧氏距离确定临近域，用最小二乘求得a和b，建立局域预测模型，以华中电网负荷数据为例，其96点的预测误差系数R为0.000 186。文献［17］建立的局域预测模型中，公式(3)中a、b分别为相量A和雅克比阵B，而不再是自然数。通过对某地区电网的有功负荷作预测，其预测的平均误差为0.56%。文献［18］提出了加权一阶局域法，其权值依赖于参考点和邻近点之间的距离，以华东某电网实际负荷数据为例，结果表明加权一阶局域法预测精度高、操作方便，具有较好的实用性。文献［19］在选择临近点时，先以欧氏距离“粗搜索”，再以相关系数的“细搜索”剔除伪临近点，与“粗搜索”局域法相比，平均预测误差提高到0.61%。

2.3 人工智能预测模型

电力系统负荷实际上是受气温、气候、地区等多种因素影响的多维非线性混沌系统，具有复杂且难以准确预测的特征。以混沌相空间理论与神经网络、SVM等理论相结合的人工智能预测模型，与局域预测模型中的线性演化相比，能更好的刻画相点间的非线性演化关系，具有较好的预测精度，是近年来一种被广泛应用的预测模型。

2.3.1 混沌－神经网络预测模型

混沌－神经网络模型是非线性预测模型中最为常用的非线性预测模型之一，它是以邻近域相点为神经网络的训练样本进行训练建模的预测模型，采用经验风险最小化准则，在训练中最小化样本点误差，具有较好的预测性。文献［20］以邻近域相点为BP神经网络的训练样本进行训练建模，实现对负荷的预测。文献［21］建立了以混沌神经元为节点的混沌神经网络模型，以天津配电网和地区网的负荷数据为例，结果证实了改进混沌神经网络模型能有效地提高预测精度。文献［22］把优化邻近点与递归性神经网络相融合的进行预测，提高了负荷预测的精度。

2.3.2 Choas－SVM 模型

Choas－SVM模型也是广泛应用于电力系统负荷预测的模型之一。与混沌—人工神经网络相比，Choas－SVM在最小化样本点误差的同时，缩小模型泛化误差的上界，避免了过拟合现象，提高了模型的泛化能力。文献［23］在嵌入维相空间重构上，以m维相点维训练样本建立了最小二乘支持向量机预测模型。以陕西省某地区负荷为例，其预测相对误差大部分在2%以内。文献［24］用蚁群算法优化了采用高斯核函数SVM中4个参数，其日预测平均预测误差为1.53%。文献［25］将模糊理论运用到Choas－SVM模型中，利用模糊曲线筛选出能代表时间序列发展趋势的数据，大大减少了Choas－SVM的训练样本数量。

2.4 区间概率预测模型

目前大多预测模型的预测结果都是确定性的，只给出一个确定的数值，无法确定预测结果可能的波动范围。但电力系统中蕴含了各种不确定因素，在人员决策时须考虑电力系统的不确定性，因此区间概率预测更加符合客观需求。献［26］用系统聚类法找出当前相点的k个邻近域，用局域预测模型分别对其预测，以最大、最小预测值确定概率预测区间。以北方某地区电网为例，日(24点)预测在置信水平0.98时的准确率为97.82%，平均相对误差为1.75%。

3 总 结

文章概述了混沌预测模型的机理和条件，介绍了几种混沌判别的方法，并简要介绍了数种混沌预测模型。现行的混沌预测模型能够较好的反映电力系统本身的特点、预测精度较高，但大多数预测模型是单步预测，但实际上机组优化组合、经济调度等过程需要相应的时间，超前N步的多步预测要比简单扩大单步预测的时间尺度的效果要好。在多步预测中，混沌序列的多步自适应预测算法能够根据误差自动的调节预测器系数，但还没有广泛应用于电力系统负荷预测，具有进一步研究的价值。

［1］孟祥星，王宏.大规模风电并网条件下的电力系统调度［J］.东北电力大学学报:自然科学版，2009，29(1)，1－7.

［2］Lorenz E N.Deterministic non－periodic flow［J］.Journal of the Atmospheric Sciences，1963，20(2)，130－141.

［3］O’N eill－Carrillo E，Heydt G T，Kostelich E J.Chaotic phenomena in power systems:detection and applications［J］.Electric Machines and Power Systems，1999，27(1)，79－91.

［4］Choi J G，Park J K，Kim K H，et al.Daily peak load forecasting system using a chaotic time series［C］.Proceedings of the International Conference on Intelligent Systems Applications to Power Systems，Orlando，USA，1996，283－287.

［5］Arango H G，de Souza A C Z，Lambert－Torres G，et al.Difference between regular and deterministic chaos processes based on time analysis of load:an example using CEMIG data［J］.Electric Power Systems Research，2000，56(1)，35－41.

［6］吕金虎，陆君安，陈士华.混沌时间序列分析及其应用［M］.武汉:武汉大学出版社，2002.

［7］Rosenstein M T.，Collins J J，De Luca，C.J.A practical method for calculating largest Lyapunov exponents from small data sets［J］.Physica D:Nonlinear Phenomena，1993，65(1)，117－134.

［8］Sano M，Sawada Y.Measurement of Lyapunov spectrum from a chaotic time series［J］.Phys Rev Lett，1985，55(10)，1082－1085.

［9］Wolf A，Swif，J B，Swinney H L，et al.Determining Lyapunov exponents from a time series［J］.Physica D:Nonlinear Phenomena，1985，16(3)，285－317.

［10］Takens F.Detecting strange attractors in turbulence［M］.Springer Berlin Heidelberg，1981.

［11］李智勇，吴为麟.基于相空间重构的电能质量扰动特性提取方法［J］.浙江大学学报:工学版，2008，42(4):672－675.

［12］梁志珊，王丽敏.基于 Lyapunon指数的电力系统短期负荷预测［J］.中国电机工程学报，1998，18(5)，368－371.

［13］吕金虎，占勇.电力系统短期负荷预测的非线性混沌改进模型［J］.中国电机工程学报，2000，20(12)，80－83.

［14］杜杰，陆金桂，曹一家，等.短期电力负荷预报间隔采样混沌模型［J］.中国电机工程学报，2006，26(10)，28－32.

［15］杨永锋，任兴民，秦卫阳，等.基于EMD方法的混沌时间序列预测［J］.物理学报，2008，57(10)，6139－6144.

［16］温权，张勇传.负荷预报的混沌时间序列分析方法［J］.电网技术，2001，25(10)，13－16.

［17］李天云.电力系统负荷的混沌特性及预测［J］.中国电机工程学报，2000，20(11)，36－40.

［18］吕金虎，张锁春.加权一阶局域法在电力系统短期负荷预测中的应用［J］.控制理论与应用，2002，19(5)，767－770.

［19］谷子，唐巍.电力短期负荷时间序列混沌相空间重构参数优选法［J］.中国电机工程学报，2006，26(14)，18－23.

［20］马轶东，何怡刚，王桓.运用BP神经网络的电力负荷混沌多步预测［J］.电力系统及其自动化学报，2010(4)，81－84.

［21］孙雅明，张智晟.相空间重构和混沌神经网络融合的短期负荷预测研究［J］.中国电机工程学报，2004，24(1)，44－48.

［22］张智晟，孙雅明，王兆峰，李芳.优化相空间近邻点与递归神经网络融合的短期负荷预测［J］.中国电机工程学报，2003，23(8)，45－50.

［23］王德意，杨卓，杨国清.基于负荷混沌特性和最小二乘支持向量机的短期负荷预测［J］.电网技术，2008，32(7)，66－71.

［24］张智晟，马龙，孙雅明.混沌理论和支持向量机结合的负荷预测模型［J］.电力系统及其自动化学报，2009，20(6)，31－35.

［25］崔万照，朱长纯，保文星，刘君华.基于模糊模型支持向量机的混沌时间序列预测［J］.物理学报，2005，54(7)，3009－3018.

［26］方仍存，周建中.应用聚类算法和混沌理论的短期负荷概率性区间预测［J］.电网技术，2010，34(11)，65－69.