困难学生认定：基于AHP方法和熵值法的分析

任海华

(南通职业大学外国语学院　江苏南通　226007)



困难学生认定：基于AHP方法和熵值法的分析

任海华

(南通职业大学外国语学院江苏南通226007)

摘要：困难学生认定是开展学生资助工作的前提，是国家、各高校实施学生资助政策中基础性工作，影响着学生资助工作的有效度。在综合分析各综合评价方法的基础上，运用AHP求解评价指标的权重，恰到好处地运用AHP主观赋权的优势；运用熵值法计算各评价组的综合评价，合理地运用数据间内在规律给予的权重；运用以AHP主观赋权与熵值法客观赋权相结合的方法，有力提高认定结果的准确性。

关键词：困难学生； AHP； 熵值法

0引言

困难学生群体的学业问题受到国家、社会以及学校的高度关注，这是社会主义国家公平正义的重要体现。2007年5月，国务院下发《关于建立健全普通本科高校高等职业学校和中等职业学校家庭经济困难学生资助政策体系的意见》，明确国家针对困难学生群体的资助政策。困难学生群体从备受国家、社会以及学校关注阶段跨越到实质性经济资助阶段[1]。教育部、财政部联合下发《关于认真做好高等学校家庭经济困难学生认定工作的指导意见》，明确教育行政部门、各高校学生资助工作的组织管理、程序规范等。《指导意见》并没有给出困难学生认定等具体的操作规范。关于学生资助工作的研究主要集中在两个方向，一方面是宏观、中观视角下学生资助系统的构建研究[2]，资助育人[3]、困难学生心理危机干预[4]等学生资助外延领域研究，而另一方面是微观视角下困难学生认定、甄别方案研究。

学生资助工作的前提和基础是困难学生认定工作，而有关困难学生认定方案研究以现有文献成果来看已初具体系，主要集中在两个研究方向。第一，偏定性判定方向。部分学者研究给出决定学生是否贫困的指标，根据指标给出最后的评价。第二，偏定量分析方向，结合定性判定手段。笔者在文献[5]给出以熵值法构建困难学生认定的数学模型；笔者在文献[6]运用层次分析法(AHP)构建困难学生认定的数学模型。单纯以定性分析方法给出困难学生认定的基本方法，受人为因素影响较大，容易产生偏差；而借助于定量分析的精准特性更加准确地遴选出困难学生群体。

就困难学生认定方案构建研究来看，文献[5]运用熵值法特有的对客观存在数据内在逻辑关系挖掘的特性进行困难学生认定，具有客观判断优势。由于困难学生认定方案的构建问题不只是纯数理定性分析问题，需要定性主观的判断，因此单纯运用熵值法构建困难学生认定方案是不全面的。文献[6]运用定量的AHP方法，具有主观赋值优势。由于困难学生认定方案的构建问题不只是建立在主观赋值基础上，需要客观数理逻辑的判定，因此单纯运用AHP方法构建困难学生认定方案也是不全面的。这两方面研究丰富了困难学生认定领域的成果。

AHP法在定性分析的基础上给出主观赋值，没有脱离事物本身的定性特性。相对而言，熵值法对研究数据的分布形态不需要做任何假定，赋权方式相对比较客观。本研究尝试运用AHP[6~10]求解评价指标的权重，运用熵值法[5,11]计算各评价组内的综合评价，将AHP与熵值法进行有机结合并引入困难学生认定工作中，最终计算困难学生认定综合评价，以此提出基于AHP和熵值法的困难学生认定模型。本研究将AHP与熵值法相结合的方法运用到困难学生认定领域中去具有一定的创新性：充分利用AHP偏于定性主观判断优势与熵值法偏于定量数理逻辑客观判断优势。从当前的文献来看，学者还未将AHP法与熵值法相结合引入困难学生认定领域。

1困难学生认定指标体系构建

根据笔者已有的研究成果，选取基本反映学生情况的关键性指标来构建本研究指标体系，即选取地区状况(AC)、家庭结构(FS)、经济状况(ES)、生活状况(LC)和学习状况(LS)等指标[5]。见图1。地区状况、家庭结构、经济状况属于客观性指标，反映不以学生意志转移的客观经济状况；生活状况、学习状况属于主观性指标，其中生活状况属于主观存在性指标，反映学生真实的生活水平，而学习状况属于主观励志性指标，反映学生的精神状态。因此选取地区状况(AC)、家庭结构(FS)、经济状况(ES)、生活状况(LC)和学习状况(LS)等五个指标能较为全面反映被认定学生的基本情况。

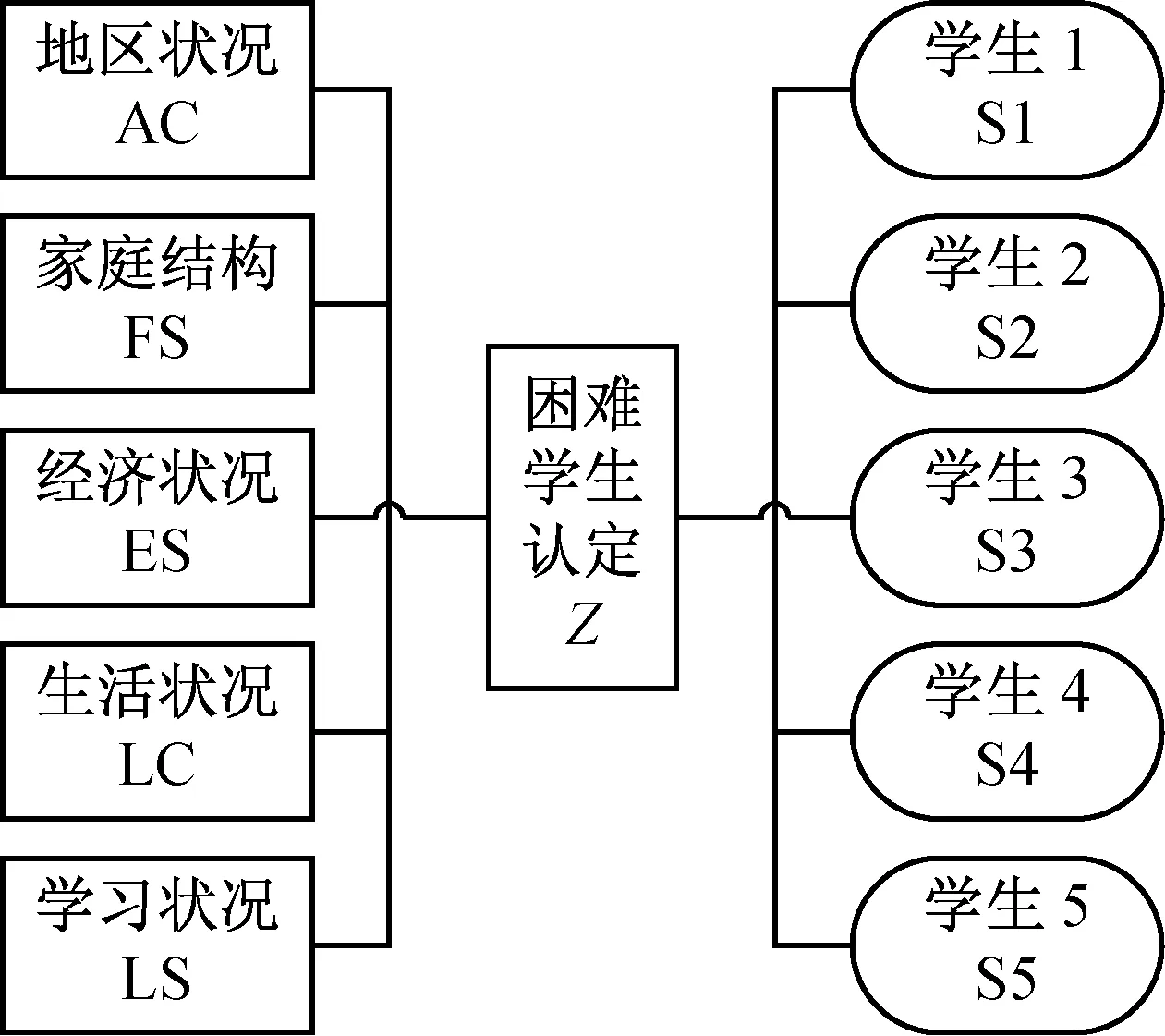
图1　困难学生认定指标体系的结构

为尽可能体现程序的公正性与数据来源的合理性，考虑从学生、政治辅导员、班主任、教师、院系分管领导、院系级资助工作人员、学校其他部门人员和校外专家中抽取代表组建“综合认定专家组”。其中学生是利益相关者，政治辅导员、班主任、教师、院系分管领导以及院系级资助工作人员是开展学生资助工作的主要参与者，这两类人员的参与从主观上确保认定工作的公平合理；其中学校其他部门人员和校外专家的参与，由于利益无关性确保从客观上的公平合理。“综合认定专家组”以召开专家组会议的形式给出判定数据[5]。

2基于AHP法和熵值法的分析的困难学生认定模型

根据AHP和熵值法理论的基本原理，这里建立困难学生认定模型：运用AHP求解评价指标的权重，然后运用熵值法计算各评价组的综合评价，在此基础上计算困难学生认定综合评价数据以得到结论。

2.1　运用AHP求解评价指标的权重

1) 构建分类评价指标判断矩阵。为科学客观确定评价指标的权重，由学生代表组建“朋辈评价组”，由院系分管领导代表、院系级资助工作人员代表、政治辅导员代表、班主任代表组建“学院评价组”，由教师代表组建“教师评价组”，由学校其他部门人员代表、校外专家代表组建“第四方专家组”，由组建的四个评价组客观独立地进行打分，给出四组评价数据组。由综合认定专家组确定朋辈评价、学院评价、教师评价和第四方专家组的比值，这四项评价值分别由B1、B2、B3与B4表示，该比值为B1∶B2∶B3∶B4，根据比值可以构建判断矩阵A=(Aij)4×4，

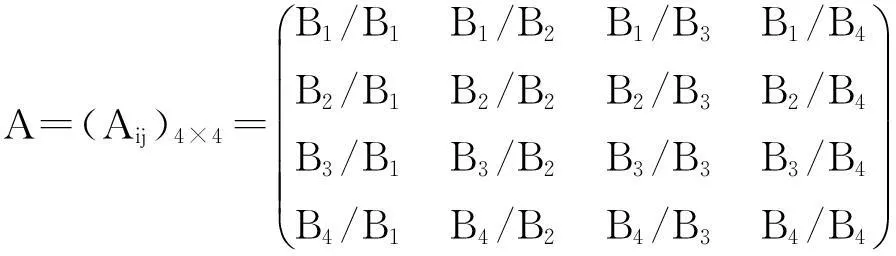
2) 计算层次单排序。根据矩阵理论，计算判断矩阵A的最大特征值λmax和对应于λmax的正规化的特征向量W。对于任何判断矩阵，均满足等式

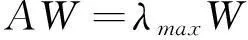
(1)

(其中λmax为A的最大特征根，W为对应于λmax的正规化的特征向量)

计算矩阵乘积AW，获得一个新矩阵，该矩阵的向量分量分别为(AW)i(其中i=1,2,…,n)。

可以得到判断矩阵的最大特征值λmax，

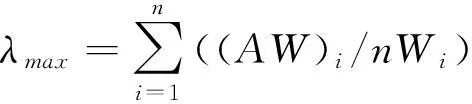
(2)

通过式(2)，便可以得到判断矩阵A的最大特征根λmax。

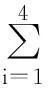
3) 矩阵一致性检验。根据矩阵理论，n阶矩阵具有唯一非零最大的特征值λmax，且λmax=n，其余特征值均为零，就可以认为该矩阵一致的。这里引进强度量相容性指标C.R.，

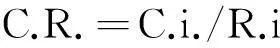
(3)

其中C.i.=(λmax-n)/(n-1)，R.i.为修正值，可以查表获得。

若C.R.<0.1，可以认为矩阵具有满意的一致性，否则矩阵不具一致性。如果矩阵不具一致性，需要重新进行两两比较判断以构建新的判断矩阵，重复一致性检验直至新的判断矩阵一致性通过。

2.2　运用熵值法计算各评价组的综合评价

1) 构建各评价组评价数据的矩阵。为了简化说明问题，这里以10名待认定学生为例，由“朋辈评价组”、“学院评价组”、“教师评价组”和“第四方专家组”分别独立地对这10名待认定学生进行评价，分别就地区状况、家庭结构、经济状况、生活状况以及学习状况等五个评价指标予以打分评价，由此可以获得朋辈评价、学院评价、教师评价和第四方专家组评价数据矩阵，分别由字母p、C、T和E表示，其中p=(pij)10×5，C=(cij)10×5，T=(tij)10×5和E=(eij)10×5。

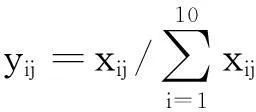
(4)

表示第j项指标下第i(i=1,2,3，…,10)个学生的指标值的比重。

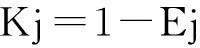
(5)

表示熵权与熵的关系。经以上计算得到权重：

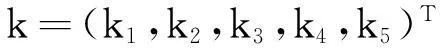
(6)

4) 计算各评价组综合评价。根据式(6)的结果，得到朋辈评价的学生综合得分

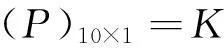
(7)

同理，可依次计算出学院评价、教师评价和第四方专家组对学生的评价数据(C)10×1，(〗T)10×1，(E)10×1。

2.3　计算困难学生认定综合评价

先将(p)10×1、(C)10×1，(T)10×1，(E)10×1合在一起可以得到新的矩阵W(2)，计算

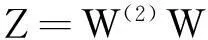
(8)

便可以得到困难学生认定综合评价向量，顺序向量Z即是最终所要得到的综合评价向量。

3应用实例

3.1　运用AHP求解评价指标的权重

1) 构建判断矩阵。根据综合认定专家组讨论研究得到朋辈评价、学院评价、教师评价和第四方专家组的比值为B1∶B2∶B3∶B4=5∶4∶6∶3。根据比值构建判断矩阵A

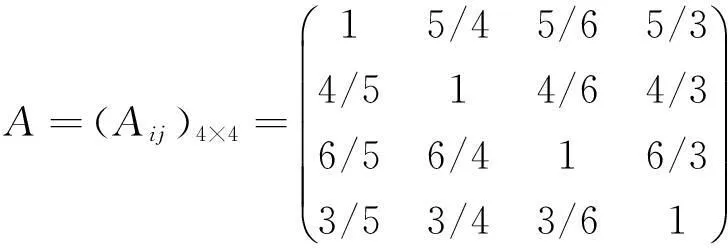
2) 最大特征值与特征向量的计算。先求判断矩阵A的最大特征值与特征向量。运用式(2)，可以得到λmax=4.000；运用式(1)，可以得到对应于λmax=4.000的正规化的特征向量为W=(0.278,0.222,0.333,0.167)T。

3) 一致性检验。CI=0.000，查表RI4=0.9，运用式(4)，可以得到CR=CI/RI=0.000<0.1，判断矩阵A一致性检验通过。

3.2　运用熵值法计算各评价组的综合评价

1) 数据处理。分别召开“朋辈评价组”、“学院评价组”、“教师评价组”和“第四方专家组”会议，根据10名待认定学生的基本情况介绍，分别就地区状况、家庭结构、经济状况、生活状况以及学习状况等五个评价指标予以打分评价，由此可以获得朋辈评价、学院评价、教师评价和第四方专家组评价数据矩阵，分别由字母p、C、T和E表示，其中p=(pij)10×5，C=(cij)10×5，T=(tij)10×5和E=(eij)10×5。收集整理的评价数据按照矩阵形式进行罗列。

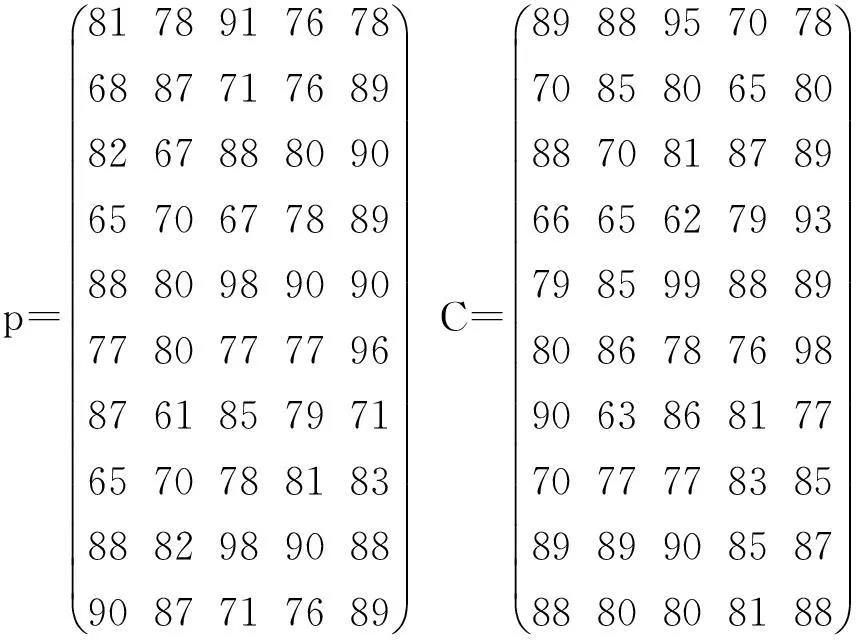
2) 计算熵和熵权。为了计算运用朋辈评价p的熵权，根据公式(4)，可以得到k1=0.003 1，k2=0.002 6，k3=0.003 7，k4=0.000 9，k5=0.001 4；根据公式(5)可以得到权重k=(k1,k2,k3,k4,k5)T=(0.267 2,0.225 8,0.314 1,0.074 1,0.118 7)T；

根据公式(7)可得朋辈(班级评议组)评价p的得分(p)10×1=(pij)10×5k。

同理依次计算出学院评价C、教师评价T和第四方专家组评价E的得分，合在一起可以得到

W(2)，W(2)=

3.3　计算困难学生认定综合评价

根据公式(8)，可以得到Z=W(2)W=(85.32,77.11,81.91,70.42,88.12,80.91,79.40,75.38,88.76,83.40)T所求Z为困难学生认定综合评价向量。

4结论

根据综合评价向量Z可知待认定学生困难程度的最终排名(如表1所示)。根据运算结果，可以基本认定S9、S5为特殊困难学生，S1、S10、S3和S6为困难学生，S7、S2、S8和S4为一般困难学生。学校可根据表1所示的困难顺序给予学生不同程度的资助。

5总结与展望

1) 实现层次分析法与熵值法的优势互补，有力地提升困难学生认定工作的科学化水平。学生的困难水平认定系统是一个多指标性、模糊性、复杂性的系统，本研究运用AHP求解评价指标的权重，恰到好处地运用了AHP主观赋权的优势，运用熵值法计算各评价组的综合评价，合理地运用了数据间内在规律给予的权重，因此使用主观赋权和客观赋权相结合的方法，有力提高认定结果的准确性，因此运

用AHP与熵值法相结合的方法是适合于困难学生认定工作的最佳方案。

2) 本研究方案是对笔者已有研究成果的优化，在一定程度上实现困难学生认定方案上的创新性。本研究使用的数据均是之前调查研究收集获得，与笔者在研究成果文献[5]中使用的同一组采集数据。换句话说，本研究方案是研究成果文献[5]的所展示方案的优化方案，是原有方案的创新成果。

3) 本研究给出一个困难学生认定优化方案模型，数据处理、计算量较大。如果运用软件工程基本方法设计成软件，一方面可以提高计算效率，另一方面友好软件界面加大推广价值。

4) 学生资助领域的研究还需要进一步深入。关于学生资助工作领域的研究系统化程度整体偏低，还有很多的薄弱之处还未进一步深入研究，如在经济资助基础上实施育人工作，学生资助与学生思想政治教育的对接研究，在注重心理安抚的前提下实施经济资助，针对困难学生群体实施心理危机干预等等。与学生资助有关的工作需要从业者在实践中创新，以学生资助为核心的领域需要更多的教育工作者深入研究。

参考文献：

[1]任海华.论高校助困现状与高校学生资助体系的构建与实践[J].吕梁教育学院学报，2009(1): 49-50.

[2]任海华，王鑫明，陆小峰，等.运用系统工程理论构建高职学生资助体系[J].温州职业技术学院学报，2013(2): 24-27.

[3]任海华.论高职院校资助育人工作新范式[J].常州信息职业技术学院学报，2014(2): 64-67.

[4]任海华，王鑫明，陆小峰，等.高职院校困难学生心理危机干预体系的构建[J].温州职业技术学院学报，2014(2): 28-32.

[5]任海华，王鑫明，陆小峰，等.基于熵值分析模型的高职院校困难学生认定[J].南通职业大学学报，2013(1): 59-62.

[6]任海华，王鑫明，陆小峰，等.基于Fuzzy-AHP的高职院校困难学生的认定[J].南通航运职业技术学院学报，2013(1): 92-95.

[7]谢乃明，刘思峰.灰色层次分析法及其定位求解[J].江南大学学报：自然科学版，2004(1): 87-89.

[8]宋海洲.群组决策的综合判断矩阵及一致性调整[J].数学的实践与认识，2010(6): 52-59.

[9]任海华.基于灰色系统层次分析的高校学生组织发展最优决策分析研究[J].南通航运职业技术学院学报，2011(1): 104-107.

[10]任海华.模糊评价方法在高职院校“推优”素质评价中的应用[J].四川职业技术学院学报，2011(3): 107-108.

[11]任海华，王鑫明，陆小峰，等.高职院校困难学生困难类别(等级)的甄别[J].温州职业技术学院学报，2013(4): 36-38，47.

本刊启事

本刊十分重视著作权、专利权的保护和保密法规的执行。由于本刊为中国期刊全文数据库收录期刊、中国学术期刊综合评价数据库统计源期刊、中文科技期刊数据库收录期刊、中国核心期刊(遴选)数据库收录期刊等，作者若不同意自己的论文被这些数据库收录，请投稿时向编辑部书面说明。

Identification of Needy Students: Analysis

Based on AHP and Entropy Method

REN Hai-hua

(Foreign Language Department, Nantong Vocational College, Nantong 226007, China)

Abstract：The identification of needy students is an essential element in implementing the national policy of student financial aid in colleges, which influences the validity of student financial aid. Based on analyzing each evaluation method, this paper uses AHP to solve the evaluation index weight; uses entropy method to calculate each evaluation group's comprehensive evaluation. With AHP and entropy method, the identification accuracy could be greatly improved.

Key words：needy students; AHP; entropy method

中图分类号：G 645.5

文献标志码：A

文章编号：1672-2434(2015)01-0031-05

作者简介：任海华(1980-)，男，讲师，主要研究方向：学生思想政治、学生资助体系构建

基金项目：江苏省教育厅2012年度高校哲学社会科学研究指导项目(2012SJDFDY117)

收稿日期：2014-05-19