基于预测的PHEV动力分配模糊逻辑控制策略

金　燕，解振方，陈佳彬，陈尔言

(浙江工业大学 信息工程学院，浙江 杭州 310023)

基于预测的PHEV动力分配模糊逻辑控制策略

金燕，解振方，陈佳彬，陈尔言

(浙江工业大学 信息工程学院，浙江 杭州 310023)

摘要：汽车运行工况对并联混合动力汽车燃油经济性具有重要影响，在用马尔科夫预测方法预测并联混合动力汽车在未来一定时间内的运行状态的基础上，提出根据预测出的状态利用模糊逻辑控制策略,来实现发动机和电机之间的最优转矩分配，使发动机工作在最佳工作点，电池SOC值保持在预期范围内.该策略克服了动态规划等全局最优控制策略需要预知全程路况信息的缺点，具有很好的实时性和鲁棒性.Advisor仿真结果表明：该方法和传统的模糊逻辑控制策略和逻辑门限控制策略相比,能更好地改善汽车燃油经济性.

关键词：马尔科夫预测；模糊逻辑控制器；Advisor；燃油经济性

中图分类号：TP18

文献标志码：A

文章编号：1006-4303(2015)01-0097-06

PHEV power distribution fuzzy logic control strategy based on prediction

JIN Yan, XIE Zhenfang, CHEN Jiabin, CHEN Eryan

(College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:Driving cycles have a significant influence on fuel economy of parallel hybrid electric vehicles(PHEV). In this paper, a method is put forward based on Markov prediction for parallel hybrid electric vehicles’ future driving cycles. According to the predicted results, a fuzzy logic strategy is used to achieve optimal torque distribution between the engine and the motor, making the engine work at optimal operating point, and keep the value of battery SOC within the expected range. According to rolling optimization features of predictive control strategy, the control strategy presented here overcomes the shortcomings of the global optimal control strategy which needs to predict the full traffic information and thus has a good real-time performance and robustness. Advisor simulation software was used to analyze the performances of hybrid vehicles by using this control strategy and existing typical control strategies respectively. The simulation results show this control strategy improves vehicle fuel economy compared to the existing typical fuzzy logic control strategy and logic threshold control strategy.

Keywords:Markov prediction; fuzzy logic controller; Advisor; fuel economy

为提高石油等不可再生能源的使用效率，以及减少汽车尾气污染物的排放，混合动力汽车作为传统汽车向纯电动汽车的过度车型越来越受到人们重视[1].如何提高混合动力汽车的燃油经济性，是人们现在面临的主要问题.混合动力汽车的动力分配控制策略一般分为基于规则和基于最优理论两大类，基于规则的控制策略有逻辑门限控制策略和模糊逻辑控制策略等[2].基于规则的控制策略控制简单，容易实现，适用性强，但不能适应工况的动态变化，无法保证车辆燃油经济性最优[3].基于最优理论的控制策略有动态规划(Dynamic programming,DP)[4]、模型预测控制(Model predictive control,MPC)[5]、等效油耗最小控制策略(Equivalent consumption minimisation strategy,ECMS)[6]等.最优理论控制策略实现了真正意义上的最优化，但计算量大，动态规划方法需要预知整个路况的信息[7]，所以该方法实现困难，难以普及.近年来，国内外研究者发现，不同的汽车行驶工况对混合动力汽车的性能影响很大[8].如果能预测出汽车未来的运行的状态，并根据未来的状态对汽车的控制策略做出调整，将会很大提高汽车的经济性能.根据汽车运行工况的随机性，提出用马尔科夫预测模型[9]对汽车未来一定时间内的状态进行预测，并根据预测的结果调整模糊逻辑控制器的控制规则，使发动机的输出转矩尽量在发动机最优转矩附近，电池的荷电状态(State of charge, SOC)维持在充放电效率最高的区域内.最后，在Advisor2002仿真软件中将该控制策略模块嵌入到某并联混合动力汽车模型中进行仿真.

1马尔科夫预测原理

马尔科夫预测过程的特性是系统在时刻t0所处的状态为已知的条件下，过程在时刻t>t0所处状态的条件分布与过程在时刻t0之前所处的状态无关.设随机过程{Zm,Tn},条件概率满足

P{Tn+1=Zm+1|T0=Z0,T1=Z1,…,Tn=Zn}

=P{Tn+1=Zm+1|Tn=Zn}

(1)

则称{Zm,Tn}为马尔可夫链[10]，马尔可夫链是状态、时间都是离散量的马尔可夫过程，其中Tn(n=0,1,2，…)为离散的时间集合，Zm(m=0,1,2，…,i,j，…)为对应的状态空间集合.条件概率为

Pij=P{Tn+1=Zj|Tn=Zi}

(2)

称为马尔可夫链{Zm,Tn}在时刻n的一步转移概率，简称为转移概率.式(2)中Zi，Zj为不同时刻的状态.式(2)表示如果系统在n时刻为状态Zi，则在下一时刻，即n+1时刻为状态Zj的概率.由不同状态的转移概率所组成的的矩阵称为马尔可夫链的一步状态转移概率矩阵P，其表达式为

(3)

马尔科夫预测的原理就是根据当前状态和状态转移概率矩阵来预测出未来某一刻的状态.其具体的方法是假设某系统的状态集为Z={Z1,Z2,…,Zm},Pij表示系统在状态Zi一次转移到状态Zj的概率.如果当前状态为Zi，根据一步状态转移概率矩阵，若

Pij=max{Pi1Pi2…Pim}

(4)

则Zj为预测到的下一时刻的状态.

2用马尔科夫预测混合动力汽车未来运行状态

根据马尔科夫预测方法的特性，将其运用到预测混合动力汽车未来运行状态是可行的，其可行性已有研究者对其进行了验证[11].该研究者者通过对汽车在CYC_UDDS工况下的不同间隔时间段的工况相关性进行分析，发现间隔时间越短，工况相关性越大，间隔时间越长，工况相关性越小，从而证明了汽车在CYC_UDDS工况中下一时刻的运行状态仅与当前时刻运行状态有关，而与之前汽车的运行状态无关，符合马尔科夫的定义.在用马尔科夫进行预测前，需要对预测对象的状态进行划分.混合动力汽车是由发动机和电机(电池供电)两种动力源进行驱动的，所以混合动力汽车的运行状态一般分为车辆停止运行(记为状态Z1)、发动机给电池充电(记为状态Z2)、发动机独立驱动(记为状态Z3)、电机独立驱动(记为状态Z4)、发动机和电机联合驱动(记为状态Z5)和车辆制动时发动机通过电机给电池充电(记为状态Z6)等6个状态[12].混合动力汽车运行状态是根据汽车的发动机输出转矩、电机的输出转矩和汽车的需求转矩来划分的，划分方法如表1所示.

表1　混合动力汽车状态表

汽车运行状态划分好后，根据前面所述的马尔科夫预测原理可求各状态间的转移概率Pij为

(5)

式中：Cij为系统在t时刻由状态Zi(i=1,2,…,5)转向t+1时刻状态Zj(j=1,2,…,5)的频率；Ci为系统的中出现Zi的总频率.例如，设发动机独立提供驱动力为状态Z1，电机独立提供驱动力为状态Z2.P12表示在某一时刻t为状态Z1且下一时刻t+1为状态Z2出现的次数除以总共出现状态Z1的次数，即状态Z1转移到状态Z2的概率.由此可求出其它状态的转移概率，进而可求得一步状态转移概率矩阵为

(6)

根据一步状态转移概率矩阵和当前的状态便可求出未来预测时间内的状态，设当前状态为1，若

P1j=max{P11P12P13P14P15}

(7)

则状态Zj={j=1,2,…,5}为下一时刻混合动力汽车的状态.在Matlab/Simulink中，用S-Function函数编写马尔科夫预测程序，在仿真开始时刻首先生成一步状态转移概率矩阵，图1为当前状态为1时的一步状态转移概率的预测模型.

图1　当前状态为1时的状态转移求解模型Fig.1　State transition model for solving when state 1

随着时间的增加，一步状态转移概率矩阵不断的更新，且转移概率矩阵都是从汽车起始运行时刻开始计算的，所以转移概率矩阵会逐步趋于稳定.预测到的汽车未来状态每K(K=1,2,3,…,n)秒周期性输出.根据预测到的结果可对下面的模糊逻辑规则作出调整，如当预测到未来K秒内状态多为电机驱动汽车或者发动机与电机联合驱动汽车时，就要保证K秒后电池有足够的电量，则当前时刻就要多使用发动机驱动汽车.若当预测到未来K秒内状态多为发动机独立提供驱动力并同时向电池充电或者制动时电机充当发电机给电池充电时，则当前时刻就要多使用电机驱动汽车，以保证电池电量始终维持在预期范围内.

3模糊逻辑控制策略

3.1模糊逻辑控制原理

模糊控制的过程主要有三个主要步骤：模糊化过程、模糊推理、反模糊化计算.模糊化过程是将输入的确定变量转换成模糊量.模糊推理是将转换后的模糊量按照一定的模糊语言规则推出一个新的近似模糊判断结论.反模糊化计算是将模糊推理得到的结论变换成确定量输出[13].选择双轴并联混合动力汽车作为研究对象，其动力总成结构示意图如图2所示.

图2　并联式混合动力汽车结构Fig.2　Parallel hybrid electric vehicle structure

根据模糊逻辑控制基本原理，制定相应的模糊控制规则，优化发动机的输出转矩和电池SOC值.利用马尔科夫预测方法预测到汽车未来运行状态后进一步合理分配发动机和电机的转矩，使汽车在满足整车需求转矩的情况下，减小电池SOC值的波动幅度.

3.2模糊控制器的设计

图3为在Simulink环境中搭建的模糊逻辑控制策略模块图，其中模糊逻辑控制模块的四个输入分别为汽车未来K秒内状态、整车需求转矩F、整车需求转矩与发动机最优输出转矩差ΔT和电池SOC值，输出为发动机输出转矩的调整系数Tw.发动机的最优转矩是根据需求转速利用插值法获得的.然后根据4个输入值制定相应的模糊控制规则.若调整后的发动机输出转矩大于整车的需求转矩，则多余的转矩驱动发电机给电池充电.反之，不足的转矩由电机提供[14].

图3　Simulink环境下的模糊逻辑控制策略模块图Fig.3　Fuzzy logic control strategy module figure in simulink environmrnt

整车需求转矩F的取值为零或非零两种状态.转矩差ΔT的模糊范围为{T1,T2,T3,T4,T5,T6,T7,T8,T9}，论域为[-80,20],隶属度函数如图4所示.电池SOC的模糊范围为{S1,S2,S3,S4,S5},论域为[0,1]，隶属度函数如图5所示.汽车未来K时刻内的状态取单值{Z1,Z2,Z3,Z4,Z5,Z6},其对应的值分别为[1,2,3,4,5,6]，其中状态1为车辆停止运行，状态2为发动机给电池充电，状态3为发动机独立驱动，状态4为电机独立驱动，状态5为发动机和电机联合驱动，状态6为车辆制动时发动机通过电机给电池充电.发动机输出转矩的调整系数Tw的模糊范围为{K1,K2,K3,K4,K5,K6,K7,K8,K9,K10,K11,K12}，论域为[0,1]，隶属度函数如图6所示.

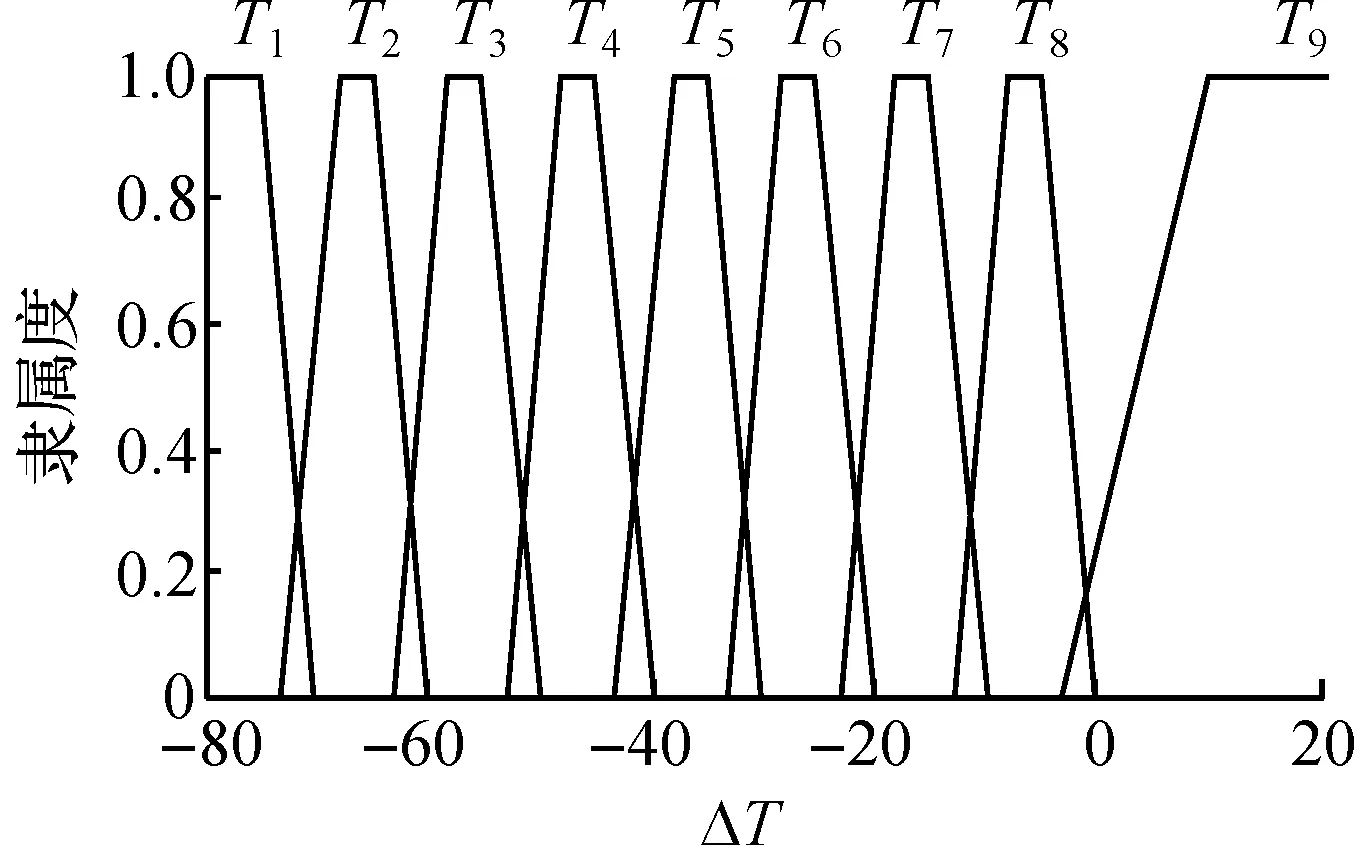
图4　转矩差ΔT的隶属度函数Fig.4　The membership function of torque difference ΔT

图5　电池SOC的隶属度函数Fig.5　The membership function of SOC

图6　调整系数Tw的隶属度函数Fig.6　The membership function of adjustment factor Tw

输入语言变量和输出语言变量均采用梯形和三角形的隶属度函数，此种隶属度函数运算简单，方便调整参数.模糊控制器的核心部分是模糊控制规则的制定，模糊控制规则的基本格式为：If输入变量1的状态and输入变量2的状态andthen输出变量的模糊状态.在此模糊控制器中与运算采用最小法，去模糊化运算采用区域重心法等.所制定的模糊控制规则如下，由于控制规则比较多,所以只列出了部分规则.

IfFis0andSOCisS3thenTwisK1

IfFis0andSOCisS2and未来状态isZ2thenTwisK5

IfFisnot0andΔTisT1andSOCisS1and未来状态isZ1thenTwisK6

IfFisnot0andΔTisT1andSOCisS1and未来状态isZ2thenTwisK9

IfFisnot0andΔTisT1andSOCisS4and未来状态isZ2thenTwisK6

IfFisnot0andΔTisT1andSOCisS5and未来状态isZ1thenTwisK1

IfFisnot0andΔTisT1andSOCisS5and未来状态isZ2thenTwisK3

……

IfFisnot0andΔTisT9andSOCisS1and未来状态isZ1thenTwisK11

IfFisnot0andΔTisT9andSOCisS5and未来状态isZ5thenTwisK8

控制规则的主要方法：

1) 若需求转矩F为零，则汽车可能处于停止或制动状态，若电池SOC值很低，并且未来K时刻需要电机提供更多的驱动力，则发动机应输出一部分转矩给电池充电，以保证未来电机的正常工作.若电池的SOC值在正常或者偏高范围内，无论未来汽车处于什么状态，发动机输出转矩为零.

2) 在需求转矩F为非零状态下，判断需求转矩与发动机输出转矩差ΔT的状态，若转矩差ΔT很小，即汽车不需要很大的驱动力，电池SOC值很高，未来K时刻内的状态以发动机驱动为主时，为使发动机工作在高效率区，此刻关闭发动机，仅以电机驱动汽车，若未来K时刻需要电机提供更多的驱动力，则发动机应输出一部分转矩给电池充电.若电池SOC值很低或者在正常范围内时，且未来K时刻内需要电机提供驱动力时，则相应的调整发动机的输出转矩，保持电池在预期的范围内，并在需要电机提供驱动力时有足够的电量供给电机，若未来K时刻内的状态以发动机驱动为主时，则此刻关闭发动机.

3) 若转矩差ΔT很大，即汽车需要很大的驱动力，若电池SOC值很高，未来K时刻内的状态以发动机驱动为主时，此时保持发动机工作在高效率区即可.若未来K时刻需要电机提供更多的驱动力，此刻除了要保持发动机工作在高效率区，还要保证电池有足够的电量，以满足未来电机的驱动.若电池SOC值很低或者在正常范围内，未来K时刻内的状态以发动机驱动为主时，此时车辆的需求转矩由发动机提供，不必向电池提供额外的转矩.若未来K时刻需要电机提供更多的驱动力，则发动机除了要满足车辆的需求转矩外还要向电池充电，以满足未来电机有足够的驱动力驱动车辆.

4) 如需求转矩与发动机输出转矩差ΔT为零或大于零，表示整车的需求转矩等于或大于发动机的最优转矩，此时应使发动机工作在最优转矩范围内，剩余的转矩由电机的输出转矩提供，若此时电池的SOC值很高，无论未来K时刻车辆处于什么运行状态，保持发动机最优输出转矩不变.若此时电池的SOC值很低，无论未来K时刻车辆处于什么运行状态，应少量增大发动机的输出转矩，保持电池在预期的范围内.

5) 上述仅仅部分主要的控制规则，将输入输出的模糊范围划分多个区域，是为了提高控制规则的细化程度，根据不同的状况使发动机的输出转矩有更多的选择，进而提高汽车整体经济性能.

4仿真分析

为了验证所设计的控制策略的有效性，在Matlab/Simulink软件中搭建马尔科夫预测模块和模糊逻辑控制模块，并将其嵌入到Advisor2002仿真软件中进行仿真.选取双轴并联式混合动力汽车模型作为仿真车型，主要的仿真参数见表2.汽车的行驶工况选择典型的CYC_UDDS工况.

表2　主要部件的仿真参数

图7　三种控制策略下的SOC值Fig.7　The SOC of three control strategies

图8　CYC_UDDS工况下预测汽车运行状态的各种数据输出图Fig.8　Predict HEV various data output figure under the CYC_UDDS condition

图7为三种控制策略仿真后的电池SOC的变化曲线图.其中传统模糊逻辑控制策略是指不考虑汽车未来状态，仅以整车需求转矩、整车需求转矩差与发动机最优转矩差和电池SOC值作为输入变量的模糊控制策略.图中的横坐标表示时间，纵坐标表示电池的SOC值.三种控制策略的SOC值的初始值都为0.7，都最终降到0.63左右，表明电池在三种控制策略下的消耗量都是相同的，且都使电池SOC值保持在高充放电效率范围内.图8为在CYC_UDDS工况下预测汽车运行状态各种数据输出图，其中图8(a)为在整个CYC_UDDS工况下车辆的电机输出转矩曲线图，图8(b)为在该工况下的发动机输出转矩曲线图，图8(c)为车辆的需求转矩曲线图，图8(a,b,c)中的横坐标表示时间，纵坐标表示转矩值.图8(d)为在CYC_UDDS工况下马尔科夫预测出的汽车未来状态图.图8(e)为在CYC_UDDS工况下基于逻辑门限控制策略下的汽车运行状态图.图8(d,e)中的横坐标表示时间，纵坐标表示汽车运行状态.根据马尔科夫预测原理滚动优化的特点，从图8(d,e)可以看出：在整个工况前400 s两种状态相差比较大，但随着时间的增加，马尔科夫预测出的状态逐渐趋近基于逻辑门限控制策略下的汽车运行状态.通过对图8的观察，采用马尔科夫预测理论来预测汽车未来状态的方法基本符合表1中对混合动力汽车未来状态的划分.

CYC_UDDS工况下3种控制策略的百公里燃油消耗量的仿真结果见表3,从表3中可以看出：马尔科夫预测结合模糊逻辑控制策略相比逻辑门限控制策略将汽车的百公里燃油消耗减少了17.2%，相比于传统模糊逻辑控制策略减少了2%.在电池消耗量相同的情况下，燃油消耗的减少说明了采用马尔科夫预测与模糊逻辑控制相结合的控制策略的有效性和提高了汽车燃油经济性.

为验证所设计的控制策略能够适用于多种工况下，又分别选择CYC_WVUSUB，CYC_NurembergR36和CYC_MANHATTAN三种工况进行仿真，仿真结果见表3.从表3中可以看出：在这三种工况下，马尔科夫预测结合模糊逻辑控制策略的百公里燃油消耗量都少于另外两种控制策略，从而验证了马尔科夫预测结合模糊逻辑控制策略适用于多种工况.

表3三种控制策略分别在三种不同工况下的百公里燃油消耗量

Table 3The fuel consumption under the different control strategy and condition

工况百公里燃油消耗量/L马尔科夫模糊逻辑逻辑门限SOCCYC_UDDSCYC_WVUSUBCYC_NurembergR36CYC_MANHATTAN4.85.38.19.44.95.48.39.75.86.28.910.70.630.620.650.65

5结论

运用马尔科夫预测理论预测汽车未来一定时间段内汽车的运行的状态，并与汽车的需求转矩、车辆需求转矩与发动机转矩差和电池的SOC作为模糊逻辑控制器的输入变量，通过制定相应的模糊逻辑控制策略，提高了汽车的燃油效率.模糊逻辑控制策略实现了发动机和电机之间转矩合理分配，并使电池的SOC值始终保持在高充放电效率范围内.根据仿真结果也证明了运用马尔科夫预测理论来预测汽车未来运行状态的可行性.

参考文献：

[1]肖湘宁,陈征,刘念.可再生能源与电动汽车充放电设施在微电网中的集成模式与关键问题[J].电工技术学报,2013，28(2)：1-14.

[2]SANJAKA G W, ALI E. Classification and review of control strategies for plug-in hybrid electric vehicles [J]. IEEE Transactions on Vehicular Technology,2011,60(1):111-122.

[3]YANG Lianghui, HE Hongwen, SUN Fengchun, et al. Research of fuzzy logic control strategy for engine start/stop in dual-clutch hybrid electric vehicle[J]. Seventh International Conference on Fuzzy Systems and Knowledge Discovery,2010,6(8):912-917.

[4]肖仁鑫,李涛,邹敢,等.基于随机动态规划的混联式混合动力汽车能量管理策略[J].汽车工程,2013,35(4):317-322.

[5]舒红,郑军,胡明辉,等.基于模型预测控制的混合动力汽车下坡再生制动策略[J].汽车工程,2013,35(9):775-780.

[6]GENG B, JAMESK M, SUN D. Energy management control of microturbine-powered plug-in hybrid electric vehicles using the telemetry equivalent consumption minimization strategy[J]. IEEE Transactions on Vehicular Technology,2011,60(9):4238-4248.

[7]张炳力,张平平,赵韩,等.基于离散动态规划的PHEV燃油经济性全局最优控制水[J].汽车工程,2010,32(11):923-927.

[8]田毅,张欣,张昕,等.计及行驶工况影响的混合动力汽车控制策略[J].汽车工程,2010,32(8):659-663.

[9]周勇有.基于马尔科夫预测的混合动力汽车控制策略:[D].吉林:吉林大学,2009.

[10]叶圣永,王晓茹,周曙,等.基于马尔可夫链蒙特卡罗方法的电力系统暂态稳定概率评估[J].电工技术学报,2012,27(6):168-174.

[11]张岩.面向混合动力汽车能量管理策略的汽车运行工况多尺度预测方法[D].吉林:吉林大学,2013.

[12]倪成群,赵强,张幽彤.插电式混合动力客车电能消耗阶段控制策略的研究[J].汽车工程,2014,36(1):12-16.

[13]曾国伟，赵国军，邢海潇，等.基于模糊控制技术的电梯群控系统设计[J].浙江工业大学学报，2009,37(1):115-118.

[14]WU Jian, ZHANG Chunheng, CUI Ningxia. Fuzzy energy management strategy for a hybrid electric vehicle based on driving cycle recognition[J]. International Journal of Automotive Technology,2012,13(7):1159-1167.

(责任编辑：刘岩)

作者简介：金燕(1964—)，女，浙江绍兴人，副教授，研究方向为自动化检测和控制、混合动力汽车控制策略等，E-mail:jya@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(61273116)

收稿日期：2014-09-30