一个随集团规模改变的集团部分分解羊群模型

2015-02-19周明华郑婷婷

浙江工业大学学报 2015年1期

关键词：模拟经纪人收益率

周明华，陆　川，俞　伟，郑婷婷

(浙江工业大学理学院, 浙江杭州 310023)

一个随集团规模改变的集团部分分解羊群模型

周明华，陆川，俞伟，郑婷婷

(浙江工业大学理学院, 浙江杭州 310023)

摘要：在EZ羊群模型的基础之上,提出了一个随集团规模改变的集团部分分解羊群模型.该模型认为,在现实的金融市场中，由于集团内各个交易者所获得的信息，他们的期望值和心理因素等有差异，同属一个集团的经纪人中，并非所有人都采取相同的策略，同一集团内参与交易的人数与所在集团的规模大小有关.通过大量的数值计算，我们发现，该模型产生了收益率的尖峰胖尾分布，这说明其能较好地反映金融市场的动力学行为和特性.

关键词：羊群模型；经纪人；收益率；部分分解；集团规模；模拟

中图分类号：F224.32

文献标志码：A

文章编号：1006-4303(2015)01-0115-04

A cluster-partial-separation herding model with change of cluster size

ZHOU Minghua, LU Chuan, YU Wei, ZHENG Tingting

(College of Science, Zhejiang University of Technology, Hangzhou 310023, China)

Abstract:In this paper, we propose a cluster-partial-separation herding model with change of cluster size based on EZ herding model. In this model, according to the real financial market, different agents in a cluster may have different knowledge, different expectations and different mental states about the sharing information, not everyone will take the same strategy. Number of persons involved in the transaction is related with the size of cluster. The numerical calculation shows this model produces peak fat-fail distribution of yields. This shows that it can better reflect the dynamic behavior and characteristics of the financial markets.

Keywords:herding model；agent；yields；partial separation; cluster size；simulation

近年来，随着人们对金融市场的微观结构不断深入认识，再加上行为金融学与计量经济学的蓬勃发展，相关学者开始深层次思考投资者行为[1-5]，对金融时间价格的收益率的研究是研究的热点之一[6-7]，由Eguiluz和ZimmermannEZ发表在Physical Review Letters中提出的羊群模型正是从金融市场微观机理上对收益率尖峰胖尾现象进行解释的产物[8].EZ羊群模型考虑了一个含有N个经纪人的系统，同一集团内的经纪人享有共同的信息，经纪人之间可以通过分离或合并形成集团.该模型由于其简洁性，并且产生了金融价格收益率的胖尾分布而得到了许多学者的重视.

自从羊群模型被提出后，相关的衍生模型层出不穷[9-14].在此模型的基础之上，2004年，郑波等人提出了相互作用羊群模型[9]，他们认为，真实市场信息传播的比率不应该是原始EZ羊群模型中假设的常数，而应随集团的规模的改变而改变.2006年，董林荣提出了具有长程记忆的相互作用羊群模型[10]，对羊群模型作了进一步改进.2008年和2010年，董林荣又分别提出了自适应羊群模型[11]和异质类经纪人相互作用的羊群模型[12].对于前者，他认为经纪人的市场判断力会影响他的羊群行为；而对于后者，他认为原始的羊群模型没有区分不同类型的经纪人，因此他将经纪人集团进行分类，使得模拟出来的结果更加接近真实的金融市场.2011年，余义龙提出了具有长程记忆和市场判断力的异质经纪人羊群模型[13]，在此模型中，他认为真实的金融市场应该将经纪人的记忆性和异质性同时考虑.

1随集团规模改变的集团部分分解羊群模型

在纵观对收益率尖峰胖尾分布这一程式化规律的微观机理研究之后，我们发现，目前已有的研究羊群行为的各种模型，在一定程度上反映金融市场的规律，但离真实的金融市场都还有一定的距离.这些模型都遵循了EZ羊群模型中的提出的假设之一，即同一集团的经纪人由于羊群行为会采取相同的策略，但这与现实中的某些现象不太吻合，因此，为了更贴近现实的金融市场，我们提出了随集团规模改变的集团部分分解羊群模型.

根据现实的金融市场，由于集团内各个交易者所获得的信息，他们的期望值和心理因素等有差异，同属一个集团的经纪人中，并非所有人都采取相同的策略；在规模越大的集团中，由于集团内的经纪人越多，信息量就越多，交流会越充分，故采取共同行动的人会越多，而在集团规模越小的集团中，由于信息量的缺乏，采取相同策略的经纪人就越少.正是考虑到以上的现实原因，我们修改了原始的EZ羊群模型，提出了随集团规模改变的集团部分分解羊群模型.

该模型的初始条件与EZ羊群模型一致,即在一个含有N个经纪人的系统中,经纪人l的状态用φl={0,+1,-1}表示(0表示等待，+1表示买入，―1表示卖出).初始状态下，各经纪人处于等待状态(φl=0,∀l)，此时各经纪人均是独立的(每一个经纪人构成了一个集团[8]).接下来在某一时刻t：

1) 随机选择经纪人i[8].

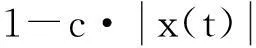
3) 经纪人i以概率(1-a)选择等待，此时，在i所在集团外随机选择经纪人j，i所在的集团与j所在的集团合并为更大的集团.

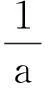
这里需要指出的是，当c=0时，说明集团内所用经纪人均跟随i进行交易，此时模型即为EZ羊群模型，可见EZ羊群模型是随集团规模改变的集团部分分解模型的一种特殊情况.

2模拟与讨论

2.1规范化收益率的幂率分布

为了检验此模型是否抓住了现实金融市场的程式化规律，我们选择对其参与交易的集团规模以及对应的规范化收益率进行进行数值模拟.在以下模拟过程开始前，为了方便起见，我们不妨将参数c和δ分别取定值为1和1/4.

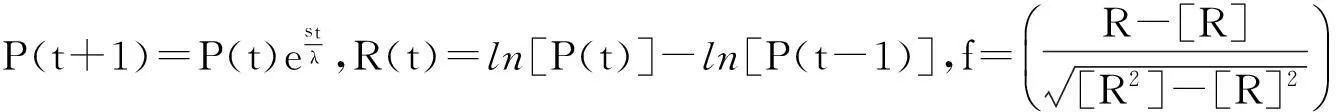
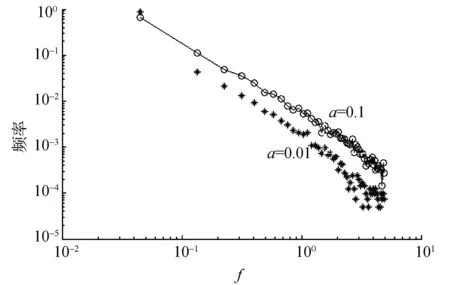
图1　规范化收益率f频率分布的双对数图Fig.1　Log-log plot of distribution of normalized return f

2.2时序图

图2所示为规范化收益率f随时间的演化图，图3则是经纪人集团随时间的演化图.从图2，3中我们可观察到：规范化收益率f出现明显的间歇性开关行为和易变集结现象，所谓易变是指规范化收益的绝对值，这些现象是经济生活中所特有的[12].比较这两张图，我们发现，当规范化收益率呈现出较大值时，也正好是经纪人集团规模较大时，这就与现实金融市场的一条经济规律相吻合，即市场大的波动是由较大的经纪人集团所产生的[12].

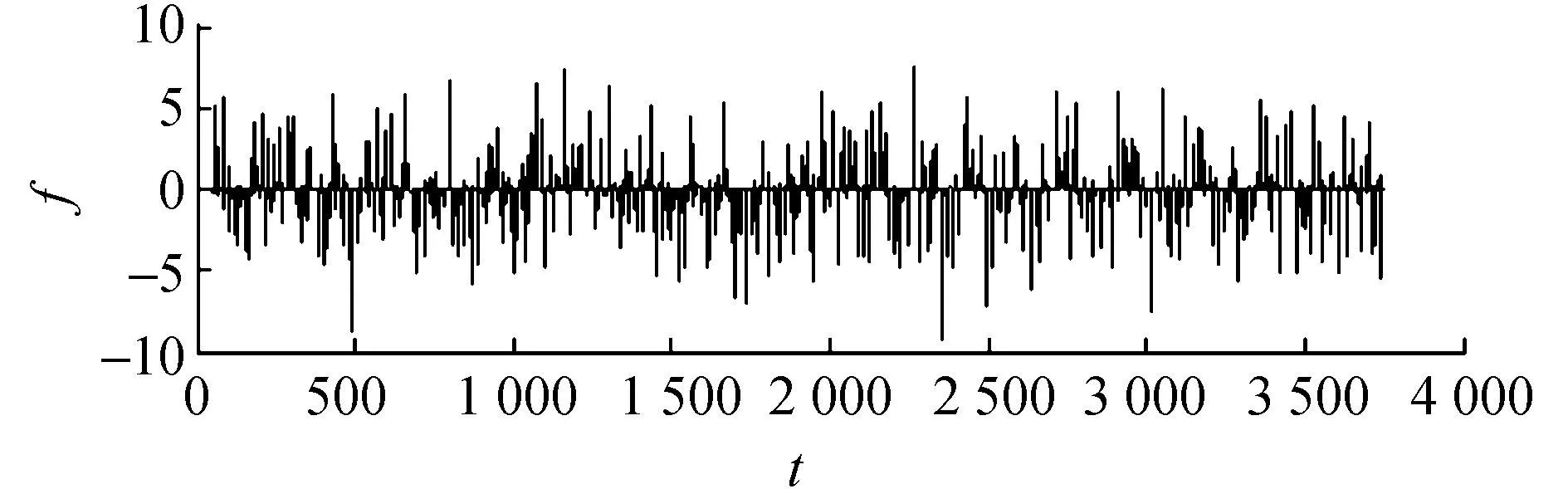
图2　规范化收益率f随时间的演化图Fig.2　Time evolution plot of normalized return f

图3　经纪人集团S随时间的演化图Fig.3　Time evolution plot of size of cluster S

2.3规范化收益率和集团规模的尖峰胖尾分布

图4显示了规范化收益率概率的线性—对数分布图，通过取相关参数N=1×104,a=0.1,T=1×106，我们可以发现收益率呈现出显著的尖峰胖尾现象，这与真实市场的程式化规律相吻合[1].考虑到实际市场的人数很有可能会更大，为此，我们扩大模型的总人数，并改变a的取值，继续考察模型的相关频率分布图.

图5中，星号线代表的是当模型中的参数分别为N=4×104,a=0.2,T=1×106时，规范化收益率的概率分布情况.考虑到现实市场中集团的信息传播速度不同，为此我们改变a的取值，得到了当a=0.3时的情形，圆圈线表示的就是此时集团规模的概率分布.我们发现，当集团规模，信息传播等相关参数改变时，由该模型所产生的集团规模仍然呈现出尖峰胖尾现象，这说明该模型能模拟一些不同市场的动力学特征.

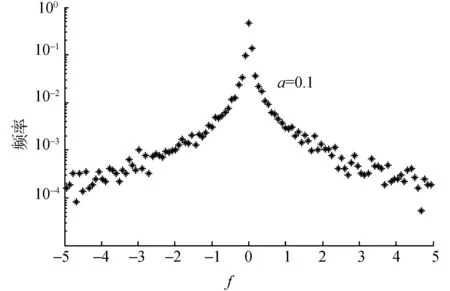
图4　规范化收益率f频率分布的线性-对数图Fig.4　linear-log plot of distribution of normalized returnf

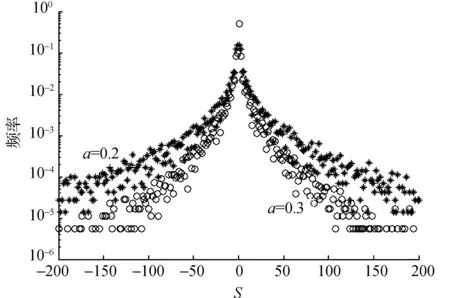
图5　集团规模S频率分布的线性-对数图Fig.5　linear-log plot of distribution of size of clusters S

3结论

一个随集团规模改变的集团部分分解羊群模型认为，由于集团内各个交易者所获得的信息，他们的期望值和心理因素等有差异，同属一个集团的经纪人中，并非所有人都采取相同的策略，而是采取同一行动的人数与经纪人所在集团的规模成正比.该模型根据真实的金融市场，修改了EZ羊群模型及其众多衍生出来的模型有关同一集团内羊群行为的假设，因此大大丰富了模型的实际意义.由于该模型中许多参数具有调节性，而不同参数的取值代表了实际不同的市场，并且数值模拟的结果都在真实市场规律的范围内，因此该模型具有普遍的意义.

参考文献：

[1]CONT R. Empirical properties of asset returns: stylized facts and statistical issues[J]. Quantitative Finance,2001,1(2):223-236.

[2]陈多长，余巧奇，虞晓芬.城市居民租购住房偏好差异及其影响因素——以杭州市为例的实证研究[J].浙江工业大学学报,2011,39(1):1-6.

[3]CONT R, BOUCHAUD J P. Herd behavior and aggregate fluctuations in financial markets[J]. Macroeconomic Dynamics,2000,4:170-196.

[4]RODGERS G J, ZHENG D F. A herding model with preferential attachment and fragmentation[J]. Physica A,2002,308(2):176.

[5]ZHENG D F, RODGERS G J, HUI P M, et al. Non-universal scaling and dynamical feedback in generalized models of financial markets[J]. Physica A,2002,303(2):180.

[6]LUX T. The socio-economic dynamics of speculative markets: Interacting agents, chaos, and the fat tails of return distributions[J]. Journal of Economic Behavior and Organization,1998,33(2):1235-1274.

[7]LUX T. Power laws and long memory[J]. Quantitative Finance,2001,1(6):621-631.

[8]EGUILUZ V M, ZIMMERMANN M G. Transmission of information and herd behavior: an application to financial markets[J]. Physical Review Letters,2000,85(2):183.

[9]ZHENG B, REN F, TRIMPER S, et al. A generalized dynamic herding model with feed-back interactions[J]. Physica A,2004,343(2):653-661.

[10]DONG Linrong. Interacting herding model: memory and oblivion[J]. Acta Physica Sinica,2006,55(8):4046-4050.

[11]DONG Linrong. A self-adapting herding model: the agent judge-abilities influence the dynamic behaviors[J]. Physica A,2008,387(2):185.

[12]DONG Linrong. A heterogeneous agent herding model with dual feedback interactions[J].Journal of Zhejiang University,2010,37(1):46-50.

[13]余义龙，成丹丹，周明华，等.具有长程记忆和市场判断力的异质经纪人Herding模型[J].浙江工业大学学报,2011,39(2):231-236.

[14]JIRI K, JOZEF B. Behavioural breaks in the heterogeneous agent model: the impact of herding, overconfidence and market sentiment[J]. Physica A,2013,392:5920-5938.

(责任编辑：刘岩)