多车型同时取送货问题的低碳路径研究

赵燕伟,李　文,张景玲,任设东

(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014)

多车型同时取送货问题的低碳路径研究

赵燕伟,李文,张景玲,任设东

(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014)

摘要：针对现代物流配送系统中提倡节能减排、配送中心多车型、车辆数量有限以及客户存在取送货需求的特点，建立了多车型同时取送货的低碳路径问题的模型，同时建立了考虑车辆装载量、车型和距离的碳排放量的计算方法.基于问题的性质，采用了量子进化算法对其进行求解，量子进化算法是一种通过将常用的整数编码转换成量子比特位的编码方式，每一个染色体都代表某种车型的行车路线方案，通过基准测试实例验证了算法的有效性和可行性，实验分析表明，针对多车型同时取送货问题，以总碳排放最小为目标函数，采用随机选取车辆路径安排比传统的车辆路径安排更加经济和环保.

关键词：物流；车辆路径；多车型；同时取送货；量子进化算法；碳排放

中图分类号：F224

文献标志码：A

文章编号：1006-4303(2015)01-0018-06

Low carbon for a multi-vehicle routing problem with

simultaneous pickups and deliveries

ZHAO Yanwei, LI Wen, ZHANG Jingling, RENG Shedong

(Key Laboratory of Special Purpose Equipment and Advanced Manufacturing Technology, Ministry of

Education, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:Aiming at the promotion of energy-saving for logistics, vehicles’ diversification and the customer has take and delivery requirements in the vehicle routing problem, a model that low carbon for a multi-vehicle routing problem with simultaneous pickups and deliveries was established, which put forwards the calculation of considering the loading capacity, the models and the distance for carbon emissions. Base on the nature of the problem, using the quantum evolutionary algorithm to solve it, an encoding method of converting Q-bit representation to integer representation was designed, every chromosome represented a kind of route, Some examples were tested to verify the feasibility and effectiveness of the algorithm, for the above-mentioned problems, low carbon vehicle arrangement was more economic and environmental than traditional vehicle touting arrangement.

Keywords:logistics； vehicle routing； multi-vehicle； simultaneous pickups and deliveries； quantum evolutionary algorithm； low carbon

随着现代社会的高速发展，全球环境问题逐渐受到人们的关注，温室气体的不断排放也越来越被世人所担忧，当今物流社会，物流运输产生大量的CO2排放，约占全社会排放量的30%，针对现在气候环境的不断改变，物流运输业需要改变其发展的方式，提倡和实施“绿色运输”已成为物流运输活动中重要的发展趋势.

车辆路径问题(VRP)是Dantzig与Ramser在1959年提出的，后面的学者进行了许多的研究，出现了很多重要的研究成果，研究方向主要是在单车型单需求VRP[1]方面，然而，在实际的配送中，车辆拥有多种车型，且每种车型的装载能力，单位旅行费用以及发车成本等都是各不相同的，考虑配送总资金的约束，配送中心每种车型的数量也是有限制的，客户一般可以只具有取货需求或送货需求，也可以同时具有两种需求，因此，研究多车型同时取送货VRP问题更加接近实际的配送管理.在已有的文献中，姚锦宝[2]在同时取送货车辆路径问题中用了改进的蚁群算法，建立了一个基于不确定的二级供应链的模糊规划模型；贾芳芳[3]对该问题用了改进的粒子群算法，采用惯性权重更新和路径链接更新来扩大粒子的搜索空间，对模型的收敛速度有了明显提升；刘晴[4]针对具有随机需求的同时取送货车辆路径问题进行了研究；马宇红[5]利用遗传算法研究了大规模的多配送中心多车型车辆调度问题；这些文献分别对同时取送货车辆路径问题和多车型车辆路径问题进行了研究，但却没有将两者进行结合，且目标大多只关心经济效益，没有考察CO2排放对环境造成的污染，传统VRP问题在车辆路径安排时只考虑经济成本[7]，而扩展传统VRP问题的目标就是在车辆路径安排时加入对环境影响的考虑，以有效的减少VRP问题中碳的排放量，杨培颖[13]从碳排放的角度建立了针对接送机场服务中心以车辆最新碳排放量为目标的非线性0-1混合整数规划模型；王钰青[14]建立了基于最小碳排放的广义TSP模型；邱雅君[15]通过改进的遗传算法求解了考虑碳排放因素的车辆路径问题.对多车型同时取送货问题的低碳研究，碳排放量与燃油消耗成正比例关系[12]，碳排放量的计算将考虑车型、距离、载重量等多个因素的影响；在模型算法方面，考虑到多车型与同时取送货相结合的问题建模困难，采用高效率高寻优的量子进化算法来进行求解运算.

1多车型同时取送货低碳路径问题的描述及数学规划模型

1.1问题描述

多车型同时取送货的低碳路径问题的描述为：配送中心拥有不同类型的车型，每种车型的数量有限制，配送中心分配车辆给客户服务，客户具有取货需求和送货需求，每辆车完成任务后返回配送中心且不再配送货物；目标是在满足客户取送货需求的条件下安排车辆路径使得碳排放量最小.约束为：只有一个配送中心，车辆配送结束后立即返回配送中心且不再配送服务；每个客户必须被访问且只能被访问一次；配送线路上货车的装载量至少能同时满足任意一个客户的两种需求，每种车型的车辆数固定，且具有不同的载重量和燃油消耗参数[8](与计算碳排放量有关).

1.2模型的建立

1.2.1碳排量的计算

根据不同的精度要求和所采集的数据种类，二氧化碳排放量的计算可以选取不同的计算方法.文献[8]有

F=GD(aL+b)

(1)

其中：F为货物运输过程中的燃油消耗；G为地形坡度因子；D为车辆行驶距离；L为车辆载重；a，b分别为燃油消耗参数(该参数随车型的变化而变化).

计算出车辆的燃油消耗，需要将其转化为直接碳排放量，同样根据文献[8]，有

W=Fη

(2)

其中：W为直接碳排放量；η为燃油转换系数.

根据上述方法计算车辆的二氧化碳排放量，从式(1,2)中可以看出：碳排放量和燃油消耗量成正比例关系；燃油消耗和车辆行驶距离成正比例关系；与载重量成正线性相关，同时为了验证模型有效性，取地形坡度因子G为单位1，根据实际问题可以得出

(3)

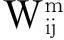
1.2.2数学模型

多车型同时取送货低碳路径问题的数学模型如下：

(4)

s.tpij+qij≤Qmxijk,∀i,j,m,k

(5)

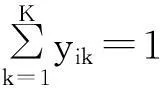
(6)

(7)

(8)

(9)

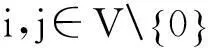
(10)

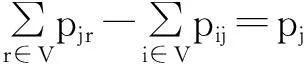
(11)

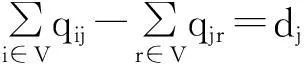
(12)

p0j=0,∀j∈V{0}

(13)

qi0=0,∀i∈V{0}

(14)

(15)

(16)

(17)

pij≥pixijk,∀i∈V{0},∀j∈V,∀k

(18)

qij≥djxijk,∀i∈V,∀j∈V{0},∀k

(19)

xijk=0或1,∀i,j,k,yik=0或1,∀i,k

(20)

其中：S=(V,E)为配送网络，V为节点集，V={0,1,…,n}，其中0表示配送中心，其余节点表示客户；E为边集，E={(i,j)|i,j∈V,i≠j}；m为车型，编号为1，2，…，M；k为车辆，编号为1，2，…，K；Qm为m类型车的容量，m∈{1,2,…,M}；pi为客户i的取货需求；dj为客户j的送货需求；nm为m类型车辆数限制；

k∈{1,2,…,K},i∈V,j∈V；

式(4)表示目标函数，为车辆的总碳排放量最小；式(5)表示车的载重不大于它的载重能力；式(6)表示每个客户都会被服务到；式(7，8)表示客户有且仅被一辆车服务；式(9)表示离开配送中心的车辆和返回配送中心的车辆数量是一致的；式(10)表示两个客户服务时线路数不能超过1；式(11)表示客户的送货需求被满足；式(12)表示客户的取货需求被满足，这两个约束同时保证了客户的取送货需求被满足；式(13)表示刚从配送中心出发的车不会取货；式(14)保证返回配送中心的车辆不再服务；式(15)保证返回配送中心的所有车辆取货总和等于所有客户的取货需求总和；式(16)表示总车辆数约束；式(17)保证所有从配送中心出发车辆装载的货物总和等于所有客户的送货需求总和；式(18)保证离开客户后车辆的取货不能小于该客户的取货需求；式(19)表示到达任一客户的车辆装载的将要派送的货物不能小于该客户的送货需求；式(20)表示变量的取值范围.

2多车型同时取送货低碳路径问题的算法设计

2.1量子进化算法的求解过程

针对第1章建立的多车型同时取送货低碳路径问题的数学规模模型，我们采用量子进化算法进行求解的策略如图1所示.

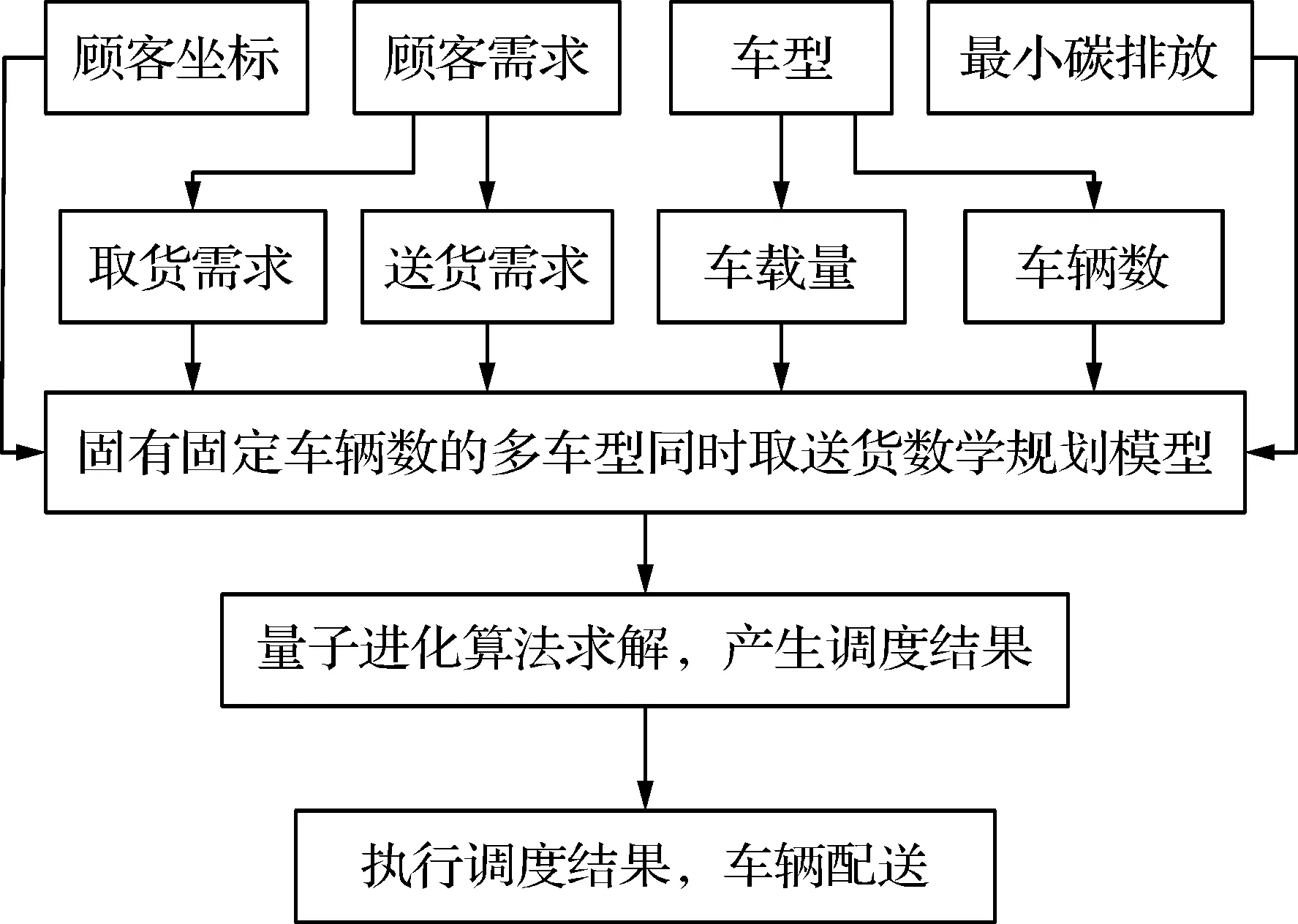
图1　多车型同时取送货低碳路径问题求解策略Fig.1　The solving strategies of the low carbon for a multi-vehicle routing problem with simultaneous pickups and deliveries

采用量子进化算法对该问题就行求解，充分利用了量子进化算法的全局寻优能力强和收敛速度快的特点，使问题可以找到比较满意的解.

2.2量子进化算法

量子染色体是量子进化算法独有的概念，采用量子比特进行编码.每个量子比特位存在|0>和|1>两个本征态，该量子比特位可以处于|0>和|1>两个本征态的任意叠加状态，一个包含m×n维矩阵的量子染色体可以表示为

(20)

其中：qij为量子比特，满足|qij>=αij|0>+βij|1>,|αij|2+|βij|2=1，|αij|2和|βij|2分别表示量子位处于|0>的概率和量子位处于的|1>概率.一个包含m×n维矩阵的量子染色体可以表示2mn个状态的叠加，这样就使得量子进化算法具有非常广泛的搜索空间.

量子进化算法的求解流程如图2所示.

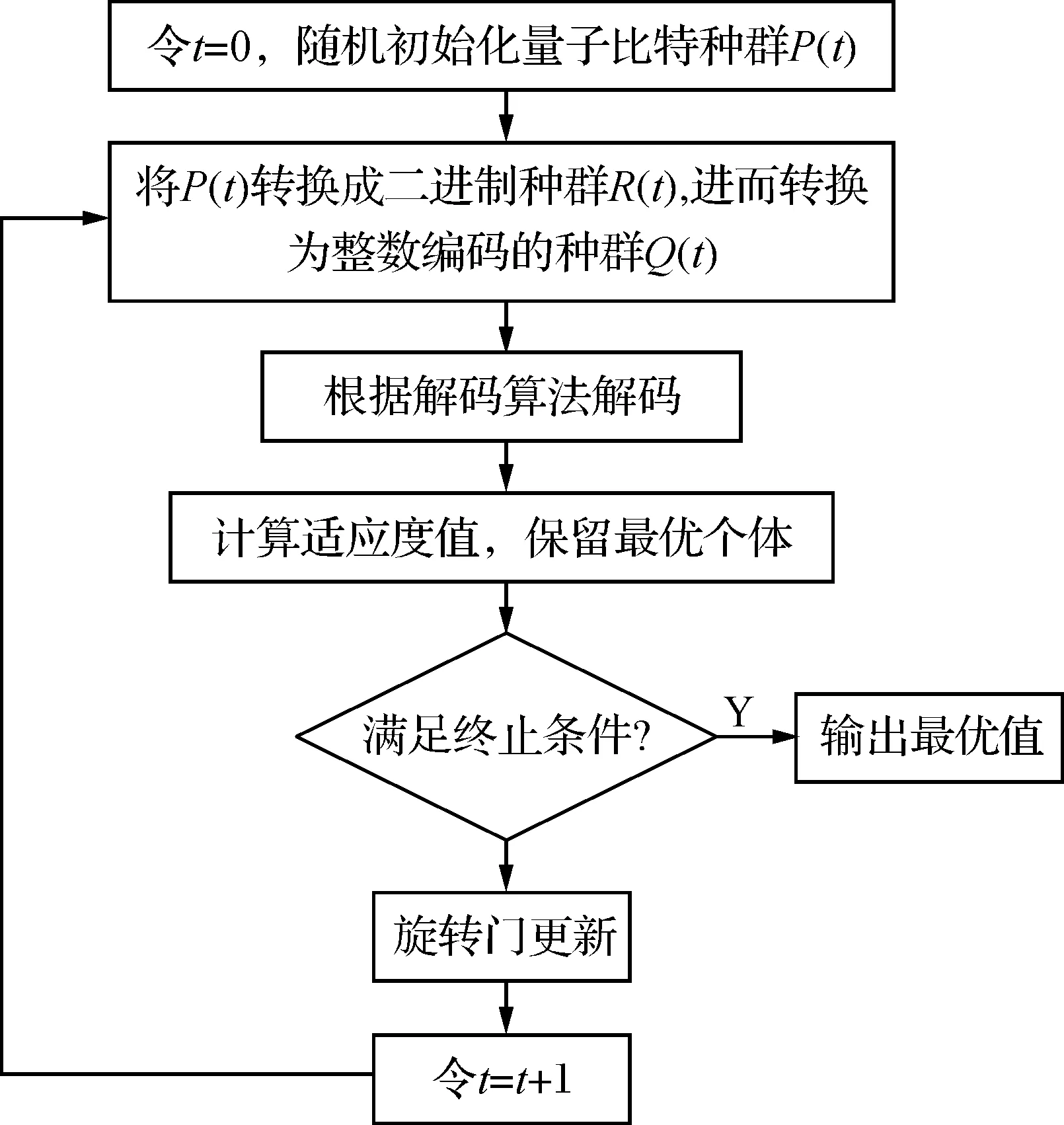
图2　量子进化算法流程图Fig.2　Quantum algorithm flow chart

算法具体的求解过程如下：

1) 初始化量子比特种群

随机产生包含多个量子染色体的种群，针对客户数量为L的问题，对于每个量子染色体，可以采用L×L×2的三维量子比特矩阵来表示，随机初始化量子比特位，由计算机随机0，1之间的随机数，然后赋值给对应的αij和βij.

2) 对量子比特种群解码

解码过程先生成客户序列，然后再进行车辆分配.

产生客户服务序列：首先产生[0,1]之间的随机数，产生L×L的二维0～1观测矩阵，并调整矩阵保证每行每列都只有1个1,1所在的横坐标代表服务的顺序，纵坐标代表所对应的的客户.例如对于配送客户数L=6的问题，经过量子塌陷得到二进制染色体P=[001000100000000010010000000001

000100]，然后对其进行分段，每段长度为L，然后根据对于横坐标所在的1确定客户服务顺序，即初始化客户服务序列为3→1→5→2→6→4.

车辆的分配：我们采用贪心算法形成路径，首先随机选用一种车型的车辆，当该车辆无法满足下一个客户需求时，我们再随机选用一种车型的车辆(每次选取车辆时是独立的，前后选取车辆的车型可能相同也可能不同)，当该种车型的车辆数超过已有车辆数时，我们重复选取车型的步骤，直到所选车型没有超过该种车型的车辆数为止.例如对于上面的客户服务序列，假设有3种类型的车型，每种车型的载重和数量各不相同，当开始随机选用车型1的车辆配送客户3和客户1后无法再配送5，这是需再随机选用某种车型进行配送，可能还是车型1或者其他车型，假设当某次随机选取到车型2的车辆配送客户5时发现车型2的车辆全部配送完，这是我们需要随机选取其他没配送完的车型来配送.

3) 适应度计算

对种群的各个染色体解码后，分别根据式(4)求得目标函数值Z；令染色体的适应度函数为ffitness=Z，由此可见：适应度函数越小，车辆配送的方案越有助于减少碳排放.

4) 量子旋转门更新

量子进化算法也有“进化”的概念，而最为常用的“进化”机构就是量子旋转门，进化过程由量子旋转门更新量子位概率幅来实现，具体参考文献[16].

3实验结果及分析

3.1实例测试

算法程序是java语言编写的，在Penti-umDCPU2.0GHz，2.0GB的内存上运行.用上述提到的算法来求解我们建立的模型，该物流系统只拥有1个配送中心，3种不同的车型，每种车型的载重量分别是150，120，100t，初始的客户总数为39个，0为配送中心，1~39为客户点，各客户点的坐标和取送货需求如表1所示.

表1　初始客户点信息

对上述数据用算法进行求解，车辆随机分配时得出最优的车辆路径分配方式如表2所示.

表2　各车型的路径分配方式

模型算法的目标函数收敛图如图3所示.

图3中分别包括车辆随机选用、优先选用碳排放系数低的车辆和优先选用碳排放系数高的车辆的目标函数收敛图.由此可以看出：当我们以碳排放最低为目标函数时，且车型以不同的方式分配，通过量子进化算法对模型进行求解，得出当车辆被随机选用时最低碳排放量排放大约为195 t左右，当优先选择碳排放量低的车型时，得出的最低碳排放量也是大约190 t左右，和随机选用车型时最低碳排放量相差不大.优先选用碳排放系数高的车辆时最低碳排放量比优先选择碳排放系数低的车辆或者随机选取车型时都要高，而碳排放系数高的车型载重量大，碳排放量低的车型所需要的车辆更多，发车成本会相应增加，而用随机选取车型时加适合，在成本和减排方面都可以做到比较满意.

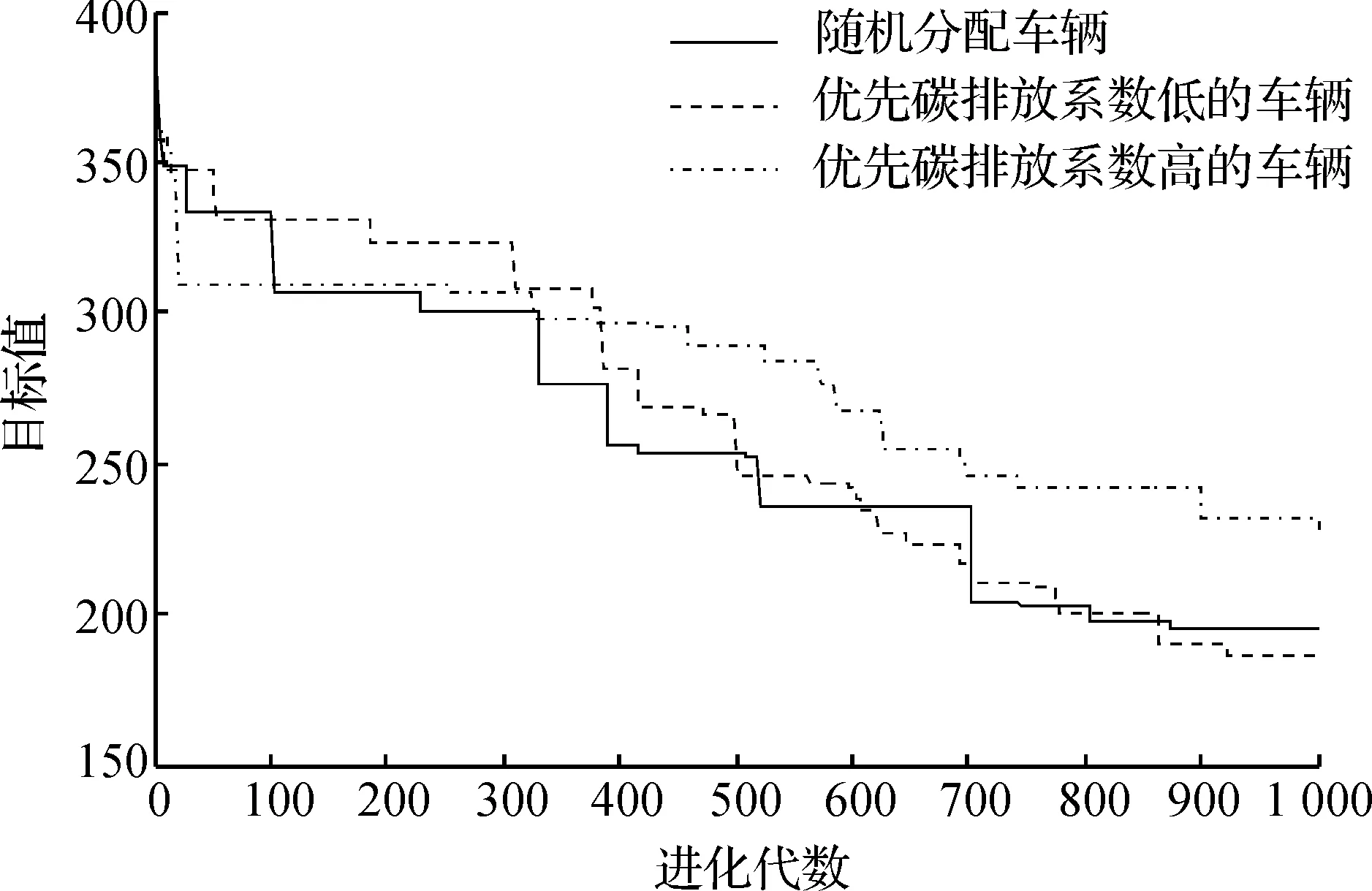
图3　车辆不同方式选用时目标函数收敛图Fig.3　The objective function convergence when vehicle is different chosen

上述采用的模型目标函数都是使碳排放量最小，为了对实验结果有一个全面的了解，我们对总碳排放量最小为目标函数与车辆配送总路径最小为目标函数下的试验结果进行对比，两种方式下都采用随机分配车辆模型，两种不同目标函数下的车辆总路径和碳排放量的实验结果如图4，5所示.

图4　总碳排放量最小时的总路径曲线和总碳排放量曲线Fig.4　The total routing curve and Carbon emissions curve for the minimum carbon emission

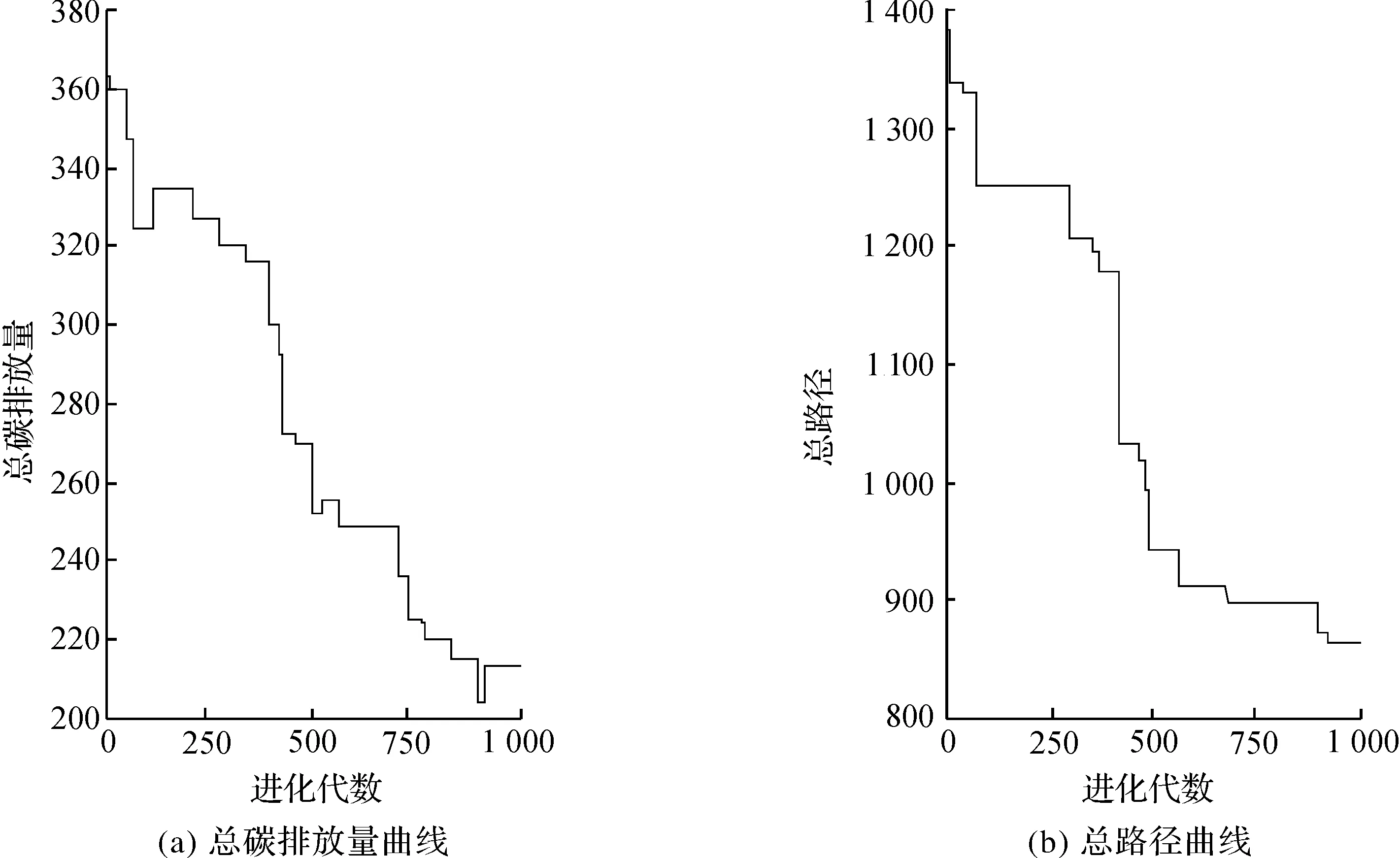
图5　总配送最小时的总路径曲线和总碳排放量曲线Fig.5　The total routing curve and Carbon emissions curve for the minimum routing

由图6，7比较可以看出：以总碳排放量最小为目标函数时的碳排放量为195 t左右，其对应的总路径为900 km，而以总路径为目标函数时的碳排放量为210 t左右，其对应的总路径为890 km左右，由数据对比，选择减少碳排放对总路径的增加影响不大，但是碳排放的减少却有很有效果，将近减10%的碳排放，所以以节能减排作为目标，对车辆配送调度有很重大的意义.

4结论

对于多车型同时取送货问题，首先对问题进行了描述，然后建立了该问题的模型.并通过量子进化算法对问题进行了求解，同时通过对车型的不同分配方式，比较了优先选用碳排放系数高的车型、碳排放系数低的车型和随机选取车型时碳排放总量的变化，最后比较了以总碳排放量最小为目标与总路径最小为目标时模型中碳排放和总路径的变化.实验表明，通过量子进化算法的求解，能够有效的求解多车型同时取送货问题，同时，随机选取车辆有助于减少车辆配送时的碳排放和发车成本，而且，以碳排放为目标时对总路径的增加影响不大，而对碳排放的减少有很好的效果.当然，研究还存在很多方面的不足，仅仅以碳排放量最低作为目标函数，而且也没有考虑客户的货物配送的时间窗要求，在实际的配送系统中，目标函数中需要考虑经济成本的因素[20]，因为物流企业的发展就是要满足客户要求的同时使配送的成本最低，同时，客户对于货物的取送时间也有一定的要求，但是，低碳作为研究的目标对于物流企业配送降低碳排放提供了一定的参考意义，也可为相关政府部分节能减排政策提供一些有价值的借鉴.

参考文献：

[1]张思亮.基于改进粒子群算法的车辆路径问题研究[D].江南大学:江南大学,2011.

[2]姚锦宝,夏禾,贺兴东,等.同时取送货车辆路径问题的改进的蚁群算法[J].物流技术,2010(Z1):154-156.

[3]贾方方,孔德成.同时取送货车辆路径问题的改进粒子群优化算法[J].物流技术,2012(19):137-139.

[4]刘晴.随机需求同时取送货车辆路径问题建模及优化研究[D].南京航空航天大学:南京航空航天大学,2013.

[5]马宇红,姚婷婷,张浩庆.基于分区的多配送中心多车型车辆调度问题与遗传算法设计[J].科技导报,2013(2):534-535.

[6]钟石泉,贺国光.多车场有时间窗的多车型车辆调度及其禁忌算法研究[J].运筹学学报,2005(4):38-41.

[7]李进,傅培华.具有固定车辆数的多车型低碳路径问题及算法[J].计算机集成制造系统,2013(6):245-248.

[8]史春阳,赵磊.同时取送货的车辆路径问题中的低碳研究[J].计算机集成制造系统,2011(5):122-126.

[9]关丽霞.带软时间窗和同时取送货的车辆路径问题研究[D].中南大学:中南大学,2012.

[10]叶志坚,叶怀珍,周道平,等.多车型车辆路径问题的算法[J].公路交通科技,2005(5):89-91.

[11]经怀明,张立军.多车型车辆调度问题的建模与仿真[J].计算机仿真,2006(4):445-447.

[12]KIRBY H R, HUTTON B, MCQUAID R W, et al. Modeling the effects of transport policy levers on fuel efficiency and national fuel consumption[J]. Transport and Environment,2000(6):265-282.

[13]杨培颖,唐加福,于洋,等.面向最小碳排放量的接送机场服务的车辆路径与调度[J].自动化学报,2013(4):367-369.

[14]王钰青,许茂增.基于最小碳排放的广义TSP模型研究[J].数学的实践与认识,2012(8):56-58.

[15]邱雅君,宋国防.考虑碳排放因素的车辆路径问题研究[J].物流技术,2012(13):222-226.

[16]赵燕伟,彭典军.有能力约束车辆路径问题的量子进化算法[J].计算机集成制造系统,2008(8):124-128.

[17]李川.基于混合量子进化算法的随机车辆路径问题的研究[D].杭州:浙江工业大学,2012.

[18]秦本涛.基于遗传算法的车辆调度系统设计[D].杭州:浙江工业大学,2011.

[19]吴斌.车辆路径问题的粒子群算法研究与应用[D].杭州:浙江工业大学,2008.

[20]陈晓眯.基于混合禁忌搜索算法的动态车辆路径研究[J].浙江工业大学学报，2009，37(5)：24-28.

(责任编辑：刘岩)

作者简介：赵燕伟(1962—)，女，河南郑州人，教授，主要从事数字化产品现代设计理论与方法、数字制造/数字装备建模与仿真的基础理论等，E-mail：zyw@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(61402409)；Foudation items：Project supported by the National Natural Science Foundation，China(61402409)

收稿日期：2014-09-18