失速颤振检测

张宇

（哈尔滨汽轮机厂有限责任公司，哈尔滨 150046）

0 引 言

在评估容积流量越来越高的现代涡轮的动态特点时，有必要考虑叶片在比设计点的流量相对减少的条件下的颤振响应。当涡轮在这种情况下工作时，低压末级叶片将会受到流量的影响，特别是在大的负攻角的情况下影响更大。

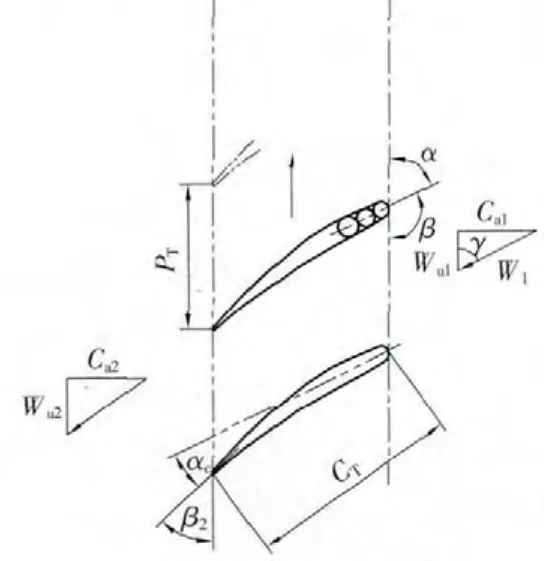
图1 叶片顶部几何尺寸

一般来说，气动升力、阻力与翼型的力矩特性将展示为大的负攻角失速现象，当负攻角超过某个临界值时，这种迹象就更明显。在失速颤振迹象中力或力矩的斜度相对于冲角是变化的。从动态的角度来看，失速颤振现象是可能的，在这种情况下，叶片组的振动将成为自激特定的模式，没有纯粹的理论知识来解释这个问题的存在性。

同时可以理解的是，因为缺乏知识，我们对于涡轮叶片的受迫振动问题很难评价。没有准确的信息或知识，我们必须诉诸经验因素。下面的设计方法仅基于对低压末级叶片可利用的知识和经验。

1 一阶模态颤振的设计指南

1）一阶模态颤振的设计指南如图2，其横坐标x计算公式为

其中：kf为应力集中系数，拉筋处为1.5，叶片拉筋附近为1.25，叶片底部为1.25，固定点的根部为2.4；σREL1为相对叶片应力的幅值乘以弹性模量（在一阶模态KfσREL1/σOSC1取最大值时）；σOSC1为材料所允许的疲劳极限应力（简化为在一阶模态KfσREL1/σOSC1取最大值时的离心应力）；CT为叶片顶部弦长；ZREL1为叶顶位移幅值，ZREL1=为叶顶轴向位移幅值（在一阶模态中查找），ΔY为叶顶切向位移幅值（在一阶模态中查找）；MR为质量流量比（最大绝对背压下的质量流量，随着背压的变化而变化为叶顶横截面面积，δ为对数衰减系数，钢制叶片的δ为0.002。

2）图2纵坐标y的计算公式为

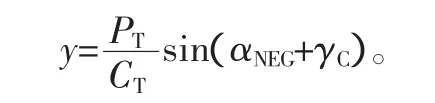
其中：PT为叶顶节矩；αNEG=180°-β，β是叶型进口几何角；γC=180°-（β+β2），β2是叶型出口几何角。

图2 一阶模态颤振曲线

3）用横坐标和纵坐标画点。

4） 参数 MTv1计算公式为

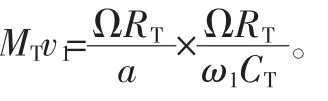
其中：Ω 为 2π/60与汽轮机转速的乘积；RT为叶片顶径；a为叶顶进口音速，a=W1/MT，W1为叶顶进口相对速度，MT为进口相对马赫数；ω1为预测一阶模态叶片的固有频率乘以2π。

5）根据计算出的MTv1值画出如图2平行线，如果画出的点在图2中的MTv1代表线的左侧，那所设计的叶片就不容易发生一阶模态颤振，如果画出的点在图2中的MTv1代表线的右侧，那么就应当重新审查所设计的叶片。

2 二阶和三阶模态颤振的设计指南

1）二阶和三阶模态颤振的设计指南如图3，其横坐标x计算公式为

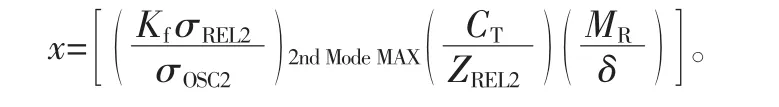
其中：Kf与一阶模态颤振列出的数据说明相同；σREL2为相对叶片应力的幅值乘以弹性模量（在二阶模态KfσREL2/σOSC2取最大值时）；σOSC2为材料所允许的疲劳极限应力（简化为在二阶模态KfσREL2/σOSC2取最大值时的离心应力）；CT、ZREL2、MR、δ的计算方法跟一阶模态颤振相同。

2）纵坐标跟一阶模态颤振的纵坐标相同。

3）根据计算出来的横坐标和纵坐标画点。

4）参数v2计算公式为

其中，Ω、RT、ω2、CT跟一阶模态的定义一样，只是数据来源于二模态颤振。

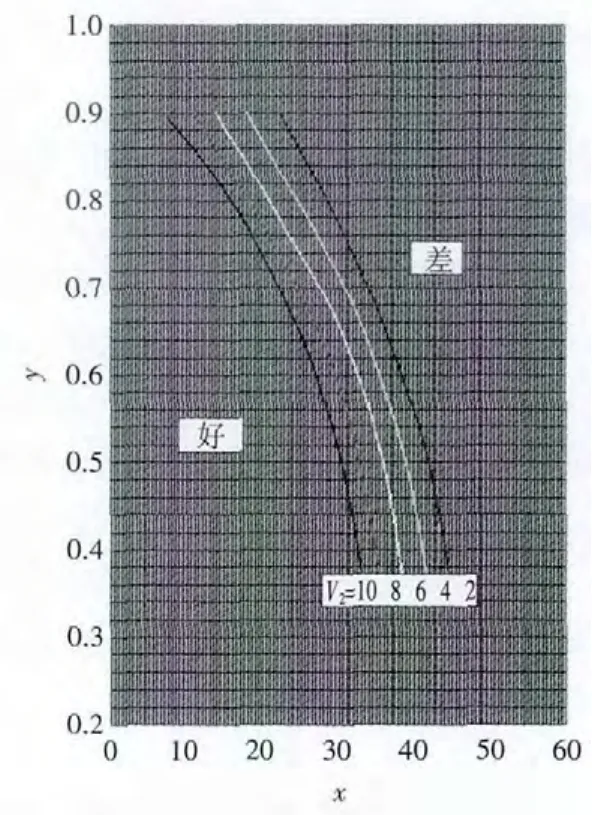
图3 二阶和三阶模态颤振曲线

5）根据计算出的v1值画出平行线（如图 3），如果先前根据横坐标与纵坐标计算出的值画出的点位于图3中的v2代表线的左侧，那所设计的叶片就不容易发生二阶模态颤振，如果画出的点在图3中v2代表线的右侧，那所设计的叶片就应当重新审查设计。

3 共振振动的设计指南

1）共振振动设计指南参照图4，图中的横坐标x计算公式为

式中：σREL1与一阶模态定义一样；σOSC1为材料的疲劳极限应力，简化为离心式稳态蒸汽弯曲应力，由一阶模态的放大倍数法确定；ZREL1与一阶模态定义一样；σREL2与二阶模态定义一样；σOSC2与二阶模态定义一样；ZREL2与二阶模态定义一样。

2）图4中的纵坐标y的计算式为

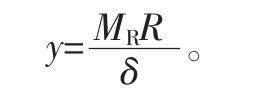
式中：MR为质量流量比，其中ρT为叶顶进口稳态密度，ρBLD为叶片材料的密度；R的计算公式为

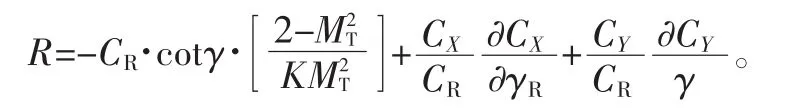
其中：γ在图1中有定义，通过速度三角形计算得出γ；MT为叶顶进口相对马赫数其中，Ca2为叶顶出口绝对轴向速度，PIN为叶顶进口静压，PEX为叶顶出口静压sinγ为叶顶出口相对切向速度；CR=

3）根据横坐标与纵坐标计算的值画出点。

图4 共振曲线

［1］ Pigott R.Interim design guides for avoidance of failure of last row L.P.baldes due to stall flutter and resonant vibrations［C］//Proceedings of the Institution of Mechanical Engineers,EM-312，April，1973.