佛像移位基础托换关键技术分析

杨上清　卢文胜　唐　俊

(同济大学土木工程学院, 上海 200092)



佛像移位基础托换关键技术分析

杨上清卢文胜*唐俊

(同济大学土木工程学院, 上海 200092)

摘要某寺庙大雄宝殿需移位保护,考虑将内部佛像一并移走。目前佛像托换没有相关的理论支撑和技术规范而成为本工程的难点。分析了佛像做法及结构性能,提出了佛像基础托换的方法,以及影响托换的主要因素,包括总体控制参数,土体侧移和托换土体尺寸等。通过建立ANSYS有限元模型进行数值分析,对侧向位移以及土体尺寸的影响进行了探讨,最后得到有指导意义的结论。

关键词佛像, 基础, 托换技术, 控制参数, 数值分析

Key Technology of Foundation Underpinning for Buddha Statue Moving

YANG ShangqingLU Wensheng*TANG Jun

(College of Civil Engineering,Tongji University, Shanghai 200092, China)

AbstractThe great Buddha's hall and its Buddha statue in a temple is supposed to be moved for preservation and protection. Buddha statue underpinning is a key technology for this project since there are no theoretical guidance and technical specifications for this aspect. After analyzing components of the Buddha statue, a method of Buddha statue underpinning was proposed, which consider several influencing factors, such as overall parameter, lateral soil movement, and the volume of soil. A finite element model was established to analyze these factors and some useful results were provided.

Keywordsbuddha statue, foundation, underpinning technology, control parameter, numerical analysis

1引言

建筑物移位是指通过一定的技术手段,在保持建筑物整体性的条件下,改变建筑物的空间位置,包括平移、旋转、抬升、迫降等单项移位或组合移位[1]。建筑物移位最早出现在国外,国内的技术也已发展成熟,成功的工程案例越来越多[2-3]。

现有的托换移位技术主要针对具有一定结构性能的建(构)筑物[4],由于这类建(构)筑物具有诸如梁、柱等传力构件,因此可以根据其传力途径对主要的受力构件进行托换,并与托换主梁进行连接,形成有效托换层,以保证后续移位就位的安全传力。

但是,对传统佛像而言,既没有可靠的结构体系及持力构件,也没有清晰可靠的传力途径,很难按现有技术规范进行托换,而且出于保护的要求,不能破坏其外形装饰。现有的研究鲜有涉及佛像托换移位,更没有相关的托换方法用于指导施工。针对此问题,本文以某古建筑佛像移位工程为背景,根据已有托换经验,提出佛像托换的方法,并对其关键技术进行了分析,以期为相关工程提供借鉴。

2工程介绍

2.1　概况

某寺庙主体结构于1918—1928年建成,其大雄宝殿内供奉有三尊大佛(图1)和二十四诸天。其中三尊大佛的尺寸为2 m×2 m×6 m,二十四诸天的尺寸为11 m×5 m×1.8 m。佛像需要同寺庙一起进行移位保护。

图1　三尊单体大佛Fig.1　Three giant Buddha

2.2　佛像“结构”

佛像“结构”一般分为内部骨架和外部泥塑两部分。内部骨架一般由木骨架、砖瓦、草茎等组成,其主要做法是在形成主心木的基础上,以钉木条或扎稻草的方式形成顺应外形的骨架(图2)。外部泥塑根据其黏性和可塑性,由内至外分别采用粗泥和细泥[5]。佛像所用木材、草茎、泥土的材料参数如表1所示,从表中可以看出各种材料的密度及强度相差较大,难以给出一个明确的值用于佛像的承载力计算,且各种材料的连接状态也不明晰,更增加了评估佛像承载力的难度。同理,在本工程中,佛像无可靠传力体系,且承载能力不确定,不能对其直接进行托换,转而考虑对其下部的座台或者基础进行托换。

图2　佛像骨架常见做法简图Fig.2　Common construction practices of theBuddha statue skeleton

2.3　佛像座台

佛像座台可分为特殊座台和一般的座台。特殊的座台主要用于带有坐骑的佛像,一般的座台即为普通的莲花座。座台从下往上依次可以分为三个部分[6]:①从地面而起的基座,又称神座,一般由砖石建造; ②基座以上为金刚座,又称须弥座,其内胎可用砖石土木建造,外部辅以神兽、祥云等雕刻;③金刚座以上为莲花座。上部佛像一般通过骨架插入的方式与下部座台连接(图3)。座台一般由石块等材料堆砌而成,且无有效连接,难以作为托换对象承受托换移位时的各种荷载,因此,本文认为对其下部基础进行托换是必然之选,值得进行研究。

图3　佛像托换简图Fig.3　Buddha statue underpinning diagram

表1组成佛像材料参数

Table 1　Parameters for the Buddhastatue composition

现有的移位工程虽有地基土体的托换,如大型古木[7]以及沉船[8]的移位托换,但缺少明确的托换方法及相关规范。因此,本文提出一种针对佛像基础托换的施工方法,以期为相关工程提供参考。

3佛像托换方法

3.1　佛像托换方法

综上所述,佛像无可直接承力体系,下部座台整体性能很差,本文拟对座台下部基础进行整体加固托换(图3),其主要步骤如图4所示。

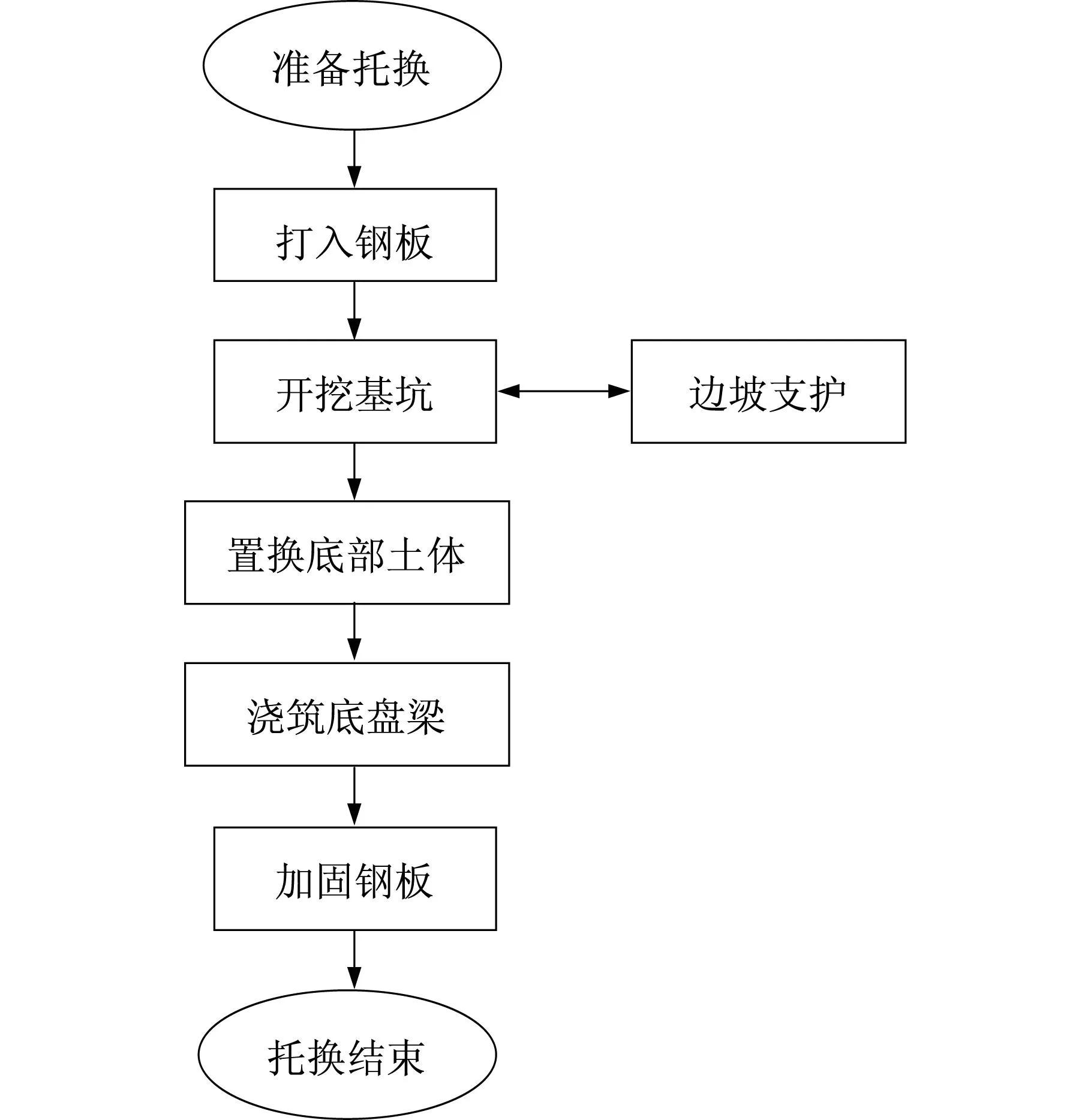
图4　佛像托换步骤Fig.4　Underpinning steps of buddha statue

3.2　受力模式

在托换的过程中,佛像及托换土体会受到各种荷载的作用(图5),而这些作用直接影响了佛像及土体的安全性,如何考虑这些作用的影响并提出抵抗的措施,是托换能否顺利进行的关键。

图5　地基与佛像简图Fig.5　Buddha statue and foundation

4佛像托换影响因素探讨

4.1　总体控制参数

如式(1)所示,在托换移位的过程中,佛像会受到轴力N、剪力V与弯矩M等荷载作用,其骨架及地基必须具有足够的承载能力才能保证其在托换移位过程中的安全。

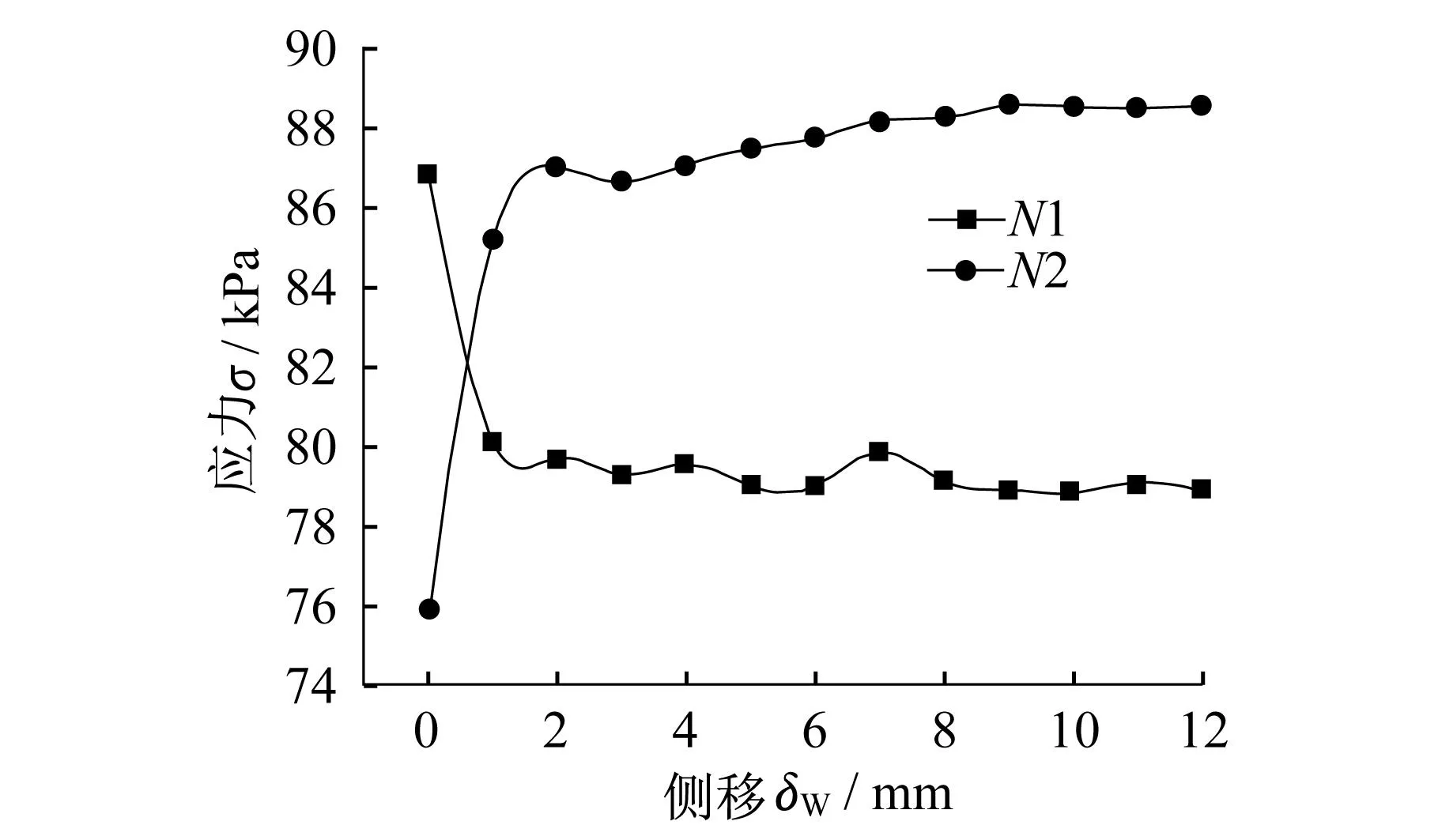
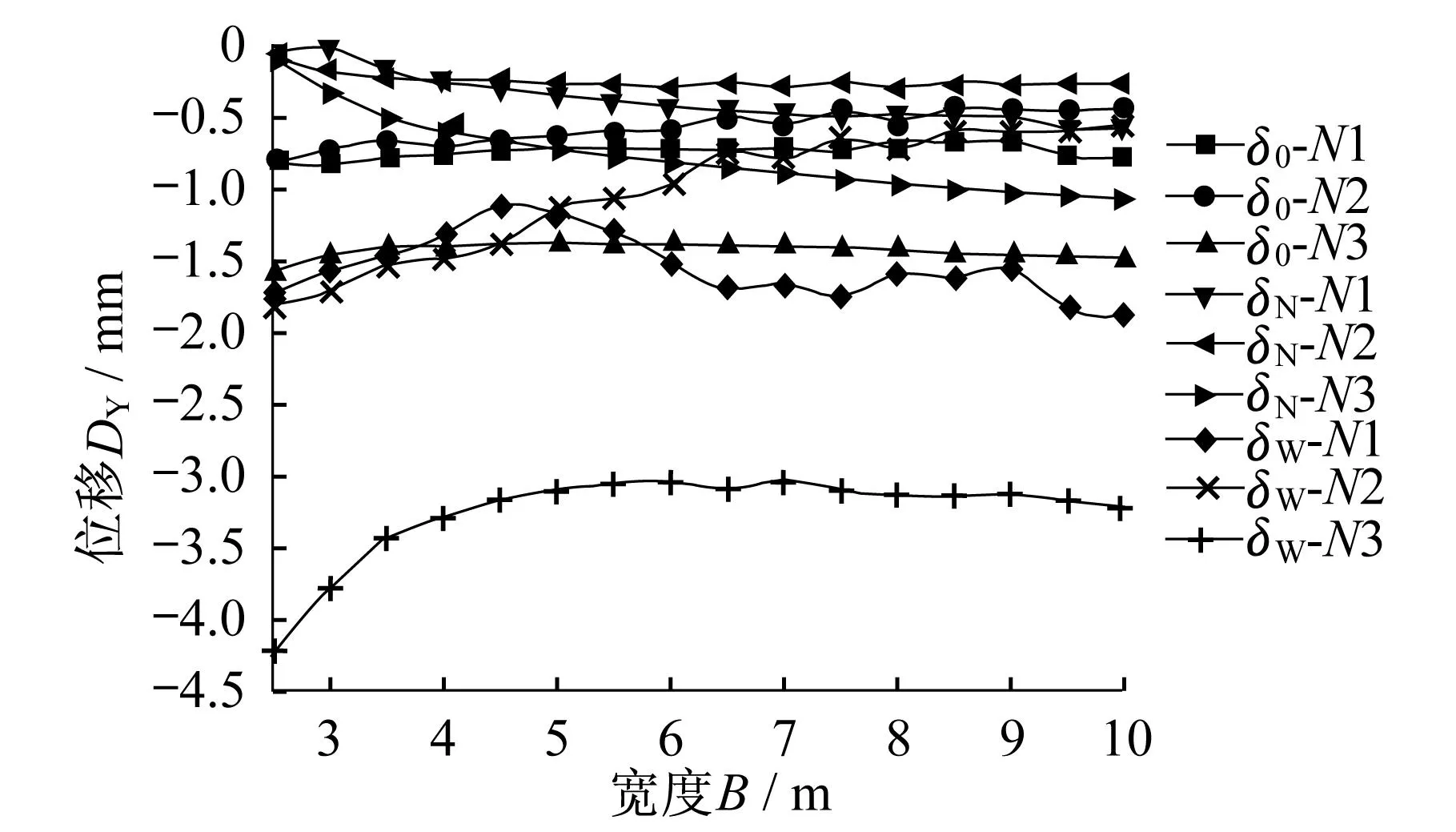
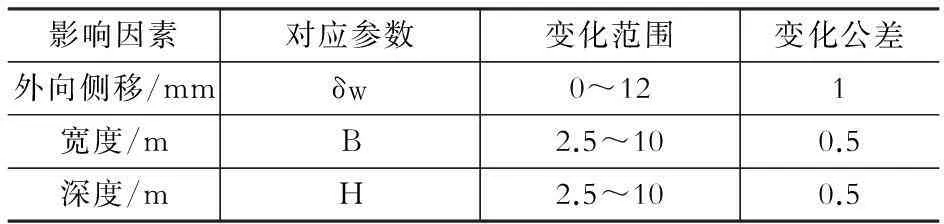
S(N,V,M)

(1)

式中,S为佛像承受的作用;N为佛像承受的轴力;V为佛像承受的剪力;M为佛像承受的弯矩;R为佛像地基的承载能力;σ为托换时内的等效应力;τf为土的抗剪强度;δ为托换时土体承受的内、外向侧移;B为托换土体宽度;H为托换土体深度。

在托换移位的过程中,地基土会受到冲击荷载、往复荷载等动态作用,也会受到诸如附加压力、钢板侧向位移等静态作用。动态作用主要是施工引起,可通过改善施工工艺和方法来加以控制;而静态作用主要由佛像及土体侧向钢板造成,需要对其进行具体分析,找出规律,从而指导施工。

4.2　建模与关键参数选取

为深入探讨各个因素对地基土的影响,以图1中一个单体大佛地基为研究对象,建立有限元模型。由于下部托换土体一般为矩形,其两个方向受力基本一致,因此将此土体受力情况简化为平面问题,以PLANE42单元建立ANSYS有限元模型(图6)。

图6　有限元模型Fig.6　Finite element model

将上部座台的压力等效为100 kN/m的均布压力施加在模型顶部,约束底部竖向位移,通过对模型侧面施加水平位移来模拟内向侧移δN与外向侧移δW对土体的影响。模型在计算过程中始终受到重力作用。选取模型中的部分节点作为特征点,其中N1位于N3正下方2 m处,N2位于N1与模型左部边缘的中点处。其主要建模参数如表2所示,各个影响因素及其取值见表3。

表2有限元模型主要参数与取值

Table 2Main parameters of finite element model

表3影响因素及取值

Table 3　Influence factor values

4.3　托换影响因素分析

4.3.1外向侧移的影响

采用图6所示模型,通过对模型侧边施加外向位移来模拟托换土体受到的外向侧移δW。提取节点等效应力σ、X方向位移反应DX和Y方向位移反应DY进行分析,计算结果如图7-图8所示。

图7　侧移增加时节点应力变化规律Fig.7　Nodal stress variation with theincreasing of lateral displacement

从图中可以看出,σ在最开始阶段随着δW的增加而迅速变化,当δW达到2 mm时,应力趋于稳定。而随着δW的增加,节点位移不断增加,基本呈现线性关系。

图8　侧移增加时节点位移变化规律Fig.8　Nodal displacements with theincreasing lateral displacements

综上所述,托换钢箱内的土体对外向侧移δW十分敏感,很小的δW即会让土体内部产生较大的应力和位移变化,因此,在对土体进行托换时,应充分考虑这一特征,控制土体不出现外向侧移δW,保证其在整个托换移位过程中的稳定。

4.3.2托换土体宽度B的影响

仍采用图6的有限元模型,保持深度H为4 m不变,宽度B从2.5 m到10 m持续变化,分为无侧移、δW=1 mm和δN=1 mm三种情况,其典型节点的等效应力σ、Y向位移DY变化规律如图9、图10所示。图中,δ0表示无侧移,δN表示向内侧移1 mm,δW表示向外侧移1 mm。

由图9可以看出,随着B的增加,节点应力不断减小。而向内侧移1 mm,能显著增加各节点的应力。

图9　宽度增加时节点等效应力变化规律Fig.9　Nodal stress variation with the increasing width

由图10可以看出,随着B增加,各节点DY均呈增加的趋势,且当土体受到δN作用时,各节点DY均显著小于同一B处δ0和δW的值。

对于土体而言,较大的σ可使固体颗粒之间连接更紧密,有利于整个土体的稳定。为了保证佛像不出现倾斜,土体内部各点Y向位移DY越小越好。随着宽度B增加,各节点σ逐渐减小,DY逐渐增加。因此在满足施工要求和上部结构嵌固要求的前提下,土体宽度B越小越好。在存在δN的情况下,土体σ较大,DY很小,因此,适当的内向侧移有利于托换土体的稳定。

图10　宽度增加时节点Y向位移变化规律Fig.10　Nodal displacement variation in the Ydirection with the increasing of width

4.3.3托换土体深度H的影响

当B保持为4 m不变,H持续增加时,其典型节点的σ、DY变化规律如图11-图12所示。

图11　深度增加时节点等效应力变化规律Fig.11　Nodal stress variation with increasing depth

图12　深度增加时节点Y向位移变化规律Fig.12　Nodal displacement variation in Ydirection with the increasing depth

由图11可以看出,随着H的增加,各节点σ均呈现波动性,但变化幅度不大,可认为H变化对节点应力影响不大。由图12可以看出,随着H增加,各节点DY逐渐增加。相较于无侧移的情况,向外侧移1 mm,节点应力σ会小幅度减小,节点DY会大幅增加;向内侧移1 mm,节点应力σ会大幅度增加,而DY会大幅减小。

在分析托换深度对土体的影响中,DY起控制作用,且H越小DY越小,当H为2.5 m时,各节点DY已经可以忽略不计。而适当的δN能够有效提高土体内部应力σ和减小y向位移DY。因此在确定土体H时,可将H控制在1.5~3 m的范围内,辅以一定大小的δN,能够有效保证土体的稳定。

5结论

本文以某寺庙佛像移位工程为背景,提出佛像基础托换的具体方法,并对影响单体佛像托换的因素作了具体分析,得到如下结论:

(1) 佛像托换会受到动态作用和静态作用,动态作用可以通过改善施工工艺来加以避免,静态作用则难以避免,因此需要特别关注静态作用产生的影响。

(2) 当内向侧移δN=1 mm时能有效提高托换土体内部的等效应力σ,同时减小各点的Y向位移反应DY,从而提高土体的稳定性;而当外向侧移δW=1 mm时会产生相反的效果。因此,在托换时,可适当顶推钢板,使土体产生一定的δN,以提高其稳定性。

(3) 在满足上部结构嵌固要求的前提下,托换土体的B和H越小越好,其中B大于上部佛像座台平面尺寸即可,H一般取1.5 m~3 m为宜。

参考文献

[1]中国工程建设标准化协会标准.CECS225:2007建筑物移位纠倾增层改造技术规范[S].北京:中国计划出版社,2008.

China Association for Engineering Construction Standardization.CECS225:2007.Technical code for moving,incline-rectifying,story-increasing and reconstruction of buildings[S].Beijing:China Planning Press,2008.(in Chinese)

[2]Pryke J F S.Relevelling,raising and re-sitting historic buildings[C].Proc.Symp.IABSE,London,1983.

[3]Kim Brownie.From boca raton to fort pierce[J].The Structural Mover,1999,17(1).

[4]梁峰,卢文胜.移位技术与建筑结构安全问题[J].结构工程师,2004(5):24-27.

Liang Fen,Lu Wensheng.Translocation technology and structural security[J].Structural Engineers,2004(5):24-27.(in Chinese)

[5]王彬羽.民间造像匠工贾玉龙造型思维研究[D].西安:西安美术学院,2011.

Wang Binyu.Modeling thought of Jia Yulong in folk Buddhist art[D].Xi’an:Xi’an Academy of Fine Arts,2011.(in Chinese)

[6]王锡.佛教造像法[M].天津:天津人民出版社,2011.

Wang Xi.The art of creating Buddhist images[M].Tianjin:Tianjin People’s Publishing House,2011.(in Chinese)

[7]张任杰.我国古树名木全冠整体移位技术领先国际[J].城市道桥与防洪,2008(6):177-178.

Zhang Renjie.The technology of Ancient trees movingin China is in a leading position[J].Urban Road and Bridge and Flood Control,2008(6):177-178.(in Chinese)

[8]吴建成,孙树民.“南海1号”古沉船整体打捞方案[J].广东造船,2004(3),69-72.

Wu Jiancheng,Sun Shumin.The salvage plan of “The south China sea No.1”[J].Guangdong Ship Building,2004(3),69-72.(in Chinese)

收稿日期：2015-07-04

*联系作者， Email:wally@tongji.edu.cn