钢梁-混凝土墙全螺栓连接节点受力性能分析

余　琼　方永青　朱　帅

(同济大学结构工程与防灾研究所, 上海 200092)



钢梁-混凝土墙全螺栓连接节点受力性能分析

余琼方永青*朱帅

(同济大学结构工程与防灾研究所, 上海 200092)

摘要采用ABAQUS对钢梁-混凝土墙全螺栓半刚性连接节点进行分析研究,结果表明,钢梁-混凝土墙全螺栓连接节点滞回曲线饱满,具有较好的耗能能力;节点的初始刚度和抗弯承载力随着角钢厚度、钢梁高度、抗滑移系数的增大而增大,随轴向力、螺栓孔中心到角钢长肢边的距离增大而减小。采用正交回归分析得到节点初始刚度与抗弯承载力公式。

关键词全螺栓, 半刚性连接, 梁墙节点, 正交分析

MechanicalBehaviors of a Fully-Bolted Connection Joint Between Steel Beam and Concrete Wall

YU QiongFANG Yongqing*ZHU Shuai

(Research Institute of Structural Engineering and Disaster Reduction,Tongji University, Shanghai 200092, China)

AbstractA fully-bolted semi-rigid connection joints between a steel beam and a RC wall were analyzed with ABAQUS. Results show that the fully-bolted semi-rigid connection joints between a steel beam and a RC wall hasa good energy dissipation capacity. The initial stiffness and bending capacity of the joint increase with the decrease of the axial load and the distance of bolt hole center to the angle steel′s long lamp. It can also be enhanced by increasing the thickness of the angle steel, the height of the steel beam, and the anti-slipping coefficient.The orthogonal experiment and regressions analysis were adopted to achieve approximate formula for the initial stiffness and the bending capacity of the joint.

Keywordsfully-bolted, semi-rigid connection, beam-wall joint, orthogonal analysis

1引言

钢-混凝土组合结构是在钢结构和钢筋混凝土结构基础上发展起来的一种新型结构形式,在高层和超高层建筑中具有明显的优势,尤其是框架-核心筒混合结构,被认为是一种符合我国国情的超高层建筑结构形式[1]。钢框架与混凝土核心筒的连接节点是结构受力最复杂的区域,地震的震害表明,节点部位是结构破坏的多发部位,节点的破坏往往导致整个结构的倒塌,因此对于节点研究具有现实意义。闵宗军等[2]提出的梁与剪力墙之间的全螺栓半刚性连接在不改变核心筒混凝土墙体滑模施工工艺的情况下实现了全螺栓连接,便于施工过程中调整施工误差,操作简单。目前对于钢结构梁柱节点半刚性连接的研究已有较系统的理论,但对于钢梁与混凝土连接的半刚性节点的研究较少,本文采用ABAQUS分析闵宗军等[2]的试验,调整参数,分析钢梁与混凝土墙半刚性连接节点的力学性能。

2有限元模型的建立

有限元模型以文献[2]中的节点试件S-1,S-2,S-3为原型,采用与试验试件相同的尺寸进行实体建模(BASE-1,BASE-2,BASE-3)。该节点的立面示意图如图1所示。试件细部构造见表1。

图1　试验节点模型示意图(单位:mm)Fig.1　Details of the tested connection joints (Unit:mm)

为节省计算机资源,根据对称性建立半边模型。螺栓头和螺母按公称尺寸将六边形近似换算成圆形考虑,不对螺纹精确建模,螺栓头和螺栓帽以及螺栓杆均采用圆柱体模拟,建模时考虑螺孔与螺栓杆之间的空隙,螺栓孔比螺栓杆直径大2 mm。螺栓头和螺栓帽的垫片不单独考虑。模型中考虑角钢与锚板、角钢与钢梁、螺栓头与角钢、螺栓杆与螺栓孔壁之间的接触。此外,还考虑了穿筋预埋件的锚筋与混凝土墙体之间的粘结滑移作用,粘结滑移本构关系采用混凝土规范给出的钢筋-混凝土粘结滑移本构关系。带弯钩锚筋作为构造措施[2],故模型中忽略了带弯钩锚筋的作用。

混凝土材料本构模型采用ABAQUS提供的损伤塑性模型,强度等级与试验保持一致。混凝土受压受拉应力应变曲线选取混凝土强度等级C35时的受压受拉应力应变全曲线[3]方程。钢筋、角钢、钢梁、锚板以及高强螺栓应力应变关系均采用三折线模型,对应屈服强度及抗拉强度见表2。高强螺栓采用10.9级。

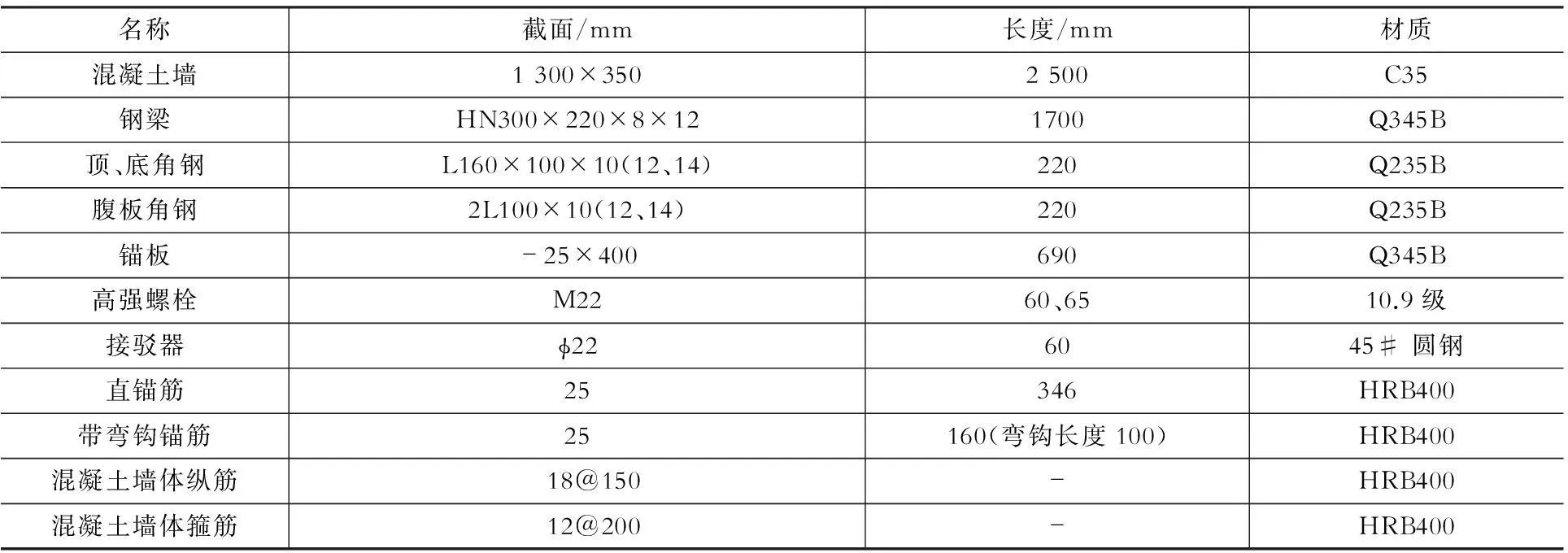
表1　试件细部构造Table 1　Details of the model

表2　钢材材性试验数据Table 2　Experimental data of steel material parameters

模型中,实体单元采用C3D8R单元,钢筋采用T3D2单元。在节点附近进行网格细化。与试验时的边界条件一致,混凝土墙体顶部与底部施加完全约束,梁端施加位移荷载前对螺栓施加预紧力,10.9级M22高强螺栓预紧力为190 kN。后续分析步中将螺杆的长度设置保持不变,持续加载全部过程。边界约束及作用力示意如图2所示,加载制度按照位移控制。

3有限元计算与试验结果对比

节点的初始转动刚度是指连接在梁端弯矩作用下,其变形仍处于线弹性范围内时连接所具有的刚度。在弹性阶段可以用节点初始刚度来反映节点的半刚性。本文参考文献[2,4-5],约定节点的弹性极限状态为节点中的组件(梁、墙、角钢、螺栓)应力首次达到屈服应力前的状态。由于M-θ曲线在初始弹性阶段几乎是理想线弹性节点,节点的初始转动刚度为弹性阶段的定义为割线刚度。

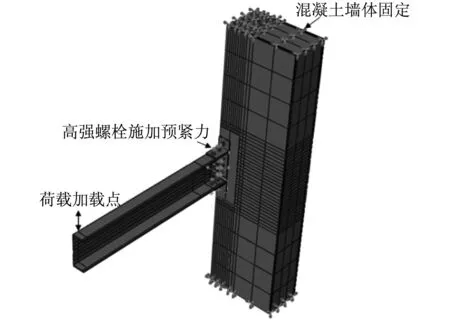
图2　节点边界约束及作用力示意图Fig.2　Boundary conditions of the joint

采用上述建模方法,对文献[2]中的试件S-1,S-2,S-3进行非线性有限元模型分析,得到节点的荷载-位移滞回曲线与骨架曲线,其中,S-2有限元模拟结果与试验实测结果对比情况如图3、图4所示。从图中可以看出,有限元模拟的曲线和试验得出的滞回曲线、骨架曲线吻合程度较好。

图3　梁端荷载-位移滞回曲线对比Fig.3　Comparison of force-displacement hysteresiscurves at the beam-end

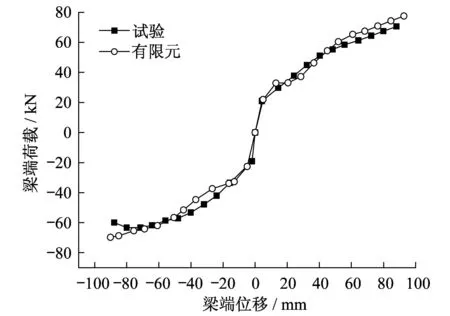
图4　梁端荷载-位移骨架曲线对比Fig.4　Comparison of force-displacementskeleton curves at the beam-end

三个节点模型的初始刚度误差在11.3%以内,节点弯矩承载力误差在16.1%以内,节点极限转角误差在5%以内。可知本文所建立的有限元模型选用的混凝土与钢材材料本构关系、单元划分、边界条件等是合理有效的,能够有效地模拟文献[2]试验节点在低周反复荷载作用下的抗震性能。

4节点参数对受力性能的影响分析

以下参数分析均基于BASE-2进行建模。由于从试件的M-θ曲线中看不出结构有明显的破坏阶段,参考文献[6]中定义塑性极限破坏状态为

(1) 当连接转角达到0.045 rad前,出现以下某种情况时认为结构破坏:顶底角钢或腹板角钢应变超过断裂应变;高强螺栓产生滑移;梁翼缘或腹板屈服;螺栓孔塑性应变过大;锚筋断裂;锚板出现明显变形;墙体混凝土出现明显破坏等。

(2) 未出现以上情况未时,连接转角达到0.045 rad。

节点转角定义为:θ=(u1-u2)/(h-tf),其中,u1,u2分别为梁受拉翼缘和受压翼缘中心处的侧移,h为钢梁高度,tf为钢梁的翼缘厚度。

4.1　角钢与钢梁接触面抗滑移系数的影响

改变角钢与钢梁接触面的抗滑移系数(0.1,0.25,0.35,0.5),分析抗滑移系数对节点初始刚度和抗弯承载力的影响,结果见图5。

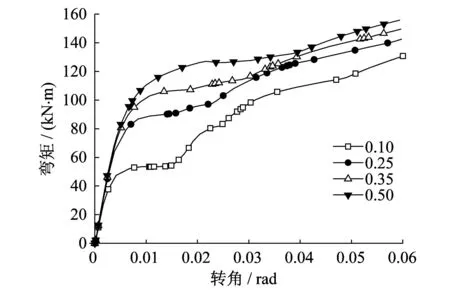
图5　不同抗滑移系数的节点M-θ曲线Fig.5　M-θ curves for the joints withdifferent slipping coefficients

由图5可知,随抗滑移系数的增大,节点的初始刚度、屈服荷载和抗弯承载力逐渐增大,但增加的幅度逐渐减小。在抗滑移系数较小时,节点有明显的屈服平台,随抗滑移系数的增加,屈服平台逐步消失。产生以上现象的原因是:随抗滑移系数的增大,节点破坏机制逐渐发生变换,在抗滑移系数较小时,节点在破坏之前首先在螺栓连接处发生滑移,导致屈服平台的产生,并且随抗滑移系数的增大,螺栓连接处不再产生滑移,结构的初始刚度和抗弯承载力增大。

4.2　钢梁高度的影响

改变梁的高度,建立不同梁高(250 mm,300 mm,350 mm,400 mm)的有限元模型,分析节点的受力性能。摩擦面抗滑移系数取0.35。

图6为不同钢梁高度的节点M-θ曲线。由图6可知,梁高对节点抗弯刚度及抗弯承载力影响较为显著,随着梁截面高度的增大,抗弯承载力和初始刚度都增大。但从有限元模型中看到,相应梁高越大,锚板周围混凝土的破坏就越大。

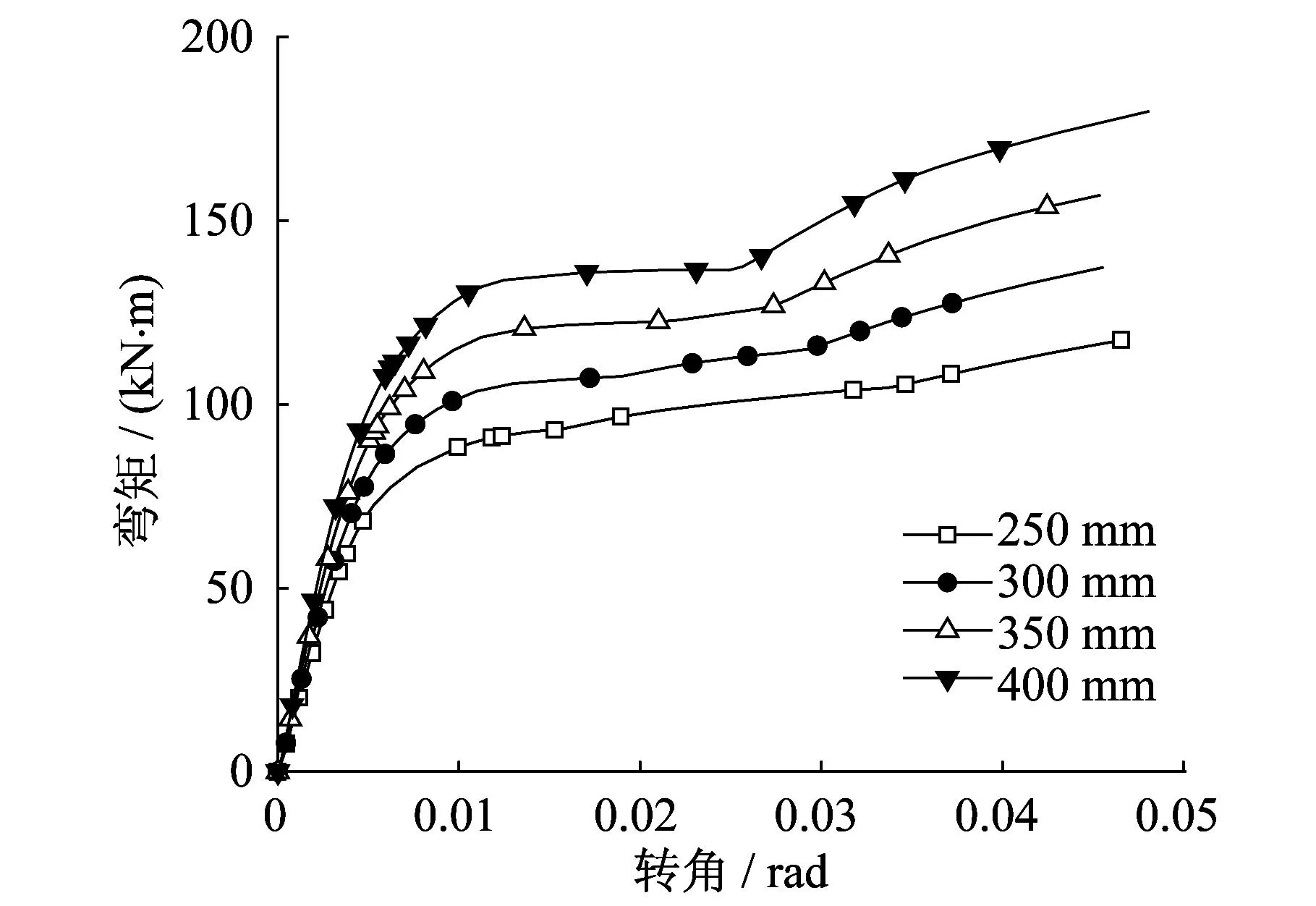
图6　不同钢梁高度的节点M-θ曲线Fig.6　M-θ curve for the joints with different beam height

4.3　顶底角钢与腹板角钢厚度的影响

改变顶底角钢与腹板角钢厚度(8 mm,10 mm,12 mm,14 mm,16 mm)建模分析该因素对节点抗弯刚度和抗弯承载力的影响。

图7为不同角钢厚度的节点M-θ曲线。由图7可知,顶底角钢与腹板角钢厚度是影响节点受力性能的重要因素。节点的初始抗弯刚度、屈服荷载及抗弯承载力随顶底角钢和腹板角钢厚度的增加而增大,且随顶底角钢和腹板角钢厚度的增加导致屈服平台的产生。

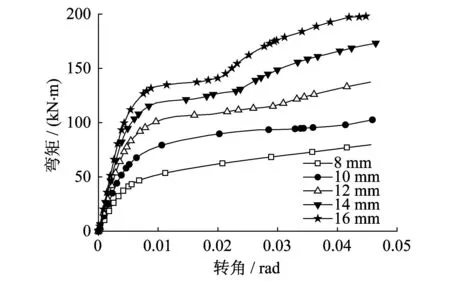
图7　不同角钢厚度的节点M-θ曲线Fig.7　M-θ curve for the joints with different thicknessof angle steel

4.4　螺栓直径的影响

改变螺栓直径(16 mm,20 mm,22 mm,24 mm)建立有限元模型,其中摩擦面抗滑移系数取0.35。图8为不同螺栓直径的节点M-θ曲线。由图8可知螺栓直径对节点的受力性能有一定影响。随螺栓直径的越大,节点的初始转动刚度、抗弯承载力有一定程度的增加。

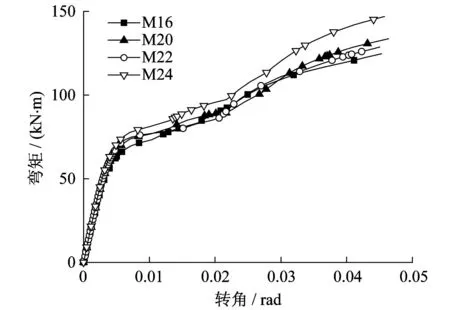
图8　不同螺栓直径的节点M-θ曲线Fig.8　M-θ curves for the joints with differentthickness of angle steel

4.5　加劲肋的影响

在顶底角钢中部设置加劲肋,改变加劲肋厚度(0 mm,4 mm,6 mm,8 mm,10 mm,12 mm,14 mm,16 mm)建立有限元模型考察加劲肋厚度对比顶底角钢加劲肋的影响。根据文献[6]设计本文加劲肋,尺寸如图9所示。

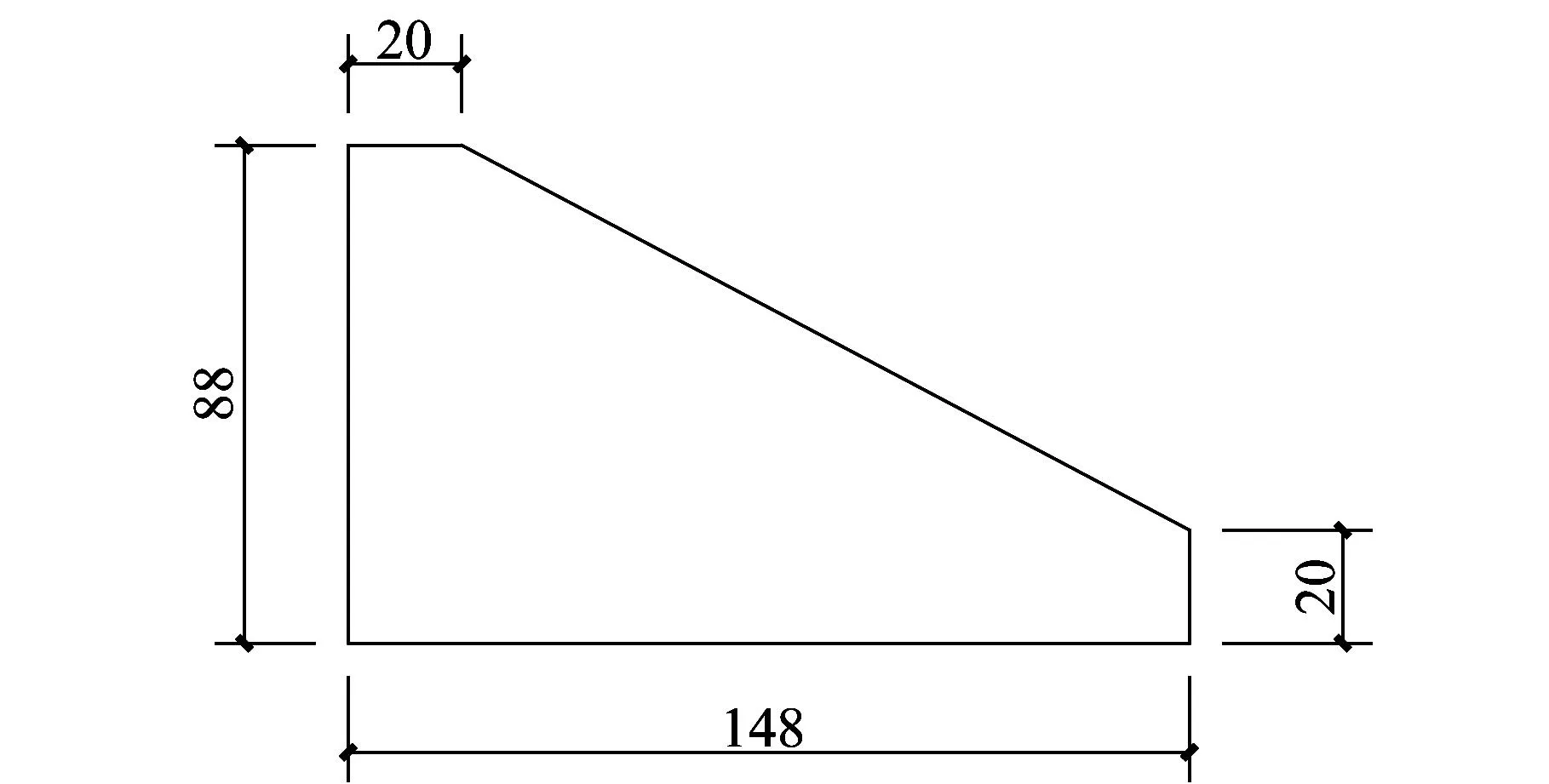
图9　顶底角钢加劲肋几何尺寸(单位:mm)Fig.9　Stiffener details for the angle steelat the top and the bottom (Unit:mm)

图10为不同加劲肋厚度的节点M-θ曲线。从图10可知,有无加劲肋对节点的初始转动刚度及承载力有较为显著的影响,产生这一现象的原因是因为顶底角钢在设置了加劲肋之后,角钢抗弯刚度及抗弯承载力增大。但加劲肋厚度的增加对节点的初始刚度和极限承载力的影响程度逐渐降低,在一定厚度范围内,节点初始刚度及承载能力随着加劲肋厚度的增大而增大幅度逐渐下降。因此,可以根据实际情况适当选用加劲肋厚度,在满足构造要求的基础上可以选取厚度较薄的加劲肋。

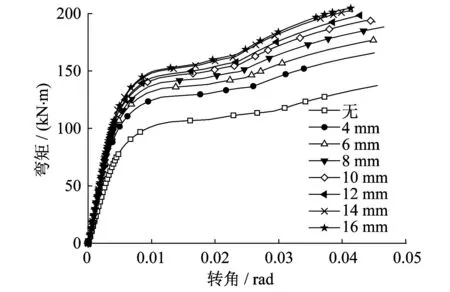
图10　不同加劲肋厚度的节点M-θ曲线Fig.10　M-θ curve of the joints with differentthickness of stiffener

4.6　沿钢梁轴向拉力的影响

文献[7]建立不同轴力(0 kN,100 kN,200 kN,300 kN,400 kN)影响下节点的有限元计算模型,ABAQUS计算结果见图11。

图11　不同轴向拉力大小的节点M-θ曲线Fig.11　M-θ curves for the joints with different axial forces

分析发现轴向拉力对节点的初始转动刚度有显著影响。随着轴向拉力的增加,节点的初始转动刚度不断减小,屈服平台消失。这是由于在轴力的影响下,顶底角钢的变形较大,进而节点的初始刚度变小、变形增大。此外,节点的轴向拉力还会降低节点的抗弯承载力。因此,建议对全螺栓半刚性连接的钢梁-混凝土墙节点的承载力计算时尚应考虑地震引起的轴力。

4.7　角钢与锚板相连的螺栓孔中心到角钢长肢边的距离g的影响

改变角钢与锚板相连的螺栓孔中心到角钢长肢边的距离g(55 mm,63 mm,70 mm,78 mm,85 mm),如图12所示。建立有限元模型,研究该因素对节点性能的影响。

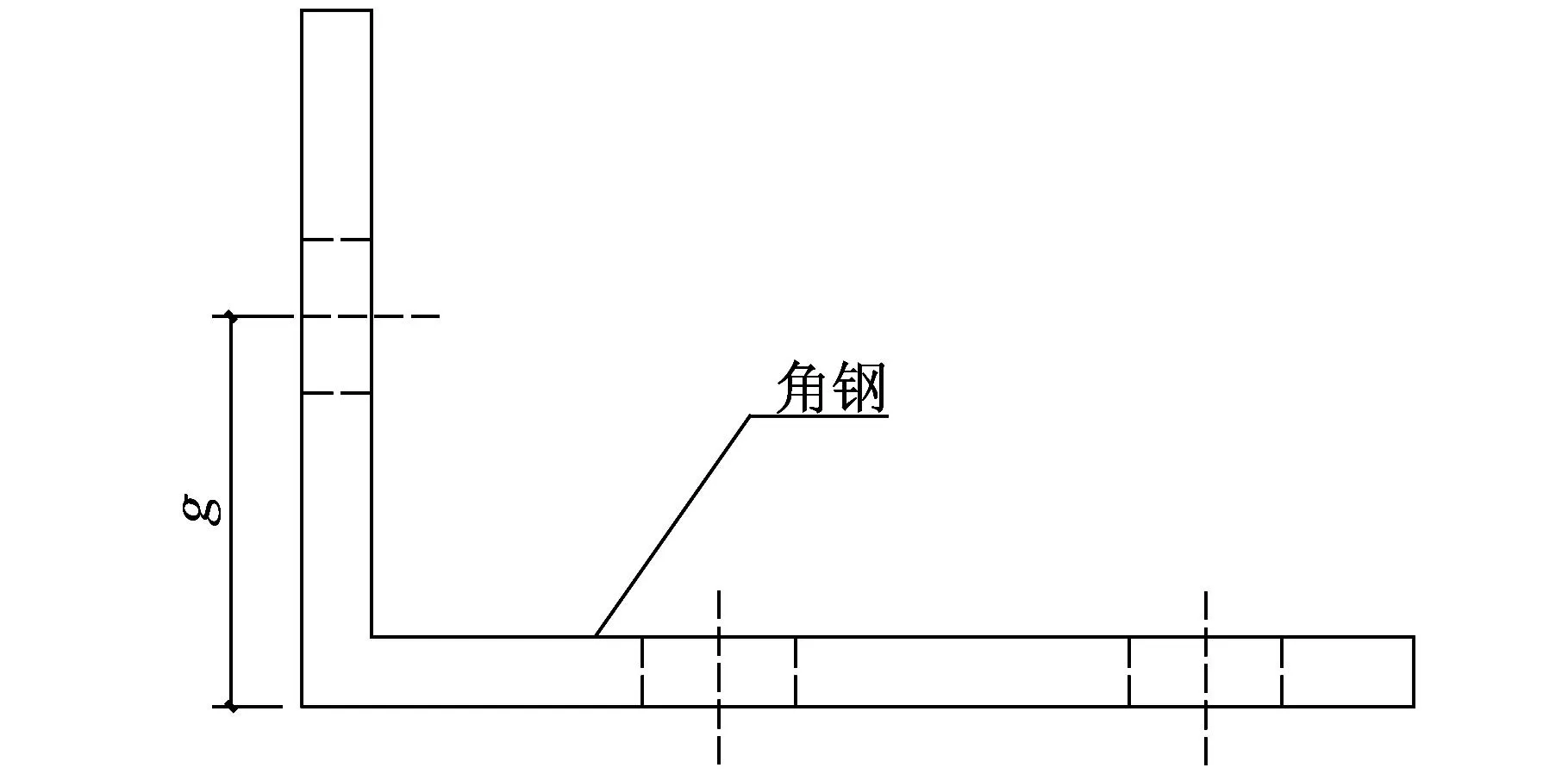
图12　距离g示意图Fig.12　Sketch of the distance g

ABAQUS分析计算得到的节点的弯矩-转角曲线如图13所示。g值变化对节点的初始转动刚度影响较大,g值越大,节点的初始转动刚度越小。这是由于距离g的增加降低顶底角钢两肢上螺栓孔之间的抗弯刚度,进而导致节点抗弯刚度的降低。随着g值的增大节点抗弯承载力也减小,这也是顶底角钢两肢上螺栓孔之间的变形过大导致的。

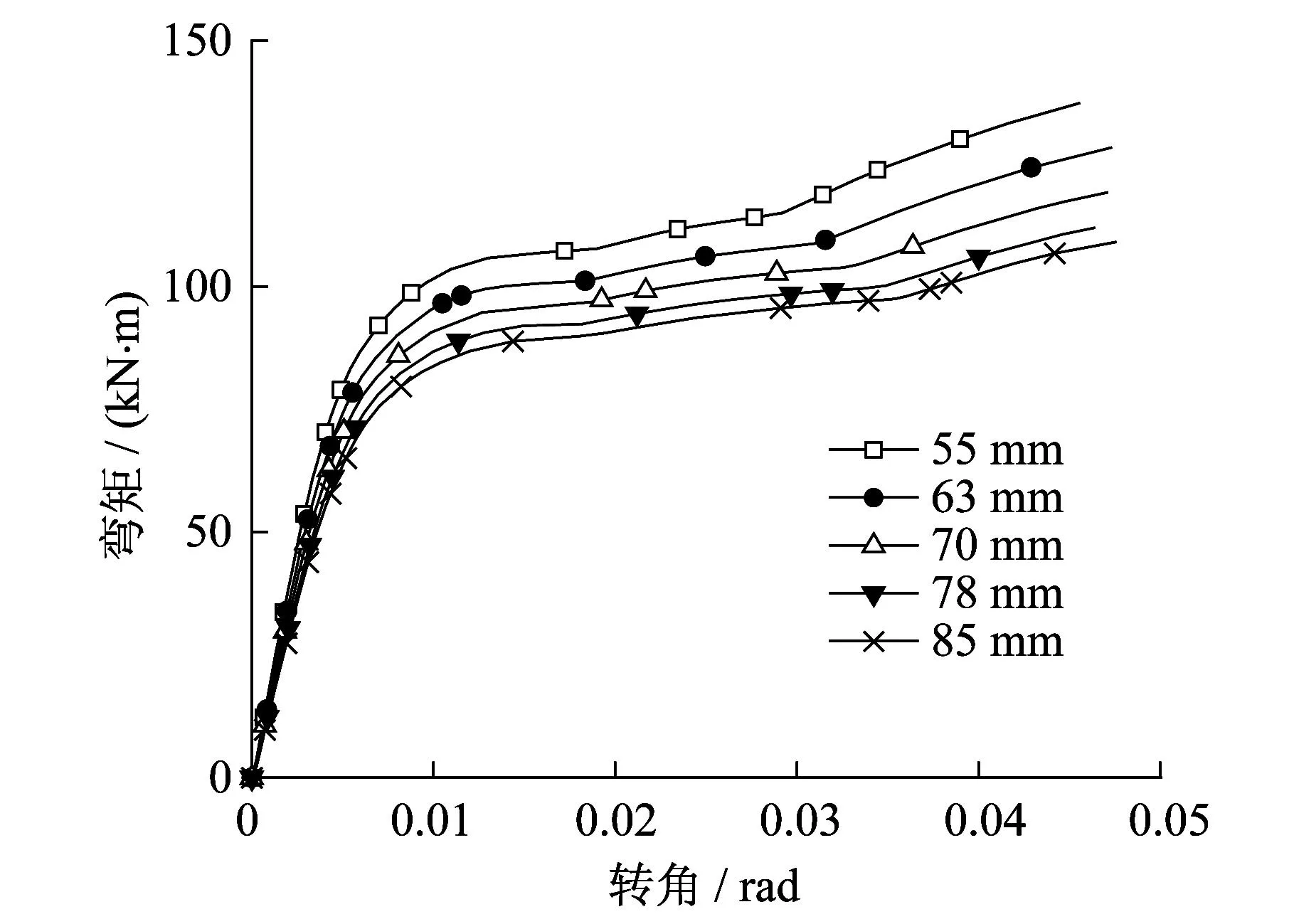
图13　不同距离g的节点M-θ曲线Fig.13　M-θ curve of the joints with different distance g

4.8　节点耗能能力

在反复荷载作用下,耗能系数是评价结构抗震耗能能力的一个重要指标。以上文建立的有限元模型为基础,按照《建筑抗震试验规程》规定的加载制度,对节点进行滞回分析,节点滞回曲线较为饱满,梁墙全螺栓连接节点耗能系数在1.44~2.09之间,说明该类型节点具有较强的耗能能力。模型信息及各模型耗能系数见表3。

5正交模拟以及回归分析

5.1　正交模拟

选择5种对节点性能影响较显著的因素,每个因素选择3个有代表性的水平,按L18(37)正交表的试验设计方法进行组合(表4),建立18个有限元模型,分析各因素对节点受力性能的影响程度的大小。这5种因素分别为顶底角钢与腹板角钢厚度、角钢与锚板相连的螺栓孔中心到角钢长肢边的距离g、梁截面高度、摩擦面抗滑移系数和高强螺栓规格。

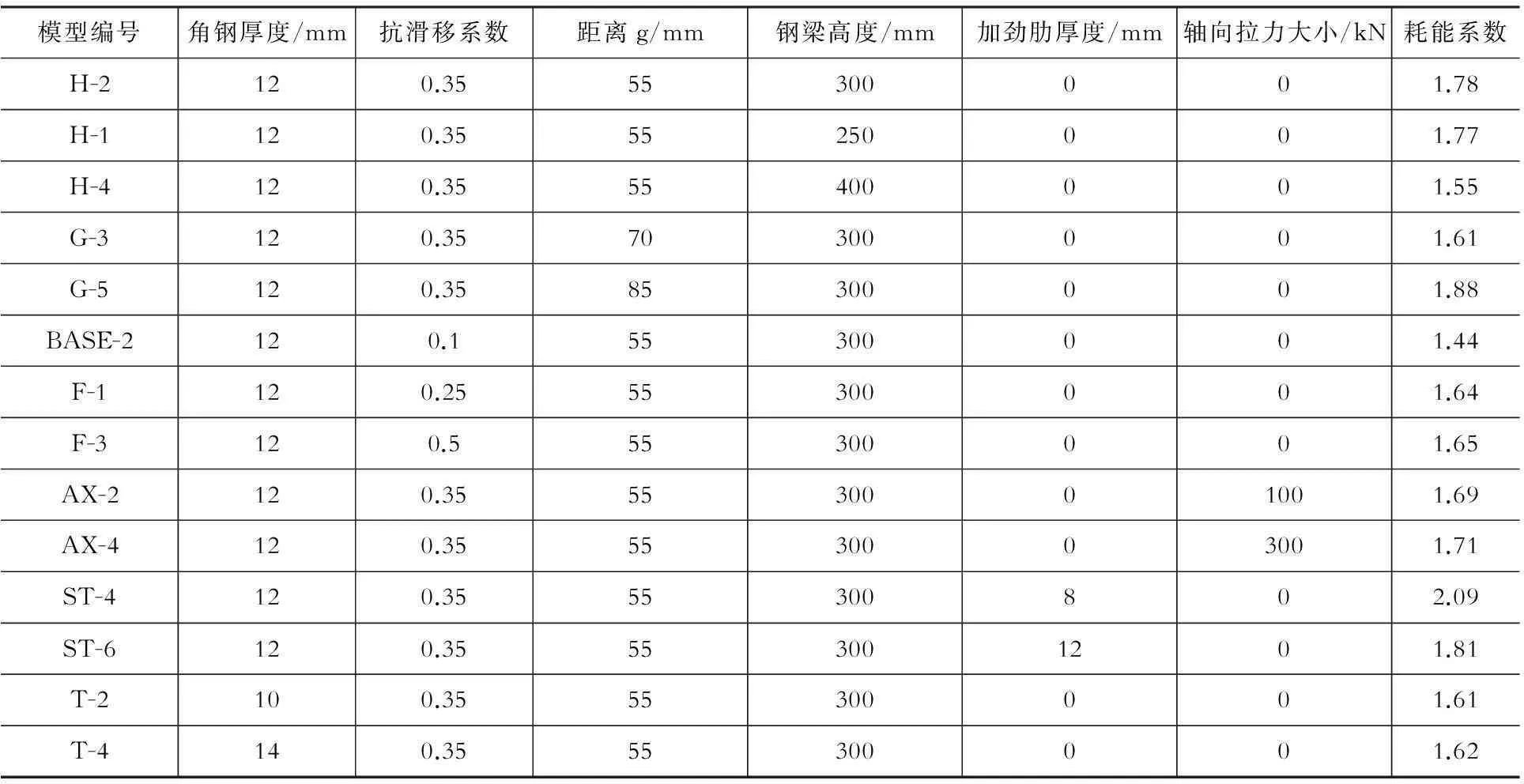
表3　模型信息及对应耗能系数Table 3　Model information and relative energy dissipation coefficients

表4　正交模拟因素、水平表Table 4　Factors and levels in the orthogonal experiment

将角钢厚度记为t,角钢与锚板相连的螺栓孔中心到角钢长肢边的距离记为g,钢梁高度记为h,抗滑移系数记为μ,高强螺栓直径记为d。参考文献[5,8]所得到的M-θ关系曲线方程,对梁墙全螺栓连接节点进行分析,选取常用的幂函数表达式：

R=Ctα1gα2hα3μα4dα5

(1)

式中,C为一常数;α1,α2,α3,α4,α5分别为与各影响因素相关的系数。

5.2　节点初始转动刚度回归分析

采用式(1),代入具体数据拟合得到节点初始转动刚度的回归方程:

R=0.00851t1.357g-1.165h0.692μ0.473d1.235

(2)

回归结果的拟合优度为0.91583,这表明该模型对数据的拟合程度比较高。通过观察t值可知,各因素对初始刚度的影响主次顺序为顶底角钢与腹板角钢厚度、角钢与锚板相连的螺栓孔中心到角钢长肢边的距离、高强螺栓直径、钢梁截面高度、摩擦面抗滑移系数。

5.3　节点抗弯承载力回归分析

采用式(1),代入具体数据拟合得到节点抗弯承载力回归方程

M=0.0669t1.358g-0.594h0.943μ0.2577d0.497

(3)

回归结果的拟合度为0.98128,这表明该模型对数据的拟合程度比较高。通过观察t值可知,各因素对初始刚度的影响主次顺序为顶底角钢与腹板角钢厚度、钢梁截面高度、角钢与锚板相连的螺栓孔中心到角钢长肢边的距离、高强螺栓直径、摩擦面抗滑移系数。

5.4　试验结果与回归分析结果对比

将试验结果与回归计算结果进行对比,结果见表5。

表5　试验结果与回归分析结果对比Table 5　Comparison between testing results and regression results

由表5可以看出,对于节点初始转动刚度,试验结果与回归分析结果误差较大,最大达-28.33%。对于极限弯矩承载力(本节中试验的极限承载力取值与有限元模型中定义的破坏状态一致,均取为节点转角为0.045 rad时的节点承载力值),试验结果大于回归分析结果,考虑一定的安全系数,对式(3)进行0.85的折减(表5),结果表明误差有所降低,且偏于安全,建议设计中节点抗弯承载力计算采用0.85的折减系数。

6结论

通过以上分析，可得到以下结论:

(1) 钢梁-混凝土墙全螺栓连接节点具有典型的半刚性连接性质,滞回曲线饱满,有着较好的耗能能力。

(2) 节点的初始刚度和抗弯承载力随着角钢厚度、钢梁高度、抗滑移系数的增大而增大,随螺栓孔中心到角钢长肢边的距离的增大而减小。顶底角钢设置加劲肋可以显著提高节点的受力性能。

(3) 钢梁轴向拉力的存在对节点的受力性能有显著影响,轴向拉力越大,节点初始刚度和抗弯承载力越低。

(4) 采用正交模拟得出各因素对初始刚度及抗弯承载力影响的程度及节点初始刚度及抗弯承载力回归方程。

参考文献

[1]聂建国,陶慕轩,黄远,等.钢-混凝土组合结构体系研究新进展[J].建筑结构学报,2010,31(6):71-80.

Nie Jianguo,Tao Muxuan,Huang Yuan,et al.Research advances of steel-concrete composite structural systems[J].Journal of Building Structures,2010,31(6):71-80.(in Chinese)

[2]闵宗军.混合结构T型墙梁半刚接耗能节点构造及受力性能研究[D].北京:北京建筑大学,2013.

Min Zongjun.Experimental study on construction and energy dissaption of T-shape wall-beam semi-rigid joint for steel-concrete hybrid structure[D].Beijing:Beijing University of Civil Engineering and Architecture,2013.(in Chinese)

[3]过镇海.钢筋混凝土原理[M].北京:清华大学出版社,1999:19-22.

Guo Zhenghai.Reinforced concrete mechanism[M].Beijing:Tinghua University Press,1999:19-22.(in Chinese)

[4]完海鹰.钢结构半刚性连接体系理论分析及实验研究[D].合肥:中国科学技术大学,2009.

Wan Haiying.Theoretical analysis and experimental on semi-rigid connections of steel structure[D].Hefei:University of Science and Technology of China,2009.(in Chinese)

[5]张景辉.梁柱双腹板顶底角钢连接受力性能的有限元分析[D].北京:北京交通大学,2013.

Zhang Jinghui.Finite element analysis of mechanical behavior of top-seat and web angles beam-column connections[D].Beijing:Beijing Jiaotong University,2013.(in Chinese)

[6]郑廷银,徐士云,张玉.带加劲肋的顶底角钢与腹板双角钢连接的梁柱节点的试验[J].工业建筑,2008,38(4):87-90.

Zheng Tingyin,Xu Shiyun,Zhang Yu.Test on beam-collumn connection by top and seat angles with stiffer and double web angles[J].Industrial Construction,2008,38(4):87-90.(in Chinese)

[7]李国强,周向明,丁翔.高层建筑钢-混凝土混合结构模型模拟地震振动台试验研究[J].建筑结构学报,2001,22(2):2-7.

Li Guoqiang,Zhou Xiangming,Ding Xiang.Shaking table study on a model of steel-concrete hybrid structure tall building[J].Jounal of Building Structures,2001,22(2):2-7.(in Chinese)

[8]Tarpy T S,Cardinal J W.Behavior of semi-rigid beam-to-column end plate connections[J].Joints in Structural Steelwork,1981:2-3.

收稿日期：2015-05-20

*联系作者， Email:fyq8979@163.com