地下室及其周边回填土对上部结构的影响研究

邸　芃　安学旭

(西安科技大学建筑与土木工程学院, 西安 710054)



地下室及其周边回填土对上部结构的影响研究

邸芃安学旭*

(西安科技大学建筑与土木工程学院, 西安 710054)

摘要对于抗震嵌固端在地下室顶板处的高层建筑,建模计算分析时,地下室周边不同回填土对结构有何影响和结构模型计算是否需要带地下室,这是结构设计的一个重要环节。结合带地下室的结构力学模型和顶部水平位移理论计算公式,根据不同回填土与地下结构的相互约束特点,利用软件计算相同荷载作用下的五种不同约束框剪模型,对比分析了结构的自振周期、顶部水平位移和不同层墙、柱底内力变化曲线。结果表明,抗震嵌固端在地下室顶板处的高层结构,建模计算分析时宜带地下室,地下室周边回填土对上部结构刚度和承载力影响较小。

关键词抗震嵌固端, 回填土, 上部结构, 内力变化曲线

Study on the Influence of Basement and Surrounding Backfill on the Upper Structure

DI PengAN Xuexu*

(College of Architecture and Civil Engineering, Xi’an University of Science and Technology, Xi’an 710054, China)

AbstractUsually the fixed end at the top of the basement is assumed to establish models to calculate and analyze the characteristics of the high-rise building under seismic loading. It is an important process to consider the influence of backfill around the basement if the basement is considered in the structural model. Shear frame model with five different constraints were analyzed under the same load to study the interaction between different kinds of backfill and underground structure. Natural vibration periods, top horizontal displacement, and the internal force curves of the walls and the column at different floors were compared. The results show that it is more appropriate to take the basement into account when analyzing the model of a high-rise building under seismic loads. Different kinds of backfill around the basement have less impact on stiffness and bearing capacity of a structure.

Keywordsfixed end, backfill, the upper structure, internal force

1引言

21世纪以来,随着我国经济快速发展和城镇化的高速推进,城市土地资源变得日益稀缺。因此,形式各异的高层及超层建筑不断地涌现,使得带有地下超市、商场、停车场及人防工程等复杂的高层建筑得到了越来越多的应用[1-5]。可对于高层结构建模计算分析时,地下室周边不同回填土对上部结构有何影响和建筑结构计算模型选取是否需要带地下室等问题,目前,在不同的地区,不同工程做法尚不统一。

对于嵌固端在地下室顶层顶板处的高层结构,计算建模分析时不带地下室会带来一定误差,可能造成建筑材料浪费或者导致计算结果偏于安全。本着与实际情况相符的原则,带地下室进行计算建模更加合理,同时还应该考虑地下室周边回填土对结构的影响。沈朝勇[6]通过对相似比为1/25的大量带地下室结构模型进行了震动台试验,发现地下室外墙回填土与地下室之间的相互作用对结构侧移的减小有一定作用,采用有限元软件里的非线性弹簧模拟地下室外墙回填土对结构水平约束作用,得到的分析结果与试验结果比较吻合。

2力学模型及理论公式

2.1　力学模型

高层结构由基础、地下室、地上结构三部分组成,这三者之间受荷后相互约束和相互作用,按各自刚度对变形产生相互约束作用,从而使整个结构的杆件内力和变形发生变化。因此,将三者作为一个整体进行建模更加合理。

图1为高层结构实际模型和简化模型,该结构模型的地下室外墙回填土与地下室之间的水平约束用水平弹簧来模拟。弹簧刚度假定为k,k值的大小可以用来反映回填土对地下室的约束强度。

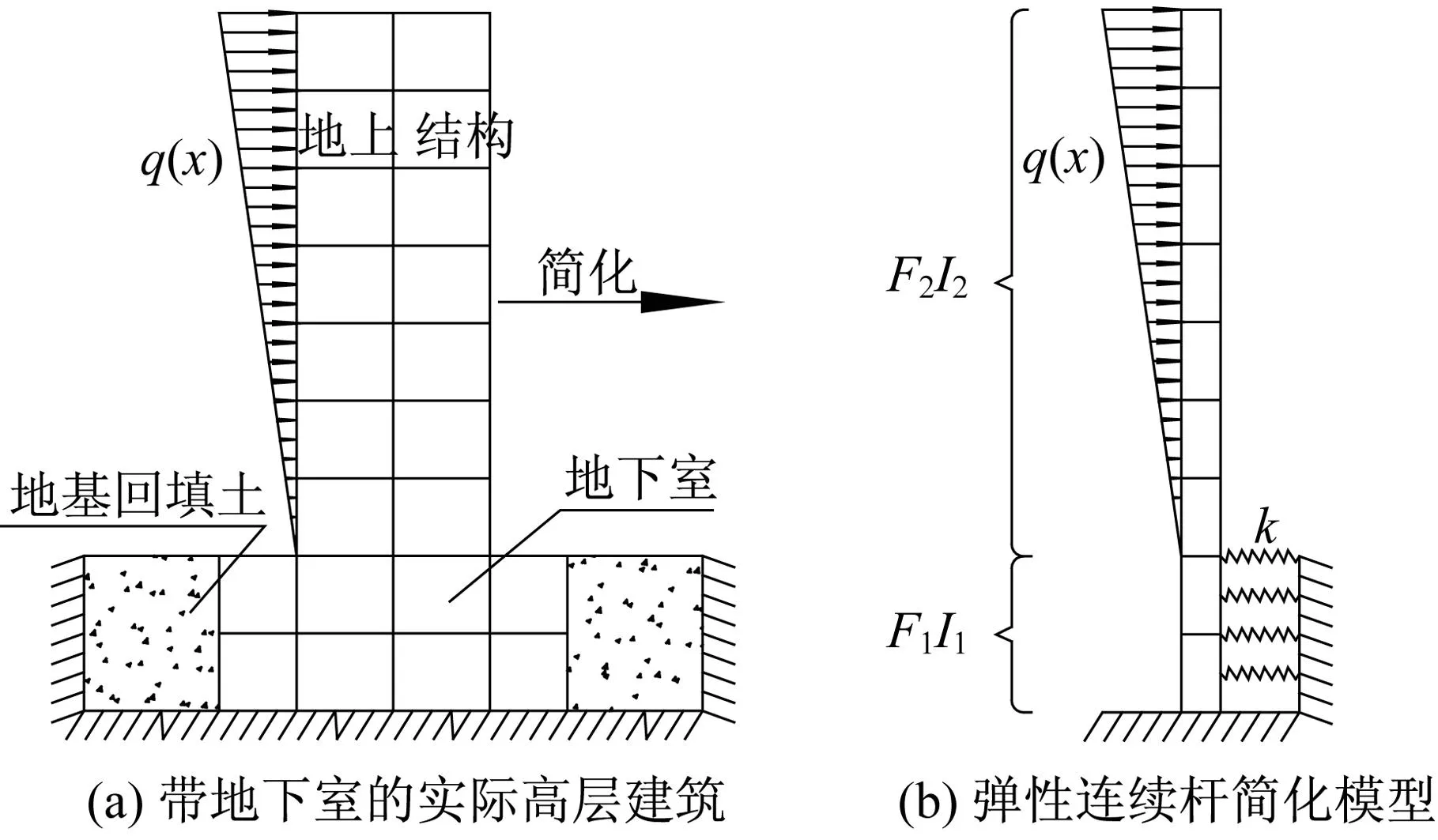
图1　含地下室的结构模型Fig.1　Structural model with the basement

2.2　基本假定

本文力学模型做了以下四条假定[7]:

(1) 整个结构的嵌固端位于地下室顶板处。

(2) 上部结构抗弯刚度为E2I2,下部结构抗弯刚度为E1I1,地基回填土水平反力系数为k。

(3) 不考虑建筑结构的剪切变形。

(4) 上部结构水平荷载为倒三角形分布。

2.3　理论公式

图2为结构侧移示意图。由叠加原理可知上部结构顶点水平位移为:

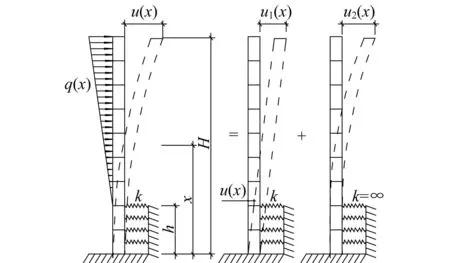
图2　结构侧移示意图Fig.2　Lateral displacement

U(x)=u1(x)+u2(x)(h≤x≤H)

(1)

u1(x)=u(h)+(x-h)u`(h)(h≤x≤H)

(2)

式中,U(x)为结构顶部水平总位移；u(h)为地下室顶板处水平位移； u1(x)为地下室顶板发生的水平位移u(h)和转角u′(h)引起上部结构顶部的位移之和;u2(x)为计算嵌固端在地下室顶板处,上部结构顶部的水平位移；h为地下室周边回填土厚度；H 为地下室与上部结构两者高度之和。

2.3.1侧向荷载和嵌固端内力

在水平荷载q(x)作用下,结构高度x处的侧向荷载值为：

(3)

由式(3)可求得地下室顶板处的弯矩和剪力值分别为:

(4)

(5)

2.3.2地下室

图3为地下结构荷载分布示意图。从地下室(x≤h)中取微元体d(x)。由剪力∑Q=0平衡方程和弯矩∑M=0平衡方程可知[8]:

(6)

式中,p (x)为地下室周边回填土的弹性约束反力；u(x)为地下室高度x 处的水平位移值。

由式(6)可得:

(7)

由材料力学挠度公式可知:

(8)

图3　地下结构荷载分布示意图Fig.3　Load distribution of the underground structure

由式(7)、式(8)可得:

(9)

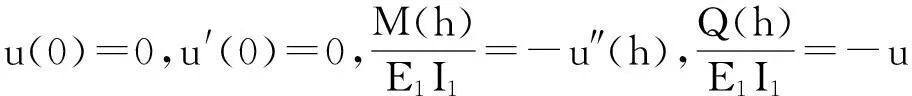
u(x)=C1[(eηx-e-ηx)cos(ηx)-

2e-ηxsin(ηx)]+C2(eηx-e-ηx)·

sin(ηx)(0≤x≤h)

(10)

式中,C1,C2为常量,具体取值如下:

(11)

(12)

ψ=[eηh+(2μ+3)e-hη]cos(ηh)+

(1-μ)(eηh+e-hη)sin(ηh)

(13)

φ=[γ(eηh+e-hη)+eηh-e-hη]cos(ηh)-

(eηh+e-hη)sin(ηh)

(14)

(15)

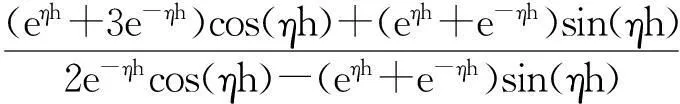
(16)

(17)

由式(10)可知地下室顶板处(x=h)的水平位移和转角分别为

u(h)=C1[(eηh-e-ηh)cos(ηh)-

2e-ηhsin(ηh)]+

C2(eηh-e-ηh)sin(ηh)

(18)

u′(h)=C1η[(eηh+e-ηh)cos(ηh)-(eηh-

e-ηh)sin(ηh)]+2C1ηe-ηh(sin(ηh)-

cos(ηh))+C2η[(eηh+e-ηh)sin

(ηh)-(eηh-e-ηh)cos(ηh)]

(19)

2.3.3地上结构

图4为地上结构荷载分布示意图。当高层建筑的地下室顶板作为上部结构计算嵌固端时,取微元体d(x),由剪力和弯矩平衡方程可得[9]:

(20)

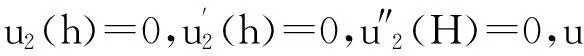
(h≤x≤H)

(21)

式中,B1,B2,B3,B4为常量,具体取值如下:

(22)

(23)

(24)

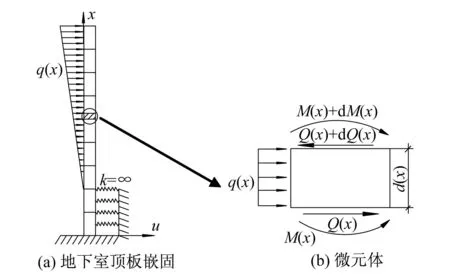
图4　地上结构荷载分布示意图Fig.4　Load distribution at the upper structure

3不同计算模型比较与结果分析

利用PKPM软件,结合西安市长安区实际情况,模拟高层框剪结构在相同风荷载作用下,计算模型含地下结构、不含地下结构及其周边不同回填土相互约束作用这三种情况对框剪结构的刚度和承载力影响规律;模拟随结构总高度的变化,分别对比分析计算模型含地下结构时和不含地下结构时,结构刚度和承载力的变化规律。

3.1　计算简图

图5为计算时结构模型示意图。模型一:不含地下室的框剪结构。模型二:地下室水平位移完全约束(取m=-3)。模型三:地下室水平位移无约束(取m=0)。模型四:地下室水平位移约束适中(m=30)。模型五:地下室水平位移约束较大(取m=100)。m为土层水平抗力系数的比例系数,取值范围一般在2.5~100之间,若为一负数m,其绝对值大于或等于地下室层数,则认为有m层地下室无水平位移。

为了便于叙述,假定五种工况:工况①,不含地下室;工况②,m=-3;工况③,m=0;工况④,m=30;工况⑤,m=100。结构模型在地下室周边回填土的不同约束和相同荷载作用下的计算结果见表1和表2。

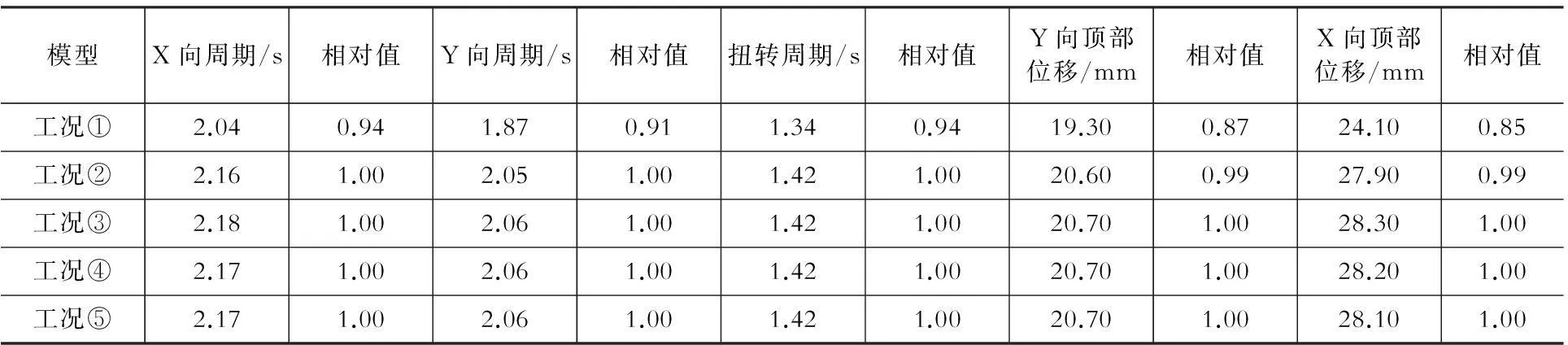
表1　不同工况下的计算结果Table 1　Calculation results under different working conditions

注:相对值指工况①、工况②、工况③、工况⑤的值分别与工况④的相应值之比。

表2　土层抗力系数的比例系数m取不同值时各层刚度值Table 2　Different scale factor m of soil resistance coefficient corresponding to the stiffness of each floor　kN/m

注:相对值指m=-3,m=30,m=100刚度值分别与m=0的刚度值之比。

图5　结构模型图Fig.5　Structure models

3.2　相同荷载作用下计算结果分析

以工况④为参考,由表1可知,模型X向、Y向及扭转周期中,工况①最小,相对值为0.94,工况②-⑤变化较小,相对值为1.0;X向与Y向结构顶点位移中,工况①最小,工况②顶点位移与工况③、④、⑤相比偏小,但差距较小,仅为0.1 mm左右。由此可知,由于工况①完全约束,因此,X向、Y向及扭转周期值小,X向与Y向顶点位移值也小。工况②-⑤考虑了地下室及其周边不同回填土对结构受力的影响,虽然工况③对上部框剪结构约束比工况④小,工况②、⑤对上部框架结构约束比工况④大,但这四种工况顶点位移和周期偏差较小。

在新版SATWE软件中,是用“土层水平抗力系数的比例系数m”来反映地下室周边回填土对结构的约束程度。由表2可知,当m=-3时,地下室刚度刚值最大,是m=0时相应地下层刚度的数千倍;当m为正值时,从地下一层至地下三层,结构刚度逐渐增大,并且随着m值的增加,相应地下层刚度的增加更加显著;对于地上结构,参数m的变化对地上各层刚度影响均较小。

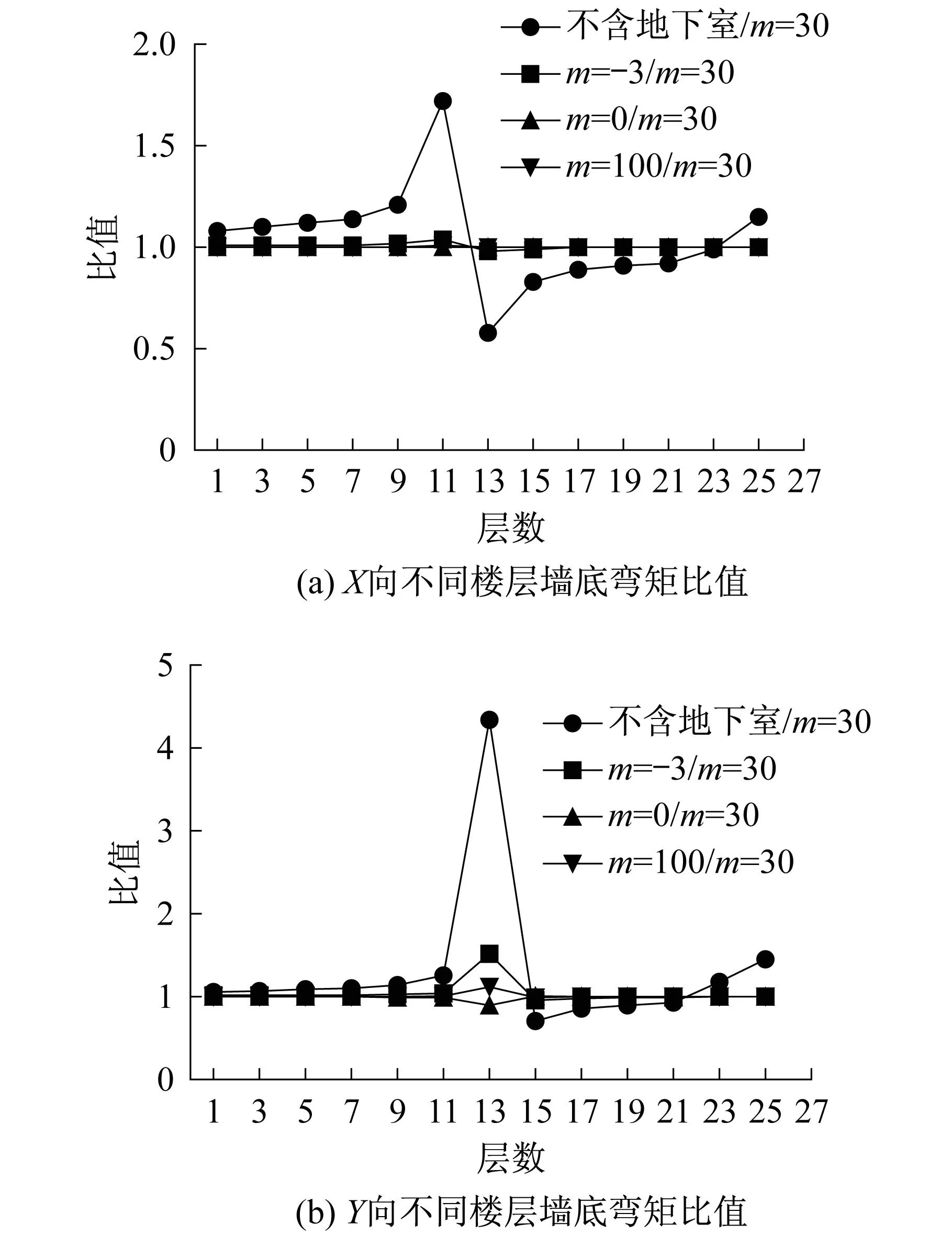
图6　不同楼层墙底弯矩比值Fig.6　Different floor wall bottom bending moment ratios

图6为不同楼层墙底弯矩比值。由图6可知,11层以下工况①墙底弯矩比工况②-⑤相应弯矩大,并从底层开始偏差逐渐增大,12层处弯矩偏差达到最大,比值浮动为0.5左右;13层至22层墙底弯矩比工况②-⑤相应弯矩小,并且偏差逐渐缩小; 23层至25层工况①与工况②-⑤墙底弯矩相比,偏差又逐渐增大,而工况②-⑤墙底弯矩在12层有偏差外,其他层墙底弯矩差距较小。图7为不同楼层柱底弯矩比值。由图7可知,工况①各层柱底弯矩从底层至顶层均小于工况②-⑤柱底的相应弯矩,而工况②-⑤之间柱底弯矩只有底层有较小偏差外,其他各层相应柱底弯矩均相等。

不同总高度的结构顶部水平位移变化百分比公式:

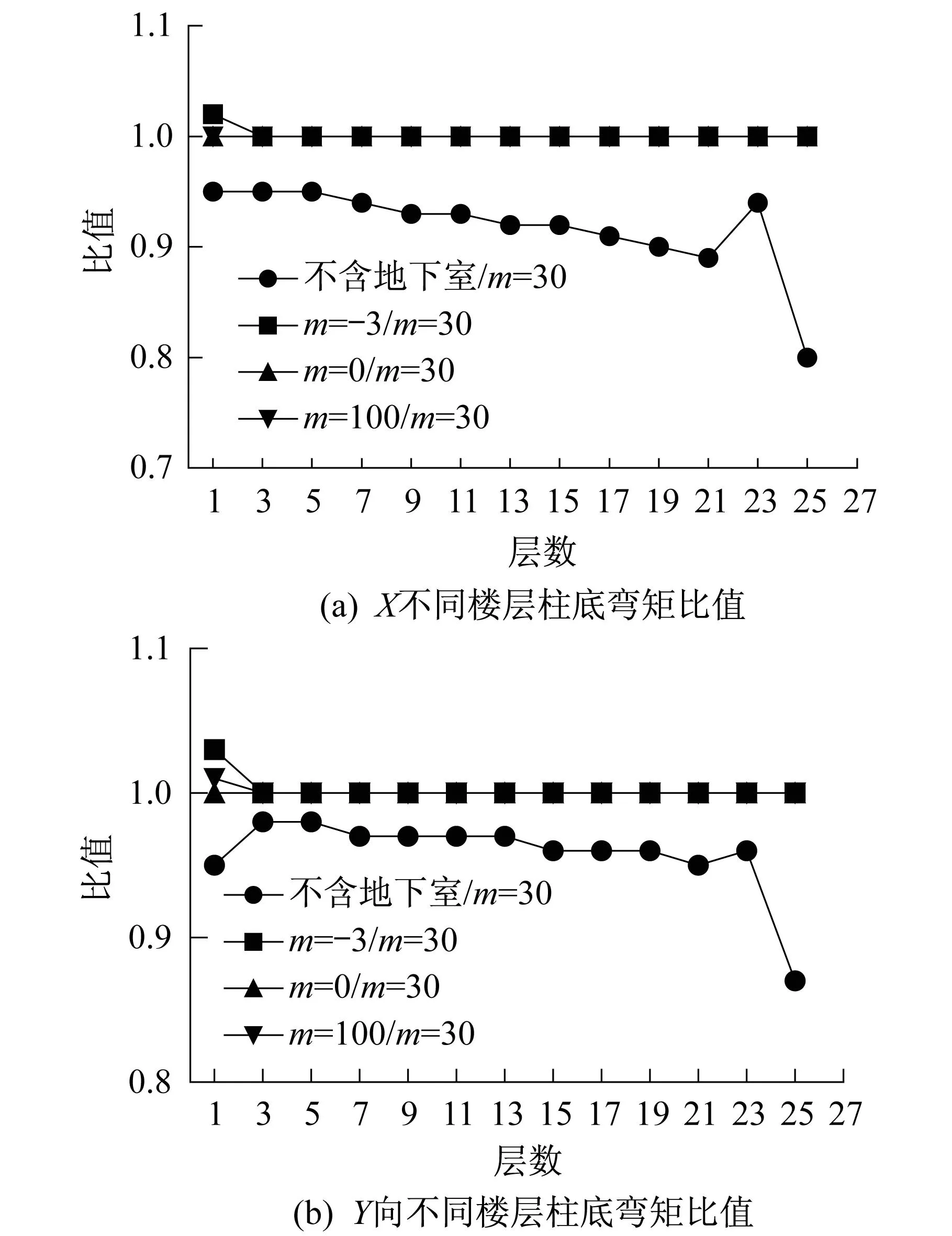
图7　不同楼层柱底弯矩比值Fig.7　Different floor column bottom bending moment ratios

(15)

式中,i为改变模型楼层数后的结构总层数(i=11,12,13,…,33)；j为不同工况(j=2,3,4,5)；uij为结构总层数为i、工况j时结构顶部水平位移值；βij为结构总层数为i、工况j时结构顶部水平位移相对工况1时结构顶部水平位移变化百分比。

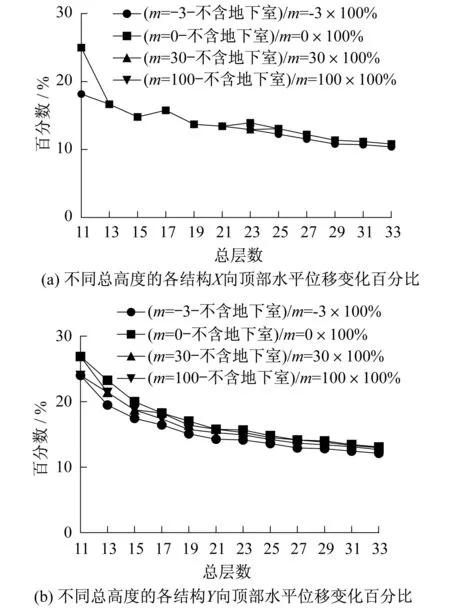
图8　不同总高度的各结构顶部水平位移变化百分比Fig.8　Horizontal displacement variation at different heights

在不改变框剪结构平面布置和构件截面尺寸情况下,计算得到不同总高度的各结构顶部水平位移变化百分比如图8所示。由图8可知,总层数为i层时,不同工况下的βij值差距较小;总层数为11层时,不同工况下βij值约为25%;总层数为33层时,不同工况下βij值约为12%,即结构总层数越少,βij值越大,随着结构层数的增多,βij值逐渐降低。由此可知,结构总高度越低,计算模型不含地下室相对含地下室时计算出的结果差距越大;随着结构总高度逐渐增加,计算模型含地下室时计算出的结果与不含地下室时计算出的结果差距在逐渐缩小。

4结论

通过上述分析,针对嵌固端在地下室顶板处的高层结构得到以下结论:

(1) 不论地下结构刚度多大,实际建筑结构建模计算分析都宜带地下结构(地下结构范围较大时,只需带相关范围),否则计算出的结构整体刚度偏大,与实际情况相差较大,会造成建筑材料无谓的浪费。

(2) 带地下室的高层结构建模计算分析时,宜考虑周边回填土对地下结构刚度和承载力的影响,但回填土对上部结构的刚度和承载力影响较小,建模分析时应酌情考虑。

(3) 在相同荷载作用下,由含地下室与不含地下室的两种计算模型,计算出不同楼层墙底弯矩相比,底部和顶部弯矩差距小,中部弯矩差距较大;计算出的不同楼层柱底弯矩相比,不含地下室结构模型计算的弯矩从底层到顶层均偏大。

(4) 结构高度越低,含地下室与不含地下室结构计算模型计算出的结果差距越大。

参考文献

[1]徐培福,王翠坤,肖从真.中国高层建筑结构发展与展望[J].建筑结构,2009,39(9):28-32.

Xu Peifu,Wang Cuikun,Xiao Congzheng.Development and prospect of high-rise building structures in China[J].Building Structures,2009,39(9):28-32.(in Chinese)

[2]陈仲颐,叶书麟.基础工程学[M].北京:中国建筑工业出版社,1990.

Chen Zhongyi,Ye Shuling.Foundation engineering[M].Beijing:China Architecture and Building Press,1990(in Chinese)

[3]李亚明,张晖,郝安民.超高层建筑筒中筒结构体系之探讨[J].结构工程师,2013,29(6):49-53.

Li Yaming,Zhang Hui,Hao Anming.Discussion on the tube-in-tube structural system of super high-rise building[J].Structural Engineers,2013,29(6):49-53(in Chinese)

[4]Liu C H.Analysis of a cracked beam-column on an elastic foundation[J].2000,13(6):273-279.

[5]张星.人防地下室门框墙荷载取值和内力计算方法[J].结构工程师,2014,30(6):1-9.

Zhang Xing.Load determination and internal force calculation methods for the door frame wall in civil air defense basement structures[J].Structural Engineers,2014,30(6):1-9.(in Chinese)

[6]傅翼,陈春梅.带地下室高层建筑结构计算方法及相关软件的应用探讨[J].沿海企业与科技,2009,111(8):148-151.

Fu Yi,Chen Chunmei.Calculation method and software introduction of the high-rise building with basement[J].Coastal Enterprises and Science and Technology,2009,111(8):148-151.(in Chinese)

[7]中华人民共和国住房和城乡建设部.JGJ 3—2010高层建筑混凝土结构技术规程[S].北京:建筑工业出版社,2010.

Housing and Urban- Rural Development of the People’s Republic of China.JGJ 3—2010Technical specification for concrete structures of tall building[S].Beijing:China Architecture and Building Press,2010.(in Chinese)

[8]杨晓峰,李亮.带地下室高层结构嵌固端假定适用条件研究[J].结构工程师,2011,27(1):66-72.

Yang Xiaofeng,Li Liang.Research on requirement of application for fixed end assumption of high-rise buildings with basement[J].Structural Engineers,2011,27(1):66-72.(in Chinese)

[9]杨晓峰,李亮,瞿海雁.带地下室高层结构侧移及内力计算方法理论研究[J].建筑刚结构进展,2010,12(3):32-36.

Yang Xiaofeng,Li Liang,Qu Haiyan.Theoretical study on calculating methods of the lateral displacements and internal forces of the high-rise building with basement[J].Progress in Steel Building Structures,2010,12(3):32-36.(in Chinese)

收稿日期：2015-04-16

*联系作者， Email:412169225@qq.com