挡土墙主动土压力理论与有限元理论分析比较

孙　超　史迪菲　原利明

(吉林建筑大学测绘与勘查工程学院，长春　130118)

挡土墙主动土压力理论与有限元理论分析比较

孙超史迪菲原利明

(吉林建筑大学测绘与勘查工程学院，长春130118)

摘要：本文根据朗金主动土压力理论，通过研究弹性半空间体内的应力状态，根据土的极限平衡条件得出的土压力计算方法.利用大型通用软件ABAQUS计算挡土墙主动土压力，并与朗金土压力理论下的主动土压力进行比较，说明不同模型选取对试验结果的影响.

关键词：弹塑性；挡土墙；朗金主动土压力理论

挡土墙作为防止土体坍塌的构筑物广泛应用于房屋建筑、水利、铁路以及公路和桥梁工程中.由于挡土墙的土压力计算十分复杂，目前计算多采用古典的朗金(Rankine，1857年)和库伦(Coulomb，1773年)土压力理论[1].随着当前有限元类软件发展日新月异，大型通用软件ABAQUS基于弹塑性理论对主动土压力理论的研究迅速发展，许多理论模拟可以通过计算得到，从而达到节省人力、物力的目的.因此，利用ABAQUS土压力拥有广泛地发展前景.

1模型及相关参数

1.1　Mohr-Coulomb模型与界面接触模型[2]

土的Mohr-Coulomb破坏条件为：

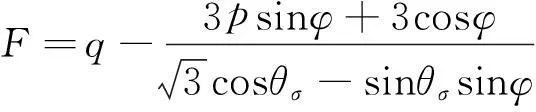
(1)

式中：p与q分别为平均应力和广义偏差应力；θσ为应力Lode角；c与φ分别为土的粘聚力和内摩擦角.

将总应变速率分解为弹性应变速率{εe}和塑性速率应变{εp}两部分：

(2)

其中，弹性应变速率与塑性应变速率分别由广义Hook定律和塑性流动法则确定，即

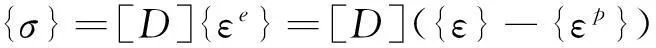
(3)

(4)

综合考虑上列各式，采用塑性一致性条件，得到下列弹塑性本构方程：

(5)

式中：[Dep]为弹塑性系数矩阵，在塑性加载条件下

(6)

而在卸载与中性变载条件下，[Dep]=[De].

挡土墙与土体在刚度上存在较大差异，其交界面会产生相对滑动.因此，在有限元数值分析中，挡土墙和土体之间设置接触类型为表面与表面接触，接触属性为切向行为，摩擦公式定义为罚函数算法，摩擦系数μ=0.001.

1.2　朗金土压力模型

朗金土压力理论通过研究弹性半空间体内的应力状态，根据土的极限平衡条件而得出的土压力计算方法，适用于挡土墙墙背竖直光滑，填土面水平.根据朗金土压力理论，当土体中某点处于极限平衡状态时，大小主应力σ1和σ3应满足以下关系式：

粘性土：

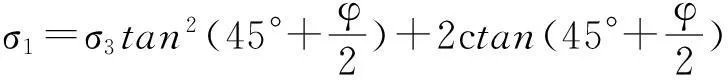
(7)

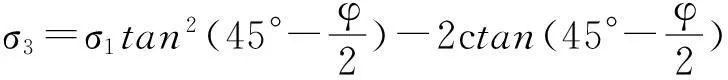
(8)

设墙背竖直光滑，填土面水平，当挡土墙偏离土体时，墙背土体中离地表任意深度z处竖向应力σz为大主应力σ1，σx为小主应力σ3，故可得朗金主动土压力强度σa为：

粘性土：

(9)

1.3　有限元计算模型

有限元方法的基础是变分原理和加权余量法[3]，其基本求解思想是把计算域划分为有限个互不重叠的单元，在每个单元内，选择一些合适的节点作为求解函数的插值点，将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式，借助于变分原理或加权余量法，将微分方程离散求解.采用不同的权函数和插值函数形式，便构成不同的有限元方法.

对于挡土墙和土体，采用8节点平面应变单元C3D8R;挡土墙墙高7m，顶部宽0.6m，底部宽1m，墙背竖直，光滑，墙后填土面水平，并作用有均布荷载q=200kPa，挡土墙示意图见图1，各土层物理力学指标见表1.

图1 挡土墙示意图

表1 各土层物理力学指标

2朗金主动土压力理论，ABAQUS模拟弹性、弹塑性主动土压力强度结果及分析

2.1　朗金主动土压力强度计算结果

通过计算，杂填土顶面处的土压力强度为81.20kPa，杂填土底面处的土压力强度为107.66kPa，粉质粘土顶面处的土压力强度为91.57kPa，粉质粘土底面处的土压力强度为119.96kPa.

2.2　ABAQUS弹性模型、弹塑性模型[4]主动土压力强度计算结果

通过模型模拟结果，弹性理论下杂填土顶面处的土压力强度为17.24kPa，粉质粘土底面处的土压力强度为148.79kPa，见图2.弹塑性理论下杂填土顶面处的土压力强度为17.84kPa，粉质粘土底面处的土压力强度为164.35kPa，见图3.

图2 弹性主动土压力应力云图　　　　　图3 弹塑性主动土压力应力云图　　　　　图4 压应力随深度变化曲线

2.3　朗金主动土压力理论、ABAQUS弹性模型、弹塑性模型主动土压力强度分析比较

通过应力云图可以得出结论，土在弹塑性状态下的压应力与土在弹性状态下的压应力相比要小，挡土墙在主动土压力作用下的应力云图与理论基本一致，压应力最大值发生在挡土墙外表面与土接触的部位.通过受力分析可知，这是由于主动土压力作用在挡土墙下表面上部三分点处，对挡土墙底产生力臂受压所致.

通过图4比较各应力曲线可以看到，土在弹塑性与弹性两种不同状态下的对挡土墙压应力变化曲线形状基本一致.在埋深较小时，与朗金理论不同的是地表压应力值，随着深度的加大，三条曲线开始靠近，在土层变化处开始出现差别，土在弹性状态下的压应力增量逐渐加大，弹塑性状态下的压应力增量开始减小，但基本上呈线性增长，与朗金主动土压力理论一致.由此可知，对土体的研究应采用弹塑性模型，这样所得的结果偏保守，比较安全.

3结论

通过建立弹性模型和弹塑性模型，在相同的条件下模拟，可以得出如下结论：

(1) 朗金理论计算得到的主动土压力偏保守，弹塑性理论和弹性理论计算得到的主动土压力有所增加；

(2) 弹性理论模型和弹塑性理论模型的压应力基本一致；

(3) 弹性模型下的主动土压力应力值大于弹塑性模型下的主动土压力应力值；

(4) 弹塑性理论的计算结果更接近于工程实际.

参考文献

[1] 赵明华,俞晓.土力学与基础工程[M].武汉:武汉理工大学出版社,2009:124-129.

[2] 费康,张建伟.ABAQUS在岩土工程中的应用[M].北京:中国水利水电出版社,2010:67-70.

[3] 崔春义,李顺群,奕茂田,赵颖华.基于ABAQUS的连续墙支护深基坑开挖弹塑性数值分析[J].岩土工程学报,2008(S1):86-90.

[4] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006:86-98.

Retaining Wall Active Earth Pressure Theory and the Theory of Finite Element Analysis

SUN Chao，SHI Di-fei，YUAN Li-ming

(SchoolofGeometricsandProspectingEngineering,JilinJianzhuUniversity,Changchun,China130118)

Abstract：Rankine active earth pressure theory through the study of stress state,the elastic half space body root soil conditions of limit equilibrium of soil pressure calculation method.The common software ABAQUS is used to calculate active earth pressure of retaining,with Rankine earth pressure theory of active earth pressure under comparison,to illustrates the influence of different selection model on the test results.

Keywords:elastic-plastic；retaining wall；rankine active earth pressure theory

中图分类号：TU 413

文献标志码：A

文章编号：2095-8919(2015)06-0019-03

作者简介：孙超(1978~)，男，黑龙江省东宁县人，副教授，博士.

收稿日期：2015-01-14.