城市轨道交通系统的适用性评价
2015-02-18左忠义
左忠义,李 鑫
(大连交通大学 交通运输工程学院,辽宁 大连 116028)*
0 引言
随着我国城市化发展的加速,人们对于出行需求大幅增加,加之私家车数量的极速增加,城市的交通拥堵问题十分严重.结合城市自身特点建设适合的公共交通,优先发展公共交通是解决城市拥堵问题的最佳途径.城市轨道交通系统是一种运量大、快速、安全、环保节能的城市公共交通系统,同时对改善出行条件,引导城市局部发展方面做出很大贡献,因此已经广泛应用于国内外的许多城市.但是由于各个城市的自然条件、经济条件以及已经建成的公共交通水平都各不相同,那么到底什么样的城市适合轨道交通的发展是现在所面临的问题.因此本文对城市轨道交通的适用性问题进行研究,从而能够客观合理的进行城市轨道交通的建设.
目前对于适用性的评价方法常用的有层次分析法、模糊综合评价法等,应用这些方法进行评价时并不能克服实验过程的随机性和主观性.因此本文采用BP神经网络的评价方法,可以有效的避免上述评价方法的不足,客观公正的对轨道交通的适用性进行评价,保证轨道交通合理、适度的建设.
1 城市轨道交通适用性分析
交通系统的适用性[1-4]具体体现在服务方面、成本方面、环境影响方面和社会环境影响方面.城市轨道交通的适用性就是指城市轨道交通技术设备,运营条件等满足城市居民使用的能力,让城市轨道交通与城市之间相互适应,达到整体条件下的最优.城市轨道交通的适用性要求城市轨道交通的建设与城市整体规划的要求相适应,与环境的发展和维护相适应,并且建设施工过程中的安全因素也制约着城市轨道交通的适用性.
2 基于BP神经网络城市轨道交通适用性评价模型的构建
2.1 BP 神经网络
BP神经网络的全称是反向传播学习算法模型(Back-Propagation Network),它是人工神经网络当中应用最广泛的网络模型之一,同时也体现了人工神经网络当中最最核心的部分.BP神经网络完整的理论是由 Rumelhart· Hinton 与 Williams[5]提出的,它是由输入层、输出层和隐含层构成的多层前向网络,其具体的结构图如图1所示.

图1 BP神经网络简化结构图
根据图可以看出,各层与各层之间采用的是全互连方式,而同层单元之间则无相互连接.输入的信号从输入节点输入传递到隐含层节点,然后传向输出层,每一层的节点输出只影响下一层节点的输出.
BP神经网络在进行科学实验的时候,对于网络层数的选取,神经元个数的确定,传递函数的确定以及选择什么样的训练算法,都没有具体的选择参考标准,因此只能通过大量的实验来确定.由于计算量很大,所以采取计算机和相关的软件代替人工进行实验计算.神经网络工具箱(Neural Network Toolbox)简称NNT,该工具箱中包含了很多神经网络常用的模型,还涵盖很多常用的学习算法,并且计算机软件的计算速度远远高于手工计算,因此本文在进行城市轨道交通适用性评价时就是采用的MATLAB软件中的神经网络工具箱进行实验.
2.2 BP神经网络评价模型中评价指标体系的确定
根据城市轨道交通系统的特点进行分析总结,结合城市轨道交通适用性的相关概念,在评价指标建立规则的指导下,建立了影响城市轨道交通的适用性的评价指标体系[6],对大连市能否建设轨道交通进行验证评价.由于沈阳、哈尔滨和长春与大连规模相当,并且都属于东北三省,相互之间存在着一定的竞争关系,所以也将它们三个城市加入到样本的验证.相关的指标数值如表1所示.
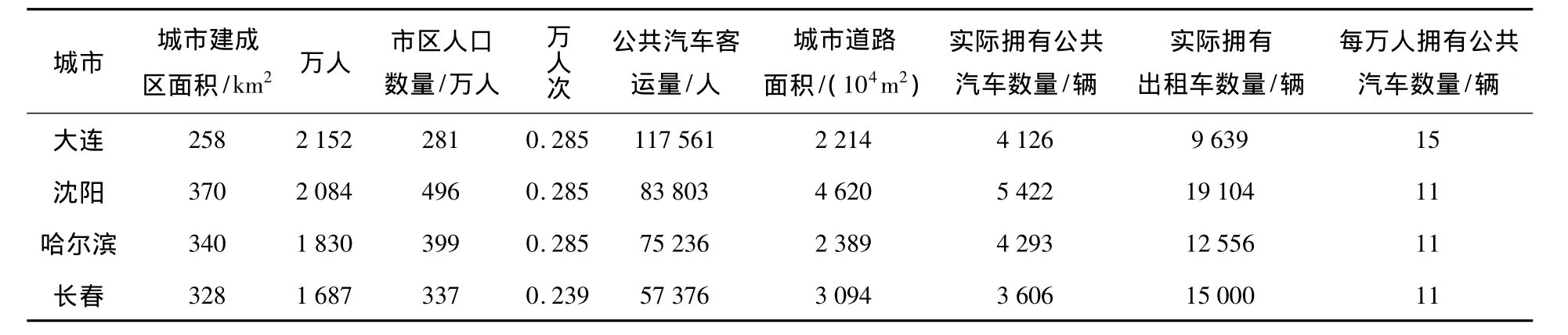
表1 相关城市的评价指标数值
2.3 BP神经网络的构建
本文运用MATLAB软件中的newff函数进行BP神经网络的构建.那么在MATLAB中newff的调用命令如下:

Net为BP网络的生成对象;PR表示维的输入矢量中介于每维的输入的最大值与最小值之间的范围;[S1S2,…,Sn]表示BP网络的N层神经层中每层的神经元的数量;{TF1TF2,…,TFn}表示BP网络的N层神经层中每层的传递函数;BTF表示BP神经网络使用的训练函数;BLF表示权值和阀值的学习算法,PF表示性能函数.
针对本研究要解决的实际问题,对BP神经网络评价模型的具体构建如下:
(1)神经网络的层数的确定
已经有相关的理论证明:只有一层隐含层的神经网络系统能够应用任意精度来表示任意的连续函数,也就是说使用三层的神经网络就可以完成任意精度的任意n维到m维的映射.因此本论文的神经网络确定的层数为三层.
(2)传递函数的确定
BP神经网络中提供了三种传递函数,分别是非线性logsig传递函数、非线性tansig传递函数和线性purelin传递函数.经过以前学者的研究得出,一个具有两层的神经网络,如果第一层选取logsig函数,而第二层选取例如purelin的线性函数就可以模拟任何连续有界的函数.因此确定logsig函数为隐含层的传递函数,确定purelin函数为输出层的传递函数.
(3)训练函数的确定
根据表2可以看出traingd训练函数、traingda训练函数、traingdm训练函数、traingdx训练函数都需要进行了5000次的训练,并且得到的收敛精度也是比较低的.而trainlm训练函数只用了29次训练就达到了的收敛精度,所以选择trainlm函数作为训练函数.

表2 不同训练函数的训练结果
(4)训练参数的确定
确定训练函数为trainlm,根据上面的实验可以得出trainlm的训练次数较少,所以确定BP神经网络的最大学习次数为1 000,网络的最大允许误差为0.000 01,这些参数的设定在MATLAB中采用的函数是net.trainParam函数来进行的,那么具体的调用命令如下:

(5)各层的神经元个数的确定
输入层的神经元个数是通过建立的评价指标体系来确定的,本文以9作为输入层的神经元个数.而以1作为输出层的神经元个数.因此对于各层的神经元的个数的确定,主要是指隐含层的神经元的个数确定.根据本论文第三章中的第三小节中的公式,可以计算出隐含层的神经元个数的范围是在5~13之间.
本研究采用实验的方法来确定隐含层的神经元个数,其中设定训练次数为1 000,目标精度为0.000 01,以神经元个数5为例,其它的数值只是对命令中的神经元个数进行替换,调用命令如下:

根据表3可以得出,训练次数并不是随着神经元个数的增加而减少,收敛精度与神经元的个数也不是成规则的反比关系.最终通过整体数据可以得出,当隐含层的神经元个数为10时,它的训练次数最少为6次,收敛精度较高,故选择10个隐含层神经元.

表3 神经元个数数值表
综上所述,本研究构建的BP神经网络为为三层神经网络,它们分别是输入层、隐含层和输出层.输入层神经元个数为9个,隐含层神经元个数为10个,输出层神经元个数为1个.隐含层的传递函数为logsig函数,输出层传递函数选择为purelin函数,训练函数定为trainlm函数.最大学习次数为1000次,最大允许误差定为0.00001.所以调用命令为:

建立的BP神经网络的结构图如图2所示:

图2 建立的BP神经网络结构图
2.4 BP神经网络的仿真应用
对于BP神经网络训练后的网络需要进行仿真,本文选用MATLAB中的sim函数进行仿真训练.Sim函数的调用命令如下:
[Y,Pf,Af,E,perf]=sim(net,P,Pi,Ai,T)其中:Y表示网络输出;Pf表示训练终止时的输入延迟状态;Af表示训练终止时的层延迟状态;E表示输出和目标矢量之间的误差;Perf表示网络的性能;
Net表示要仿真的神经网络;P表示网络的输入;Pi表示输入延迟的初始状态;Ai表示层延迟的初始状态;T表示目标矢量.
由于在进行BP神经网络实验的时候,将输入的数据都进行了归一化处理,因而对于输出的数据也是已经归一化处理后的数据,为了更好的跟原始数据进行比较,需要将归一化的输出数据进行还原.运用MATLAB中的postmnmx调用命令进行数据还原,具体调用命令如下:
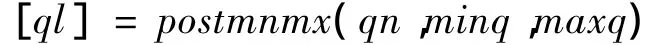
3 实例分析
运用建立的BP神经网络在MATLAB中进行大连市的实例验证时,同样要进行样本的归一化处理,在此采用的归一化处理函数为tramnmx函数;验证完成后,对于输出的结果,需要进行反归一化处理,采用的调用函数为postmnmx函数.那么在MATLAB软件中具体的验证调用命令如下:
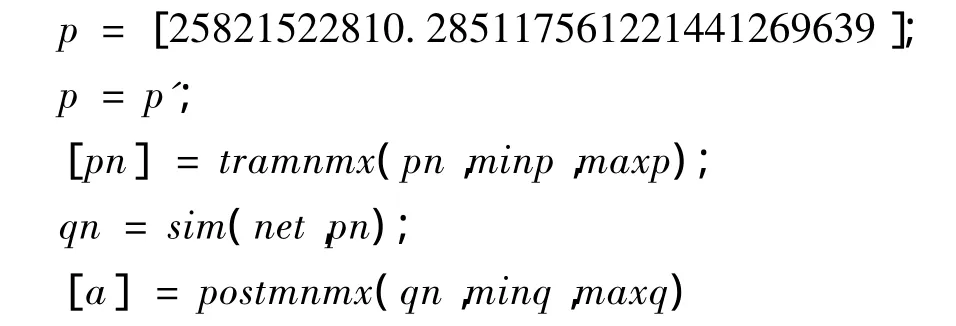
将上文建立的综合评价指标输入,建立的神经网络的输出数据如表4所示.

表4 神经网络的输出结果
如果城市的各项评价指标在MATLAB软件中通过神经网络运算出的结果接近1,则说明轨道交通适用于该城市;如果运算输出的结果接近0,则说明轨道交通不适用于该城市.根据表4的输出结果可以得出,四个城市的输出结果都接近数字1.因此可以得出结论,城市轨道交通适用于沈阳、哈尔滨、长春和大连四个城市的城市建设.
4 结论
本文采用的BP网络进行城市轨道交通适用性的评价分析是科学可行的,得出的结论也是可信的.通过BP神经网络计算输出的结果与实际情况相符,证明了该模型的准确性,可以进行实际应用.与此同时在大连市建设城市轨道交通能够缓解城市的拥堵,减轻传统公共交通的压力,提高乘客的服务水平,推动城市的未来发展.并且大连市在经济、技术、客流等方面都具备建设城市轨道交通的实力.
通过运用BP神经网络进行城市轨道交通适用性的评价,可以科学的评判轨道交通是否适用于该城市.这样就可以合理有效的推进城市轨道交通的建设与发展,从而避免超前或者滞后建设.对于不具备建设轨道交通的城市,可以通过其他的方式缓解城市的交通问题,如建设公交专用道、提高公共交通服务水平等方法.
[1]张琦.新型轨道交通系统在上海的适用性分析[J].交通与运输:学术版,2013(2):101-104.
[2]秦武.空中轨道交通系统的适用性分析[J].城市公用事业,2012(6):17-21.
[3]张生,魏涛,彭燕.长沙 BRT系统适用性研究[J].湖南交通科技,2004(1):109-112.
[4]徐伟.海口市快速公交系统适用性分析[J].福建建设科技,2013(2):80-82.
[5]Barnard.Optimization for training neural nets[J].IEEE Trans.On Neural Networks,1992,3(2):232-240.
[6]中国城市统计年鉴2006年[M].北京:中国统计出版社,2006.
