物流中心选址的区间可拓评价模型

2015-02-18吴华伟

物流技术 2015年8期

刘静，吴华伟

（1.湖北文理学院机械与汽车工程学院，湖北襄阳 441053；2.汽车零部件制造装备数字化湖北省协同创新中心，湖北襄阳 441053）

1 引言

随着信息技术和现代管理理论的发展，物流管理得到了越来越多的重视，而物流中心的分布对现代物流活动有着重大影响，其合理选址将能减少货物运输费用，从而大大降低运营成本，因此，规划物流中心的选址是一个重要的决策问题[1]。目前，物流中心选址方案的评价方法很多，其中模糊评价法应用最为广泛[2]。与经典的评估方法相比，模糊评价法虽有它的优点，但也存在极值掩盖、信息丢失与最大隶属度原则不适用等不足[3]。可拓学是由中国学者蔡文教授首创、近30年来形成和发展起来的一门新的数学理论。该理论能很好地处理多参数、矛盾的、不相容的问题，且推理过程严密、运算工作量小，因而广泛应用于综合评价[4]及优化决策[5]等领域。然而其在理论上仍存在一些不完善的地方，导致其在评价过程中具有局限性。

由于客观事物的复杂性、不确定性及人类思维的模糊性，决策者往往难以用精确的数值来描述评级指标的信息量[6]。在这种情况下，用区间数来表示评价指标取值是个很好的选择。故应用可拓法进行综合评价时，用区间数来描述物元特征量值更符合实际。尽管如此，基于区间物元的可拓评价法在物流系统综合评价领域的应用还没有相关研究文献。同时在物流中心选址评价时，指标权重对于评估结果有着重要影响。通常的主观赋权法有较大的主观随意性，而客观赋权法基本没有反映评价主体的偏好，两种赋权法都具有一定的局限性。为了物流中心选址评价时赋权更加科学，评价结果更加真实，本文提出了基于决策者偏好和赋权法一致性的方法，对客观赋权与主观赋权进行集成，使指标的赋权达到主观和客观的统一。

2 预备知识

在经典数学中，点x与点y的距离已有定义，即

在传统的可拓学理论中，设x为实域(-∞,+∞)上任意一点，[bL,bR]为实域上任意有限区间，则：

称ρ(x,[bL,bR])为点x与区间[bL,bR]的距离。

为了建立区间上的关联函数，必须引入区间与区间的距离。设[xL,xR]与[bL,bR]为实数域上的任意有限区间，则：

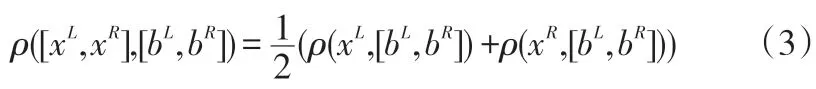
ρ([xL,xR],[bL,bR])称为区间[xL,xR]与区间[bL,bR]的距离[7]。

3 区间可拓决策模型

3.1 问题描述

某物流中心选址的多指标决策问题，有s个备选方案，记为方案集N={N1,N2,…,Ns} ；m个指标，记为指标集C={C1,C2,…,Cm}；指标Cj(1 ≤j≤m)的权重为wj(1 ≤j≤m)，且有0 ≤ωj≤1，ω1+ω2+…ωm=1；试应用区间可拓学理论确定选址方案。

3.2 物元模型定义

可拓学以物元理论作为其理论框架，物元[8]是可拓学认识世界的基本逻辑细胞,它将现实事物抽象为事物、特征及事物关于该特征值的量值所组成的一个三元组,记作R=(N,C,V)。其中，N表示方案，C表示评价指标，V表示N关于C的区间量值，这三者称为物元的三要素，其物元的表达式记为：

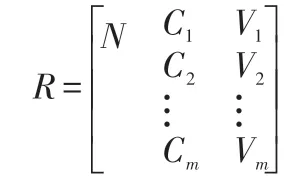
则备选方案集N关于评价指标集C的区间数决策矩阵为：

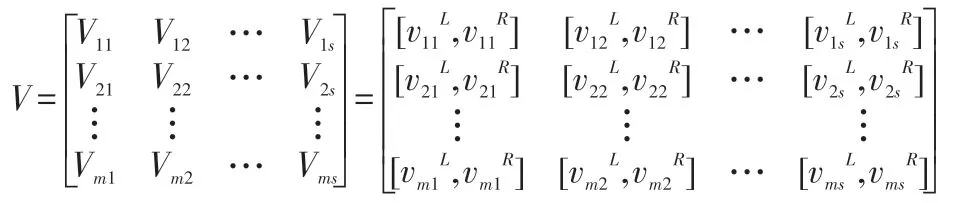
3.3 确定经典域与节域

在确定了评价模型物元表达式的基础上，就可以根据衡量条件确定期望方案（理想方案）的物元模型为：

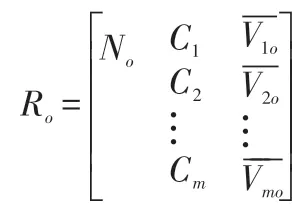
式中：为理想方案No关于指标Cj的区间范围，即经典域；记为指标Cj所能容许的量域，即节域，其可根据每个特征指标的可能最大量值范围来确定，显然有⊂Vjp。

3.4 关联度

根据区距可计算关联度：

式（4）中Ki(Vji)表示评估方案Ni与理想方案No关于评价指标Cj的关联度。

3.5 确定权系数

传统的可拓评价方法在确定指标权重时，一般采用主观赋权法或者客观赋权法。主观赋值法主要考虑专家的知识和经验，赋值大小容易受决策者意向和偏好的影响，主观随意性较大；而客观赋值法虽然比较客观，但很难反映专家的知识和决策者的意见，甚至有时得到的权重与实际完全不符。鉴于此，本文采用文献[9]中提出的基于决策者偏好和赋权法一致性的组合赋权法，将客观权重和主观权重相融合。组合权重W=(ω1,ω2,…,ωm)用以下公式确定：

式（5）中：

W(k)=(ω1(k),ω2(k),…,ωm(k))—表示第k种赋权法所得到的指标权重值；

q—表示赋权方法的个数；

θ—决策者对某赋权法的偏好度在确定组合权重时的相对重要性，θ的取值视具体决策问题而定；

1-θ—该赋权法与其它赋权法的一致性程度在确定组合权重时的相对重要性；

λk—决策者对第k种赋权法的偏好度，满足λk≥0(k=1,2,…,q)且=1，λk可采用AHP法确定；

βk—第k种赋权法的相对一致性程度，满足βk≥0(k=1,2,…,q)且

易知W为归一化向量，其具体计算过程如下：

（1）利用Kendall 协和系数检验法对各赋权法所得权重的一致性进行检验，如果通过一致性检验，则利用计算组合权重，如果没有通过一致性检验，则转步骤（2）；

（2）应用式（6）计算第k种赋权法与第f种赋权法的Spearman等级相关系数ζkf。

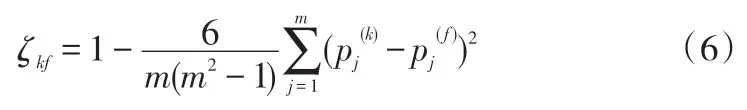
式（6）中，pj(k)表示第k种赋权法中指标Cj(1 ≤j≤m)的权重在该赋权法所得权重向量中的排序号，pj

(f)含义相同。（3）计算第k种赋权法的平均一致性程度，其计算公式为：

（4）归一化处理，即：

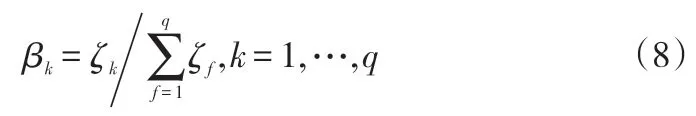
（5）利用式（5）可得组合权重向量W。

3.6 优度计算

评估方案Ni的优度为：

由于优度是反映物流中心选址备选方案接近期望方案（理想方案）的度量，关联度越大，则该备选方案就越接近期望方案，即该方案越佳。

4 实例分析

以某制造企业确定最优的物流中心方案为例。首先利用定量模型求得3 个待评备选方案，方案集N={N1,N2,N3}；并制定了6个考核指标C={C1,C2,…,C6}，分别为网络运作成本C1、网络服务能力C2、网络稳定性C3、网络柔性C4、网络拓展能力C5及网络节点所在地的经济、政治与资源状况C6。

步骤1：构建方案集N对评价指标集C的区间数决策矩阵为：

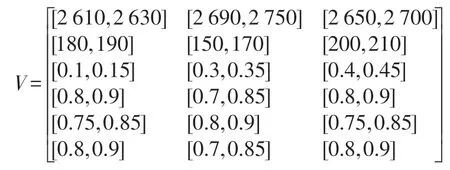
步骤2：根据市场竞争的要求和企业自身状况，给出经典域和节域：

步骤3：计算关联度。利用式（2）-（4），可计算出各待评方案的关联度，见表1。

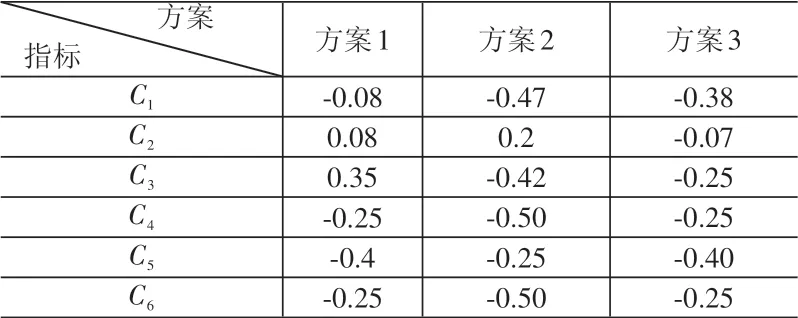
表1 待评方案的关联度

步骤4：确定权系数。采用基于决策者偏好和赋权法一致性的组合赋权法来确定综合权重，其中三种赋权法分别为熵权法、AHP法、Deiphi法，θ=0.5，则各指标权重的计算结果见表2。

步骤5：优度计算评价结果判断。根据表1、表2 和式（9）确定待评的3 个选址方案优度，结果为K1=-0.11 ，K2=-0.37，K3=-0.29。

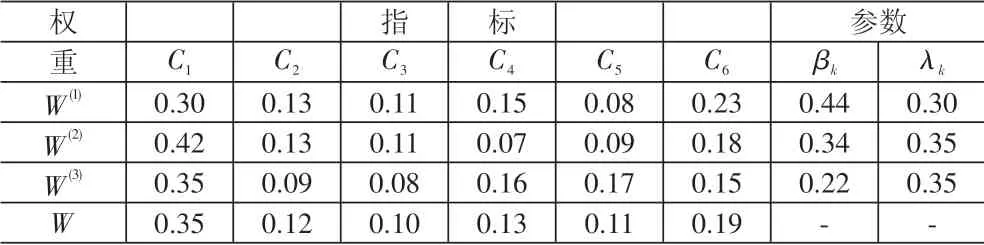
表2 组合权重计算表

确定全体方案优劣序：N1＞N3＞N2，即方案1为最佳方案。

步骤6：结果验证。为了验证区间可拓评价模型的可行性与有效性，本文将运用灰关联评价方法对案例进行评价，并将二者的评价结果进行比较。灰关联度评价方法的具体评价过程可参考文献[10]，计算可得三个方案的灰关联度分别为0.91、0.74、0.78，即方案1为最优方案，其结果与本文提出的区间可拓评价模型的评价结果相同。由于灰关联度评价方法是一种运用比较广泛的决策评价方法，其可行性已经在众多工程实践中得到了验证，从而验证了本文提出的区间可拓评价模型的可行性与有效性。