基于切割聚类的快速多分量LFM信号分离

刘　凯, 韩嘉宾, 王韵白, 黄青华

(上海大学特种光纤与光接入网重点实验室通信与信息工程学院， 上海 200072)



基于切割聚类的快速多分量LFM信号分离

刘凯, 韩嘉宾, 王韵白, 黄青华

(上海大学特种光纤与光接入网重点实验室通信与信息工程学院， 上海 200072)

摘要：针对多分量线性调频(linear frequency modulation, LFM)雷达信号检测和参数估计精度低、计算速度慢等问题,提出了一种基于小波变换的切割聚类拟合参数估计的算法。该方法首先通过小波变换得到信号的三维时频分布图,其次采用等高线截取提取出小波脊线,再找出脊线的交点,以交点为界对小波脊线图进行切割,利用模糊C均值聚类完成各LFM分量脊线的聚类,最后分别对每段脊线进行拟合加权,从而估计出多分量LFM信号参数。仿真结果表明,与基于Hough变换检测直线方法相比,不仅在计算复杂度以及参数估计的准确度上都有较大的提升,而且当LFM信号分量达到4个以上亦有较准确的检测精度。

关键词：多分量线性调频信号; 参数检测; 小波变换; 聚类; 拟合

0引言

随着雷达电子战逐渐发展成为电子战中的重要组成部分[1],电子战中各式各样的干扰显著降低了雷达的工作性能与探测效率,针对电子战中的干扰,进行雷达信号的分离识别,成为雷达抗干扰技术新的课题与挑战。

线性调频(linear frequency modulation, LFM)信号是一种大时宽-带宽积的信号,由于具有良好低截获性能的,多分量LFM信号被广泛应用于现代雷达领域。各辐射源信号同时到达接收机形成的多分量信号成为重要的研究对象,针对多分量LFM信号未知参数的估计,并进行雷达信号的分离识别,不仅对电子战理论的丰富和发展有促进作用和重要意义,而且对雷达实战具有实质性的推动作用。

多分量LFM信号参数估计方法主要包括时域分析法、频域分析法以及时频分析法[2]。由于LMF信号在时频域中是一条直线,因此时频分析法是LFM信号分选的常用方法。时频分析方法可以分为线性和非线性2种[3]。常用的非线性时频表示有魏格纳-威尔分布(WVD)、乔伊-威廉斯分布(CWD)[4-6]。由于非线性时频分析方法不可避免地存在交叉项干扰,因而限制了其应用。而线性小波时频变换[7-9]具有良好的时频域局部化以及多分辨的特性,又适合用于处理大时宽-带宽积的信号,因此小波变换被广泛的应用于对信号的脉内细微特征提取中。

LFM信号具有时频域是一条曲线的特性,所以在时频域提取信号的特征问题可以转化为检测小波脊线图像中的直线问题。作为图像处理和模式识别领域的一个重要环节,直线检测最常用的方法是Hough变换[10]。由于传统的Hough变换存在计算量大,占用内存大、检测性能受制约、不能检测出直线段的完整信息的缺点。为了解决上述问题,文献[11]提出了一种基于距离约束的随机Hough变换直线检测算法,一定程度提升检测直线的速度,有效减少了存储空间;文献[12]提出一种自适应的PHT算法,通过比较涵盖像素点的不同区域的差别检测直线,有效地减少了直线检测的计算量;文献[13]提出一种快速随机Hough变换多直线检测算法,通过对边缘像素点的梯度方向信息做统计来确定直线的主方向,有效地解决了无累积问题,并且能够检测直线段的完整信息；文献[14]提出一种联合独立分量分析(ICA)和Wigner-Hough变换的方法,能够在低信噪比的情况下,实现多分量LFM信号的分离。

总体来说,这些方法都是基于Hough变换的直线检测,都得将时频图像转换到参数空间,再进行直线估计,并且对小波脊线图进行参数估计时,基于Hough变换的直线检测方法会随着LFM信号分量的增加或者多LFM信号分量的参数比较接近,会导致直线检测的性能急剧下降。据此,本文在多分量LFM信号小波时频变换的基础上,以信号的小波脊线图作为图像,提出了一种切割聚类拟合算法,首先对脊线图像进行切割聚类处理,再对数据进行直线拟合,进而估计出直线参数。仿真结果表明本文提出的方法能够有效的提出多分量LFM信号的参数,在速度以及性能上都有了很大的提升。

1多分量LFM信号模型及小波变换

1.1多分量LFM信号模型

多个LFM信号叠加构成了多分量LFM信号,其信号模型可以表示为

(1)

式中，Ai是信号幅度; f0i是信号载频;ui是信号调制指数。从式(1)得知,估计出每个信号的这3个参数就能实现对信号的分离。为简化信号模型,模型中每个子信号的幅度都相等。

1.2LFM信号小波时频分析

小波基的选取关系着信号时频特性的好坏,所以应选取时频域特性都比较好的小波函数,Morlet小波基具有较好的时频聚集性,且为渐近性信号。Morlet小波函数表达式为

(2)

其傅里叶变换为

(3)

若信号的采样率和小波的采样率相同的话,小波尺度与频率之间的关系是:α=f0/fx,其中，α为伸缩尺度,f0为采样率;式(2)中,u为尺度加权因子,它决定了Morlet小波的窗口大小;ω0为小波变换的基频;α对应频率为ω0/α。由式(3)可得Morlet小波的中心频率在ω=ω0/α处。

对于任意采样信号s(nTs)=Aexp(-jω1nT),则信号的Morlet小波变换定义为ω(α,nTs),Ts为采样周期。

(4)

式中,⊗表示卷积。

由式(4)可得信号经小波变换后幅值的模为

(5)

由式(5)可知,当ω0/α=ω1时,|ω(α,τ)|取得最大值。即函数|ω(α,τ)|在ω0/α=ω1处取得最大值,这表明信号在频率ω1上能量最集中。通过信号的小波变化,便可求得信号幅度A。

2基于切割聚类拟合LFM信号分离

2.1检测直线数量

直线数量虽然不属于LFM信号参数,但却是估计各条不同直线参数的基础。本文把重采样之后的小波时频变换数据WT(α,n)作为待处理的数据,设第ti时刻的小波变换模值为|WT(α,ti)|,则在时刻ti,如果:

(6)

则|WT(α,ti)|为第ti时刻的极大值。遍历整个采样时间轴,在每个时间点上找出其极大值个数Num,则脊线数量为

L=max(Num)

(7)

2.2检测脊线交点

不同调制斜率的LFM信号分量的小波脊线必定会有交点,由于交点的影响,使得直线参数估计的计算复杂度和困难程度都有所增加,所以本算法估计直线参数之前,首先对脊线进行预处理,将信号小波变换后的数据分成若干个类,减小甚至避免脊线交点所带来的问题。分类的准则是以脊线交点(时间)为基准,对时频区域进行分割。若交点个数为n,则聚类分割的区域数量为(n+1)。假设第ti时刻检测到脊线数量为Li,如果满足:

(8)

则Li所在的位置即脊线相交的交点Pi。遍历整个时频区域,找出所有脊线交点P,根据P的位置将时频区域分割成不同的块。图1为对小波脊线图进行时间切割的示意图。

图1　脊线切割示意图

2.3FCM聚类算法

切割分段避免了交点对直线检测的影响,但是不同直线的数据仍然会导致直线参数估计偏差大的后果,为了减小这种影响,本文运用模糊C均值聚类算法对每段数据进行聚类,使得属于同一条直线的数据尽可能聚为一类,为准确估计出直线参数打下坚实的基础。

模糊C均值(fuzzyC-means,FCM)聚类[15],是一种目标函数法,是模糊聚类算法中运用最多的算法。设样本空间X={x1,x2,…,xn},将X分为k(k>1)类,FCM算法是将目标函数F(u,C)最小化的迭代收敛过程,其目标函数F(u,C)定义为

(9)

式中，u=(uij)为模糊矩阵,表示第i个样本xi隶属于第j个聚类中心cj的隶属度值,m是模糊加权指数,经验取值范围为[1,5]。

运用拉格朗日乘数法求目标函数F(u,C)的最小值,可求得uij和Cj的值。不断迭代求解新的隶属度函数和聚类中心,直到目标函数达到最小值,完成聚类。

2.4最小二乘直线拟合

直线参数估计的目的得到各个LFM分量信号的未知参数,运用直线拟合方法对聚类之后的数据进行拟合,完成对各LFM分量的参数估计,本文采用的是最小二乘拟合算法。令需要拟合的直线函数关系为

y=kx+b

(10)

式中，2个待估计参数k代表直线斜率；b代表截距。

对于待估计数据(xi,yi)(i=1,2,…,N),用最小二乘法估计参数时,要求观测值yi的偏差的加权平方和为最小,即

(11)

2.5直线加权

对于同一区域而言,拟合出的直线参数互不相同,但对于不同的区域段拟合出的直线可能是属于同一条直线,故需要对直线进行去重处理,本文采用了加权去重处理方法。

假设不同的段所占时间跨度分别为{t1,t2,t3,…,tn+1},假设第ti个段中某条直线的参数为{ki,bi},第ti+1个段中的某条直线为{ki+1,bi+1},若2条直线的参数差值小于阈值,则认为2个线段属于同一根直线,则新的直线参数为

(11)

3多分量LFM信号分离流程

综上所述,针对多分量LFM信号检测和参数估计,本文算法的总体流程如图2所示。

图2　多分量LFM分离流程图

4实验仿真结果分析

为了验证提出方法的有效性,本文采用4个LFM雷达辐射源信号作为分析对象。信号的采样率为1GHz/s,带宽B为200MHz,载频为300MHz,信号所占频带:300～460MHz,4个LFM信号调制指数k分别为:1012Hz/s、3012Hz/s、2012Hz/s、512Hz/s,延迟时间τ(信号的起始位置)分别为:0μs、2μs、4μs、3μs,信号持续时间为max{B/k+τ},信噪比(signal-to-noiseratio,SNR)为5dB。

Morlet小波的基频ω0=25MHz,尺度加权因子u=100,小波变换尺度α=0.988i(i=1,2,…,50),i为尺度变换等级数。利用式(5),对多分量LFM信号做小波变换。设小波变换|ω(α,τ)|的最大值为max,取小波脊线的门限Threshold=0.7max,画出|ω(α,τ)|≥Threshold在二维坐标ω0/α、τ下的时频等高线,如图3所示。

图3　时频等高线图

得到小波脊线图后,根据脊线交点对脊线图进行切割,完成对数据的分块处理。图4给出的是对信号脊线图分段完之后,对该区域内线段的点的聚类图,聚类特征为原数据与数据均值之差以及原数据与数据均值之差的开方。从图中可以看出,本文提出的算法能够很好的对不同直线段的数据进行分类,为估计直线参数打下良好的基础。

图4　不同直线数据聚类图

图5给出的是针对2条直线,本文算法和Hough变换算法直线检测比较的效果图。实验结果验证了本文提出的算法较Hough变换检测直线算法有优势,本文算法能更好的逼近原LFM信号小波时频等高线,估计的误差更小,直线检测精度越高。

图5　两条直线拟合图

当LFM信号分量增多时,Hough变换检测脊线参数的性能急剧下降,以至于不能准确的检测出直线的个数,而本文提出的算法能够更好的抑制交叉干扰,其检测直线的精度较传统的Hough变换也有较大的提升。图6显示的是当LFM分量增加到4个时,在直线数据聚类之后,运用本文提出的算法进行直线参数的估计以及直线检测,从图中可以看出本文提出的直线检测算法能够较好的估计出多分量LFM信号的调制信息。

表1和表2给出了在不同分量LFM信号的情况下,本文提出的直线检测算法和Hough变换检测直线算法的性能比较。随机产生不同分量的LFM信号,并做50次实验。表1给出的是调制指数k的平均误差率,表2给出的是相对延迟时间t的平均误差。从表中可以得知,Hough变换在检测1～2根直线的时候性能还较好,但当直线数量在3根以上的时候,其估计误差骤增,甚至无法准确有效地估计出直线的参数;而本文提出的算法在直线数量增加的情况下,仍能保持较好的估计性能。在LFM信号分量达到4个,平均误差率并没有骤降,其调制斜率的平均误差在2.3%以内,时延(信号的起始位置)的相对平均误差在0.3μs以内,实验结果表明本文算法能把估计误差控制在一个很小的范围之内,能较准确地估计出直线的参数。

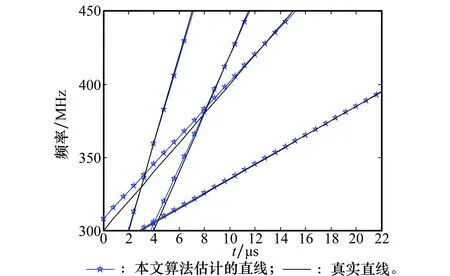
图6　分段拟合结果图

%

表2　相对延迟时间平均误差　μs

为了验证本算法检测直线的快速性,分别分析了Hough变换检测直线算法和本文算法直线分离的计算复杂度,其结果如表3所示。M为角度θ在[0,π]间均匀的取值个数,可以将小波脊线图看做n×n个像素点的二值图像进行处理,L为Hough变换检测峰值个数,Ln为将直线段连接成直线的复杂度。N为采样数据点数,本文算法复杂度包括判断直线数量N,分段N,聚类N,拟合N。实际运行时间为实现2个LFM信号的分离的时间,仿真实验中n2≈N。从表中可以看出本文算法的运行速度有了明显的提升,进一步满足了工程上的实时性。运行算法的计算机配置为acer4 750 G(2.5G的酷睿i5处理器,4G内存)。

表3　不同算法的时间复杂度

5结论

LFM信号是现代雷达领域运用较多的信号形式,基于小波变换的切割聚类拟合直线检测算法,在提取信号小波变换的脊线时频图的基础上,结合FCM和直线拟合算法,减少了直线估计的计算量,有效解决了在多分量LFM信号的情况下,传统Hough变换无法正确检测直线的难题,仿真结果表明本文提出算法的有效性,并具有一定的工程应用价值。

参考文献：

[1] Li Y M, Wang F H, Huang Z T, et al. Performance of anti radiation seeker in counteracting three uncorrelated decoys[J].SystemsEngineeringandElectronics,2011,33(3):500-505.(李益民,王丰华,黄知涛,等.反辐射导引头抗非相干三点源性能分析[J].系统工程与电子技术,2011,33(3):500-505.)

[2] Bian H L. The research of some problems in nonstationary signals time-frequency joint analysis methods and application[D]. Chengdu:University of Electronic Science and Technology,2008.(边海龙. 非平稳信号联合时频分析方法的若干问题研究与应用[D]. 成都:电子科技大学, 2008.)

[3] Yin X Z, Yu S L. Time-frequency analysis theory and its application[J].ModernElectronicTechnique, 2006, 29(21):118-120.(殷晓中, 于盛林. 信号的时频分析理论与应用评述[J]. 现代电子技术, 2006, 29(21):118-120.)

[4] Yao J J, Yang L M, Feng J G. Application of common time-frequency analysis methods in analyzing characteristic quantity of digital seismic wave[J].JournalofNorthwesternSeismological, 2011, 33(2):105-110.(姚家骏, 杨立明, 冯建刚. 常用时频分析方法在数字地震波特征量分析中的应用[J]. 西北地震学报, 2011, 33(2):105-110.)

[5] Huang Y, Liu F, Wang Z Z, et al. Periodic FRFT-based multi-component LFMCW radar signal separating[J].ActaAeronauticaetAstronauticaSinica, 2013, 34(4):846-854.(黄宇,刘锋,王泽众,等.基于周期FRFT的多分量LFMCW雷达信号分离[J].航空学报,2013,34(4):846-854.)

[6] Zhang L M, Zhong Z G, Wang Z Z, et al. Detection and separation of overlapped quasi-LFMCW signals based on periodic WHT recurrent filter[J].ActaAeronauticaetAstronauticaSinica, 2013, 34(11):2580-2589.(张立民, 钟兆根, 王泽众, 等. 基于周期 WHT 循环滤波的交叠类似 LFMCW 信号检测与分离[J]. 航空学报, 2013, 34(11):2580-2589.)

[7] Le B, Liu Z, Gu T. Weak LFM signal dectection based on wavelet transform modulus maxima denoising and other techniques[J].InternationalJournalofWavelets,MultiresolutionandInformationProcessing, 2010, 8(2):313-326.

[8] Li Q, Wang Q. Wavelet spectrum and its application to LFM signal detection[J].ChineseJournalofQuantumElectronics, 2005, 5:103-108.

[9] Li L, Si X C, Chai J F, et al. Parameters estimation for LFM radar signal based on reassigned wavelet-radon transform[J].JournalofSystemsEngineeringandElectronics, 2009, 31(1):74-77.(李利,司锡才,柴娟芳,等.基于重排小波-Radon变换的LFM雷达信号参数估计[J].系统工程与电子技术,2009,31(1):74-77.)

[10] Chung K L, Chang T C, Huang Y H. Comment on:extended hough transform for linear feature detection[J].PatternRecognition, 2009, 42(7):1612-1614.

[11] Zeng J X, Wang B B, Chen Z L. Random Hough transform lines detection based on the distance constraint[J] .JournalofNanChangHangKongUniversity(NaturalSciences),2011,25(3):7-11.(曾接贤,王斌斌,陈志良.基于距离约束的随机Hough变换直线检测算法[J].南昌航空大学学报(自然科学版),2011,25(3):7-11.)

[12] Matas J, Galambos C, Kittler J. Robust detection of lines using the progressive probabilistic hough transform[J].ComputerVisionandImageUnderstanding,2005,78(1):119-137.

[13] Zhang J X, Shen X L, Wang H, et al. Fast multi-line detection algorithm using randomized hough transform[J].JournalofZhe-jiangUniversityofTechnology,2013,41(3):346-350.(张江鑫,沈小兰,王辉,等.快速随机Hough变换多直线检测算法[J].浙江工业大学学报,2013,41(3):346-350.)

[14] Qiang G, Ya J L, Chang H W, et al. Novel detection method for multi-component LFM signals[C]∥Proc.ofthePervasiveComputingSignalProcessingandApplications,2010:759-762.

[15] Krinidis S, Chatzis V. A robust fuzz local informationC-means clustering algorithm[J].IEEETrans.on,Image Processing, 2010,19(5):1328-1337.

刘凯(1981-),男,副教授,博士,主要研究方向为盲信号处理、通信信号处理、室内无线定位、雷达信号处理、雷达信号分选。

E-mail:liukai@shu.edu.cn

韩嘉宾(1990-),男,硕士研究生,主要研究方向为雷达信号分选、雷达信号处理。

E-mail:jiabinhan@126.com

王韵白(1990-),女,硕士研究生,主要研究方向为雷达信号分选。

E-mail:wangyunbai@yeah.net

黄青华(1978-),女,副研究员,博士,主要研究方向为阵列信号处理、盲信号处理和3D音频。

E-mail:qinghua@shu.edu.cn

网络优先出版地址：http:∥www.cnki.net/kcms/detail/11.2422.TN20141105.1633.009.html

Fast separation of multi-component LFM signals based on

segmented clustering

Liu Kai, Han Jia-bin, Wang Yun-bai, Huang Qing-hua

(KeyLaboratoryofSpecialtyFiberOpticsandOpticalAccessNetworks,ShanghaiUniversity,

SchoolofCommunicationandInformationEngineering, 200072)

Abstract:To solve the problems of low precision and slow computation speed in the multi-component linear frequency modulation (LFM) radar signals detection and parameter estimation, a novel parameter estimation algorithm with segmented clustering and fitting based on wavelet transform is proposed. Firstly, the 3D time-frequency distribution image of the signals is obtained by the wavelet transform, and extracts the wavelet ridge of the signals with the contour interception algorithm. Then find the intersection of the ridge, and cut the image of the wavelet ridge based on the intersection. After that, all the ridges of the LFM signals are clustered by FCM algorithm. Finally, each segment is fitted and weighted respectively and the parameters of the multi-component LFM signals are estimated. Simulation results show that the computational complexity and the precision of the parameter estimation notonly have greatly improved, but also have more accurate precision under the condition that LFM components reach more than four when compared with the traditional Hough transform for the line detection.

Keywords:multi-component linear frequency modulation (LFM) signals; parameter detection; wavelet transform; clustering; fitting

作者简介：

中图分类号：TN 958

文献标志码：ADOI:10.3969/j.issn.1001-506X.2015.05.04

基金项目：上海市科委(15ZR1415500)资助课题

收稿日期：2014-06-11；修回日期：2014-10-23；网络优先出版日期：2014-11-05。