广义指数与麦克斯韦分布的尾部性质

黄建文，刘衍民，罗国旺

(遵义师范学院 数学与计算科学学院,贵州 遵义 563002)

广义指数与麦克斯韦分布的尾部性质

黄建文，刘衍民，罗国旺

(遵义师范学院 数学与计算科学学院,贵州 遵义 563002)

研究了广义指数与麦克斯韦分布的累积分布函数以及概率密度函数渐近的尾部性质。尤其当自由度参数以适当的方式趋于正无穷时，考虑了广义指数和t分布(类似地对于麦克斯韦和t分布)概率密度函数(累积分布函数)比值的渐近性质。作为推论，得到了广义指数与麦克斯韦分布的Mill’s率，且举例说明该结果在极值理论中的应用。

广义指数分布；麦克斯韦分布；Mill’s率；t分布；尾部性质

1 研究背景

由于广义指数与麦克斯韦分布是比广义伽马分布更加简洁和灵活的广义伽马分布子族的两个模型，因而它们在经济研究和持续时间分析中得到越来越多的关注，详细介绍参见文献[1]。

广义指数分布(generalized exponential distribution)是在1999年由Gupta 和 Kundu[2]定义的。广义指数分布主要的应用领域为生存分析、产品的寿命分析、可靠性工程和地球信号时频分析等。同时，发现广义指数分布使用非常灵活，能够代替著名的伽马、韦伯或者对数正态分布，可十分有效地用于分析正的寿命数据[3-4]。同时，广义指数分布也有一个漂亮的物理解释：假设在一个并联的系统中有n个元件，并且每个元件的寿命分布是独立同分布的，如果每个元件的寿命分布是广义指数分布，则这个并联系统的寿命分布也是广义指数分布。

广义指数随机变量的概率密度函数是

(1)

其中α,λ>0。令Gλ,α(·)表示相应的累积分布函数，当参数α=1时，它就退化为指数分布(或寿命分布)。

麦克斯韦随机变量的概率密度函数为

(2)

其中σ>0。令Mσ(·)表示相应的累积分布函数。麦克斯韦分布从化学到物理有很多应用领域，尤其是在统计动力学中。此外，其应用领域还包括分子的速度、接近热力学平衡的理想气体、量子效应、非相对论速度、描述动量和分子能量的分布等。

Finneretal[5]研究了当自由度以适当的方式趋于正无穷时，相比于正态分布t分布的尾部性质。他们得到了一些成果，包括t分布的密度函数比值的渐近性质、大偏差定理和渐近的Mill’s率。关于某些指定分布的尾部性质最近受到极值统计领域专家和学者的关注和研究。彭作祥等[6]研究了广义误差分布的尾部性质，并且得到相应的渐近Mill’s类型率。蔺富明和彭作祥[7]讨论了短尾对称分布的尾部性质，并且得到了相应的独立同分布随机变量序列最大值的极限分布。蔺富明和蒋英英[8]考虑了广义短尾对称分布，并且得到了相应的渐近尾部性质、Mill’s率和部分最大值的渐近分布。廖昕等[9]研究了对数偏正态分布的尾部性质、次指数性和极值分布。

Mills[10]给出了概率密度函数为φ(x)的正态分布函数Φ(x)下面的不等式和Mill’s率:对于x>0,

(3)

当x→∞时，

(4)

为了得到主要结果，需要以下定理：

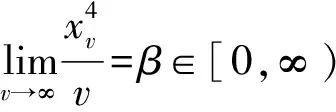
(5)

其中fv(xv)和Fv(xv)分别表示自由度为v的t分布的概率密度函数和累积分布函数。

2 广义指数分布的尾部

对于固定的v,λ和α,很容易验证:当x→∞时,

(6)

因此，下面将讨论当t分布的自由度以适当的方式趋于无穷时，相比于t分布，广义指数分布的尾部性质。

定理2 对于x>0，假设v=v(x),λ=λ(x)，使得

(7)

成立。对于固定的α>0,则

(8)

证明 注意到

(9)

并且

(10)

(11)

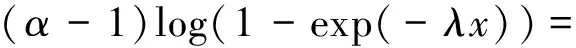
再结合式(11)，即可完成对定理2的证明。

定理3是相应的大偏差定理。

定理3 在定理2的条件下，有

(12)

证明 给出t分布的一个结果[11]：对于所有的x>0和v>0，有

(13)

利用式(7)，则有

(14)

其中

注意到

(15)

结合式(13)和(14)，则有

(16)

再由定理2以及式(7)可知定理3得证。

推论1 在定理2的条件下，有

(17)

注记1 式(4)，(5)以及式(17)给出的Mill’s率对于一些经济和金融数据的尾部性质研究是非常重要的，而且风险率(或失效率)与Mill’s率的倒数是一致的。

3 麦克斯韦分布的尾部性质

定理4 令σ=σ(x),v=v(x)，使得

(18)

则对于x>0,有

证明 注意到当v→∞时，

(19)

并且

(20)

结合式(19)，定理4得证。

对于t分布和麦克斯韦分布的渐近尾部性质，将给出如下的大偏差定理。

定理5 在定理4的条件下，有

(21)

证明 为了证明定理5,首先给出以下不等式[12]:

(22)

结合不等式(13)和(22)，有

(23)

利用定理4和式(18)，有

(24)

类似地，对于下界，有

(25)

结合式(24)和(25)，定理5得证。

推论2 在定理4的条件下，有

由于

则由推论2可得：当x→∞时，有

因此，由文献[13]的命题1.18，有Mσ∈D(Λ)。

以下推论给出的Mσ(-x)分布表示的是推论2另一方面的应用。

推论3 在推论2的条件下，对于充分大的x，则有

其中：

证明 由推论2以及基本计算过程，结论得证。

注记3 在推论3中给出的Mσ(-x)分布的表示的一个直接应用是表明：对于σ>0，Mσ∈D(Λ)，参见文献[13]中的推论1.7。也可以考虑麦克斯韦分布规范化最大值的一致收敛速度(来自于文献[13]第2.4.2部分)和大偏差性质(来自于文献[13]命题2.10)，而辅助函数f(t)在这些研究中起着重要的作用。除此之外,推论3的重要应用是得到最优的规范化常数βn，满足

并且αn=f(βn)，使得对于n>n0,有

其中C1

[1] MORTEZA K,ALIREZA A.Some properties of generalized gamma distribution[J].Math Sci Q J,2010,4(1):9-28.

[2] GUPTA R D,KUNDU D.Generalized exponential Distributions[J].Austral and New Zealand J Statist,1999,41(2):173-188.

[3] GUPTA R D.Exponentiated Exponential Family:An Alternative to Gamma and Weibull Distributions[J].Biometrical Journal,2001,43(1):117-130.

[4] GUPTA R D,KUNDU D.Generalized exponential distribution:Existing results and some recent developments[J].J Stat Plan Infer,2007,137(11):3537-3547.

[5] FINNER H,DICKHAUS T,ROTERS M.Asymptotic tail properties of Student’st-distribution[J].Commun Stat Theory Methods,2008,37:175-179.

[6] PENG Z,TONG B,NADARAJAH S.Tail Behavior of the General Error Distribution[J].Commun Stat Theory Methods,2009,38(11):1884-1892.

[7] LIN F,PENG Z.Tail Behavior and Extremes of Short-Tailed Symmetric Distribution[J].Commun Stat Theory Methods,2010,39(15):2811-2817.

[8] LIN F,JIANG Y.A General Version of the Short-Tailed Symmetric Distribution[J].Commun Stat Theory Methods,2012,41(12):2088-2095.

[9] LIAO X,PENG Z,NADARAJAH S.Tail properties and asymptotic expansions for the maximum of the logarithmic skew-normal distribution[J].J Appl Probab,2013,50(3):900-907.

[10]MILLS J P.Table of the ratio:Area to bounding ordinate,for any portion of the normal curve[J].Biometrika,1926,18:395-400.

[11]SOMS A P.Bounds for thet-tail area[J].Commun Statist Simul Computat,1983,12:559-568.

[12]刘豹,付颖.麦克斯韦分布的逐点收敛速度[J].西南大学学报(自然科学版),2013,35(5):80-83.

[13]RESNICK S I.Extreme value,Regular Variation,and Point Processes[M].New York:Springer-Verlag,1987.

[14]LIU C,LIU B.Convergence Rate of Extremes from Maxwell Sample[J].Journal of Inequalities and Applications,2013,2013:477.

(责任编辑 何杰玲)

Tail behavior of Generalized Exponential and Maxwell Distributions

HUANG Jian-wen, LIU Yan-min, LUO Guo-wang

(School of Mathematics and Computational Science, Zunyi Normal College, Zunyi 563002, China)

The asymptotic behavior of the probability density function (pdf) and the cumulative distribution function (cdf) of the generalized exponential and Maxwell distributions were studied. Specially, we considered the asymptotic behavior of the ratio of the pdfs (cdfs) of the generalized exponential and Student’st-distributions (likewise for the Maxwell and Student’st-distributions) as the degrees of freedom parameter approach infinity in an appropriate way. As by products, Mills’ ratios for the generalized exponential and Maxwell distributions were gained. Moreover, we illustrated some examples to indicate the application of our results in extreme value theory.

generalized exponential distribution; Maxwell distribution; Mills’ ratio;t-distribution; tail behavior

2015-10-11 基金项目：国家自然科学基金资助项目(71461027); 贵州省科技基金资助项目(黔科合J字LKZS[2014]29号); 贵州省科技计划课题(黔科合LH字[2015]7001号, 黔科合LH字[2015]7006号)

黄建文(1988—), 男，甘肃甘谷人，硕士研究生，讲师,主要从事极值统计分析研究。

黄建文，刘衍民，罗国旺.广义指数与麦克斯韦分布的尾部性质[J].重庆理工大学学报(自然科学版)，2015(12):147-151.

format：HUANG Jian-wen, LIU Yan-min, LUO Guo-wang.Tail behavior of Generalized Exponential and Maxwell Distributions[J].Journal of Chongqing University of Technology(Natural Science)，2015(12):147-151.

10.3969/j.issn.1674-8425(z).2015.12.025

O211.67

A

1674-8425(2015)12-0147-05