基于蒙特卡罗模拟方法的城市内涝灾害风险分析
2015-02-18邓秉德庞晓波黄妙棋
邓秉德,庞晓波,黄妙棋
(1.吉林大学 商学院,长春130012;2.吉林财经大学 统计学院,长春130117)
0 引言
城市内涝是指在城市区域范围内,由于短时间内降雨强度较大,同时城市地表下垫面的渗透能力、蓄水能力较弱,因而在短时强降雨情况下形成地表径流的一种区域性洪涝灾害。2010年住建部对351个城市开展调查,发现在2008~2010年间有62%的城市发生内涝事件。2013年9月,国务院印发《关于加强城市基础设施建设的意见》,意见中指出:要用10年左右时间建成较完善的城市排水防涝、防洪工程体系。因此完善城市内涝模型,综合运用各个学科的知识和相关数据对城市中某一具体区域发生内涝的风险进行分析和量化是一项重要的课题,这将有利于相关决策部门做出相应的评估和预案。
1 城市内涝致灾因素及简化城市内涝模型
城市内涝的过程简单的说就是降水落到地表,在下渗和排水能力不足的条件下在地面形成径流,地面汇集的水流受到地势的影响向低洼处汇集,从而在地势较低处形成较深的积水,从而造成相应的灾害。因此有必要简单梳理一下城市内涝的成灾因素,并回顾简化内涝模型的主要内容。
1.1 城市内涝致灾因素
城市内涝的发生是多个因素耦合的结果,致灾因素基本如下。
(1)气象因素。连续强降水是最主要的原因,加之近年来极端的天气的频现。此外城市中建筑物密集,汽车与空调等设备排出大量废热,市区与市郊之间形成空气环流从而形成热岛效应。近期研究表明热岛效应会使得市区降水量明显高于郊区,因此市区发生内涝的风险更大。
(2)地面因素。城市建设中柏油路等硬化路面的面积比例逐渐增大,即便是人行路透水砖的使用的也不广泛。这就造成雨水下渗部分减少,相反更有利于雨水在地面形成径流及汇流。
(3)城建设计因素。首先是城市排水系统标准较低。目前市政建设中雨水管渠的重现期一般都设定在0.5~3年,重要地段,重点区域采用3~5年标准。当面对50年或100年一遇的降水时,灾害发生不可避免。其次是雨污分流建设仍然滞后,排水管网堵塞不利于雨水快速排出。最后是暴雨强度公式需要一定程度的修订,对于市区局部易积水点的降水分析,需要根据目前的数据进行修订,这对于相关的路桥、地铁站点、地下停车场的建设有着重要的意义。
1.2 城市内涝模型概述
综合国内外研究的现状,城市内涝模型是针对城市内涝特征建立的模型系统,一般由地面高程模型、降水模型、产汇流模型以及排水模型构成。下面分别概述四个模型的基本功能。
(1)地面高程模型。DEM模型的主要功能是找出易积水点的位置。在GIS系统的支持下,对收集来的地面高程信息进行处理,完成对易积水区域的识别。DEM模型将分析的区域划分为若干栅格,将地面高程数据同地面建筑物信息进行比对处理,排除建筑物、若干孤立较浅区域对低洼区域的判断。公式表达为:

其中i代表行数,j代表列数;Mij代表修改后的栅格单元,Dij代表原地形栅格单元,Hij代表城市中建筑物高度的栅格单元。
(2)降水模型。降水模型描述一次降雨的雨量同降雨重现期、降雨时间之间的定量关系,降水模型基本上由暴雨强度公式就可以完成。公式如下:

i是设计降雨强度(mm/min),TE是设计降雨重现期(a),A1为重现期为1年的设计降雨的雨力,t是降雨历时(min),b、C和n是特定参数。城市内涝多由暴雨形成,因此针对历史数据,可以由降雨量和重现期反向推导出降雨时间,这对于模拟城市内涝过程至关重要。
(3)产汇流模型。产汇流模型描述雨水降落到地面后受到植被截留、蒸发、低洼留存、下渗因素的综合作用,在地表形径流的过程。通常用公式表示:

其中R(t)为在t时刻地面径流深,i为降雨强度,in为植被截留,e是蒸发率,sd是填洼率,f是下渗率。这些因素中植被截留和蒸发通常可以忽略,影响地面径流的最大因素是下渗率。
(4)排水模型。排水模型主要描述道路或建筑物地面下的排水管网实际排水的能力。排水能力的大小主要受到排水管的数量和直径的影响。排水能力应用漫宁公式描述如下:

其中n为管壁粗糙率,w、R、S分别为过水断面面积、水力半径和管底坡度。
2 城市内涝的建模实例
本文的目标在于说明如何在城市内涝模型中运用蒙特卡罗模拟方法评估内涝风险,因此下文以一座下凹式立交桥为例子,以城市内涝模型各模块公式及思想建立相关数学模型。建立的数学模型分析立交桥底内涝的风险而非整个城区内涝的系统模型,模型中的高程数据因涉密而进行简化但不影响整体有效性。下面给出立交桥相关数据及建立的内涝模型。
(1)立交桥及其汇水面积。所选取的立交桥如图1所示,立交桥南北向长530 m,其中上下引道长均为198 m,坡度为3.73%,下穿部分长140 m,下穿主线宽25 m。立交桥排水口13个(下穿部分5根,上下引道各4根)。排水口直径300mm。容易计算立交桥下凹底部的自身汇水面积为1.325hm2,为了分析地面高程变化对汇水面积的影响,考虑到桥两侧辅路宽度也应计算在内,则可以将桥底路面增宽5m或10m,则汇水面积就变为为1.625hm2或1.925hm2,在进行风险模拟时这三组数据将会被用到。
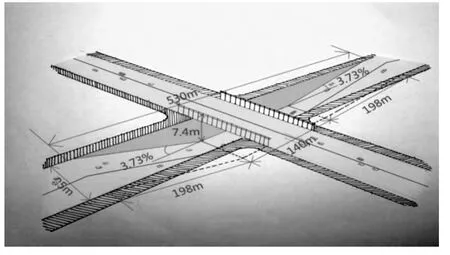
图1 立交桥结构图
(2)降水模型。降水模型采用式(2),查阅《室外排水设计规范》可得北京市暴雨强度公式为:

假设某次降雨满足该城市暴雨重现期的特征时,可利用式(5)近似计算出粗单元格内的总降雨量(m3):

式中t为降雨历时(min),s为汇水面积(hm2),i(t)为设计降雨强度(mm/min)。
(3)排水模型。本次建模中仅考虑路面下方的排水管道,暂不考虑水泵等排水设施,这也与国内多数路桥状况相符。按照简化的模型则排水量计算:

式中:t为降雨历时(min),φ为阻塞系数,Di排水管道直径(mm),Vi为水流速度,k为排水管根数。管道如图2所示。

图2 简化管道示意图
(4)下渗模型。雨水降落到地面,地面材质即下垫面材料对雨水形成径流有较大影响,不同材料的径流系数又是不同的。模型中考虑到道路两侧可以进行绿化,因此有必要计算不同下垫面的径流系数,并计算渗水量。渗水量可以用式(8)计算。

其中:si为粗单元格内第i种垫面所占的面积(m2),s为粗单元格面积(m2),αi(t)为第i种下垫面的雨水径流系数。在模拟分析中,我们应用武晟(2006)所做的实验数据,建立回归模型,可以得到水泥路面的径流系数随时间t的关系为:

经统计检验,拟合效果非常好。
(5)桥底积水深度的计算。
本次建立的数学模型主要分析桥底处的内涝灾害,因此不考虑地面的汇流过程,计算桥底积水深度可以采用“体积法”,即先计算汇集到桥底的降水总量,而后再根据地形特征计算出桥底处的积水深度。综合上面的分析,桥底处汇集的水的体积可以用降水量减去排水量和渗水量,即Qc=Qj-Qp-Qs。将上面的式子综合起来可得:
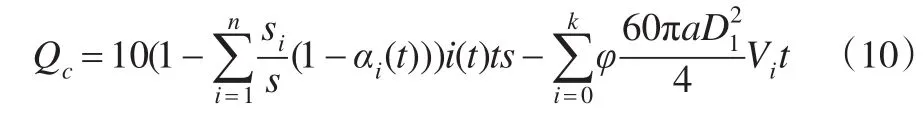
为了简化计算,我们将下凹式立交桥下方的路面特征简化为一个倒三角模型。则可以计算出积水点的积水深度为:

其中H为积水深度,L为道路宽度,Qc为积水体积。
3 运用蒙特卡罗模拟方法分析内涝灾害风险
3.1 蒙特卡罗模拟方法及自助法
简单的说蒙特卡罗方法就是利用计算机中产生的随机数模拟随机变量的各种可能值,将随机变量的各种可能值带入到目标函数中,则可以得到目标函数值的各种可能结果及其分布状况,利用模拟的结果我们可以间接了解目标函数的性质或解决相关问题。应用蒙特卡罗模拟方法需要知道随机变量的总体分布及其参数,但并不是所有目标函数中的随机变量及其分布都是可以获知的,在模拟分析中可以采用自助法来来弥补这一不足。自助法就是对原始样本进行“再抽样”的方法,这种方法要求样本的分布同总体分布高度近似。
3.2 模拟的参数选择
本文中积水深度可以看作是目标函数,则观察式(10)、式(11)不难发现,影响积水深度的变量包括:降雨历时、下垫面比例、堵塞系数、降雨重现期。式(10)、(11)中的其它变量多为确定性变量如排水管径,本次模拟暂不纳入到模拟分析中。在本文的模拟分析中,降雨历时我们利用国家气象信息中心的“中国地面气候资料日值数据集”,具体为1950~2010年北京市的降雨数据。数据集中的数据为降雨量,我们通过java编程并结合重现期将降雨量转换为降雨历时数据。在模拟分析中,我们并不假定降雨历时数据服从何种分布,而是采用自助法为模拟分析提供数据,由于样本中提供了60年的降水数据,因此我们认为样本数据同总体较为近似,符合自助法的要求。下垫面的比例刚好同辅路的绿化水平有关,因此在模拟分析中我们设定汇水面的绿化率为0、14.25%及28.57%,这样我们可以观察绿化率对于内涝状况的影响。本文中堵塞系数用来体现排水管道的堵塞状况,由于城市排水管网受到生活垃圾的影响,堵塞系数暂假定为服从在0.5~0.8的均匀分布,事实上这种设定是较为保守的!降雨重现期是暴雨强度公式中的重要参考指标,为了反映城市中的极端暴雨状况,我们选择5年、10年、25年、50年、100年进行比较分析。
综上介绍了模拟的目标函数及其各个变量的分布状况。为便于说明将主要模型及参数列表如下。
3.3 模型模拟及分析
承上,模拟分析中的目标函数为积水深度,影响积水深度的变量已经简化为为汇水面积、绿化率和重现期。这三个变量代表的更广泛的实际意义为:汇水面积反映的是高程变化对积水深度的影响,绿化率反映的是下垫面材质不同对积水深度的影响,重现期反映的是极端天气的变化对于积水深度的影响。模拟的目的也就在于对比分析上述三个因素对于积水深度的影响程度。上述三个变量均有多个可能值,则模拟结果也会有很多组,为便于分析仅提供下述两组模拟结果:一组为固定汇水面积为1.925情况下绿化率和重现期对积水深度的影响状况;另一组为固定绿化率为0的情形下,汇水面积和重现期对积水深度的影响状况。应用stata软件,每组中的每一种情形都进行1000次模拟运算,计算机会计算出不同参数相互组合下积水的深度值。对模拟出的积水深度进行充分利用,可以让我们认识到积水点的平均深度、内涝阻碍交通的概率等问题。如图3为汇水面积为1.925,绿化率为14.285%,重现期为25的积水深度分布图。
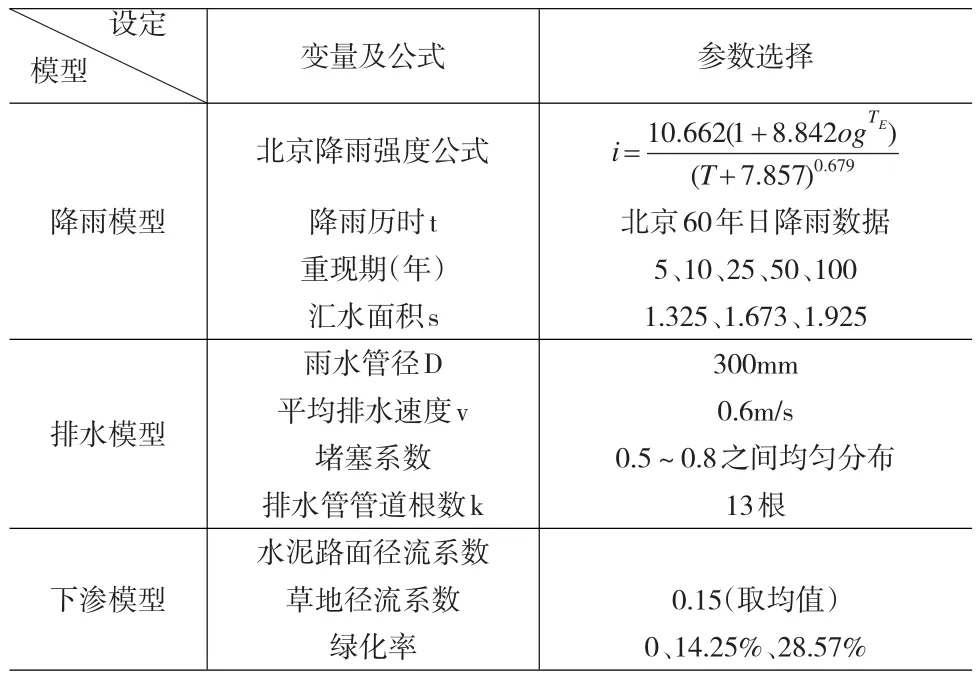
表1 模型参数一览表

图3 积水深度模拟结果示例
类似于图3的模拟结果有很多,将模拟结果进行加工汇总得到表2和表3,这时我们可以观察不同条件下,积水深度均值的交叉表。从两张表中不难发现:固定汇水面积条件下,积水深度同绿化率成反比,同重现期成正比;在绿化率固定的条件下,积水深度同汇水面积成正比,同重现期成反比。
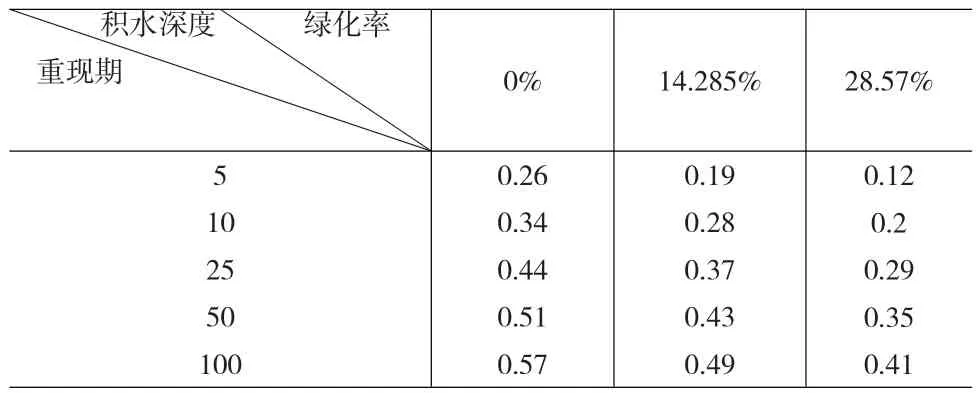
表2 积水面积1.925条件下,积水深度均值一览表 (单位:米)
3.4 内涝对车辆危害的风险分析
表2和表3是对模拟结果的汇总,事实上我们更加关心的直观问题是:根据历史降雨资料,1000次随机的降雨发生在此立交桥处,对交通有何影响?内涝灾害概率有多大?易知乘用车的排气管高度不同在通过积水路段熄火的情况是不同的,可以将城市中的乘用车分为小型车和大型车,设定小型车在积水0.4米时熄火受损,大型车在0.6米水深处熄火受损。将积水深度的模拟结果以0.4米和0.6米为阈值分别进行频数统计就可以得到直观的内涝灾害概率。

表3 绿化率为0条件下,积水深度的均值一览表
(1)固定汇水面积1.925hm2条件下,绿化率和重现期对车辆受损的影响分析。如表4所示,车辆受损概率随绿化率的提高而降低,随重现期的提高而上升。例如绿化率为0,重现期为10的情况下,小车受损概率为24.90%,如果绿化率为14.28%,则车辆受损的概率快速下降到1.90%。这说明对于中等强度的降水,道路两侧的绿化是非常有效的。重现期的提高使得各组绿化率下车辆受损的概率大幅上升,这也说明极端天气的破坏作用非常大。
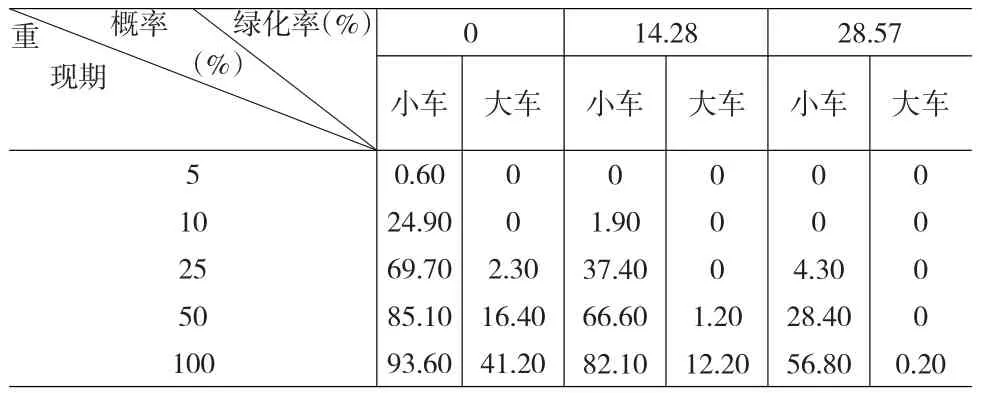
表4 固定汇水面积(1.925hm2),车辆受损概率汇总表
更加直观的观察上表的概率分布情况可以绘制三维柱形图,如图4所示。

图4 车辆受损概率三维柱形图
(2)固定绿化率为0的条件下,汇水面积和重现期对车辆受损的影响分析。如表5所示,车辆受损的概率同汇水面积、重现期成正比。汇水面积的变化其实反映的是模型中地面高程的变化,从表格中可以看到重现期为10年,汇水面积由1.673hm2提高到1.925hm2,面积增大了15%,小型车的受损概率由1%提高到24.90%,从这个例子也可以说明在绿化率为0的区域,汇水面积的增大显著的提高了相关灾害风险的发生。重现期反映了极端天气的作用,观察可知当重现期超过10以后,小车基本上都存在受损的风险,大车状况要相对安全许多。

表5 固定绿化率为0,车辆受损概率汇总表
同上更加直观的观察上表可以绘制三维柱形图,如图5所示。

图5 车辆受损概率三维柱形图
3.5 内涝阻碍交通时间的分析
在模拟计算的过程中已经获得了地面积水量,将下渗模型和排水模型带入,即可以计算出雨停过后地面积水自然排干的时间。将这个时间长度作为阻碍交通的时间的一个度量指标。将上述两组模拟结果分别进行计算可以得到下面的表6。由于没有排水设施等辅助手段,可以看到排干积水需要的时间同绿化率成反比,同重现期和汇水面积成正比。在本例中,中等强度的降雨完全排干积水也要60分钟左右,而百年一遇的降水则要100分钟或甚至更长时间。
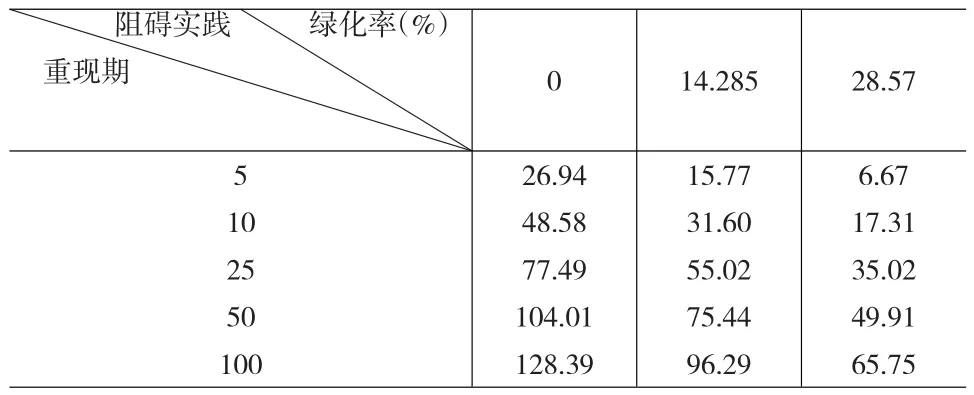
表6 固定汇水面积,阻碍交通时间一览表(分钟)
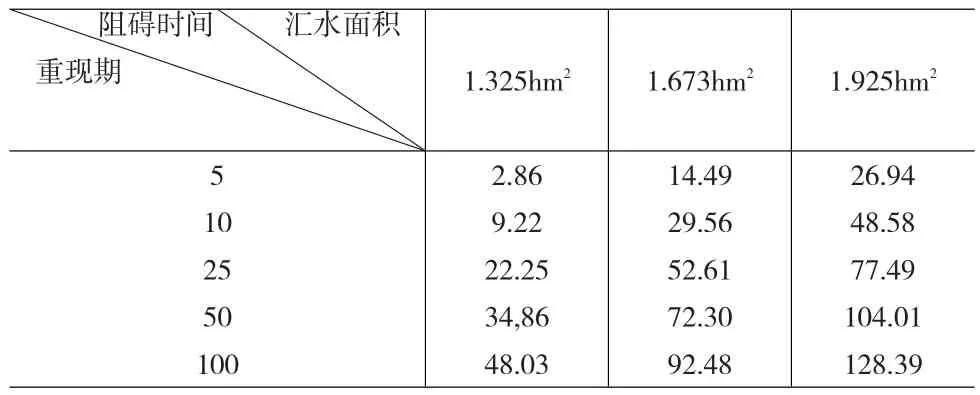
表7 固定绿化率,阻碍交通时间一览表(分钟)
3.6 模拟检验
任何模拟研究的结论都需要进行检验和确认。即检查模拟计算的逻辑正确性和确认模拟结果较准确的反映现实的真实状况。本例中计算积水深度的计算流程及公式均符合简化城市内涝模型的框架和思想。对相应的公式虽然进行了简化处理,但并不妨碍计算的准确性和可信性。
本文模拟中应用到多个变量及数据,均进行了事前的复核和验证:对北京市的暴雨强度公式,我们带入了历史数据,发现公式较好的描述了北京市的降雨状况,针对极端天气,将“北京721暴雨”数据带入公式,亦能得到近似的拟合结果;对于三组汇水面积的设定是较为保守的,实际上仅考虑加入路桥两侧辅路的面积,因此不存在夸大降雨量的可能,而又同时将高程变化的因素寓于模型分析之中;模拟分析中的排水管径和根数均符合国家相关标准;堵塞系数反映生活垃圾对管网的影响,其设定亦为保守的;绿化率的设定已经包含本例中的最小和最大值,因此已经能够充分说明问题,现实中很多立交桥下基本上是没有透水砖和绿化带的,因此模型设定较为合理。综上模型的计算逻辑和基础数据是较为准确和可靠的。在此基础上,模型模拟的积水深度和相应的受灾概率,同现实的实际状况是相符合的。
4 结论及建议
本文将城市内涝模型同蒙特卡罗模拟方法相结合,以实例的形式说明如何在内涝风险评估中综合运用相关数据和模拟方法,结论总结如下。
(1)本文的主要创新在于将蒙特卡罗方法和自助法引入到城市内涝模型的风险评估之中,将统计模拟方法同历史降雨数据相结合,得到的风险概率值是包含了评估对象所在地的历史降雨信息,因此评估的结果更有现实意义。过去暴雨强度公式应用于内涝风险评估时,都是给定具体的参数如降雨历时和重现期,但这种方法并不包含参数在历史降雨中出现的概率,因此推测的结论更偏重于理论。本文采用1000次模拟的方法,相当于在过去的降雨数据中随机选择1000场降雨在立交桥重新降落,而后评估内涝风险,因此相比而言更有现实意义。
(2)重现期的提高对于城市内涝灾害发生的概率有显著影响,因此针对极端天气,气象部门应当及时发布暴雨预警,并将灾害的等级以更加直观的形式通知公众。交警部门应当对提前对易积水的路段进行临时性的交通管制,避免灾害与悲剧的发生。
(3)模拟结果也表明排水系统设计标准落后于城市建设步伐,对于地势低洼的区域应当增设排水设备,在交通流和人流密集的区域将设计的重现期提高到50年或是100年。类似于地铁口、地下停车场、下凹式立交桥的建筑物应当进行内涝风险评估,并根据评估结果配备大型水泵等排水设施。政府应当继续推进雨污分流工作,避免强降雨时下水管网的堵塞。
(4)模拟结果也能说明在重现期较小时,提高道路两侧绿化水平可以降低内涝发生的风险。城市建设过程中,牺牲掉部分绿化带拓宽道路是很多地区采用的方法,但模拟表明这将提高内涝的风险,因此保持适度的绿化水平,采用透水砖等渗水效果较好的材料对于防范内涝是十分必要的。
(5)内涝问题是一个复杂的系统问题,评估其风险需要综合多方面的数据进行分析。内涝风险评估不仅需要地面高程数据、降水数据也需要下水管网分布、地面建筑物配套设施等诸多方面的数据。因此政府更加需要注重对各个部门分散的数据进行共享和综合利用,建立相关的主题数据仓库满足市政管理需要,在大数据时代“信息孤岛”是一种资源浪费。
[1]黄津辉.天津市设计暴雨方法比较及公式修正[J].天津大学学报,2013,(4).
[2]尹占娥.基于小尺度的城市暴雨内涝灾害情景模拟与风险评估[J].地理学报,2010,(5).
[3]肖枝洪,朱强.统计模拟及其R实现[M].武汉:武汉大学出版社,2010,(4).
[4]茆诗松,王静龙.高等数理统计[M].北京:高等教育出版社,2006,(5).
[5]David A.Freedman.统计模型理论和实践吴喜之译.[M].北京:机械工业出版社,2010.
[6]薛丰昌.基于GIS的城市内涝积水数值模拟[J].测绘与空间地理信息,2012,(12).
[7]任雨.天津地区设计暴雨强度的推算与适用[J].应用气象学报,2012,(6).
[8]李苗.面雨量在城市内涝预报中的应用试验[J].气象与环境科学,2011,34(4).
