基于汇水度的平坦地区水系提取算法研究

苏丹丹

(长春师范大学城市与环境科学学院，吉林长春 130032)

基于汇水度的平坦地区水系提取算法研究

苏丹丹

(长春师范大学城市与环境科学学院，吉林长春 130032)

本文在已有剪枝算法的基础上进行改进，以“不同地形汇聚水的能力不同”为突破点，定义“汇水度”，反映此点上游地形特征，表征此种地形汇聚水的能力；再以“汇水度”作为剪枝条件，进行水系剪枝。选取汇水能力相对较弱的平坦地区进行对比实验，结果表明：应用这种以“汇水度”作为判定条件的剪枝算法，识别河源的准确性有所提高，提取水系的整体形态、河源数、总河长、主河长及支流河长等水系参数与实际水系的对应参数也更加接近。

汇水度；水流连接树；河源数；总河长

近年来，研究人员将地形数字分析技术应用于水系及其它线性信息提取过程中。他们紧密围绕地形、主汇水线终点、汇水区面积、径流节点汇水值等方面进行研究，讨论其在水系提取、径流节点提取中的关键作用，尽最大可能提高水系及其他线性信息的提取精度[1-3]。可见，在进行水系及其它线性信息提取时，地形因素被作为需重点考虑的判定性因素。本文主要研究以“汇水度”为剪枝条件，进行水系提取。选取平坦地区进行剪枝算法的对比实验，实验结果表明：应用以“汇水度”为判定条件的剪枝算法，可以使识别河源的准确性得到明显提高，也使得提取水系的整体形态、河源数、主河长及支流河长等水系参数均与实际水系更加接近。

1 汇水度

汇水域的大小是由汇水域中的节点数确定的，流经路径长短可以由汇水域上水的最终集中点到上游的最长路径来近似表达。对于一个汇水域来说，汇水域越大且水流经过的路径越短，则其汇水能力就越强。

汇水度反映汇水域形状对汇水能力的影响程度。对于一个节点来说，如果不考虑水的流速和渗透的因素，一个节点处的汇水能力可以用周围节点中流向此节点的节点个数来确定，如果周围节点的水都流向这个节点，那么此节点处的汇水能力最强。对于一个区域来说，汇水度是表示“汇水域上的总节点数”和“汇水域上水流最长路径上节点数”之间关系的函数。因为一个汇水域中只有一个水的集中节点，所以把这个水的集中节点的汇水度看作是此汇水域的汇水度。由于所定义的汇水度与汇水域的大小无关，只与汇水域的形状有关。所以，可以设定当汇水域形状不变、汇水域无限增大且节点密度不变时，汇水度有极限值。但是，汇聚的水量却与汇水域的大小密切相关。因此，在使用汇水度时，通常要乘以一个与汇水域的大小相关的量来进行调节。

下面用两个特殊地形导出汇水度的一个定义公式。当汇水域是圆形漏斗状的区域时，汇水能力最强，其节点总数与圆的面积成正比，水流最长路径上的节点数与圆的半径成正比。当在一个斜面上，汇水域是个长条的狭窄区域时，汇水能力最弱，此汇水域上的总节点数和水流最长路径上的节点数近似相等。汇水度的定义公式如式(1)。

(1)

其中，k为待定系数，s为汇水域上的总节点数，l为汇水域上水流最长路径上的节点数。根据式(1)进行计算，当汇水域在斜面上时，s和l相等，其汇水度为0；当汇水域是圆形漏斗状的区域时，汇水度的极限值是kπ，为常数。

如果选取汇水域的形状大致为树叶状的菱形，设定菱形的两条对角线的长度比为2，集水点在长对角线的一个端点上，那么将此菱形作为标准形，其汇水度设为1，从而导出k值。推导过程如下：设菱形的短对角线长度为l，菱形的长对角线长度为l的2倍(即最长水流路径长度)，菱形面积计算公式如式(2)；当l趋向于正无穷大时，标准形的汇水度设为1，如式(3)所示，从而计算出k值为4；再将k值代入式(1)，即得汇水度计算公式。由汇水度的定义公式可知，当s和l相等时，汇水度为0，是汇水度的最小值；当汇水域形状是漏斗状且汇水域面积无限增大时，汇水度为4π，是汇水度的极限最大值。

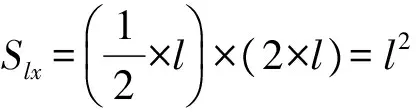
(2)

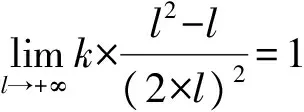
(3)

2 以汇水度为剪枝条件的水系提取算法设计

以汇水度为剪枝条件的水系提取算法，实际上就是基于随机水流模型的水系剪枝算法的改进算法。

基于随机水流模型的水系剪枝算法主要包括以下四步：第一步，在随机水流模型中计算每个网格点水的流向，连接这些点，形成多个树枝状图。第二步，使用泛滥算法(水填满较小的洼地，继续向下游流动)，把一些树枝连接到另外一些树枝上，形成较大的树枝，即水流连接树。第三步，针对水流连接树，根据剪枝条件进行剪枝，剩余树干部分即为提取的水系。第四步，把提取的水系进行光滑处理，使提取的水系显得更为自然，与实际水系更加接近。在该算法的第三步中，仅考虑“枝的大小”作为剪枝条件(如果“枝的大小”大于允许形成最小汇水盆地的分支上节点的个数，此分支保留；如果“枝的大小”小于允许存在的最小一级域的分支上节点的个数，此分支被剪除)。

以汇水度为剪枝条件的水系提取算法，不仅考虑“枝的大小”作为剪枝条件，而且还将“分枝根点的汇水度”作为另一个重要的剪枝条件，实现“基于随机水流模型的水系剪枝算法”的改进。分枝根点的汇水度反映此点上游地形特征，体现此水系分支上游汇水域地形的汇水能力的强弱程度。剪枝时设定大、小两个“汇水域”阈值，当待剪枝的汇水域小于小的阈值时，此枝被剪掉；当待剪枝的汇水域大于大的阈值时，此枝保留；当待剪枝的汇水域在这两个阈值之间时，才根据“汇水度”决定此枝的保留或剪掉。如果枝的根点的汇水度达到设定的汇水度阈值以上时，说明此水系分支所处地形的汇水能力较强，此处可以形成河流；如果枝的根点的汇水度低于设定的汇水度阈值，说明此水系分支所处地形的汇水能力不足以形成水系，此枝须被剪除。剪枝过程是由下游向上游逐个节点进行的。

3 实验与讨论

3.1 实验区域及实验数据源

实验区域地理坐标为127°26′04″E～127°32′02″E，45°43′13″N～45°51′37″N。该区域包括黑龙江省宾县宾州河及周边流域，其地势平缓，属于漫岗丘陵地貌。实验区域内实际水系的河源数为30个，总河长为186.51 km，主河长为64.24 km，支流河长为122.27 km。图1是从Google Earth中根据该实验区域内实际水系情况，进行手工绘制的水系原图。

实验数据源获取过程如下：设比例尺为1∶10000，点间距为60米，从Google Earth上提取实验区域内所有网格点的地理坐标和高程[4-5]；然后，将其投影变换；最后，设置网格线素X方向间距和Y方向间距均为5，运用“普通克里格”方法计算等高线图，并将其作为实验数据源(图2)。

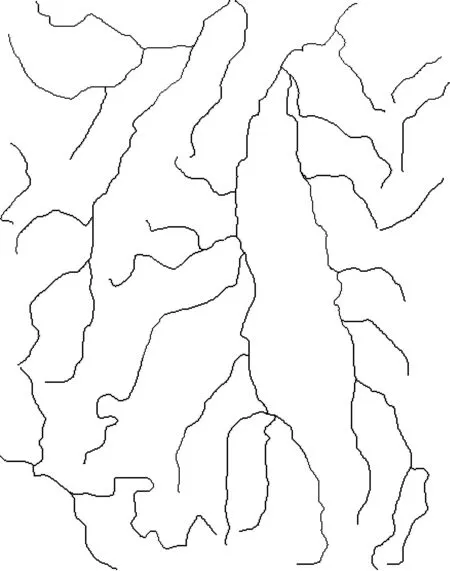
图1 实验区域内水系手绘原图

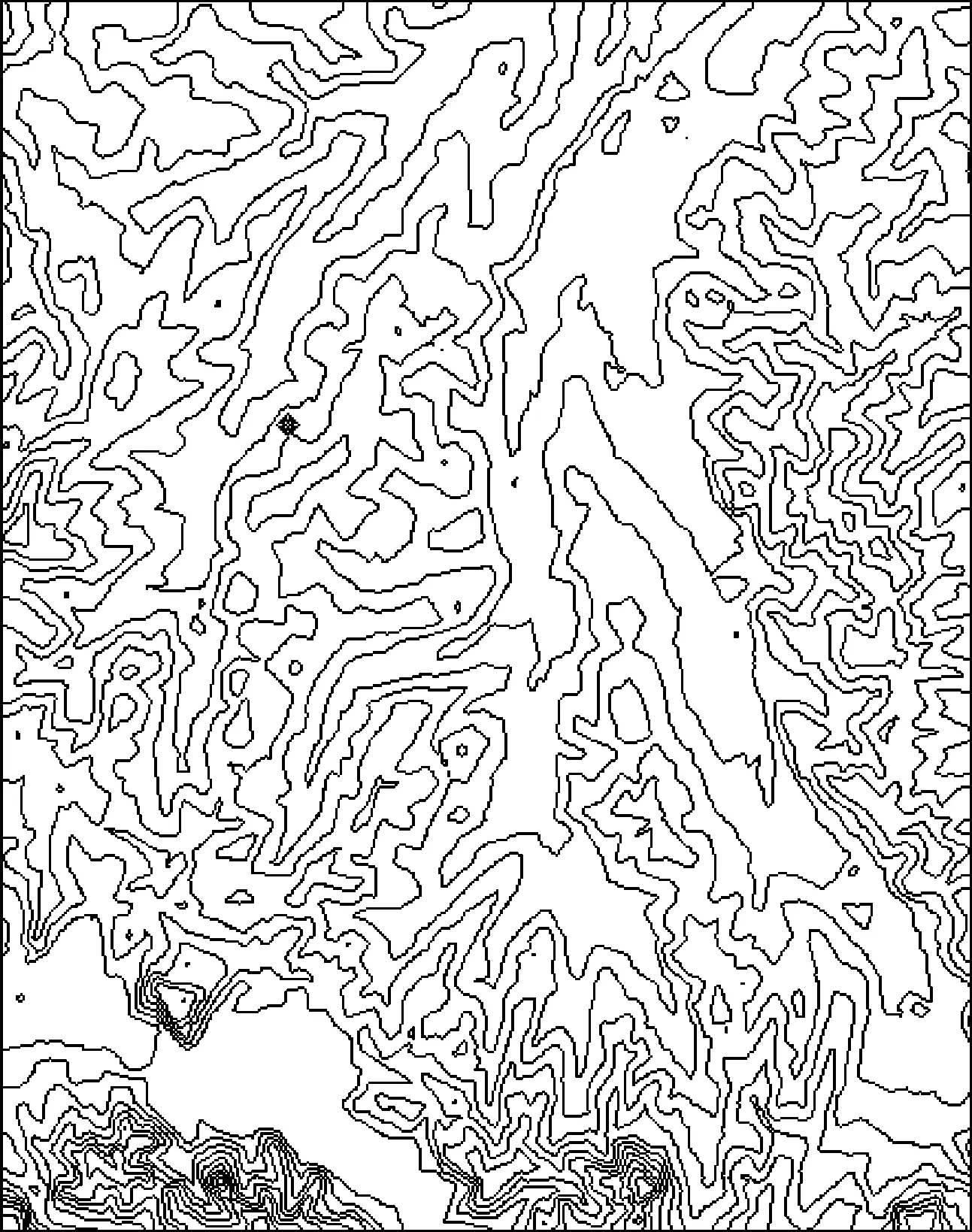
图2 实验区域等高线图

3.2 实验讨论

3.2.1 基于随机水流模型水系剪枝的实验讨论

以随机水流模型为基础，提取水系与实际水系的对应参数对比见表1。与应用ARCGIS软件提取的水系相比，基于随机水流模型提取水系的整体形态、河源数、总河长、主河长及支流河长等水系参数均更趋近于实际水系的对应参数。

表1 实际水系与应用本算法提取水系的对应参数对比

3.2.2 以汇水度为剪枝条件提取水系的实验讨论

以随机水流模型为基础，以“枝的大小”和“汇水度”作为剪枝条件，提取水系与实际水系的对应参数对比见表2。可见，充分考虑实验区域的地形特征，不仅保证提取水系的河源数与实际水系的河源数一致，还确保总河长、主河长、支流河长的相对误差均低于1%，提取精度有所提高。

表2 实际水系与应用本算法提取水系的对应参数对比

4 结论

在平坦地区，基于随机水流模型提取水系，以“枝的大小”作为剪枝条件，提取水系的整体形态、河源数、总河长、主河长及支流河长等水系参数均更趋近于实际水系的对应参数，各水系分支末端处理精确程度不够，各水系参数的相对误差均高于1%。所以，当汇水域较小时，考虑地形对汇水能力的影响，引入“汇水度”作为剪枝的另一重要条件，有效地提高河源的可靠性，提取水系的河源数和总河长的相对误差均为0，主河长和支流河长的相对误差也降至1%以内，说明提取水系与实际水系最为接近。

[1]余桂贤,孙光耀,郑凯梅，等.多级汇水盆地的自动提取[J].物探化探计算技术，2002(4):349-351.

[2]朱庆,田一翔,张叶廷.从规则格网DEM自动提取汇水区域及其子区域的方法[J].测绘学报，2005(2):129-133.

[3]张书亮,孙玉婷,曾巧玲，等.城市雨水流域汇水区自动划分[J].辽宁工程技术大学学报，2007(4):630-632.

[4]刘文荣.集成Google Earth的高程提取程序开发及在环评中的应用[J].煤炭工程，2011(5):122-124.

[5]唐胜军,张立东,王少杰.浅谈Google地球高程数据的提取[J].河南水利与南水北调，2012(8):105-106.

Research of Drainage Network Extraction Algorithm on Pruning Condition of the Cohesion-degree on Flat Area

SU Dan-dan

(College of Urban and Environmental Sciences，Changchun Normal University,Changchun Jilin 130032, China)

The existing pruning algorithm was improved, and the catchment ability of water in different terrains is known as the breakthrough point of studying. “Cohesion-degree” is defined, and it reflects the topography of the upstream and the water catchment ability in the terrain. As a pruning condition of “cohesion-degree”, the branches of water are pruned. On the flat area, the contrast experiments are conducted, and the results shows that: the recognition accuracy of the sources of river is improved, because of “the cohesion-degree” being regarded as a condition of the pruning algorithm. The parameters of the extracted river, such as the whole river, the number of the sources of river, the length of the whole river, the length of the main river, the length of the branches of the river, are more closed to the parameters of the actual river.

cohesion-degree; drainage dendrogram; number of river sources; length of whole river

2017-04-12

苏丹丹(1980- )，女，高级实验师，博士，从事地球信息科学研究。

K909

A

2095-7602(2017)08-0080-04