基于加权L1极小化模型选择线性回归模型中的自变量求解

李立亚,郑桃云

（1.湖北第二师范学院 数学与统计学院，武汉 430205；2.湖北中医药大学护理学院，武汉 430065）

1 问题的提出

在上述介绍中，我们了解了自变量选择的几个准则，以及几种自变量选择方法的基本思想。从中可以知道经典的自变量选择有局限性：自变量的所有可能子集构成了2m-1个回归方程，当可供选择的自变量不太多时，用全局择优法可以求出一切可能的回归方程，然后用几个选元准则去挑选出最优的方程，但是，当自变量的个数较多时，要求出所有可能的回归方程是非常困难的。还有就是，根据不同的方法和准则，选出的最优回归模型也不一定相同，真正哪个回归模型最优，同样面临选择的困难。逐步回归法也有明显的不足之处：前进法不能反映引进新的自变量后的变化情况，因为某个自变量开始可能是显著的，但当引入其他自变量后它就变得不显著了，但是也没有机会将其剔除，即一旦引入，就是“终身制”的；后退法同样存在类似的问题，一旦某个自变量被剔除，他就再也没有机会重新进入回归方程，而且一开始把全部自变量引入回归方程，这样计算量很大；即使是吸收了前进法和后退法的优点，克服了它们的不足的最受欢迎的逐步回归法，也有它的不完美的地方，即当自变量的个数达到几百个，甚至更多上千万个的时候，它也会慢慢失去其相对的优越性，不能成为我们理想的线性回归模型的选元方法。

本文主要采用ℓ1极小化模型在线性回归模型中自变量选择上的应用，即通过ℓ1极小化理论和数据的稀疏性的应用，从所有可能的回归系数矩阵β中选出含零元最多的一个，那么线性回归中对应零元系数的自变量便可以舍去。这样便大大的减少了自变量的个数，从而减轻了回归的计算量并且能保持回归模型的质量。

2 利用ℓ1极小化模型选择线性回归模型的自变量

2.1 普通最小二乘法的参数估计

在一个实际问题的线性回归建模中，有m个可供选择的自变量 x1，x2，…，xm，因变量为y，并对该问题进行n次观测，所得数据为(X1，X2，…Xm，y)。其线性回归模型为

其中，β0，β1，β2…βm是 m+1个未知参数，β0称为回归常数，β1，β2…βm称为回归系数，回归系数代表了每个自变量对回归模型所做贡献的大小，系数越大，贡献也越大；系数为零，没有贡献，则该自变量可以舍弃。ε是随机误差，我们假定误差项ε服从正态分布，即ε～N(0，σ2)

用矩阵表示该线性回归的一般式，令：

性回归模型为：

其中X是一个n×(m+1)阶矩阵。对该线性回归模型用普通的最小二乘法计算参数估计值，即求使观测值与回归值的离差最小下的参数：

当（X'X）-1存在时，即可得回归参数的最小二乘估计为：

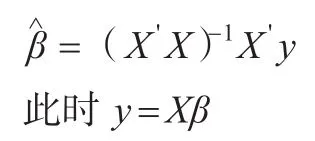
2.2 ℓ1-minmization model

最小二乘法是用所有的自变量来做线性回归，并没有起到回归选元的作用。而经典的线性回归选元方法，对自变量的个数较多时回归效果并不好。如今人们发现可以通过ℓ1极小化理论和数据的稀疏性来大大的减少自变量的个数且能保持回归模型的质量：要使线性回归模型y=β0+β1x1+…+βmxm+ε简单而高效，我们可以减少不必要的自变量来减轻计算量，由于回归系数代表了每个自变量对回归模型所做贡献的大小，系数越大，贡献也越大；系数为零，没有贡献，则该自变量可以舍弃。那么只要使自变量对应的回归系数估计值βi尽可能为零就可以达到此目的，即使参数估计值尽可能的稀疏。由ℓ1极小化理论中信号的稀疏表示原理可知，即求

又因为ℓ1最小范数在一定条件下和ℓ0最小范数具有等价性，可得到相同的解。而且相较ℓ0最小范数，ℓ1最小范数更具有优势，它便于计算。由于ℓ0最小范数是要求向量元素不为零的最小个数，它是一个NP难题，要求这个问题是很难的。而ℓ1最小范数是要求向量元素之和的最小值，它将非凸化问题转化为凸化问题来求最优化求解，即将求ℓ0范数的NP难题转变为求ℓ1范数的线性问题来找到信号的逼近，针对极小化ℓ1范数模型来提出线性规划方法，这个问题的求解方法有很多，更便于计算。所以可以替换（2）如下：

2.3 加权ℓ1-minmization model

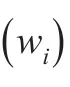
（4）当收敛或ℓ达到指定的最大迭代次数ℓmax时终止程序。否则，增加ℓ并回到第2步骤。

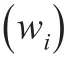
2.4 加权ℓ1极小化模型选择线性回归模型的自变量

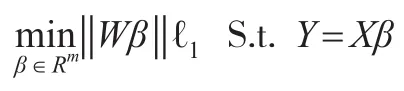
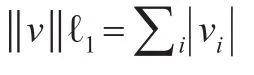
接下来将式子(6)转变为一个二次规划形式，它是通过将所求变量β分为两部分完成的，通常称这两部分为积极和消极的部分，设：

2.5 GPSR(稀疏重建的梯度投影)法求解二次规划问题

（4）当执行到给定的最大次数或有满足的近似解

3 结果

3.1 仿真数据结果

用仿真方法来证实：加权ℓ1极小化模型能有效地选择线性回归模型中的自变量。仿真数据从如下线性回归模型产生：

在上述回归模型中，所含参数的个数为100个，第2，3，5，7，9个参数不为0，其它参数均为0；残差项服从均值为0，标准差为0.1的正态分布。假设自变量均是0-1之间的均匀分布的随机数。利用Matlab自带函数生产随机数的方法，产生50组样本值及每组样本值相应的残差项，根据上述回归模型，可计算相应因变量的值。因变量的值如图1所表示。

由这50组样本数据和相应的因变量的值，需要估计回归分析模型中参数的值。明显的，利用普通的线性回归模型中的最小二乘法，因这些数据只能构造50个线性方程，无法准确的估计真实的参数。然而，利用加权ℓ1极小化模型，可以几乎完美的估计出真实的参数。如图二所表示。原因在于加权ℓ1极小化模型，它除了利用数据提供的信息之外，还能有效的利用待估参数先验信息，即稀疏性。而普通的线性回归模型中的最小二乘法只能利用数据提供的信息。

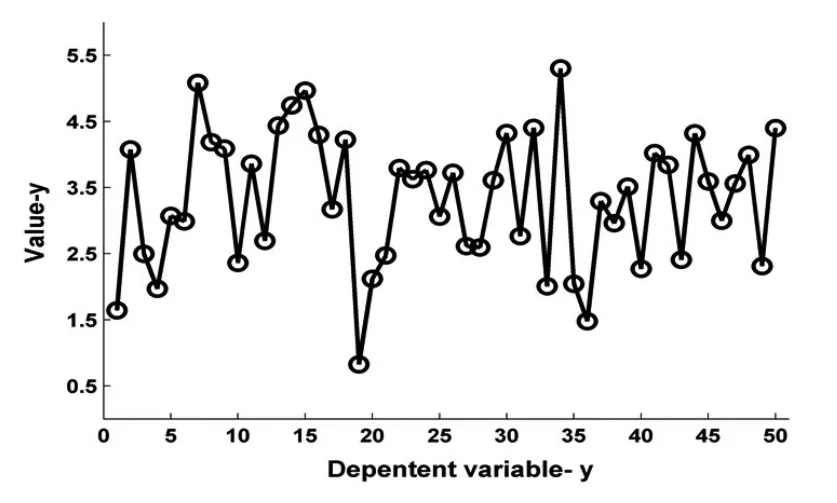
图1 为仿真产生的50组样本值所对应的因变量的值

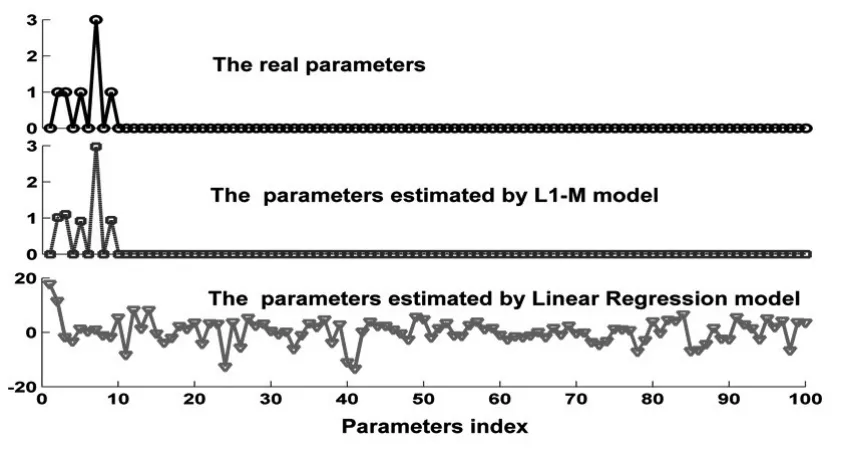
图2 L1极小化模型对线性回归系数的有效性

该仿真模型结论表明：利用加权ℓ1极小化方法求得的回归系数估计值的非零个数，远远小于最小二乘法求出的个数，且它极为接近原先设定的较为稀疏的实际系数值，几乎可以完全模拟出实际的自变量系数。由于回归系数为零的自变量对因变量没有任何贡献，可以剔除，所以，该方法可以大大的减少自变量的个数，起到线性回归选元的作用。

3.2 实验数据结果

本文选取2009年《中国统计年鉴》我国30个省、市、自治区（西藏地区失业率数据缺失，因此从样本中剔除西藏）2008年的数据。

现实生活中，影响一个地区居民消费的因素有很多，例如，一个地区的人均生产总值、收入水平、消费价格指数、生活必需品的花费等。本例选取9个解释变量研究城镇居民家庭平均每人全年的消费性支出y，解释变量为：x1居民的食品花费，x2居民的服装花费，x3居民的居住花费，x4居民的医疗花费，x5居民的教育花费，x6地区的职工平均工资，x7地区的人均GDP，x8地区的消费价格指数，x9地区的失业率。本例题以居民的消费性支出（元）为因变量，以如上9个变量为自变量，其中，自变量x1，x2单位为元，x9单位为%。文中利用加权ℓ1极小化模型来这些对自变量作变量选择，并用Matlab编写程序。

β=[1.2083-0.5232，0-0，0.5550-0.3883，0-0，0-0，0.7376-0.5023，0.5147-0.3591，0-0，0-0]=[0.6851，0，0.1667，0，0，0.2353，0.1556，0，0]

其中，第2、4、5、8、9个回归系数元素为零，则其对应的自变量对因变量没有任何影响，即可以剔除x2、x4、x5、x8、x9。所以，剩下的自变量 x1、x3、x6、x7为程序挑选的自变量，可建立最优的线性回归模型。即居民的食品花费，居民的居住花费，地区的职工平均工资，地区的人均GDP是建立线性回归方程的最优自变量，对所求因变量居民的消费性支出起到显著的影响。

该结果与实际是非常相符合的。我们知道现今社会，大部分人们的消费支出都用在了衣食住行上，但并不是它们都很重要，因为人可以不赶潮流，不买新衣服，但却不能不吃饭，不租房睡觉，所以，居民的食品花费（x1）和居民的居住花费（x3），对居民的消费性支出有很大的影响，而居民的服装花费（x2）不及它们的影响程度。同时，只要人们好好对待自己的身体，养成良好的作息习惯，就可以避免大量的医疗花费；而且由于地方省市的经济大不相同，有的地方人们生活水平高，可以享受良好的教育环境，而有的地方人们食不果腹，接受教育无从谈起，所以，居民的医疗花费（x4）和居民的教育花费（x5），对居民的消费性支出并没有很大的影响。有工资就有钱来消费，人均GDP高的地方人们的生活水平就高一些，人们大多有钱用来消费，所以，地区的职工平均工资（x6）和地区的人均GDP（x7），是显著的影响因素。而（x8）地区的消费价格指数和（x9）地区的失业率对不同的地区不尽相同，并不能成为显著的影响因素。综述所述，挑选居民的食品花费，居民的居住花费，地区的职工平均工资，地区的人均GDP为建立线性回归方程的最优自变量，是非常符合实际情况的。另外，我们比较了最小二乘法与加权ℓ1极小化方法所得到的参数估计值，见下表。

表1 最小二乘与加权ℓ1极小化模型得到的待估参数

可以看出利用加权极小化模型所得到的回归系数估计值更为简单，且更合理。表一中最小二乘法得到的回归系数值都不为零，不能舍去任何自变量，并没有起到线性回归选元的作用，而且这些回归系数并不是能很好的解释因变量的变化。因为消费性支出是指用于家庭日常生活的全部支出，包括食品、衣着、居住、家庭设备用品及服务、医疗保建、交通和通信、娱乐教育文化服务、其他商品和服务八大类等，所以将居民的医疗花费（x4）和居民的教育花费（x5）的回归系数定义为负数是不合理的。反观加权极小化模型，它求得的回归系数值更为稀疏，可以舍弃许多不必要的自变量，减少计算量，极为有效的挑选出显著的影响因素，得到最优线性回归方程。

[1]何晓群，刘文卿.应用回归分析（第二版）.北京：中国人民大学出版社，2011.

[2]石光明.刘丹华.高大化.刘哲.林杰.王良君压缩感知理论及其研究进展-ACTA Electronica Sinica 2009，37(5).

[3]Donoho D.Tsaig Y Extensions of Compressed Sensing[J].Signal Processing,2006，(3).

[4]Candes E J,Wakin M B,Boyd S P.Enhancing Sparsity by Reweightedℓ1Minimization[J].Journal of Fowrier Ana Lysis and Applications,2008,14(5).