网络购物小数定律在大数据和EWA学习模型下的修正

龚谊承，徐一娉

（武汉科技大学a.理学院；b.冶金工业过程系统科学湖北省重点实验室，武汉430065）

0 引言

随着网络的发展，数据流集合的规模已从GB到PB甚至以ZB(1021)等单位来计数。学者们敏锐地注意到其规模性、即时性、非线性性和可获得性符合大数据的特征，并开始利用大数据展开对网络经济的探讨。但是，探讨如何利用大数据减少消费者可能受到虚假评价误导而犯下小数定律错误的文献尚有待发展。本文以网络大数据的出现为契机，将网络用户评价视为带噪音的大数据，将网购视为消费者和商家的一种群体博弈，利用EWA学习模型分析消费者在浏览带噪评价数据时从小数定律向大数定律对应的理性策略修正的过程。以期减少消费者网上购物的风险，或有助于政府充分利用网络经济大数据成立市场监管机构，引导消费者远离“小数定律”陷阱而靠近理性决策有利于大数据时代网络经济市场的更好运行。

1 用户评价误导网络消费者的小数定律视角

小数定律[1]是Amos Tversky和Daniel Kahneman总结出来的一种行为经济学规律，用以说明人们在面临不确定环境时，往往会违背基本的大数定律而不由自主地滥用“典型事件”导致忘记“基本概率”。在网络购物行为中，消费者面临产品质量、卖家信誉等诸多不确定因素，此时他们浏览到的一些典型用户评价可能给他们深刻印象，进而使他们忘记正确评价卖家的信誉和产品的质量需要大量的评价数据才能得到稳定的均值，于是他们很可能受到这些典型评价数据的误导而犯下“小数定律”的错误。具体地讲，本文注意到评价数据量过小或者评价数据被筛选过是当今的网购环境下诱发“小数定律”错误的两大因素。

1.1 数据量过小容易导致网购中的小数定律错误

大数定律强调样本的数目要尽可能大，这样其样本均值就会收敛于真实的期望。事实上，样本数目过小会导致样本平均值更加不稳定。

在网购前,消费者经常难以确定网上商品的质量与如商家所描述的那么好，此时购物评价对消费者的决策起到了重要的作用。笔者对某款手机在淘宝网上选取红心、蓝钻、蓝冠和皇冠四个等级各10家网店来收集数据，其中淘宝网商家由红心到皇冠的信用等级是由低到高的。信用评价由每一次交易成功后的买家作出，按照5颗星为好评满分值，0颗星为最差评，超过3颗星的评价视为好评，其基本的统计结果见表1。

从表1可见：信用等级高的商家，其成交量基本上会更高。但并非信用等级高的商家获得的好评率就更有优势：比如蓝钻网店评价一个月的均值为4.8，而蓝冠的仅为4.75。可见，消费者依据寥寥数百条评价所呈现的高达97%以上的好评率而相信商品本身具有与评分相符的品质，进而做出的购买决策可能已掉入小数定律错误中。因为在历史成交量小的商铺中，其评价数据是小样本，但消费者错误地运用了大数定律的结论：商品的历史性评价代表了商品的实际品质的平均水平。由此可见当网购质量不确定时,消费者容易将从大样本中的结论错误地移植到小样本中的原因是：受到了自身所能了解的评价数据之数目的限制。

表1 淘宝网四种信用类型商家所获评价的统计结果

1.2 被筛选的数据容易导致小数定律错误的产生

为避免小数定律误区，网购消费者做决策前一般会尽可能多地搜寻相关评价信息。但如果这些大量的评价信息是被筛选过的，他依然会被误导而陷入小数定律的错误、偏离理性。

这个道理可以通过一位股票投资者的经历来说明。假设通过亲身经历，该股票投资者发现一位基金经理在过去两年中的投资业绩好于平均情况，于是他就倾向于得出这位经理要比一般经理优秀的结论。然而事实可能是：他所搜集的亲身经历的数据是他人精心筛选的，其实与基金经理的水平无关。情况可能是这样的：基金经理选定某支股票，第一周发10000条短信预言其涨跌，其中5000条说该股票涨另外5000条说跌；第二周向其中说对的5000人再发一短信，其中2500条说该股票涨而另2500条说该股票跌；第三周他再向说对的2500人发短信，其中1250条说该股票会涨，另1250条说该股票会跌。最后有1250人会发现这位股神大哥连续3次说对该股票的涨跌，于是会得出这位经理对该股票的涨跌预测是要比一般经理优秀的结论。然而仔细回顾这起事例会发现：他得出的结论其实与该经理的预测股票价格涨跌的真实能力无关，根本原因是其所观测到数据是被精心筛选之后呈现出来的。

类似地，网购的消费者如果参考的消费者评价数据也是经过商家以某种手段筛选而来的，那么即使样本数据的规模够大，其得到的关于商品质量的结论依然可能是受到误导的。

2 基于网络评价大数据的小数定律修正思路

评价数据可能导致的小数定律成为影响网购进一步发展的阻力，因此改善这种经济误区的途径令人期待。笔者尝试将客观上快速发展的网络大数据与主观上调整博弈策略的EWA学习模型相结合，以期为消费者避开小数定律提供一种参考途径。

2.1 大数据使可获得的评价数据的样本量和可信度同时提升

关于大数据的热烈讨论由此在学术界和商业界备受关注。虽然目前还没有一个明确的关于大数据的定义，但是对于大数据的特征描述已经有了一些共识，笔者采用周涛（2013）所描述的四个特点[2]：其一，数据规模巨大且持续保持高速增长；其二，数据价值的增长与规模的增长正相关；其三，数据能充分发挥其外部性并通过与某些相关数据交叉融合产生远大于简单加和的巨大价值；其四，一般研究人员和开发人员可以自如获取数据的逻辑片段并进行分析处理。

从单个消费者的角度看，由于网络消费者最初掌握的数据一般比较少，而且他们一般是单次与某个商家进行交易，所以基本属于小样本认识。但是他们可以通过其他人的交易经历来能获得更多的评价数据，以摆脱典型事件的影响。随着网络竞争的发展，网络评价数据不再是某几个大型数据门户网站的专利，一般的用户不仅是数据的生产者也同时可以称为数据的利用者，比如CNNIC就提供了一种免费获得网络经济大数据的途径。因此，网络大数据使得消费者可以获得的评价数据的样本量极大地提升了。注意到在大数据时代，我们面对的数据样本就是过去资料的总和，样本就是总体，所以需要合适的数据分析技术[3]。为了充分挖掘出评价大数据的价值，笔者以为可以采用交叉验证的思想，将线上评价数据集作为基础数据集按照一定的比例来细分为训练集和测试集，将线下评价数据集作为验证数据集，实行线上与线下评价数据的交叉验证。由于线下评价基本来源于消费者3度以内的真实的社会网络，其评价的可信度比较高，所以线上与线下评价数据的交叉验证有助于提高网络评价数据的可信度，从而有利于消费者对商品质量做出更正确的判断。

然而，在网络大数据可以获得的前提下，消费者利用其来规避小数定律误区的过程中仍有两个问题需要解决：其一，对卖家宣称的同等质量价格最低这类消息，消费者应该最少浏览多少相应的评价信息才能保证其作出的决策已经走出小数定律误区？其二，消费者从非理性决策到理性决策的演化过程如何？本文拟从博弈论的角度构建网络经济系统中经济主体之间的网络演化博弈模型，得到其演化均衡路径。

2.2 消费者评价导致的小数定律的演化博弈分析视角

网购过程中，某个特定的消费者购买某个特定商家产品的行为可以视为一次合作博弈。

消费者考虑的是商品的质量、价格、物流速度以及商品对自己效用的大小；而商家考虑的则是成本和收益。网购成功意味着合作博弈形成了合作，其对应价格下各自的收益就是一种双方认可的分配方案。因此，消费者和某商家之间的一次交易本质上是一次合作博弈。

考虑初始状态下某消费者与商家之间的一次网购博弈。假设消费者有三种可能的策略，而商家有四种可能的策略，见表2。假设该商家当前拥有的评价数据有n条，其中好评m条，意向交易价格为p，商家刷信用的成本为c1，提供货真价实商品的成本为c2，提供假劣商品的成本为c3(c3＜c2)。类似地，假设消费者享用货真价实商品的主观效用为u2，享受假劣商品的效用为u3(u3＜u2)。设消费评价对消费者主观感受的积极影响系数为u1(0＜u1＜1)，当消费者不相信评价而选择不购买该商品时，其感受半信半疑中挽救了1-u1补偿系数的一大半，假设为九成。一次静态博弈模型如表2所示，在此理论上可计算其Nash均衡策略和收益结果。

表2 初期代表性消费者与商家的一次评价接触博弈

2.3 EWA算法的基本思想和原理

由于对商品质量的不确定，每次博弈前消费者会参考前期消费者的评价信息来调整本次的策略，所以一次网购博弈是建立在局中人对网购群体历史博弈结果的学习和观察基础上的，因此一次网购博弈本质上是群体博弈演化过程中的某个状态。消费者和商家都会通过学习来改善自己的策略，从而达到演化均衡，其学习的效果依赖于具体的策略学习机理。

目前常用到的演化决策机制有四种[4]：最优反应动态机制、复制动态决策机制，基于随机过程或群智能优化算法的决策机制，以及基于神经网络或强化学习[5]的决策机制。其中，强化学习模型是最常用的两种动态决策机制之一，它使成功的策略被加强，但没有考虑未选择策略的收益信息和对手的可能信念。信念学习模型[6]试图使博弈参与者根据其他参与者先前行动的历史事件形成对别人会如何行动的信念，根据这些信念计算各种策略的期望收益，并以较高的频率选择能获得较高期望支付的策略，但没有考虑到过去选择成功策略对后来选择的影响。本文采用1999年由Camerer和Chong提出的经验权重魅力值EWA（experience-weighted attraction）学习算法[7]，该学习机理综合了强化学习和信念学习的优点，能更好地融合大数据评价信息，同时考虑成功策略的积极评价和不成功策略的消极评价的信念调整，比强化学习和信念学习有更好的解释能力。

EWA学习模型的基本模型如公式（1）、（2）和（3）所示的模型。

3 模拟算例分析

3.1 基于大数据和EWA学习的仿真流程

结合能掌握的评价信息，可以按照如下7个步骤来展开EWA的网上购物仿真。

步骤1：依据当前掌握的历史交易评价信息，估算表2所示的博弈模型中的个参数取值，并将各种策略的初始魅力值理解为表2中的收益值，即商家利润或消费者的效用大小；

步骤2：根据每一个策略的初始魅力值，利用（3）式计算其选择概率；

步骤3：利用Matlab产生一个(0,1)之间的随机数，根据该随机数，选择卖家和买家的策略；

步骤4：根据网上购物供需关系进行出清；

步骤5：卖家与买家根据出清结果计算其利润；

步骤6：按照式（1）修改策略集合中各个策略的魅力值；

步骤7：若还没有达到结束的条件，则返回步骤1，结合即时产生的评价数据，更新表2中的参数一收益值，开始下一轮学习，当达到终止条件时结束，或者当样本数据用尽时结束。

3.2 消费者与商家的静态评价博弈案例的Nash均衡及EWA演化

选择某款手机的销售为研究案例，将笔者手动搜集的某一品牌手机三个月累计的四个信用等级商铺的评价数据视为小数据样本。由表1可得到四个等级的商家对应于博弈模型表2中的评价总数n和好评总数m。由于评价对消费者的积极影响与其好评率成正相关，但是好评数太低时的积极影响可以忽略，所以为简单起见假设积极影响系数为u1=Max{m/n-1/2,0}。所有店铺的手机交易价格均为p=1320元，假设消费者对正品手机和假劣产品的效用分别货币化为u2=2000和u3=320元。商家提供正品和假劣产品的成本分别为c2=1000元和c3=500元，刷信用的成本c1=min{0.5m,100}.分别算出四种类型商家与消费者的参数列于表3。

表3 四种类型消费者与商家的一次评价博弈的参数值及Nash均衡策略

由表3可以得四种类型商家与消费者对应于表2所示博弈模型的收益值，可以发现前种类型的博弈中均不存在占优均衡策略。但是皇冠类型的商家，其占优策略均衡是不刷信用且货真价实地供货，然而其消费者却依然不存在占优策略均衡。

3.3 基于大数据和EWA学习的仿真结果

考虑到网购消费者对过去经验学习的能力比较强，我们设式(2)中的魅力值增长系数ρ为0.6，但是考虑到魅力值的敏感度不太高，设式(3)中的魅力值反应敏感度λ为0.4。然后，按照上述七个步骤逐步更新每一个策略的魅力值，计算其选择概率。结束的条件为魅力的代际更新值差别不超过0.05。

首先直接利用小样本集进行EWA学习的仿真结果。以R软件模拟该案例的EWA更新博弈结果，发现红心、蓝钻和蓝冠类型的商家与消费者的评价博弈的演化情形如图1所示，蓝冠类型的商家与消费者的评价博弈如图2所示，其结果一直没有稳定的趋势。而皇冠类型的商家与消费者的评价博弈的演化情形如图3所示，当评价数据更新至5千次时，其选择策略基本稳定。生产者选择不刷信用的比例约为65%，消费者选择相信评价并做出理性决策的稳定比例约为52%。

图1 红心与蓝钻商家与消费者的评价博弈策略演化

图2 蓝冠商家与消费者的评价博弈策略演化

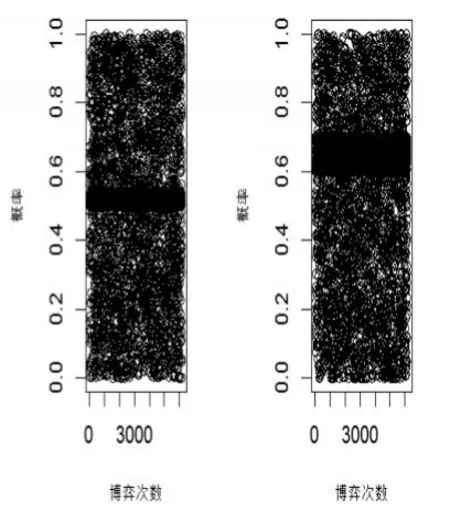
图3 皇冠商家与消费者的评价博弈策略演化

将网络可抓取的即时更新的数据视为大数据，2014年3月24日到3月30日，淘宝网的总访问次数达到了597824.2万次。当前CNNIC尚未开通购物评价统计，其中某时间段提供某款手机的商家达到529家。利用该评价数据，以R软件模拟该案例的EWA博弈策略的演化，结果表明：蓝冠类型的商家与消费者的评价博弈的演化情形如图4所示，在数据更新至约7千次时，其选择策略基本处于稳定值：生产者选择不刷信用的比例约为69%，消费者选择相信评价并做出理性决策的稳定比例约为76%。而且皇冠类型的商家和消费者的依然处于稳定如图4所示：生产者选择不刷信用的比例约为84%，消费者选择相信评价并做出理性决策的稳定比例约为81%。

图4 大数据下蓝冠商家与消费者的评价博弈策略演化

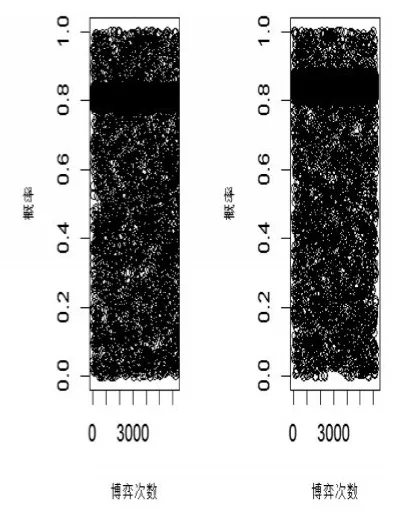
图5 大数据下皇冠商家与消费者的评价博弈策略演化

4 结论

本文利用大数据规模巨大的优势、结合消费者在浏览带噪音的评级信息时对于商品质量的学习行为，从博弈策略进化学习的角度讨论了消费者避开小数定律误区的途径。模拟结果显示：大数据使得蓝冠类型的商家与消费者的评价演化博弈由不稳定转化为稳定，其临界博弈次数约为7千次；而对于皇冠类型的商家与消费者的评价博弈，大数据下的EWA演化可以提高其良性发展的网购环境，其中生产者选择不刷信用的比例由约65%提升为约84%，表征着商家评价的真实性提高了约19%；而消费者相信评价的稳定比例由约52%提升为约81%，表征着消费者信任商家的提高了约29%。

然而，大数据来源的多样性和异构性的优势在本文中没有得到充分发挥。如果能充分量化评价中的文本、语音和图像，就能够从多维度交叉展示产品特征，评价的真实性将进一步大幅度得到提高，消费者因为评价信息不真实而误入小数定律陷阱的可能将一步减少。为了使网购环境的进一步优化，笔者期待着再此方面的进一步深入探讨的出现。

[1]K.Busche,P.Kennedy.On Economists'Belief in the Law of Small Numbers[J].Economic Inquiry,1984,22(4).

[2]周涛.什么是大数据[EB/OL].http://blog.sciencenet.cn，2012-08-18

[3]朱建平,章贵军,刘晓葳等.大数据时代下数据分析理念的辨析[J].统计研究,2014,31(2).

[4]龚谊承，王先甲，李寿贵.校企实习联盟模式变迁的进化博弈模型与演化路径[J].系统工程理论与实践，2012，32（93）.

[5]Roth,A E Erev,I.Learning in Extensive-form Games:Experimental Data and Simple Dynamic Models in the Intermediate Term[J].Games and Economic Behavior,1995,8.

[6]Crawford V.P.Adaptive Dynamicsin Coordination Games[J].Econometrica,1995,63.

[7]Camerer C F.Ho T H.Experience-Weighted Attraction Learning in Normal-form Games[J].Econometrica,1999,67.