基于线性混合模型的风险相依信度模型构建

李政宵，谢远涛，蒋 涛

(1.中国人民大学统计学院,北京100872；2.对外经济贸易大学a.保险学院b.金融学院，北京100029)

0 引言

在许多团体保险业务中，保单之间通常具有很强的相关性，使得传统信度模型在定价过程中会出现一定的偏差。同时传统的信度模型运用非参数估计的方法估计结构参数，使得在实际运用中误差偏大。Frees（1999,2001）[1]认为基于纵向数据在线性混合模型下的随机效应的最佳线性无偏预测（BLUP）[2]可以分解出信度因子，并将B-S信度，Jewell分层信度[3]和Hachemeister回归信度作为混合模型的特例进行实证研究[4]。至此，线性混合模型逐渐代替信度模型成为广泛使用的经验费率厘定的工具。

本文从传统统计的思路出发，扩展了Frees（1999，2001）的研究，认为随机效应和残差间的相关性不再局限于特殊的形式。通过引入四种不同的协方差矩阵，解释纵向数据之中存在的四种不同的相关结构。本文发现，数据间的相关结构会影响信度保费预测值的表达式。虽然信度预测值不再以线性形式表出，但是仍然能从理论上分解出信度因子，并满足信度因子的特性。最后本文运用Hachemeister(1975)的纵向数据，探究不同形式协方差矩阵下随机效应和固定效应的估计值以及信度因子的“收缩效应”，分析了数据间相关性对信度表达式的影响，为信度模型扩展提供相应的理论依据。

1 线性混合模型

在非寿险精算中经验费率厘定中，信度定价基本的思想是在经验数据和整体保单组合信息的基础上，预测个体的未来赔款额度。而线性混合模型可以用来对纵向数据建模并预测，固定效应包含了个体历史经验信息，随机效应则用来描述同一风险类别下保单的异质性（隐藏的风险特征）。因此，本文可以将线性混合模型和信度理论结合起来一起研究。

线性混合模型表示如下：

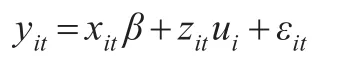
其中yit表示第i个个体在时间t的数据，i=1，2，...，n ，t=1，2，...，T（假设每个体都包含T 个观察值），xit为固定效应解释变量，zit为随机效应解释变量

矩阵形式表示如下：

y=Xβ+Zu+ε

其中残差和随机效应满足下述假定：

（1）E(εi)=0 Var(εi)=Ri

（2）ui为随机变量，期望与方差表示为 E(ui)=0,Var(ui)=Di

（3）残差与随机效应独立，即 Cov(εi，ui)=0

响应变量y的协方差矩阵由两部分构成：残差的协方差矩阵R以及随机效应的协方差矩阵ZDZ'。固定效应值影响y的期望值，随机效应只影响y的方差，衡量了数据间的离散程度。在信度理论中，固定效应可以解释为索赔平均值，信度预测值在均值的基础上通过随机效应进行调整。为了研究方便，本文假设 y的方差为：Var(y)=V=ZDZ'+R。因此响应变量 y服从期望为Xβ，方差为V 的多元分布，即 y～(Xβ，V)。

2 风险相依的信度模型

2.1 信度模型预期保费

保险数据的形式通常以纵向数据为主。下面根据线性混合模型的基本假定，建立纵向数据模型。数据结构为平衡数据结构（Balanced data），即每个单位个体有相同的观察值，将个体记为 i（i=1，2，...，n），观察值个数记为 j（T=1，2，...，T）。

第i个单位观察值矩阵记为：

2.2 风险相依的信度模型

2.2.1 风险个体i之间独立不相关

此时，随机效应相关系数满足ρu=0。y的方差矩阵简化为

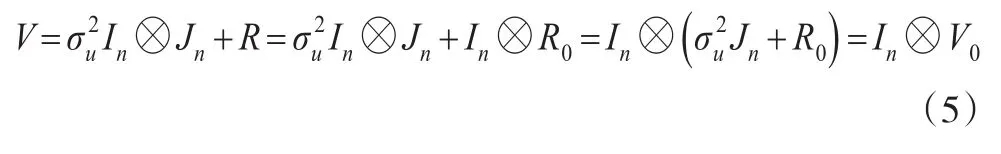
2.2.2 个体间独立不相关，并且单位个体在不同时间上的观察值也不相关。

此时满足随机效应之间的相关系数ρu=0，残差的协方差矩阵满足：

2.2.3 个体之间独立不相关，即ρu=0。但是特定的风险个体在不同时间上的观察值存在相关性。

残差的协方差矩阵表示为

综上所述，本文考虑了以上四种数据间的相关性情况，认为如果个体间和个体历史观察值之间都分别不相关，用线性混合模型得到的预测值可以分解为标准的Bühlmann信度公式,见表1。历史观察值之间的相关性会导致随机效应的方差减小；相关性越高，个体之间的风险同质性越强，赋予其他个体间信息的权重越高；反之，相关性越低，个体之间风险异质性越强，赋予个体历史经验数据的信息的权重越高。另外，不同个体之间的相关性也会影响信度预测值的表达值。虽然信度预测值不能分离出信度因子的表达式，但预测值仍然可以看作个体历史数据信息和组合信息根据权重进行调整，该权重从广义上仍然可以解释为信度因子。

2.3 特例B-S信度公式

本文探讨了数据在组间和组内都不相关的假设下，估计结果可以由Bühlmann信度公式完全表示出。下面，沿着协方差矩阵形式（2）：个体间独立不相关，不同观察值间残差也不相关，将索赔频率作为残差协方差的权重引入线性混合模型模型中，残差协方差矩阵形式调整为：

B-S信度公式不同于传统Bühlmann信度公式在于：引入索赔频率作为残差协方差矩阵的权重后，信度因子不再是单一的值，而是随着个体i的不同而不同，即满足不同个体i都存在一个信度因子zi，对该个体的经验数据和分类费率进行调整。

2.4 实证分析

数据集包含美国6个州、12个月的汽车索赔强度和索赔次数的纵向数据。在线性混合模型的框架下，将每个州视为一个单位个体i，每个个体的观察值T=12。本文选择特例的B-S信度公式作为模型，引入索赔频率对残差协方差矩阵调整。

运用SAS统计软件进行参数和方差估计，利用SAS中协方差矩阵（UN）的设定，在受限极大似然估计（REML）的估计方法下，得到固定效应的估计值（BLUE）和随机效应的预测值（BLUP）（见表2）。

Frees（2001）指出通常情况下，信度因子具有“收缩效应”：个体经验信息在信度预测值计算中起决定性作用，整体信息只是通过很小的权重进行调整，使得整体信息的定价作用收缩。根据实证结果，本文将得到的实际信度预测值与个体经验信息（完全信度预测值）相比较，信度因子基本达到90%以上，即认为实际信度值与完全信度值存在较小差异。信度因子的“收缩效应”（shrinkage effect）见图1。

表1 风险相依的信度模型

表2 估计值和信度因子

3 结论

图1 信度因子收缩效应

Frees（1997）通过线性混合模型模型推导出了4种著名的信度公式：Bühlmann信度，B-S信度，Hachemeister回归信度和Jewell分层信度。但是其研究结果都是基于个体组间和组内相互独立且不相关的假设。本文的创新点在于引入了4种协方差矩阵的形式建立组间和组内观察值的相关性，探讨了信度因子的不同表达形式，验证了B-S信度下的线性混合模型模型分解出的信度因子的收缩特性。本文发现个体间的相关性会影响信度因子的表达式形式，即如果相互独立，信度因子可以分离出与Bühlmann信度相似的表达式；反之，相关系数会对信度因子表达式进行调整，但仍然满足信度因子的根本性质。另外一方面，残差在个体观察值之间的相关性会增加个体风险同质性的假设，使得信度因子减小，而从将更多的权重赋予其他个体的信息。

以上研究都是基于线性混合模型，由于考虑数据之间的非线性关系以及存在的右尾情况，将线性混合模型扩展到广义线性混合模型（GLMMs）并尝试分解出信度因子中是今后的研究方向。沿着随机效应和残差协方差矩阵的思路，通常认为引入copula回归的结果比普通回归的结果误差更小，今后可以考虑用copula来研究个体间的相关性和个体观察值之间的相关性，并构建相应的信度模型。

[1]Edward W.Frees,Virginia,Yu Luo.A Longitudinal Data Analysis Interpretation of Credibility Models[J].Insurance:Mathematics and Economics,1999,24(3).

[2]G.K.Robinson.That BLUP is a Good Thing:The Estimation of Random of effects,with Discussion[J].Statistical Science,1991,6(1).

[3]Jewell,W.S..The use of collateral data in credibility theory:a hierarchical model[J].Giornale dell'Instituto Italiano degli Attuari,1975,（38）.

[4]Edward W.Frees,Virginia,Yu Luo,Case studies using panel data models[J].North American Actuarial Journal,2001,5(4).