淤泥质海岸波生沿岸流特性研究
2015-02-18张玮许才广钱伟
张玮,许才广,钱伟
(1.河海大学港口海岸与近海工程学院,江苏 南京 210098;2.江苏省交通科学研究院股份有限公司,江苏 南京 210017)
淤泥质海岸波生沿岸流特性研究
张玮1,许才广1,钱伟2
(1.河海大学港口海岸与近海工程学院,江苏南京210098;2.江苏省交通科学研究院股份有限公司,江苏南京210017)
摘要:淤泥质海岸波生流数值模拟缺乏有效验证数据和手段。为此,提出一种模型相互比对的验证方法,基于两种模型平台,引入三维波生流理论,经验证后开展地形坡度及波浪要素对于波生沿岸流的影响研究。研究结果表明:所建议的模型相互比对验证方法,可以有效弥补淤泥质海岸波生流实测资料匮乏的不足;淤泥质海岸波生沿岸流流速相对较小,但仍可达到潮流量级。随着岸滩坡度趋缓,波生流范围逐渐扩展,沿岸流流速相应变小;随着入射波高的增加,波生沿岸流的强度和影响范围逐渐增大;当波浪入射角度为45°时,波生沿岸流流速最大。
关键词:淤泥质海岸;波生沿岸流;模型验证;敏感性分析
中图分类号:U652.3;P332.4
文献标志码:A
文章编号:2095-7874(2015)03-0001-08
doi:10.7640/zggWjs201503001
收稿日期:2014-11-06
基金项目:国家高技术研究发展计划(863计划)(2012AA112509)
作者简介:张玮(1958—),男,山东青岛市人,教授,博导,主要从事港口航道工程研究。E-mail:zhangweihhu@vip.sina.com
MoveMent perfor Mance of wave-induced alongshore current on Muddy coast
ZHANG Wei1,XU Cai-guang1,QIAN Wei2
(1.College of Harbor,Coastaland Offshore Engineering,HohaiUniversity,Nanjing,Jiangsu 210098,China; 2.Jiangsu Transportation Institute Co.,Ltd.,Nanjing,Jiangsu 210017,China)
Abstract:Due to the lack ofeffective validation data and methods in the numerical simulation ofwave-induced currenton the muddy coast,we proposed a validation method called model inter-comparison.Based on two kinds ofmodel,we incorporated three-dimensionalwave-induced currentmovementequations,and carried out the research on the influence ofbeach slope and wave factorsonwave-induced alongshore currentafter validating themodel.The results shoWthat the recommended method can effectively make up for the lack of the measured data,and that although the velocity of wave-induced current on the muddy coast is relatively small,itcan still reach similarmagnitude compared to the tidal current.As the slope turns flatter,the distribution range ofalongshore currentbecomeswiderand the velocity distribution is smoother.Also,the speed and the influence scope of alongshore current increased with the incrementof incidentwave height,and the velocity of alongshore currentwill reach its maximuMwhen the incidentwave angle is45 degrees.
Keywords:muddy coast;wave-induced alongshore current;model validation;sensitivity analysis
0 引言
波浪在向近岸区域传播时,发生变形与破碎等,由于波高衰减,将驱动极其复杂的近岸水流运动,即近岸波生流,包括沿岸流、底部离岸流及裂流等。近些年随着研究深入,逐渐认识到波生流在近岸污染物扩散、泥沙输移及海岸演变等方面发挥的重要作用[1-2],并开始成为关注的热点和焦点。
波生流数值研究的基础是对波流相互作用机理的认识,目前揭示波浪对水流作用的代表性描述有两种[3]:一是“辐射应力(radiation-stress)”,以Longuet-Higgins[4-5]和Hasselmann[6]的研究工作为基础,可以帮助人们理解波浪增减水、破波拍岸、近岸沿岸流以及波流的非线性相互作用;二是
“涡流力(vortex-force representation)”,通过描述水流涡量与斯托克斯漂流相互作用,可以解释朗缪尔环流现象。辐射应力和涡流力在形式上是等价的,Garrett(1976)[7]指出涡流力理论可以从辐射应力理论中衍生出来。
在此背景下,国际上有些学者在不同模型平台上进行二次开发,引入不同波生流理论,通过模型与模型之间的对比验证来揭示某些客观存在的规律。
Zhang[8]从三维N-S动量方程出发,推导出辐射应力的垂向分布表达式,并将其应用到POM中,模拟了波生流现象。
Walstra等[9]和Lesser等[10]应用广义拉格朗日方程对原Deflt3D-flow代码进行改编,模拟了三维波生流运动。
Shchepetkin等[11]发展了三维水流ROMS模型,并将波浪破碎水滚影响引入到三维水流模型中。
Warner等[12]在SHORECIRC模型和ROMS模型基础上分别引入Mellor(2003,2005)辐射应力公式,通过三组实验对比研究了准三维和真三维模型在模拟近岸流运动时的表现和差异。
McWilliams等[13]在ROMS模型中引入涡流力理论,结合DUCK94实验研究了近岸波流运动,并与应用辐射应力来模拟波生流运动的情况进行了对比。
需要指出的是,目前有关波生流的研究多集中在沙质海岸,相对较为成熟。至于淤泥质海岸,由于岸滩坡度较缓,波生流的范围广、数值小,难以开展现场观测,也无法在实验室内加以模拟,因而缺少相关资料对于数学模型进行验证。
本文提出一种模型相互比对的淤泥质海岸波生流验证方法,基于Deflt3D和ROMS模型平台,引入相关波生流理论,分别模拟波流相互作用下的近岸流运动。在淤泥质海岸波生流缺乏实测资料的背景下,先利用沙质海岸实验资料对模型适用性进行验证,再利用这些模型针对淤泥质海岸条件模拟计算波生流,藉此进行相互比对验证。最后以淤泥质海岸为例,研究岸滩坡度和入射波浪要素对于波生沿岸流的影响,探讨淤泥质海岸波生沿岸流的水动力特性。
1 波生流计算模式简介
1.1Deflt3D波生流模型
控制方程采用基于球面坐标系的雷诺平均三维Navier-Stokes方程,垂向采用σ坐标系,并考虑静压假定和Boussinesq假设。Deflt3D模型在波流耦合计算时采用广义Lagrangian平均法(GLM)分离波浪平均和振荡运动,以实现波浪模型与潮流模型之间周期平均动量流的传递,同时在水流计算时水动力方程将以GLM方程形式求解。
本文在Deflt3D模型平台上进行二次开发,在水动力方程中引入Lin & Zhang(2004)[14]的三维辐射应力方程以体现波流相互作用,将Delft3D三维辐射应力模块改写为:
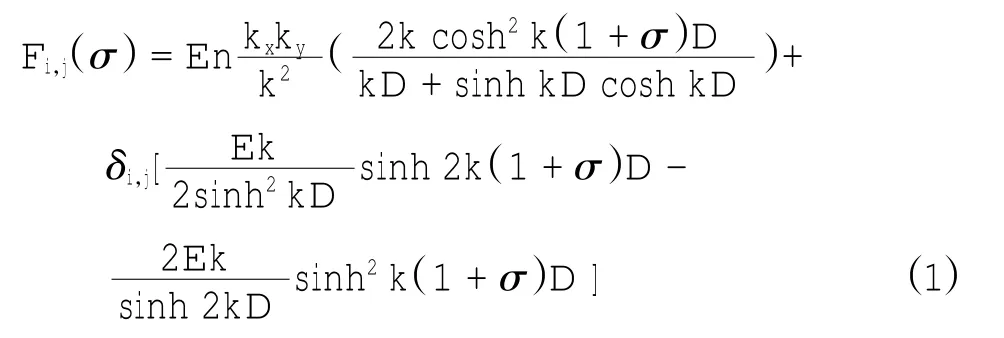
式中:E为波能;D为水深;n为波能传递率;k为波数;δ为克罗内尔标记;i,j分别代表x,y方向。
1.2ROMS波生流模型
ROMS采用垂向静压近似和Boussinesq假定,按照有限差分近似求解自由表面Reynolds平均的原始Navier-Stokes方程。模型在水平方向使用正交曲线(Arakawa C)网格,垂向采用地形拟合的可伸缩坐标系统(S坐标系)。在ROMS模型中分别引入Mellor(2011)[15]辐射应力公式和McWilliams (2010)涡流力公式(以下简称MRL10公式)。
2 模型验证
淤泥质海岸波生流实测资料匮乏,无法对所建波生流模型直接验证。为此,拟先采用沙质海岸经典波生流实验对模型进行适用性验证,然后再进行模型相互比对验证。
2.1实验数据验证
1990年,Visser[16]在Delft大学流体力学实验室建立了第一个高精度的沿岸流水槽,Visser水槽试验的目的是研究波浪斜向入射过程中的波浪破碎及其产生的沿岸流水流特征。水槽长度34.0 m,宽16.6 m,高度为0.68 m,底部采用混凝土板,试验中考虑1∶10和1∶20两种坡度,平面布置见图1。本文选取Visser试验的第四组实验为原型进行适用性验证,具体参数为:地形坡度1∶20,坡前水深0.35 m,入射波高为0.078 m,波周期为1.02 s。
由于ROMS模型及Delft3D模型模拟波流相
互作用所耦合的波浪模型均采用SWAN模型,在相同计算条件和计算参数的情况下,模拟得到的波浪场相同,所以在以后的波高对比中将只给出一种波高沿程变化图,而沿岸流分布将分别给出。波高验证结果和沿岸流平面分布如图2所示。与Visser水槽试验的成果比较,数值计算所得波高和沿岸流分布均与实测值较为吻合,近岸处产生较大流速的沿岸流,破波带外沿岸流速很低,并向离岸方向逐渐减小直至为0,说明所建模型是合理可靠的。
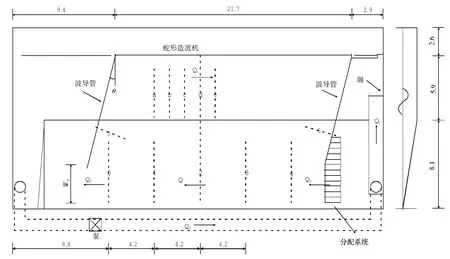
图1 Visser沿岸流波浪水槽示意图(单位:m)Fig.1 Sketch of Visser alongshore current fluMe(m)

图2 Visser沿岸流波浪水槽试验验证Fig.2 Validation of Visser alongshore current fluMe test case
2.2模型相互比对验证
2.2.1数值实验设计
对于淤泥质海岸,采用数值模型相互比对的方法进行验证。为此,在原visser沿岸流第四组试验的基础上,设计了一个假想的缓坡条件下的沿岸流运动。假想实验由原visser实验按运动学相似法则将波浪动力要素扩大50倍后得到,同时设计地形坡度由沙质海岸逐渐过渡至淤泥质海岸,以此来满足淤泥质海岸岸坡较缓的条件,创造更为真实的水流条件,假想试验基本参数为入射波高3.9 m,波周期7.21 s,入射波向15.4°,坡前水深17.5 m。
2.2.2模型相互比对验证
选取岸坡坡度1/100和1/1 000,分别代表沙质海岸和淤泥质海岸,为研究不同计算模型及计算方法之间的差异及适用性,利用Deflt3D模型和
ROMS模型分别模拟以上两种代表坡度地形上的沿岸流运动,并利用模拟结果相互比对验证。当坡度小于1/500时,需考虑波浪的沿程损耗作用,所以在波浪计算时加入collins系数,系数取值按龚崇准&戴功虎(1983)提出淤泥底海岸波浪摩阻系数值为0.01设定[17]。不同坡度时破波系数取值按李玉成(2005)提出的平缓岸坡上破碎指标(H/d)b与底坡无关设定[18],岸坡坡度大于1/100时设为0.7,小于1/100时设为0.6左右。波高模拟结果如图3所示,两种模型采用3种公式计算的沿岸流速沿程变化如图4和图5所示。
对比图4和图5的计算结果可知,Lin&Zhang公式和MRL10公式计算出的沿岸流结果相近且呈现相同的变化规律,结果合理可信。但在岸滩坡度较缓时,Mellor公式模拟沿岸流的结果则有所不同。

图3 不同坡度波高沿程变化图Fig.3 Cross-shore variation of significantwave heighton differentbeach
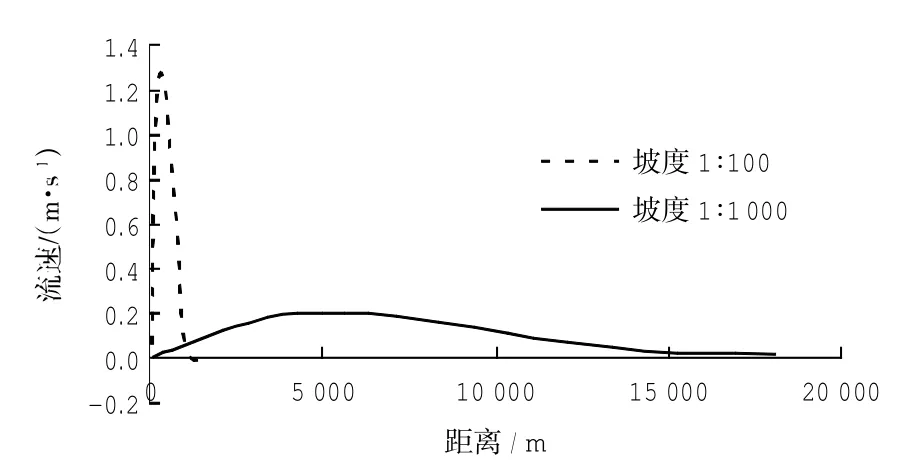
图4 Deflt3D模型计算结果图Fig.4 CoMputed result froMDeflt3D
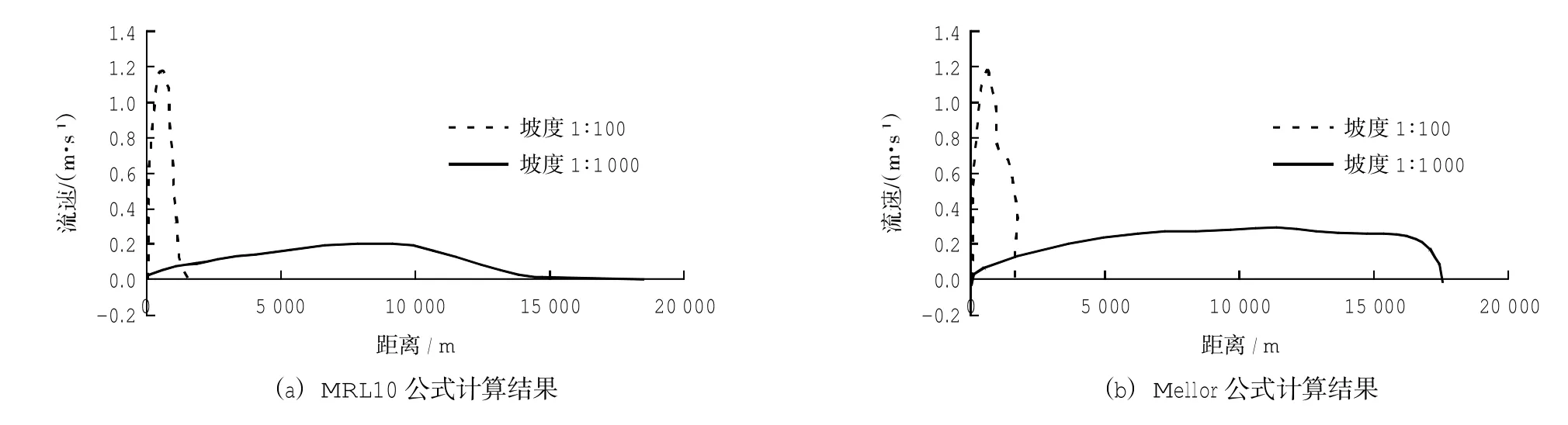
图5 基于ROMS模型两种公式计算结果对比图Fig.5 CoMputed result coMparison froMtwo kindsof equation based on ROMS
结合Visser实验可以看出,在近岸区域破波带内,沿岸流速大,当水深逐渐过渡到深水区域,沿岸流逐渐减小。但图5(b)结果显示,当岸滩坡度较缓时,Mellor公式模拟结果在深水区域仍出现较大流速的沿岸流,这一现象与实际现象不符。Ardhuin[19]通过研究波浪在变水深地形上的传播,指出应用Mellor03公式模拟近岸流运动时,在深水区也产生了平均水流,与上述现象相近,说明尽管Mellor先后在2008年和2011年对公式进行了改进,但目前看起来这个问题还是没有很好解决。由此可见,Lin&Zhang公式和MRL10公式计算结果较为合理,沿岸流分布更符合实际情况。
因此,在以下的研究中将采用ROMS模型的MRL10公式与Delft3D模型的Lin&Zhang公式进行对比分析,并相互验证。
对比Lin&Zhang公式和MRL10公式的计算结果可以看出,在沙质海岸和淤泥质海岸两种坡度地形条件下,两种公式模拟的沿岸流分布结构基本相同,波生沿岸流从外海向近岸有一个先增大再减小的过程,当岸坡坡度为1/100时,形成的沿岸流流速最大值量级都在1.2 m/s左右,而当岸坡坡度为1/1 000时,形成的沿岸流流速最大值量级都在0.2 m/s左右,仅沿岸流速最大值出现的位置有一定的差异,具体产生差异的原因还有待以后进一步研究。
以上研究结果表明,在淤泥质海岸实测资料
匮乏的情况下,采用模型相互比对的验证办法是可行的。
3 沿岸流敏感性分析
波生沿岸流主要与入射波浪要素和地形坡度有关。为研究不同因素对沿岸流的影响,以下在假想Visser试验的基础上,采用敏感性分析的办法设计了多种数值试验方案,各试验方案具体设计参数如表1所示。其中case(A~E)试验目的是为了分析不同坡度情况下沿岸流分布特性;case (D,F~H)试验目的是分析不同入射波高对沿岸流运动的影响;case(D,I~L)试验目的是分析不同入射方向对沿岸流运动的影响。
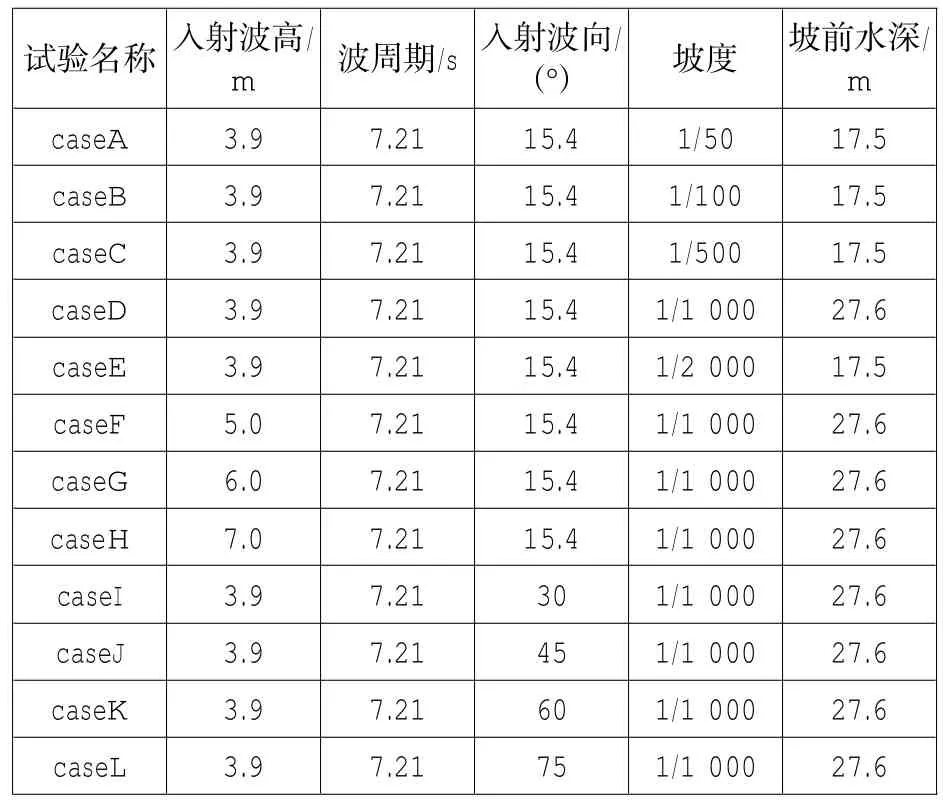
表1 各组试验主要设计参数Table 1 Basic paraMetersof different test case
3.1岸坡坡度影响
利用Lin&Zhang公式和MRL10公式分别对岸坡坡度为1/50、1/100、1/500、1/1 000和1/2 000条件下的沿岸流进行模拟计算(caseA~E),模拟结果如图6所示。分析不同坡度下沿岸流的分布情况,可以看出随着坡度的变小,破波带范围逐渐变大,产生的沿岸流范围变广,沿岸流分布趋于平缓,沿岸流流速也渐小。岸坡坡度大于1/100时,可以视为沙质海岸,近岸波浪破碎比较集中,沿岸流流速相对较大,最大流速达1.2~1.6 m/s以上,明显大于一般潮流流速;当岸坡坡度小于1/500时,可视为粉砂淤泥质海岸,波浪以沿程损耗为主,存在范围宽广的破波带,破波带内存在沿岸流现象,沿岸流数值相对较小,但1/1 000坡度地形条件下产生的沿岸流最大流速仍可以达到0.2~0.4 m/s左右,与潮流平均流速相当。
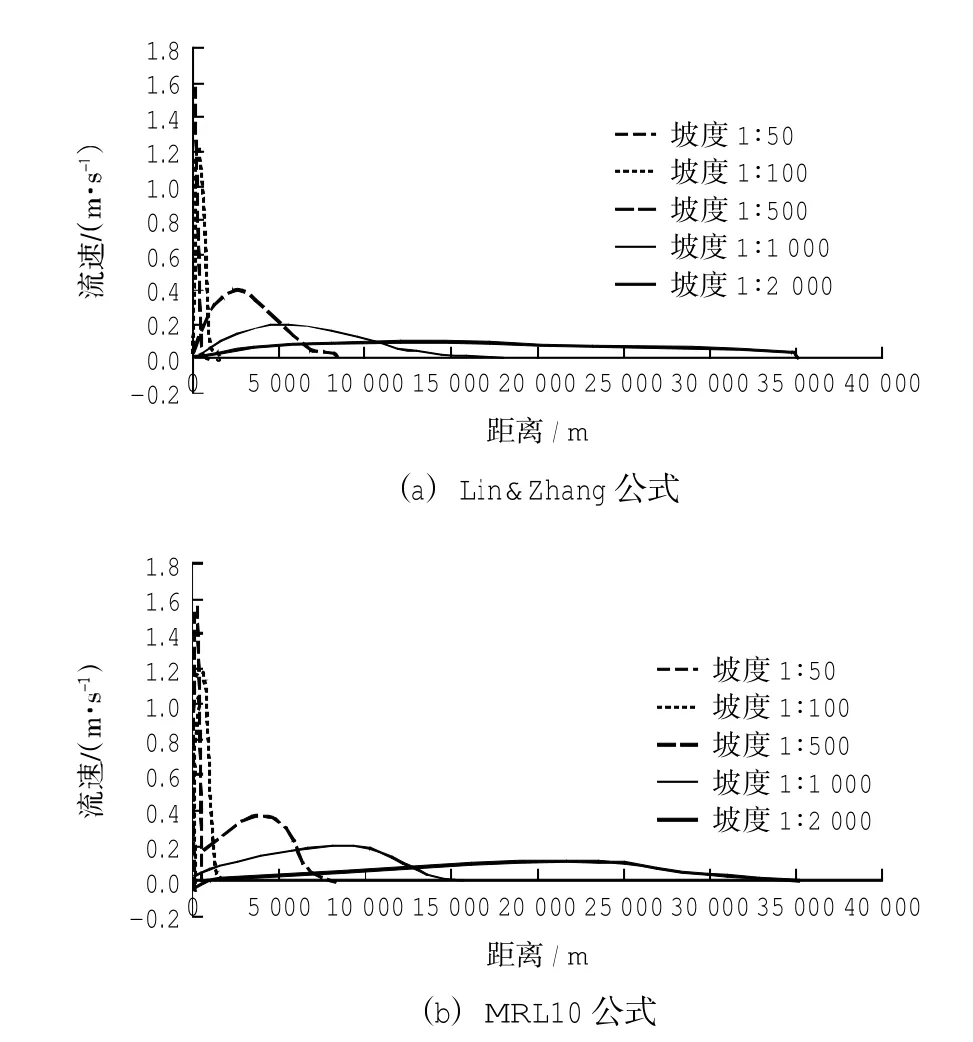
图6 不同坡度条件下两种方法计算结果对比图Fig.6 CoMparison of coMputed result froMtwo kindsof equation on differentbeach
理论分析表明,驱动沿岸流的主要因素为波生动量的沿岸分量与床面摩阻。当波浪与岸线存在入射夹角时,平面波生动量的沿岸侧向分量将驱动水体在顺岸方向产生稳定的净流动。结合不同坡度下的波高分布情况(如图7),可以看出随着坡度的变小,波高衰减越来越平缓。在沙质海岸,破波点附近的波高迅速变化产生较大的侧向动量梯度,因此沿岸流速较高;而在淤泥质海岸,破波带内的波高变化不如沙质海岸破波点附近的波高变化明显,因此产生的侧向动量梯度较小,沿岸流速较低,且随着破波带范围的扩大,沿岸流范围相应增大。
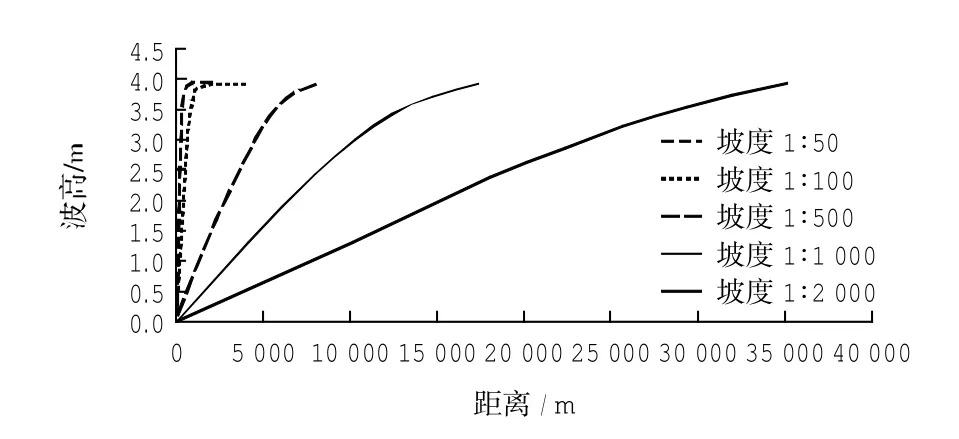
图7 不同坡度波高沿程变化图Fig.7 Cross-shore variation of significantwave heighton differentbeach
以上探讨了地形坡度对沿岸流分布的影响,由于淤泥质海岸岸滩坡度在1/1 000~1/2 000之
间,以下拟选择1/1 000岸滩坡度来研究淤泥质海岸波生沿岸流受入射波浪要素影响的一般规律。在此基础上,研究1/1 000岸滩坡度条件下具有不同入射波高和入射角度的波浪作用下的沿岸流分布情况,以此来探讨淤泥质海岸波生沿岸流的一般特性。
3.2入射波高影响
在1/1 000的缓坡地形上设计了一组入射波高分别为3.9 m、5 m、6 m和7 m的试验,以探讨淤泥质海岸条件下具有不同入射波高产生的沿岸流分布特性。
淤泥质海岸地区,外海波高衰减以沿程损耗为主,波浪破碎后,波高衰减以沿程损耗和破波损耗为主,在近岸波高衰减到一定程度后,波浪破碎达到饱和,之后近岸地区的波高沿程变化与入射波高大小关系不大(如图8)。这是因为坡度为1/1 000的海岸又称为消能型海岸,此海岸存在波浪破碎饱和现象,破碎饱和后波高变化与当地水深成线性关系。
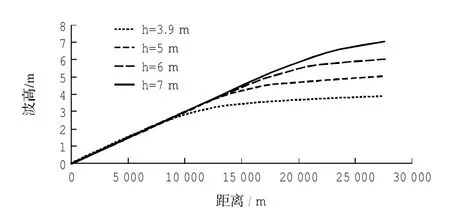
图8 不同入射波高下波高沿程变化图Fig.8 Cross-shore variation of significantwave heighton different incidentwave height
分析沿岸流的分布情况,可以看出随着入射波高增大,沿岸流流速逐渐增大,流速最大值离岸位置相应向外海移动,沿岸流强度及影响范围相对较大;与波高沿程变化相似,波浪破碎至一定区域后,沿岸流沿程变化与入射波浪波高无关。由图9可以发现,两种模型计算结果均呈现以上相同的变化规律,选取5 m波高时的沿岸流做对比(如图10),两种模型计算出的沿岸流从外海向近岸都是先增大后减小,且最大流速量级均在0.24 m/s左右,但是两种模型计算的沿岸流流速最大值出现的位置存在着明显差异,可能与两种模型引入的波生流理论或者计算模式的差异有关(如Lin&Zhang公式代表辐射应力作用,而MRL10公式代表涡流力作用;Delft3D模型是准三维模型而ROMS模型是真三维模型等),这有待进一步研究。在Deflt3D模型中,沿岸流的产生主要是由于辐射应力的作用;在ROMS模型中,Uchiyama and McWilliams[13]将波浪对水流的作用简称为WEC(WaveEffecton Current),将波浪对水流的作用力定义为WEC-Stress,沿岸流也相应在WEC-Stress的驱动下产生。
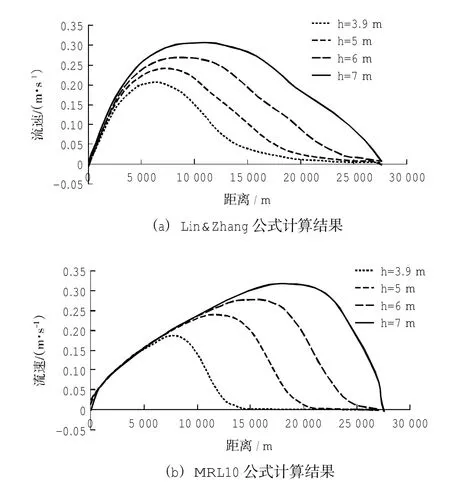
图9 不同入射波高下两种方法计算结果对比图Fig.9 CoMparison of coMputed result froMtwo kindsof Modelon different incidentwave height
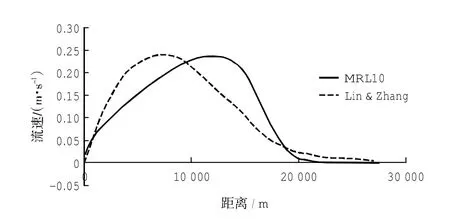
图10 波高5m时两种方法计算结果对比图Fig.10 CoMparison of coMputed result froMtwo kindsof Modelwhen incidentwave height is5m
结合图11和图12可知,Delft3D计算所得沿岸流分布与辐射应力梯度分布对应良好,变化规律一致;同理,ROMS模型计算所得沿岸流分布与WEC-Stress分布对应良好,分布规律基本与辐射应力分布规律相同。

图11 Delft3D计算辐射应力沿程变化图Fig.11 Cross-shore variation of radiation stressby Delft3D
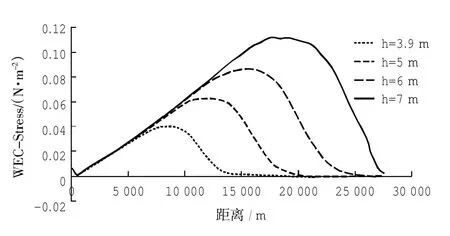
图12 ROMS计算WEC-Stress沿程变化图Fig.12 Cross-shore variation ofWEC-Stressby ROMS
3.3入射角度影响
波浪斜向入射是波浪产生沿岸流的一个重要条件,入射角度对于沿岸流的影响同样十分重要。因此,将在1/1 000的缓坡地形上研究入射波向为15.4°、30°、45°、60°和75°时沿岸流的分布情况。具体试验参数参见表1中的case(D,H~L),波高沿程变化详见图13。
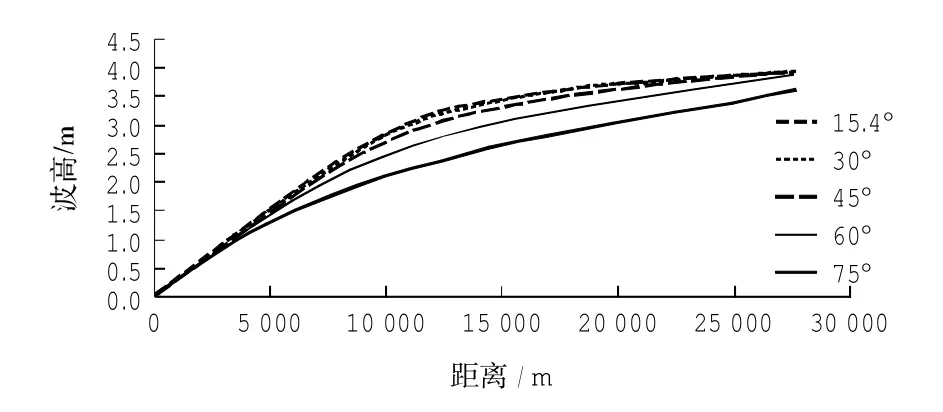
图13 不同入射波向下波高沿程变化图Fig.13 Cross-shore variation of significantwave heighton different incidentwave direction
两种模型计算所得沿岸流流速沿程变化如图14所示。可以看出,两种模型计算的沿岸流分布呈现相同的变化规律:当波浪入射角度小于45°时,随着入射波向与岸线法向夹角的增大,沿岸流流速逐渐增大,流速最大值从0.2 m/s左右增大至0.4 m/s左右,同时流速最大值离岸位置往外海移动;当入射角度增大到45°时,沿岸流流速达到最大;之后继续增大入射角,沿岸流最大值逐渐减小,流速最大值离岸位置向近岸移动。孙涛[20]和吴相忠[21]等也曾指出入射角度约为45°时沿岸流流速达到最大,这也佐证了本研究成果的正确性。
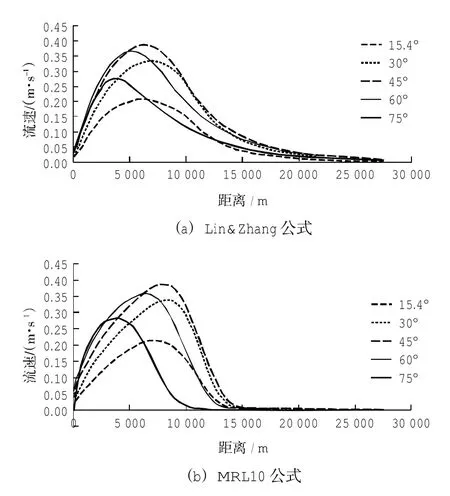
图14 不同入射波向下两种方法计算结果对比图Fig.14 CoMparison of coMputed result froMtwo kindsof Modelon different incidentwave direction
4 结论及展望
1)在淤泥质海岸波生流数值模拟缺乏实测资料验证的情况下,提出了一种模型相互比对的验证方法,经过比较,说明所提方法较为合理,可以有效弥补目前淤泥质海岸波生流实测资料匮乏的不足。
2)海岸坡度是影响波生沿岸流的重要因素。在岸坡坡度大于1/100的沙质海岸,沿岸流分布比较集中,沿岸流流速相对较大;而在岸坡坡度小于1/500的淤泥质海岸,沿岸流分布范围较广,沿岸流流速相对较小。
3)对于淤泥质海岸,近岸波浪沿程变化存在破碎饱和现象;且随入射波高增加,流速最大位置往外海方向移动,产生的沿岸流强度及影响范围也相应较大。
4)当波浪入射角度为45°时,产生的沿岸流流速最大。当入射角度小于45°角时,随入射角度的增大,沿岸流速逐渐增加,流速最大值位置向外海移动;当入射角度大于45°时,随入射角度的
增大,沿岸流速逐渐减小,流速最大值位置往近岸移动。
5)研究表明,波高为3.9 m的入射波,在沙质海岸条件下,沿岸流流速可以达到1.2~1.6 m/s,大于一般潮流流速;在淤泥质海岸条件下,沿岸流流速可以达到0.2~0.4 m/s,与潮流平均流速相当。因而在淤泥质海岸水动力条件研究中,波生流的影响不容忽略。
在模拟淤泥质海岸波生沿岸流运动时,分别采用了基于辐射应力公式和涡流力公式的两种模型,虽然得出相同的变化规律,但是模拟结果之间仍存在一定的差异。在接下来的工作中,将进一步研究这种差异产生的原因,进而更深刻地认识波流相互作用机理和波生流的运动特性。
参考文献:
[1]解鸣晓,张玮.近岸波生流运动三维数值模拟及验证[J].水科学进展,2011(3):391-399. XIE Ming-xiao,ZHANG Wei.3D numericalmodelingofnearshore wave-induced currents[J].Advances in Water Science,2011(3): 391-399.
[2]解鸣晓.淤泥质海岸波生流动力机制及三维模拟研究[J].泥沙研究,2012(6):11-18. XIE Ming-xiao.MechanisMand three-dimensional numerical modelling of wave-induced currents on mudflats[J].Journal of SedimentResearch,2012(6):11-18.
[3] LANE E M,RESTREPO JM,MC WILLIAMS JC.Wave-current interaction:a comparison of radiation-stress and vortex-force representations[J].J.Phys.Oceanogr,2007,37:1 122-1 141.
[4] LONGUET-HIGGINS MS,STEWART R W.Radiation stress and mass transport in gravitywaves,with application to"surfbeats."[J]. J.Fluid Mech.,1962,13:481-504.
[5] LONGUET-HIGGINS MS,TEWART R W.Radiation stresses in waterwaves:A physicaldiscussion,with applications[J].Deep-Sea Res.,1964,11:529-562.
[6] HASSELMANN K.On the mass and momentuMtransfer between short gravity waves and larger-scale motions[J].J.Fluid Mech., 1971,50:189-201.
[7] GARRETTC.GenerationofLangmuircirculationsbysurfacewaves-A feedbackmechanism[J].J.Mar.Res.,1976,34:116-130.
[8] ZHANG Dan.Numerical simulation of large-scale wave and currents[D].Singapore:NationalUniversity of Singapore,2004.
[9] WALSTRA D JR,ROELVINK JA,GROENEWEG J.Calculation ofwave-driven currents in a3D mean floWmodel[C]//EDGE B L. Proceedings of the 27th coastal engineering international conference 2000.NeWYork:American Society of Civil Engineers,2000: 1 050-1 063.
[10] LESSER G R,ROELVINK JA,VAN KESTER JA T M,etal.Development and validation of a three-dimensional morphological model[J].CoastalEng.,2004,51:883-915.
[11] SHCHEPETKIN A F,MC WILLIAMS JC.The regional oceanic modeling systeM(ROMS):a split-explicit,free-surface,topography-following-coordinateoceanicmodel[J].OceanModelling,2005, 9:347-404.
[12] HAAS K A,WARNER JC.Comparing a quasi-3D to a full 3D nearshore circulation model:SHORECIRC and ROMS[J].Ocean Modelling,2009,26:91-103.
[13] UCHIYAMA Y,MC WILLIAMSJC,SHCHEPETKIN A F.Wavecurrent interaction in an oceanic circulation modelwith a vortexforce formalism:Application to the surf zone[J].Ocean Modelling, 2010,34:16-35.
[14] LIN P,ZHANG D.The depth-dependent radiation stresses and theireffecton coastal currents[C]//Proceedings of the 6th international conference on hydrodynamics:hydrodynamics VI theory and applications.2004:247-254.
[15] MELLOR G L.Wave radiation stress[J].Ocean Dynamics,2011, 61:563-568.
[16] VISSER P J.Laboratory measurements of uniforMlongshore currents[J].Coastal Engineering,1991,15(5-6):563-593.
[17]龚崇准,戴功虎.浅水波浪变形数学模型与淤泥质海岸底摩擦系数的确定[J].海洋工程,1983(3):21-33. GONG Chong-zhun,DAIGong-hu.Mathematicalmodel for wave deformation in shoaling water and determination of bottoMfriction ofsiltbeach[J].TheOcean Engineering,1983(3):21-33.
[18]肖辉.波浪在缓坡上的变形及破碎[D].大连:大连理工大学,2005. XIAO Hui.Thewave transformation and breaking on gentle slopes [D].Dalian:Dalian Universityof Technology,2005.
[19] ARDHUIN F,JENKINS A D,BELIBASSAKIS K A.2008a:Comments on "The three-dimensional current and surface wave equations."[J].J.Phys.Oceanogr.,2008,38,1 340-1 350.
[20]孙涛,陶建华.波浪作用下缓坡近岸海域沿岸流分布影响因素分析[J].水动力学研究与进展:A辑,2004,19(4):558-564. SUN Tao,TAO Jian-hua.Influence factorsofwave-induced longshore currenton anear-shoremild slope beach.Journalof Hydrodynamics:A,2004,19(4):558-564.
[21]吴相忠.近岸流的三维数值模拟研究[D].天津:天津大学,2010. WU Xiang-zhong.Three-dimensional numerical simulation of nearshore current[D].Tianjin:Tianjin University,2010.
