移相器量化误差对相控阵天线相位中心的影响分析

陈曦　杨龙　傅光　龚书喜

(1.西安电子科技大学 天线与微波技术重点实验室,西安 710071;

2.西安电子科技大学信息感知技术协同创新中心,西安 710071)



移相器量化误差对相控阵天线相位中心的影响分析

陈曦1,2杨龙1傅光1,2龚书喜1,2

(1.西安电子科技大学 天线与微波技术重点实验室,西安 710071;

2.西安电子科技大学信息感知技术协同创新中心,西安 710071)

摘要为精确预测相控阵天线相位中心的特性,研究了数字移相器相位量化误差对相控阵天线相位中心的影响．对计算相控阵天线相位中心的方法进行了论述,得出了根据远场相位分布精确计算天线阵相位中心的方法;采用该方法对一算例阵列进行计算仿真,算例阵列采用5位数字移相器,计算得出不同扫描角下天线相位中心的变化．计算结果表明:数字移相器量化误差对相控阵天线相位中心可造成显著影响,该影响与移相器位数和扫描角均有关．研究结论可用于指导高精度相控阵天线的设计．

关键词相控阵天线;相位中心;数字移相器;量化误差;扫描角

资助项目: 中央高校基本科研业务费项目(No.K5051202006，No.WRYB142104)； 西安市科技计划项目(CXY1436②)

联系人： 陈曦 E-mail：xchen@mail.xidian.edu.cn

引言

相控阵天线已经被广泛地应用于各种雷达系统,随着对雷达系统的跟踪及定位要求的提高,在某些情况下,仅靠主瓣波束的幅度特性来搜索定位已不能满足精度要求,必须以阵列天线的相位中心为参考基准进行精确定位和测量[1]．对于寻找天线相位中心的研究,前人已做了一些研究并得出一些有效的结论,但大多数都是针对单天线的研究[2-4],如微带天线、喇叭天线、对数周期天线等．而关于阵列天线相位中心的研究甚少,早期有几篇文献[5-6],对理想的相控阵天线相位中心进行了研究．近年来,文献[7-8]做了相关的研究,对理想相控阵天线的精确计算方法进行了研究,并对计算结果进行了误差分析．

相控阵天线大都采用数字移相器控制波束扫描方向,而数字移相器会造成激励相位的量化误差,这种量化误差会使相控阵天线增益受损、旁瓣抬高、主瓣展宽、波束指向发生偏差等性能下降,尤其表现在对使用精度要求较高的场合．相控阵天线的相位中心属于高精度的天线指标,相位中心的微小偏移量可造成雷达定位的显著偏差．本文结合相控阵天线设计中的实际需要,采用理论分析和仿真计算的方法,研究移相器量化误差对相控阵天线相位中心造成的影响,所得结论可用于相控阵天线的工程实践．

1理论分析

1.1　相控阵天线的相位方向函数

假设有一个n元阵,所有阵元为相似元,则将所有单元的远区辐射场直接相加,可得天线阵总辐射场表达式

(1)

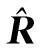
(2)

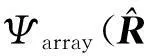
(3)

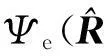
1.2　相控阵天线的相位中心计算方法

相位中心是天线阵上或其周围的一个参考点,该点可使远区辐射场的相位值基本是一常数．根据该定义可建立相位方向函数与相位中心的关系．

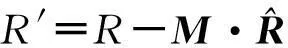
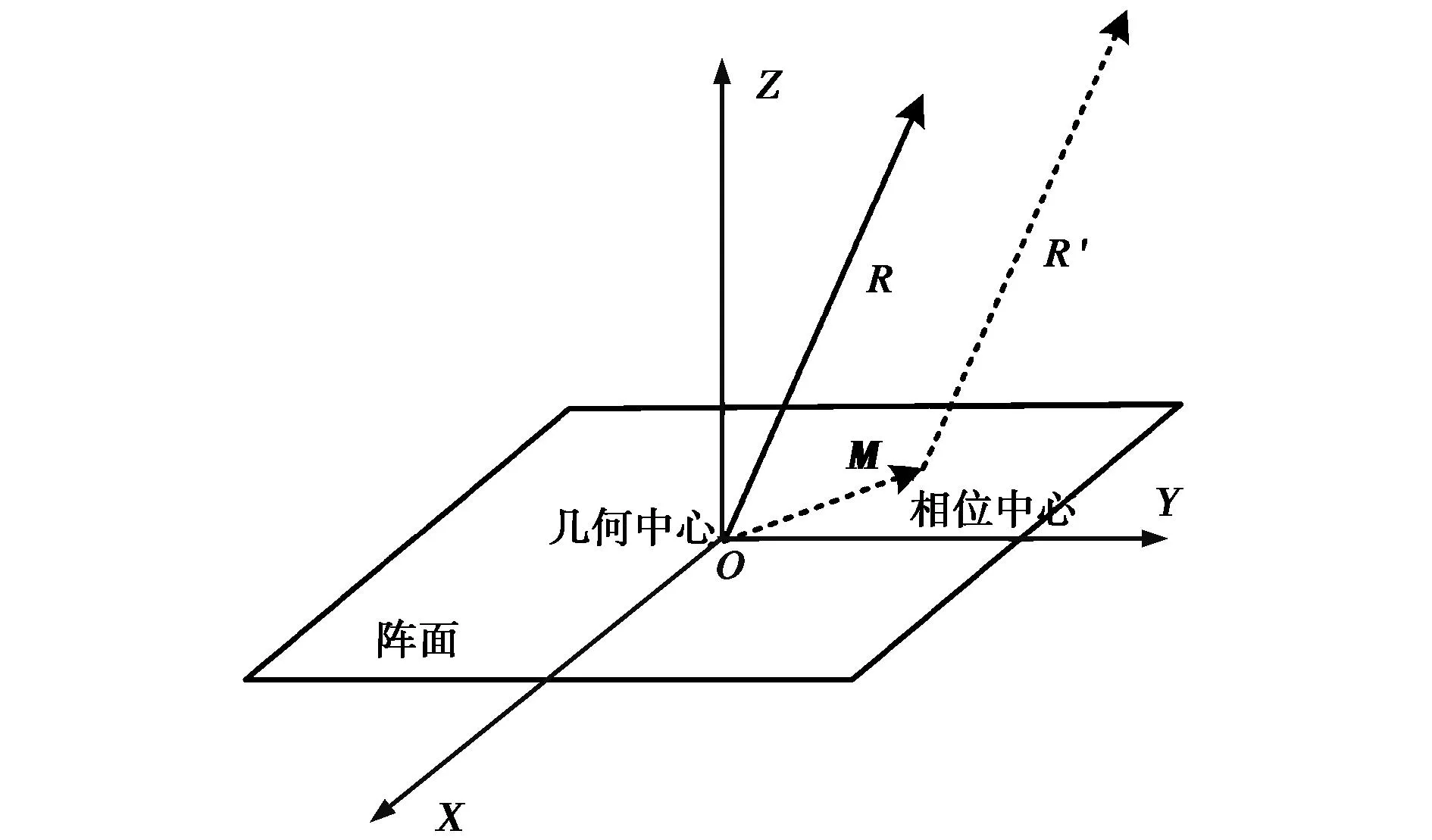
图1　阵列天线相位中心偏移示意图

(4)

对比式(4)和式(1)可以得出相位方向函数与相位中心M的关系为

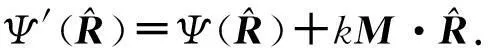
(5)

(6)

将其代入式(5)可以得到

(7)

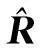
(8)

在图2所示的直角坐标系中,式(8)中矢量可表示为

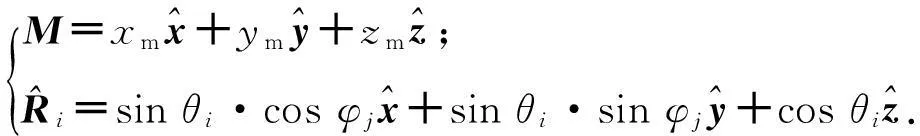
(9)

则

ym·sinθi·sinφj+zm·cosθi)-C]2.

(10)

图2　直角坐标系

当天线的口面场沿X轴或Y轴分布时,φ=0°或90°对应方向图主平面．此时,式(10)可简化为式(11)．其中,φ=0°时,tm取xm;φ=90°时,tm取ym．

zm·cos(θi))-C]2.

(11)

求使ε取得最小值的解．式(11)两边分别对tm、zm、C求导,并令ε的偏导数为0,可得方程组

(12)

解方程组(12)可得矩阵表示为

(13)

根据式(13)可求出主平面内的二维相位中心,以及相位中心置于参考系原点时的相位分布起伏的基准值C．再根据多个主平面内的二维相位中心可计算出三维相位中心．

1.3　移相器相位量化误差分析

从相位方向函数的表达可以看出,远区相位分布与阵元的相位方向函数、阵列幅相激励、阵元的位置以及工作频率都有关．当阵列结构和工作频率确

定,天线的相位分布主要取决于阵列的幅相分布．

在相控阵天线的实际设计中,移相器的配相值通常并不能连续配给,大多数都会采用有限位数的移相器,有限位数移相器提供的相位值是离散的,所需相位值只能就近选择,这就是相位量化;而量化值与理想值之间存在一个差值,称之为相位量化误差．相位量化误差是一种近似处理,它会使阵列的相位激励无法取得实际值,造成远场幅度和相位方向图发生变化,进而影响天线阵的相位中心．

有限位的数字移相器会造成相位量化误差,若移相器位数为N,则最大相位量化误差为

α=π/2N.

(14)

即每一个单元的实际馈相值与理论值的相差不会超过π/2N．这种误差是一种系统误差,可以通过计算或测量提前获知．

2实验结果分析

采用上述计算方法,以一个14×20元的矩形栅

格平面相控阵为算例研究移相器量化误差对相位中心的影响,单元采用理想点源．图3是阵列结构示意图,阵元间距取为0.454λ0(X方向)×0.567λ0(Y方向)．

图3　阵列结构示意图

阵元幅度采用均匀分布,俯仰面扫描采用5位数字移相器,则最小相位增量为11.25°,可以得到的相位增量如表1．方位面采用连续相位变化．

如图4所示,定义俯仰面和方位面为过方向图主瓣的两个正交面,若俯仰面内的扫描角范围为[-13°,37°],当波束在俯仰面内扫描的指向角为θelev=-13°、θazim=0°时,俯仰向单元的理论配相值和实际配相值列在表2中,曲线画于图5．

表1　可用的相位增量

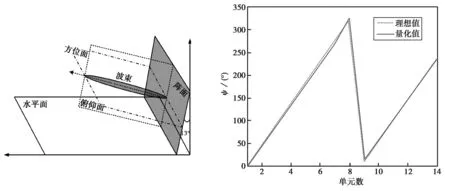
图4　阵列工作状态示意图　　　　　　　　图5　理论值与量化值对比曲线

单元序数1234567理论配相/(°)045.9170191.83402137.751183.668229.585275.5021实际配相/(°)04590135180225270单元序数891011121314理论配相/(°)321.41917.33607453.2530899.17009145.0871191.0041236.9211实际配相/(°)326.2511.2556.25101.25146.25191.25236.25

从表2可以看出:理论配相的相差是45.917 01°;实际配相的相差除了在单元7和8之间的相差为56.25°外，其余相差均为45°．对于所有阵元，实际配相值和理论的差最多不超过5.502 1°.图6给出主瓣3dB区域内相位分布以及相位均方差ΔΨ,

(15)

图6中ΔΨ=8.385 8×10-15°．计算得相位中心位于(7.791 8×10-12λ0,-2.239 5×10-16λ0,-3.310 5×10-11λ0)．可见,俯仰角-13°时,相位分布平坦,相位中心几乎没有变化．

对θazim=0°平面内有限个俯仰角进行计算,结果列于表3中．

图6　主瓣内相位分布

表3　俯仰面内扫描时的ΔΨ和相位中心

从计算结果可看出,当俯仰角扫描至-5°和5°时,相位中心发生了较大变化,ΔΨ也较大．对扫描角-5°的状态进行分析,其实际配相值和理想值进行对比列于表4中．表4中显示,理论相差应为17.790 23°,而实际配相的相差以22.5°和11.25°交替变化．这主要是因为理论相差17.790 23°接近实际配相的两个相邻相差的中间值,即(22.5°+11.25°)/2=16.875°,所以在相位递增过程中会产生相邻相差被交替选取的情况．从相位曲线对比图(图7(a))也可以看出这种交替现象．

表4　俯仰角-5°时理论值和实际值对比

表4中实际配相值和理论值的最大差值不超过5.491 4°．可以预计,5位数字移相器可提供最小相差11.25°,则任何情况下,理论值和实际值的相差都不会超过11.25°/2=5.625°．如果要求相位中心稳定,相位量化误差应减小,移相器位数应有所提高,但馈电网络的复杂度和成本将会提高,因此应该结合系统要求综合考虑．同样在俯仰角5°时也发生了馈相交替变化(图7(b))．

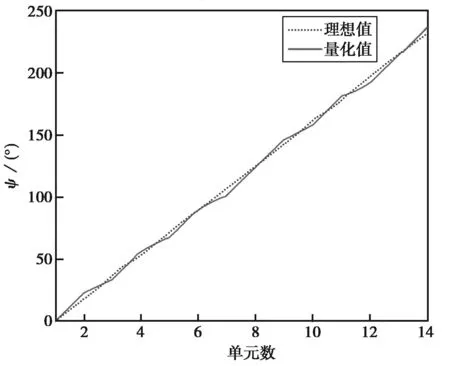
(a) θelev=-5°时

(b) θelev=5°时图7　俯仰向单元馈相理论值与量化值对比曲线

3结论

本文通过对相控阵天线的理论分析,建立了相控阵天线相位中心与相位方向函数的关系,并进一步研究了移相器量化误差对相控阵天线相位中心的影响．通过对相控阵天线相位中心的仿真实验,可以得出以下几个结论:

1) 移相器量化误差会造成相位中心偏移;

2) 较大的相位量化误差会造成较大相位中心偏移量,由移相器位数和扫描角共同决定,当相邻阵元的相差出现交替取值时,相位中心发生最大偏移;

3) 造成的Z向偏移量远大于X、Y向偏移量．

采用本文提出的计算方法,可以定量分析数字移相器位数对相控阵天线相位中心影响的程度,进而可指导相控阵天线应用中数字移相器的选择．

参考文献

[1]尚军平, 傅德民, 邓颖波. 天线相位中心的精确测量方法研究[J]. 西安电子科技大学学报, 2008, 35(4): 673-677.

SHANG Junping, FU Demin, DENG Yingbo. Research on the accurate measurement method for the antenna phase center[J]. Journal of Xidian University, 2008, 35(4): 673-677. (in Chinese)

[2]KUMAR A, SARMA A D, ANSARI E. Improved phase center estimation for GNSS patch antenna [J]. IEEE Transactions on Antennas and Propagation, 2013, 61(4): 1909-1915.

[3]唐璞, 李欣, 王建, 等. 计算天线相位中心的移动参考点法[J]. 电波科学学报, 2005, 20(6): 725-728.

TANG Pu, LI Xin, WANG Jian, et al. Calculation of phase center for the antenna with the method of moving reference point[J]. Chinese Journal of Radio Science, 2005, 20(6): 725-728. (in Chinese)

[4]金元松, 任晓飞, 冀海鸣, 等. 对数周期偶极子天线全空间可变相位中心[J]. 电波科学学报, 2007, 22(2): 229-233.

JIN Yuansong, REN Xiaofei, JI Haiming, et al. Variable phase center of the log-periodic dipole antenna in full space [J]. Chinese Journal of Radio Science, 2007, 22(2): 229-233. (in Chinese)

[5]TAGGART D, SACKS L. The calculation of the phase center for spacecraft phased array antennas [J]. MILCOM, 1995, 3: 1046-1050.

[6]MOWLER M, LINDMARK B. Estimation of mutual coupling, element factor, and phase center of antenna arrays [C]//2005 IEEE Antennas and Propagation Society International Symposium. July 3-8, 2005, 4B: 6-9.

[7]陈曦, 傅光, 龚书喜, 等. 阵列天线相位中心的计算与分析[J]. 电波科学学报, 2010, 25(2): 330-335.

CHEN Xi, FU Guang, GONG Shuxi, et al. Calculation and analysis of phase center on array antennas [J]. Chinese Journal of Radio Science, 2010, 25(2): 330-335. (in Chinese)

[8]陈曦, 傅光, 龚书喜, 等. 阵列天线相位中心的校准方法研究及其误差分析[J]. 西安电子科技大学学报,2011, 38(3): 145-149.

CHEN Xi, FU Guang, GONG Shuxi, et al. Study of calibration of the phase center of array antennas and its error analysis [J]. Journal of Xidian University, 2011, 38(3): 145-149. (in Chinese)

陈曦(1983-),男,陕西人,西安电子科技大学电磁场与微波技术专业讲师,博士,主要从事阵列天线理论与技术、宽带小型化天线理论与技术研究．

杨龙(1988-),男,湖南人,西安电子科技大学电磁场与微波技术专业博士研究生,主要从事阵列天线技术、宽带小型化天线技术研究．

傅光(1963-),男,陕西人,西安电子科技大学电磁场与微波技术专业教授,主要从事微带天线、宽带线天线、阵列天线理论与技术的研究．

Effect analysis of phase quantization error of phase shifter on

phase center of phased array antenna

CHEN Xi1,2YANG Long1FU Guang1,2GONG Shuxi1,2

(1.ScienceandTechnologyonAntennaandMicrowaveLaboratory,XidianUniv,

Xi’an710071,China;2.CollaborativeInnovationCenterofInformationSensingand

Understanding,XidianUniversity,Xi’an710071,China)

AbstractIt is researched the effect of digital phase shifter quantization errors on the phase center of phased array antenna in the paper. Firstly, the method of calculating phase center of phased array antenna is presented. The phase center of phased array antenna can be calculated accurately according to the phase distribution at far field. Secondly, the simulation based on the proposed method is carried out on a example array with 5 digital phase shifter, and the variation of the phase center on different scan angles is acquired. The calculating results indicate the digital phase shifter quantization errors of the phased array antenna can make an obvious effect on its phase center, moreover, the effect is closely related to the phase shifter digit and scan angle. The conclusion can be used in designing of high-precision phased array antenna.

Key wordsarray antennas; phase center; digital phase shifter; quantization errors; scan angle

作者简介

收稿日期：2015-01-31

中图分类号TN821

文献标志码A

文章编号1005-0388(2015)06-1175-07