基于MSC.Nastran的某校车车身结构的模态分析

王若平， 刘圣仲

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)



基于MSC.Nastran的某校车车身结构的模态分析

王若平， 刘圣仲

(江苏大学 汽车与交通工程学院，江苏 镇江 212013)

应用有限元前后处理软件Patran对车身骨架进行有限元建模，然后导入MSC.Nastran进行无阻尼自由振动状态下的模态研究，得到该校车车身骨架结构有限元模型的模态,并对得到的理论模态参数进行分析，为该车车身骨架的设计方案提供全面的评价。

校车；车身骨架；模态分析；MSC.Nastran

2012年4月，国家质量监督检验检疫总局、国家标准化管理委员会制定了《专用校车安全技术条件》(GB24407—2012)和《专用校车学生座椅系统及其车辆固定件的强度》(GB24402—2012)两项强制性国家标准。这两项标准对校车安全性能的要求有了很大提升，特别是对车身结构强度的要求。

作为校车车身最为重要的参数之一,模态参数数据可以采用计算和模态参数识别试验两种方法来获取。但是对于体积庞大、结构复杂的校车车身骨架,采用试验方法进行模态分析具有周期长、成本高等局限，而且产品进行优化设计后还需重新进行试验，因此目前普遍使用计算的方法进行模态分析。模态分析是动态分析的基础和重要内容。在行驶过程中,校车车身结构在各种振动源的激励下会产生振动,如发动机运转、高速行驶时的风力，以及路面不平引起的振动等。这些振源的激励频率如果接近于车身整体或局部的固有频率就会产生共振,出现剧烈振动和噪声,甚至造成结构破坏[1]。为提高汽车的安全性、可靠性和舒适性，必须对车身结构的固有频率进行分析,通过对结构的优化设计来避开各种振源的激励频率。据有关研究表明：车身的动刚度在最近几十年来得到了很大提高，而车身的质量却呈现一定程度的下降，这正是得益于有限元法和模态分析在汽车设计中的成功应用[2-15]。本文采用有限元软件MSC.Nastran对某校车进行模态分析,并对其动态性能进行评价。

1 车身骨架有限元模型的建立

1.1 车身骨架几何模型的建立

利用Pro/E Wildfire5.0 软件[7]建立车身骨架的三维实体模型。实体模型建立之后，将其导入到Hypermesh[8]，通过软件的提取中面功能得到车身骨架的中面模型，然后经过几何清理得到车身骨架的最终三维实体模型，如图1所示。

1.2 单元的选取

通过有限元分析软件NASTRAN建立车架的三维有限元模型。由于校车车身骨架结构复杂、计算量大，因此选用三维板壳单元(SHELL)模拟车架，用梁单元(BEAM)模拟车身骨架前后侧围。

1.3 网格划分

采用混合网格划分的方式划分网格。车架结构部分采用四边形单元划分，以获得好的网格质量，减少单元数目；对于几何形状复杂的区域，充分利用三角形单元适应性强的优点，采用三角形网格。考虑到计算精度和准确性，网格单元尺寸选择30～50 mm，本次建模把单元尺寸设置为50 mm。划分好后的模型有5 015个节点。建立的有限元模型如图2所示。

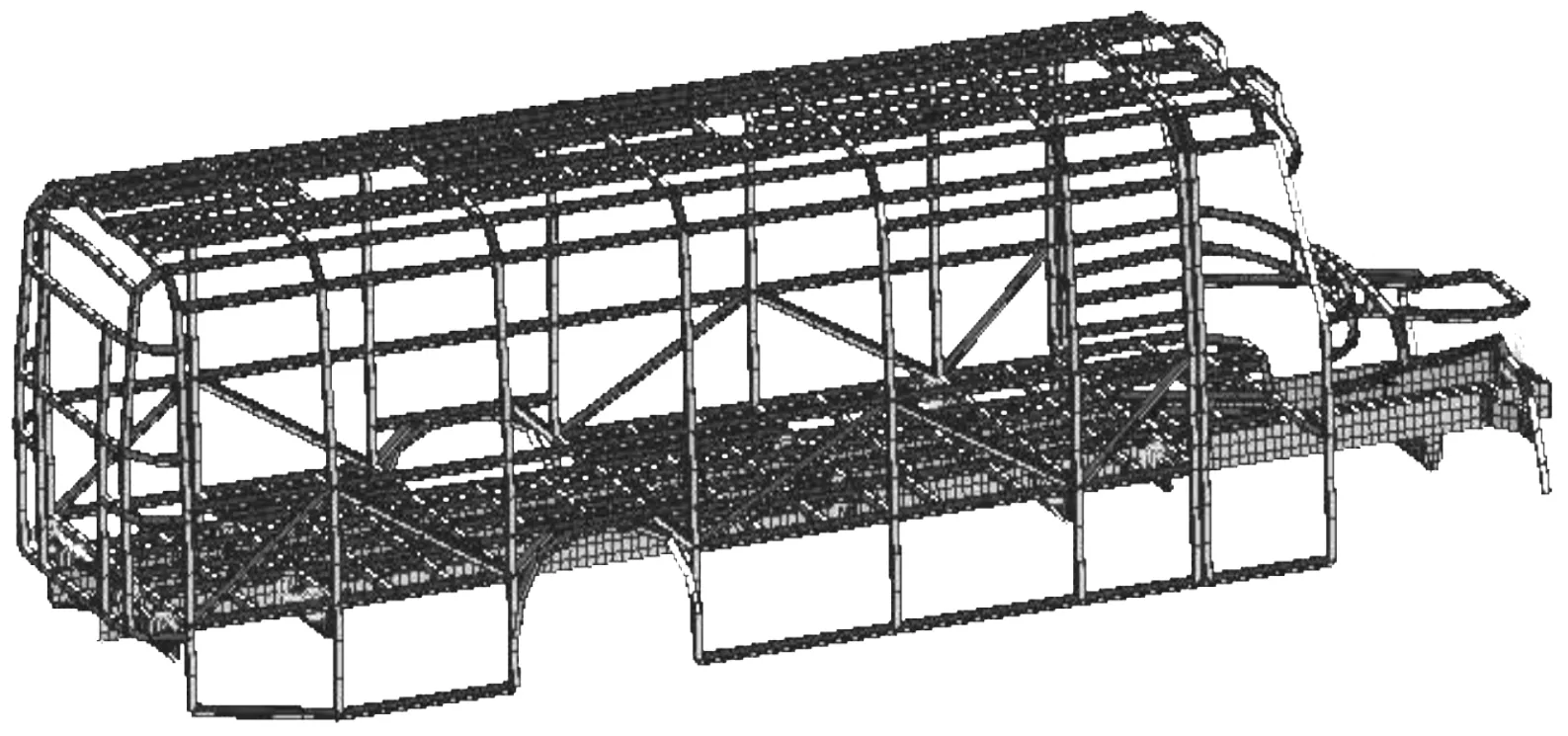
图2 车身骨架有限元模型

1.4 材料模型的建立

在有限元前处理过程中进行单元材料属性赋值时，所选材料的类型特征应与实际情况相符。本文研究的校车车身骨架使用KQJ和KQF系列冷弯型钢，这种材料可看作是各向同性材料，其力学性能见表1[9]。

校车车架横梁、纵梁等使用的材料为Q345系列钢型，其力学性能见表2。

表1 车身骨架材料的力学性能

表2 校车车架横梁、纵梁等使用的材料的力学性能

2 模态分析的理论基础

由振动理论可知，在初始激励作用下，无阻尼单自由度系统将以自身的固有频率在某一种自然状态下进行自由振动。而多自由度系统的自然状态是指整个系统在运动过程中所存在的某一位移形状。多自由度系统在振动过程的位移形状具有多样性，其种类数量与整个系统的自由度数量一致，这些位移的形状即为系统的固有振型。当系统受到来自于外界的激励时，将按照其中一种固有振型进行简谐振动。在振动过程中，系统各个质点具有同步性，并且相互之间的位移比例保持不变。每一阶振型都对应一个固定频率，因此可以用振型和固有频率来表示系统的振动特性，所以模态分析又称无阻尼自由振动系统的特性分析[12-13]。

有限元分析求解中有很多常用、高效的算法,例如NewMark方法、直接叠加法和子空间迭代法等。对于具有有限个自由度的线弹性系统，根据达朗贝尔原理,可以推得动力平衡方程为[6]

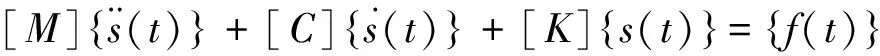
(1)

式中： [M] 为系统的质量矩阵； [K] 为系统的刚度矩阵； [C] 为系统的阻尼矩阵；f(t) 为系统的激励力向量；s(t) 为系统的位移响应向量。

如果阻尼矩阵 [C] 满足Fawzy条件，即 [K][M][C] = [C][M]-1[K],则振动系统为黏性比例阻尼系统，也称为比例阻尼系统。当此系统拥有有限个自由度时，其振动方程可用式(1)来表示。式(1)是由系统的物理坐标所描述的耦合方程组，将式(1)进行傅里叶变换可得到新的微分方程：

(2)

则可求得系统第i点的响应为

(3)

式中：φij为第i测点第j阶模态振型的系数；qj(η) 为第j阶模态坐标。

将 {φ}j记为系统的第j阶模态向量，它由系统中n个点的振型系数所组成的列向量组成，其中：

(4)

模态矩阵 [φ] 由系统各阶模态向量组成，其中：

(5)

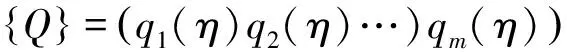
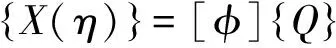
(6)

将式(2)代入式(6)有

(7)

若系统为无阻尼自由振动系统，则式(7)可改写为

(8)

式 (8)有解的条件为

(9)

由式 (9)可求得系统的固有振动频率为fi=ηi/2π。将fi代入式 (7)即可求得系统的固有振型 {φ}i。通常用子空间迭代法求解式 (9)中的特征值。为了求得正则坐标下的主振型，还需将固有振型 {φ}i正则化处理。

3 车身骨架自由模态分析和优化建议

3.1 基于MSC.Nastran的自由模态分析

校车车身的模态分析主要是求解车身结构的固有频率和固有振型，可在车身骨架无阻尼的自由振动状态下求解。求解时既不考虑车身刚度和惯性与变速箱、发动机等部件的相互耦合作用，也不考虑乘员及车载行李的质量，只考虑车身骨架的质量。 但是对于这种结构复杂、多自由度的大型车架系统,想要一一求解出其固有振型向量和所对应的固有频率是很困难的。而在其动态响应中，系统较低的几阶振型向量和固有频率就能直观地反映其振动特性,故在研究系统的动态响应时,只需要求解前几阶的固有频率和振型向量。因此，要对车身骨架的计算模态进行反复甄别，找出最能反映车身整体振动的几阶模态[10]。本文在MSC.Nastran软件中选用兰索斯(Lanczos)方法作为特征值求解法，提取校车车身骨架的前10阶模态振型，如表3所示。第1～3阶模态见图3～5。

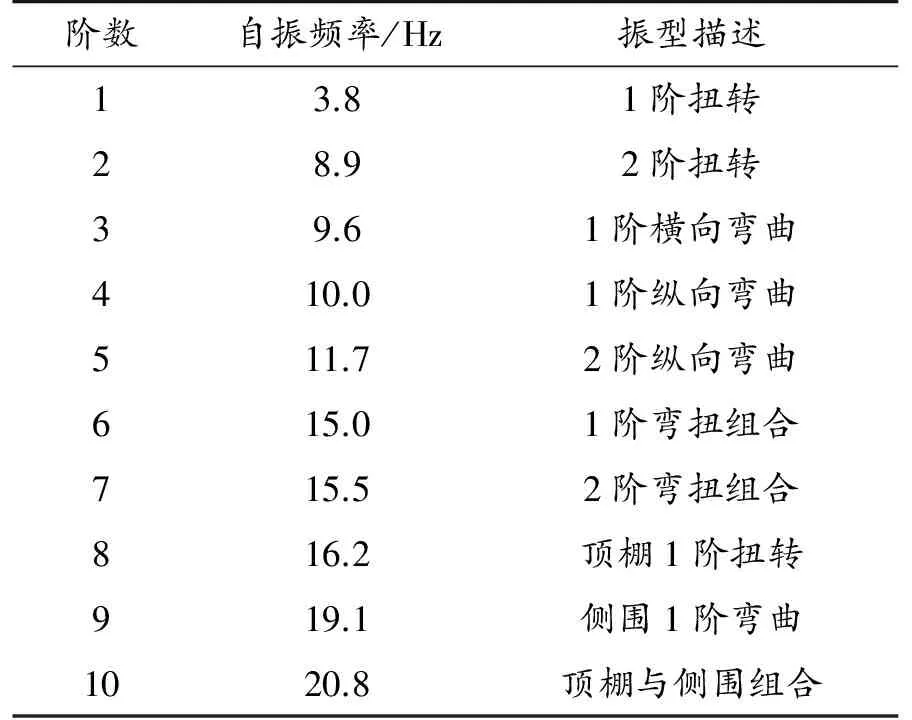
表3 校车车身骨架的前10阶模态振型

3.2 模态分析结果分析

由模态分析结果可知，校车的前10阶固有频率值为3.5～15.5 Hz。在校车正常行驶过程中，车身受到的主要激励源有车轮不平衡引起的转动、发动机运转、传动轴的不平衡以及路面不平等[12]。就目前国内高速公路和城市柏油路面而言，车速在100 km/h时，激振频率小于3 Hz，激励分量较大。车轮不平衡产生的激振频率一般小于11 Hz，考虑到现代轮辋制造工艺水平较高，此激励分量可以忽略不计。校车在城市中车速往往为40～80 km/h，高速公路上的行驶车速为100～120 km/h，因传动轴不平衡所产生的激振频率一般为33～68 Hz[9]。该校车采用六缸柴油机，额定发动机怠速工况转速为700 r/min。

(10)

式中：i为发动机汽缸数；ne为发动机转速(r/min)。

由式(10)计算得到发动机的怠速激振频率为35 Hz。由前面的分析可知：车身骨架的前10阶理论固有频率应该介于3～35 Hz，这样才能保证车身骨架具有良好的振动特性。同时，1阶弯曲模态频率和1阶扭转模态频率要相差3 Hz以上，以避免出现耦合效应。从模态分析的结果来看，校车车身前10阶固有频率为3.5～15.5 Hz，错开了激励分量较大的激振频率，车身结构不会发生共振现象。由于本文建模时省去蒙皮以及一些非承载结构，所以计算出的车身骨架的理论固有频率要低于实际值。但从总体上来说，该车车身骨架的动态性能良好，满足结构安全要求。

图3 第1阶模态

图4 第2阶模态

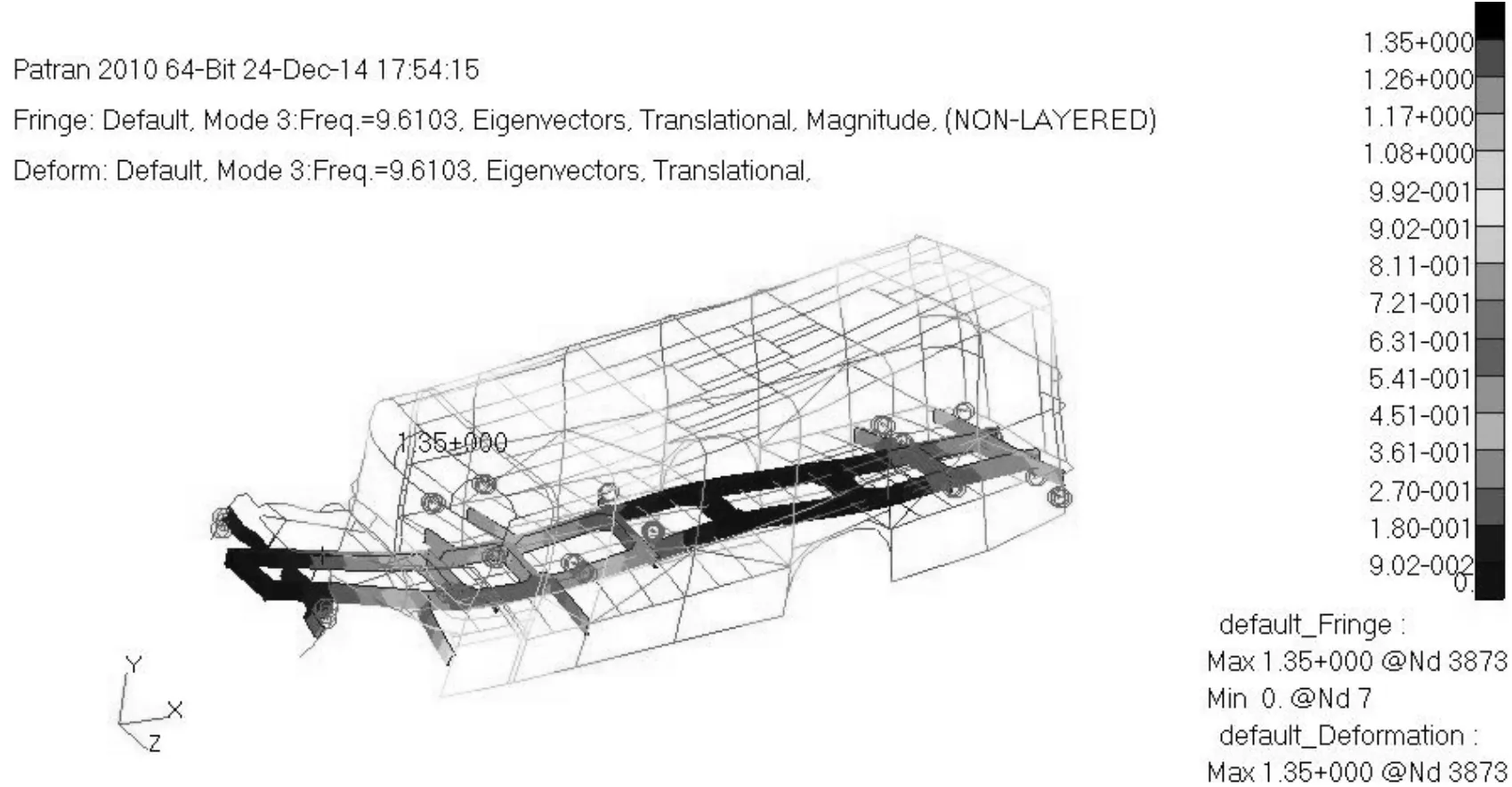
图5 第3阶模态

3.3 车身骨架振动分析和优化

在不同频率下各部分振幅不尽相同，当某几个节点在大多数频率下的振幅都较大时则需对与该节点有联系的骨架部分进行分析，在整个车身设计中全面考虑并加以改进。由各阶振型图可见，校车车身骨架整体各部位振动较为和谐。在部分频率下，振幅大、振型多的现象大多出现在顶棚后侧和后侧围舱门的上横梁上(如图6所示)，而此横梁是固定后舱安全门的主要承载梁，其强度保证了舱门与后围的配合，在此处必须找出加强骨架的方法以保证校车的安全性要求。

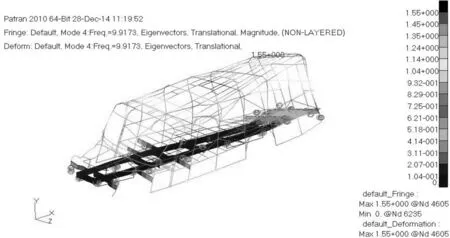
图6 优化前的第4阶模态

为保证顺利装配,后围骨架纵横梁采用规格为30 mm×30 mm×1.5 mm的矩形钢管。由于其本身长度大，在激励作用下振幅明显增大，同时该部位位于车厢后侧舱门上部，故该舱门出于校车安全设计的要求，必须保证一定的尺寸和强度。此外，下方的支撑刚性也比其他横梁差。在这些方面的综合作用下，该处的振幅较其他位置大。对于该处结构的改进，在保证客车装配性要求的提下，可以通过增加横梁的载面尺寸或壁厚解决。截面尺寸可更改为40 mm×40 mm×1.5 mm，或者型材壁厚可增加为2 mm，由此提高抗弯载面模量。还可通过在该横梁与安全门两侧纵梁之间增加短横梁以提高该处刚性和弯曲动载荷，有效减小振幅。为减少工作量和降低成本，本文采用增加短横梁的方法。优化后再次进行模态分析得到第4阶模态振型，如图7所示，可见后围薄弱部位振幅明显降低，确保了骨架的承载安全。

图7 优化后的第4阶模态

4 结束语

本文首先使用Proe对某品牌校车进行三维实体建模，然后利用Patran对其车身骨架进行了有限元建模，而后使用MSC.Nastran对车身骨架进行了无约束无载荷的自由模态分析。通过分析计算得到了车身骨架的固有频率和振型。提取了前10阶模态进行分析，并对该骨架的动态性能进行了评价。对薄弱区域提出相应的优化措施。模态分析结果可为车身进一步动力学分析和设计优化提供参考。

[1] 余志生.汽车理论[M].北京:机械工业出版社,2000.

[2] 季文美,方同,陈松淇.机械振动[M].北京:科学出版社,1985.

[3] 秦民， 蒋永峰， 马天飞，等. 悬架液压衬套液固耦合有限元分析[J]. 重庆理工大学学报:自然科学版，2014(7)：5-10.

[4] 王若平， 柳淑云， 朱国梅. 大客车车身骨架早期局部开裂分析[J]. 重庆理工大学学报:自然科学版， 2014,28(11):1-5.

[5] 傅志方.振动模态分析与参数识别[M].北京:机械工业出版社,1990.

[6] 傅志方,华宏星.模态理论分析与应用[M].上海:上海交通大学出版社,2000.

[7] 李军.精通PRO/ENGINEER中文野火版-零件设计篇[M].北京:中国青年出版社,2004.

[8] 于开平,周传月,谭惠丰,等.Hypermesh从入门到精通[M].北京:科学出版社,2005.

[9] 机械工程材料性能数据手册编委会.机械工程材料性能数据手册[M].北京:机械工业出版社,1994.

[10]张晶，张瑞乾.某微型客车车身模态分析[J].机械制造与制动化，2012,41(6):100-102.

[11]沈浩，陈昌明，雷雨成.客车车身模态分析及评价[J].公路交通科技,2003,20(2):128-130.

[12]王涛.客车车身动态特性研究[D].合肥：合肥工业大学,2011.

[13]曹树谦，张文德，萧龙翔.振动结构模态分析理论、分析与应用[M]. 天津：天津大学出版社，2001.

[14]张准，汪凤权.振动分析[M].南京：东南大学出版社,1991.

[15]Beermann H J. Static analysis of commercial vehicle frames:a hybrid finite element and analytical method [J].Int.J.of Vehicle Design， 1984,5(1):25-26.

(责任编辑 刘 舸)

Modal Analysis of a Bus Body Structure Based on MSC.Nastran

WANG Ruo-ping, LIU Sheng-zhong

(School of Automotive and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)

The finite element modeling for auto- body structure was carried out with the help of pre and post processing software for finite element-Patran. The solution of modal analysis to the model in undamped free vibration was performed with MSC.Nastran and the post processing analysis of the calculated result was carried out with Hypermesh. Based on the finite element analysis of school bus’ body structure, a comprehensive evaluation and improvement for the design of the car body frame was provided.

school bus; auto-body; model analysis; MSC.Nastran

2014-12-06 作者简介：王若平(1960—)，女，黑龙江哈尔滨人，博士，教授，主要从事汽车理论设计与方法研究；通讯作者 刘圣仲(1990—)，男，江苏人，硕士研究生，主要从事车辆安全研究。

王若平，刘圣仲.基于MSC.Nastran的某校车车身结构的模态分析[J].重庆理工大学学报：自然科学版，2015(3):5-9.

format：WANG Ruo-ping，LIU Sheng-zhong.Modal Analysis of a Bus Body Structure Based on MSC.Nastran[J].Journal of Chongqing University of Technology:Natural Science,2015(3):5-9.

10.3969/j.issn.1674-8425(z).2015.03.002

U463

A

1674-8425(2015)03-0005-05