房地产价格评估方法前沿动态及其应用研究

姜松

(重庆理工大学经济与贸易学院，重庆 400054)

房地产价格评估方法前沿动态及其应用研究

姜松

(重庆理工大学经济与贸易学院，重庆 400054)

房地产评估活动是市场主体决策与交易行为达成的重要环节，正确有效的评估活动基于并依赖于科学合理的评估方法的运用。在系统梳理了房地产评估中的各类方法后，在比较和剖析传统评估方法局限性的基础上，对人工神经网络法、特征价格法、空间分析法、模糊逻辑法及自回归单整移动平均法(ARIMA)等前沿评估方法及其原理进行介绍，并通过相关案例引用及实证分析揭示其应用性，力争为客观评价房地产价格提供有效评估工具和奠定坚实理论基础。

房地产;价格评估;人工神经网络法;特征价格法;空间分析法;模糊逻辑法;自回归单整移动平均法

Key words:real estate;price evaluation;artificial neural network method;hedonic price method; spatial analysis;fuzzy logic method;Autoregressive Integrated Moving Average

一、引言

伴随着我国经济体制转轨与市场化进程推进，住房分配制度改革也早已迈入市场化轨道，房地产业日益成为国民经济社会发展的重要产业，对国民经济社会发展做出了重要贡献。房地产业的稳定与健康发展关乎城镇化建设推进、人民生活水平提高乃至经济社会的稳定运行。但与此同时，房地产属性的特殊性也决定其不仅是日常生活的必需品，更是市场主体推崇的重要投资品，房地产投资一直是本土投资者和外籍投资者的重要选择。据统计资料显示，1980年我国房地产业全社会固定资产投资总额为101亿元，而到2012年增长至99 159．31亿元，年均增速达24．02%。国外投资者中，1997年我国房地产业FDI总额为62．22亿美元，到2010年达到239．86亿美元，年均增长10．93%，且还有进一步上升的趋势。在内外空前的投资“热潮”中，如何正确把握与判断房地产价格及其动态走势，就成为诸多投资活动的关键环节和市场主体决策的重要指引。

作为理性“经济人”的市场主体，其做出理性投资决策的首要步骤就是要实施房地产评估，并通过评估确定房地产价值及其“外化”表现形式——价格。随着城镇化进程加快，房地产供需不平衡与偏差的现象十分明显，不但加剧了宏观经济运行的不稳定性和风险，也给评估活动造成诸多不便，尤其是在贫富差距、城乡差距和区域差距拉大的现实背景下，属性的异质性也使房地产价格的形成机制同一般商品相比存在显著不同:在房地产市场竞争“非充分性”、类别异质性的条件牵制下，房地产市场无法依靠供需均衡机制形成“均衡价格”。因此，必须实施房地产价格评估以促使其价值回归和形成合理的均衡价格。从这个层面来讲，随着市场经济阶段演进、经济转型、体制转轨和创新驱动，开展房地产评估具有重要的理论意义与现实意义。

一般而言，房地产评估活动主要由房地产中介机构、房地产审计机构、房地产开发商及投资者、房地产经纪人及评估师、贷款人及担保人、基金经理、市场研究人员、购物中心业主及经营者和其他咨询机构等市场主体执行和实施。对房地产价值进行评估的关键是对房地产权责的定量测度(Pagourtzi和Assimakopoulos等)［1］。有效、恰当的定量测度需要依赖科学合理、客观公正的评估方法和技术手段，这直接关系到房地产评估活动的进度与成败，是关键的关键。鉴于此，本文系统梳理了房地产价格评估中的各类方法，通过比较与剖析，揭示传统评估方法的局限性，然后从预测策略的角度梳理了房地产价格评估前沿方法并就其运用特征做了简要介绍，为客观、公正地评估房地产价格奠定坚实的理论基础，也为后续深化研究提供参考与借鉴。

二、房地产价格评估的传统方法梳理及比较

对任何房地产价值评估活动而言，评估活动的最终目的是要对房地产价格做出精准、确切的估计，以反映不同类型特征、不同区域及不同市场中的房地产价格的差异。这同时也说明在评估活动中评估方法的选择不但要满足价值评估的需要，还要反映国家和地区的市场文化和基础条件。从这个层面讲，实施价值评估模型及方法实质上代表着一种市场基本因素。然而，在现实发展中各个国家或地区资源条件、禀赋特征、文化氛围、发展实践乃至所处经济社会阶段是千差万别的，这也直接对房地产价格评估方法的适用性和实用性提出了诸多挑战。评估方法能否反映各个国家或地区的基础条件就成为检验方法成效与质量的“试金石”。通过对已有研究的梳理发现，传统评估方法大多依赖于某种形式上的比较，或通过一系列观测值形成回归方程，主要包括市场比较法、资本金化法、假设开发法与成本法、多元回归与逐步回归法等。

(一)传统房地产价格评估方法梳理

1．市场比较法

市场比较法是房地产价格评估中被广泛运用且操作十分便利的一种评估方法。运用市场比较法实施房地产价格评估，通常需要假定被评估对象价格和市场中同类房地产交易价格相似。因此，实践中运用市场比较法评估房地产价格时，房地产评估主体只需要选择同类市场中若干房地产作为参照，然后按照“效用最大化”原则进行比较与选择，就可以完成价格评估活动。从中亦可以看出，其操作原理十分简单。但是，任何房地产的属性都是不同的，评估者在评估实践中仍需要对评估对象的销售价格进行调整，并以此来揭示不同属性房地产价格受面积大小、建筑质量、销售日期、周边环境等因素影响所产生的差异。总体而言，运用市场比较法评估房地产价格时一般遵循以下几个步骤:首先是寻找具有可比性的房地产，一般可以通过计算评估对象和参考系间的“距离”来确定。评估活动中运用较多的是选择McCluskey等所确定的距离权重［2］，其一般计算公式如式(1)。

式(1)中，λ为闵可夫斯基λ指数，Ai表示第i种因素的权重，Xi表示待售房产的第i种因素价值，Xsi表示参考目标的第i种因素的价值，Aj表示第j种因素的权重，Xj表示待售房产的第j种因素的价值，Xsj表示参考目标的第j种因素的价值。δ(a，b)表示逆三角函数，当a=b时，δ(a，b)=0，当a≠δb时，δ(a，b)=1。其次是调整参考系的销售价格以更好地匹配评估对象。一般而言可以通过加权的方式来调整参考系的销售价格，具体公式如式(2)。

ASPi表示目标参考系的调整销售价格，SPi表示销售价格，Di表示距离，D表示最大距离。第三是运用更多估计值以更为精确和最大限度地反映和逼近市场价值，并以此为基础撰写评估报告。

2．资本金化法

比较简单的房地产评估活动通过运用市场比较法或权重加权就可以完成，但当一个区域的房地产市场高度细分和相似度较高时，市场比较法就缺乏比较的“土壤”，资本金化法正是基于实践中市场比较法的不足而产生的。所谓的资本金化法又称收益还原法，指运用相应技术手段和方法将房地产的未来收益折算成现值，并以此确定评估对象的价格。资本金化法是建立在“预期理论”基石上的。基于预期理论和从房地产购置人的角度来讲，购买房地产所支付的代价应低于房地产未来收益的现值，那么各个时期收益总和就是房价。为此，运用资本金化法来评估房地产价格基本上遵循以下两个步骤:一是计算并确定房地产未来纯收益;二是确定合理的贴现率并将房地产未来收益还原至现在的“现值”，并将各时期收益加总，就可以确定房地产的估计值。具体计算公式如式(3)。

式(3)中，Rt表示未来纯收益，r表示贴现率，t表示时间期限。由式(3)中我们也可以看到，资本金化法下房地产价格评估受房地产未来纯收益、贴现率以及时间期限等三重因素影响与制约，未来纯收益不同、贴现率不同和时间期限不同，房地产价格评估值也就会不同。因而，运用资本金化法的重点与难点也来源于以上三点:受房地产市场变化及市场主体预期调整的影响，房地产未来收益及其增长率亦不是固定不变的。在房地产市场较为繁荣时，房地产市场主体预期普遍趋好，对房地产纯收益的估计也会较高;当房地产市场处于周期性调整或者衰退期时，市场主体预期也会普遍看衰，对房地产纯收益的估计也会较低。此外，随着我国利率市场化进程的推进，贴现率或者还原利率的波动性亦会较为频繁，也为房地产评估带来诸多挑战。

3．假设开发法与成本法

假设开发法也是实施房地产价格评估常用的方法之一，尤其是在房地产项目可行性论证中运用十分广泛，是确定房地产项目推进与否的重要依据。运用假设开发法评估房地产价格基本上要遵循以下几个步骤:首先估计出被评估对象的销售价格，然后在此基础上扣除正常开发成本，剩下的就是评估对象价格;其次根据评估价格确定房地产项目能否推进。所以，假设开发法通常用于做房地产项目的可行性分析。从中可以看出，如何梳理出房地产的开发成本就成为评估活动实施的关键环节。一般而言，房地产开发成本主要包括土地开发费用、设计费用、销售费用、建筑费用、税费、地价和预计利润等。成本法与假设开发法存在相同之处。运用成本法对房地产价格进行评估时，主要是通过将各类建造成本和税费加总以确定房地产的价格。运用成本法实施房地产价格评估易于操作、程序简单，尤其是在房地产市场发展比较滞后、无法通过比较法实施房地产价格评估的时候，成本法更表现出明显的便利性与可操作性。但在现实操作中，尤其是在实施项目可行性评估时，由于受各类商业性因素制约，这种方法的应用并不普遍。

4．多元回归与逐步回归法

多元回归方法也是房地产价格评估与预测中的常用方法。一般而言，运用多元回归方法进行房地产价格评估时，首先要梳理和分析出房地产销售价格的影响因素，并建立计量模型，如式(4)。

其中，Yi表示区域i的房地产销售价格，X1，i表示区域i的房地产估价，X2，i…Xk，i表示其他一系列房地产销售价格的影响因素和变量，μI为随机误差项。多元回归要求变量X1，i，X2，i，…，Xk，i等与随机误差项μI不存在相关性。μI间不存在自相关性，且更为重要的是μI必须服从正态分布特征［3］。但在现实生活中，各要素存在相互联系、相互牵制的关系，要达到这样的假设条件是非常困难的。且受统计数据及其口径制约，许多房地产价格的影响因素无法实现量化，这也成为多元回归中亟待解决的问题。当然，现实中为了增强多元回归方法的有效性和效率，通常运用逐步回归方法对相关变量及影响因素进行逐步回归以筛选出更为精准的模型。通过对拟合系数R2的判断，就可以明晰房地产估价对销售价格的解释程度。

(二)传统房地产价格评估方法评析

总体而言，市场比较法、资本金化法、假设开发法与成本法、多元回归与逐步回归法等传统方法在房地产价格评估中都发挥了重要作用，在房地产评估实践中得到了广泛运用。但通过剖析其方法流程我们也发现，已有研究方法的局限性也为房地产评估工作和评估结果的准确性、科学性和可信性带来了诸多挑战。通过比较发现，传统方法均存在以下共性特征与不足。

1．已有评估方法都存在一定的主观性特征

房地产评估的目的是准确、客观、公正地反映房地产价格及其内在价值，为市场主体实施市场经济活动提供可资借鉴的理论依据与支撑。但通过方法梳理我们却发现，已有方法在房地产价格和价值评估中均存在诸多主观性因素，使评估结果在某种程度上可能会存在“失真”现象。具体而言，市场比较法需要选取目标区域房地产价格为参考基准，并根据一定权重系数对参考系价格进行调整以适应评估对象的要求，但学术界对权重系数的确定并没有形成统一认知，在实践操作中也往往根据操作经验进行主观赋权。资本金化法所依托的是“预期理论”，这就使得评估主体对房地产价格进行评估时的主观性表现更为明显，尤其是当房地产市场处于“繁荣期”时，市场主体预期往往比较高，而处于周期性调整时，市场主体预期会较低，市场主体预期不同会使评估结果发生偏差。假设开发法与成本法中对于建造成本的确定也往往会受到诸多主观因素影响，如房地产开发商为了保守商业机密，对于建造成本往往存在隐瞒现象，主观随意性非常大。此外，运用多元回归与逐步回归法评估房地产价格时在影响因素确定和选择方面受研究局限，存在一定主观性。

2．已有评估方法均对房地产市场及其稳定性有较高要求

现有房地产评估方法基本上均假定房地产市场是稳定的，但受我国经济社会体制转轨、宏观政策波动及居民生活需求异质性影响，房地产市场的波动性特征十分明显，也会使传统评估方法得到的评估结果陷入“失真”困境。具体而言，运用市场比较法实施房地产价格评估时要求目标参考区域的房地产市场非常发达，才能获取尽可能多的参考数据，但如果目标区域房地产市场起步较晚、市场发育滞后，则意味着房地产交易数量较少，比较也就无从谈起。由此可见，市场比较法对房地产市场的发育程度要求是比较高的。更为重要的是，运用市场比较法评估房地产价格时也隐含着房地产稳定的特殊性内涵特质，只有当房地产市场运行稳定时，市场比较法评估出的房地产价格才真实可靠。当房地产市场存在“泡沫”时，运用市场比较法便会形成较大偏差。但就中国现实而言，随着社会资本及大量热钱流入，房地产行业在短时间内过度膨胀，加剧了房地产“泡沫化”［4-6］。在这样的现实条件下运用市场比较法评估我国房地产价格则显得不合适。而资本金化法评估房地产价格时也对房地产市场稳定性有严格要求，尤其是纯收益的确定会因房地产市场繁荣和衰退产生截然不同的结果，影响到房地产价格的最终评定。当房地产市场繁荣时，房地产市场主体预期纯收益一般较高，而当房地产市场衰退时，纯收益预期一般也会较低。此外，贴现率确定也对房地产市场稳定性有严格要求，因为如果房地产市场不稳定，贴现率就无法很好确定。

3．已有评估方法均对样本容量有严格的要求

通过比较还发现，已有评估方法均对样本容量有较高要求。具体而言，运用市场比较法实施房地产价格评估的时候，一般要求评估者首先要选择目标区域大量最近交易的同类房地产价格作比较，因此，目标区域房地产数量和样本容量直接决定着评估结果的准确性。资本金化法也是以市场比较法为基础的，同样对样本容量存在限制。多元回归与逐步回归法更是对样本容量有更高的要求，如果样本容量不足，回归结果会受到直接影响。但从现实情况来看，我国房地产市场化改革起步较晚，数据年限跨期、结构类型等无法满足大数据条件下对样本容量的严格要求，这直接影响了房地产市场评估结果的有效性和科学性。探寻房地产价格评估的新方法、新工具成为新时期亟待解决的问题。

三、房地产价格评估前沿方法及其应用

相较于传统方法，新方法试图通过模仿房地产市场主体的思维过程实现房地产价格评估。这些方法有助于克服传统方法所存在的缺陷，相对于传统方法而言更能体现“定量性”，是房地产评估方法的前沿体现。经过对学术界已有研究成果梳理发现，前沿房地产评估方法主要包括人工神经网络法、特征价格法、空间分析法、模糊逻辑法、自回归单整移动平均法(ARIMA)等，下面先分别介绍各方法的原理，然后通过已有案例实证分析其实际应用性，为后续研究提供可兹借鉴的工具。

1．人工神经网络法

人工神经网络是以人脑为研究对象，通过模拟人脑作用机制实现某些特定目标的非线性信息处理系统。由于人工神经网络法建立在模拟人脑的基础上，所以也被认为是最成熟、最复杂和最完美的信息处理系统。研究伊始，人工神经网络模型被广泛运用于自动化控制、智能识别与图像处理等方面，但近几年来随着人工神经网络模型技术的普及与推广，人工神经网络模型也被广泛引入到经济与管理领域，运用其对房地产价格进行评估就是其中一个重要方面。在现实生活中经验丰富的估价师利用存储在大脑之中的可比实例资料，通过比较实例和估价对象，最终得到估计对象价格［7］。运用人工神经网络模型实施房地产价格评估可以有效克服和避免传统方法中因评估者主观判断而对评估结果产生的不良影响，评估结果的实用性、适用性更强。此外，该模型亦可以有效克服样本容量限制，因为人工神经网络模型是稳定的，所以通过网络学习能力与训练水平提高形成的学习网络存在稳定性，不会随着样本容量扩容而产生变化，研究精度大幅度提高。

在具体应用方面，人工神经网络模型一般涵盖输入层、隐含层和输出层等3部分。其中，输入层主要由房地产价格的各类影响因素组成，用向量表示即为:X→=(x1，x2，…，xn)。隐含层部分主要用来提高网络训练精度，由加权函数和转换函数两部分组成，这两种函数均涉及输入变量和输出变量。其中加权函数通常用于前馈和BP神经网络模型中，可以将其用函数形式表示为:

其中，Xi表示输入变量，Wij表示为隐含层分配的输入值。如李刚分别从交通条件、生活服务设施、教育配套设施、区域环境因素、所在位置、建筑结构类型、建筑面积等诸多方面设置输入变量及其输入值［7］(见表1)。

表1 输入变量及其赋值

转换函数主要用于将可能无限域的输入变换成指定的有限范围内的输出。转换函数类型多样，主要包括线性函数、线性阈值函数、逐步线性函数、Sigmoid函数和高斯函数等。但学术界运用较为普遍的仍然是Sigmoid函数，因为非线性、连续性、单调性和连续可微等原因［8-9］，Sigmoid函数是最优的，见式:输出层主要指房地产销售价格。设置好输入变量、输出变量等后，通过运用Matlab编程就可以求解出人工神经网络模型下的房地产价格评估结果，见表2。由结果中的绝对误差和相对误差比较可知，人工神经网络方法评估房地产价格的误差相对较小，充分说明其在评估房地产价格时具有优越性，评估结果也较为公正和客观。

表2 人工神经网络评估结果

2．特征价格法

特征价格法(Hedonic Pricing Models)是基于房地产特征不同，房地产价格形成机制也会存在差异的原理。特征价格法有时候也被称为效用法或价格法。在房地产评估活动中如果能将不同房地产价格影响因素实施分解并将房地产特征固定不变，就可以将房地产价格变动的特征因素分离出来，剩下的部分就是受供需关系决定的房地产价格变化。传统特征价格法主要用于揭示空气质量、机场噪音、区位条件、邻里环境和物理属性等不可观测变量的效应［10］。通过上述分析与比对可知，已有房地产评估方法基本上都是从整体层面实施房地产评估，“结构”层面的关注相对较少。特征价格法则正好填补了方法论空白。因而相比较已有评估方法，特征价格法取样相对容易、模型的经济意义更为直观。特征价格法也被学术界赋予崇高地位，被认为是最有运用前景的方法。就现阶段而言，特征价格模型主要包括3种类型函数，线性函数:lnPi=α+∑βiXi+υ，对数函数:lnPi=α+∑βilnXi+υ，半对数函数:Pi=α+∑βiXi+υ。其中，Pi为房地产销售价格，βi为特征变量的特征价格，Xi表示特征因素。

由于特征价格法所涉及的特征变量一般都是与房地产属性紧密相关、高度关联的属性变量，因而在实际操作中运用特征价格法评估房地产价格时，要对其属性做细致入微的调研，这就使得基于宏观层面的统计分析变得十分艰难。因此，现阶段特征价格法的操作基本上都是基于调研数据。贾士军、蔡砥基于广州房地产二手交易市场的月度调研数据并结合GIS(地理信息系统)技术，从距离商业中心距离、山江公园距离、地铁距离、噪音、间隔、是否装修、装修新旧度、朝向、景观、楼层、楼龄、阳台数量等特征变量层面，实施房地产价格评估，其评估结果如表3所示［11］，可看出特征变量的变化对房地产销售价格的影响。因而，相比较传统方法，特征价格法评估房地产价格时对房地产市场发育程度也有严格要求，对信息透明度、公开程度的要求极高，这样所得到的评估结果才更具信度和科学性。

表3 特征价格法评估结果［11］

3．空间分析法

GIS的发展不但为定位和变量的量化提供了便利性，也改变了传统的对于距离测量仅仅依靠欧氏距离(Euclidean distance)进行量化的局限性。随着空间计量与统计方法的整合，它们的分析能力也更强［12-16］，空间格局分析、空间自回归分析［17-20］以及变异分析和克里格技术［21-22］等方法还有助于探测邻近区域的影响和揭示房地产市场的变异性，而这是传统计量方法所不能揭示的。传统计量经济学极大地忽视了地区数据模型存在的空间异质性和观测中存在的空间依赖性两大问题，违反了回归模型的Gauss-Markov假设［23］。空间计量经济学是基于对空间结构的规范描述，关于模型设定、估计、假设检验以及预测的计量经济学方法［24］，很好地解决了传统经济学中忽视的两大问题。运用空间方法来评估房地产价格的主要步骤和多元回归与逐步回归法存在相同之处，唯一不同的是在空间计量模型中，引入空间权重矩阵Wij，其为N×N向量。就目前而言，空间计量模型包括多种形式，将其写成一般形式主要如式(5)。式(5)中，如果θ=0，模型转变为带自动干扰项的空间自回归模型;当λ=0，模型转变为空间杜宾模型;当θ=0和λ=0时，模型为空间自回归模型;当θ=0和ρ=0时，模型为空间误差模型;当θ=0，ρ=0和时，模型即变为空间计量一般模型。

模型中，Y为房地产销售价格，X指涵盖房地产估价在内的房地产销售价格影响因素，通过拟合程度就可以确定房地产估价对销售价格的揭示程度，这一点同多元回归与逐步回归法是相似的。为了进一步说明空间分析法在房地产价格评估上的适用性，文章进一步通过数据对模型进行估计验证。因为空间分析方法是将空间的相互影响因素融入分析模型，所以在具体运用时一般适用于面板数据。为此，运用1999—2010年中国28个省份(不包括西藏、甘肃、新疆)的面板数据评估房地产价格。同时，基于统计数据获取的便利性，选取土地供应、基础设施条件两个变量作为影响房地产销售价格的变量。表4分别给出了SAR模型(空间自回归模型)、SDM模型(空间杜宾模型)、SAC模型(空间自相关模型)的估计结果。从结果可知，引入空间变量后，各模型的拟合程度较好，可以用其进行房地产价格评估。

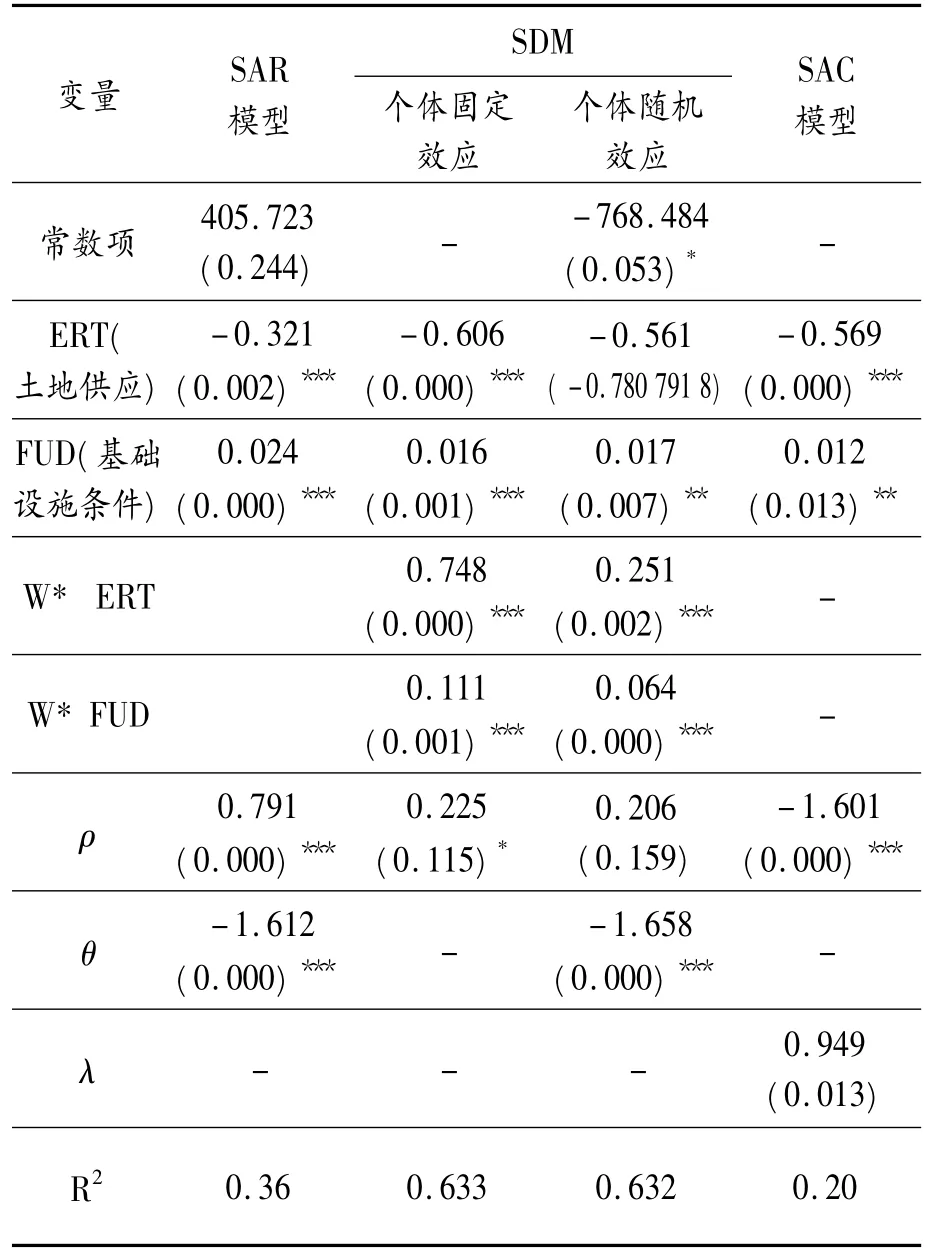
表4 房地产价格评估的空间计量估计

4．模糊逻辑法

模糊逻辑法最早是由Zadeh在关于计算机程序改进的“模糊集合”理论中提出的［25］。经典布尔逻辑是“二维”的，也就是说计算机只能对0和1、是与否等这样的二元逻辑进行识别与判断，而对于一些模糊概念的判断则显得无能为力，计算机在某些“灰色地带”及信息有限条件下无法完成处理能力，而这也是二元逻辑的局限性。模糊逻辑法就是在这样的历史条件下诞生和发展的。模糊逻辑法起初是在计算机领域应用较为广泛，但随着方法的不断完善，它逐渐向经济、社会各个研究领域蔓延，房地产价格评估领域就是其应用的一个重要方面。通过分析发现传统评估方法都无法避免不确定性因素的干扰。在传统房地产价格评估方法中，如运用市场比较法对房地产价格进行评估的时候，就无法刻画评估对象和参考系间的差异性，在计算出修正价格后仍无法客观准确地确定评估对象的价格。同时，通过传统方法比较我们也发现，如何准确反映房地产价格的影响因素在房地产价格评估中占据非常重要的地位，但受诸多因素干扰，现实中有些因素是无法进行量化的，成为研究开展和实施过程中亟待解决的问题。

模糊逻辑法为这类问题提供了一个可供参考的解决思路。模糊逻辑法通过运用专家打分法对评估对象和参考系价格的影响因素进行综合测评与量化，得到评估对象和参考系的综合得分，然后通过“直线内插法”就可以得到房地产评估价格。从中也可以看出，模糊逻辑法可以将以前方法中无法量化的影响因素进行量化处理，不但增强了评估结果可信度、科学性，也有效拓展和延伸了指标体系。模糊逻辑法弥补了已有方法的不足，为无法量化的因素提供了一个可资解决与量化的思路。但模糊逻辑法也不是万能的，也存在一定主观性，尤其是在专家打分部分容易受到专家偏好、主攻领域等主观因素影响，给评估结果的客观性造成一定影响。

5．自回归单整移动平均法(ARIMA)

上述房地产价格评估方法中，基本上都是多变量模型的，单纯依靠房地产价格变动规律对其进行评估的方法还并不多见。随着统计数据，尤其是月度和季度数据的获取更为便捷，使得通过房地产价格变动规律评估房地产价格成为现实。这类方法在计量经济学中属于动态计量经济学的范畴，通常运用时间序列的过去值、当期值和滞后扰动项的加权和建立模型来“解释”时间序列的变化规律［26］。关于时间序列的模型大致可以分为平稳时间序列模型和非平稳时间序列模型两类。其中，平稳时间序列模型主要有自回归AR(p)模型、移动平均MA(q)模型以及ARMA(p，q)模型。在模型ARMA(p，q)中，p为自回归项数，q为移动平均项数。但现实中的经济社会是复合演进的系统，任何经济现象都存在非平稳的特质，房地产价格也会随着时间的变化而变化，在各个时间点上的随机规律也不同。因此，很难通过已知的信息去预测序列未来的演进趋势。为此，BOX-Jenkins提出了适应非平稳序列的ARIMA(p，d，q)模型，其所对应的形式为:Φ(L)(1-L)dPt=c+Θ(L)μt。其中，Φ(L)=1-φ1L-φ2L2-… -φpLP，Θ(L)=1+φ1L+φqL2+…+φqLq，d为时间序列成为平稳时所做的差分次数，ARIMA(p，d，q)模型是基于时间序列数据进行经济预测的重要方法［27-29］，是实施房地产价格评估活动中唯一依赖单变量时间序列的方法。

运用移动平均法进行评估时，到底是选用ARMA(p，q)模型还是选用ARIMA(p，q，d)模型呢?这就要取决于所运用数据的平稳性，这也是进行房地产价格评估的关键步骤。接下来以自回归移动平均方法对1995—2013年我国住宅房屋平均销售价格进行评估。一是对房地产价格数据进行平稳性检验，运用的方法是ADF和PP检验。平稳性检验结果见表5。在ADF和PP检验中，房地产价格P为非平稳时间序列。为此，采用差分法对其房地产价格P进行差分变换，通过差分变换的差分序列ΔP为平稳的时间序列，为一阶差分过程。

表5 数据平稳性检验

为此，应选用ARIMA(p，d，q)模型，而且其具体形式是ARIMA(2，1，2)。用E-Views软件以及最小二乘法OLS对模型进行估计。估计结果如表6。

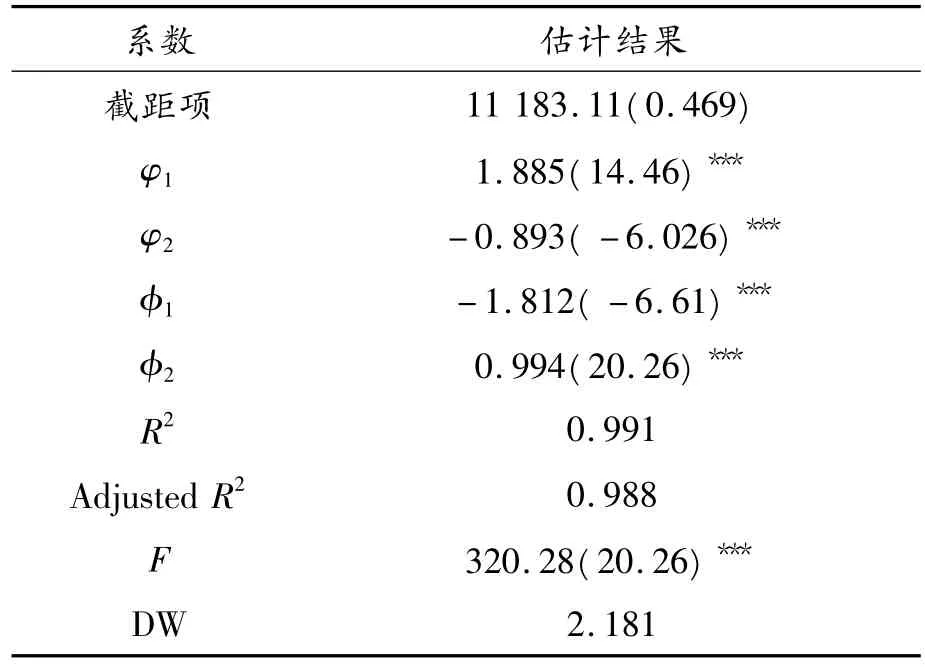
表6 ARIMA(2，1，2)模型估计结果

结果可知，调整后的R2为0．988，说明模型拟合程度非常好，可以用其来对房地产价格进行评估。相比较其他几种方法，自回归单整移动平均法是基于统计数据进行建模的，数据获取成本同其他几种方法相比，成本更低、效率更高，为房地产价格评估方法的拓展提供了可资借鉴的重要手段，随着房地产市场发育渐趋成熟，自回归单整移动平均法因为其自身操作的便利性，应用前景也会十分广泛。

四、结语与讨论

任何评估方法都是建立在一定假设条件基础上的，根植于特定的市场环境和文化氛围，当假设条件和环境发生相应变化后，评估方法的效力与精准性也会发生相应变化，给评估结果造成不良的影响，无法反映房地产的真实价值。通过对现有评估方法的反思与梳理，可以从本质上解构已有方法中存在的缺陷与不足，为房地产价格评估奠定坚实理论基础和提供可靠技术手段。本文在梳理传统房地产评估方法的基础上，通过比较揭示了已有房地产评估方法中存在的缺陷与不足。然后，从方法创新与演进的视角梳理了前沿房地产评估方法及其原理，并通过相关案例与相关数据进行实证分析，以揭示新兴方法的适用性与应用性。一方面，前沿房地产评估方法是在传统方法的基础上发展起来的，是对传统方法存在局限性和不足的有效弥补，为房地产评估工作提供了有效、可靠和科学的技术手段。但另一方面，前沿房地产评估方法的发展也并不代表对传统方法的彻底摒弃，在房地产市场发展相对滞后、基础条件不成熟的情境下，传统方法在现今和未来很长一段时间内仍会占据重要地位，发挥重要作用。随着房地产市场发育渐趋成熟、数据获取更为便捷，前沿评估方法的重要性会逐步凸显，应用前景会更加广泛，成为房地产评估的可靠手段和工具。

［1］PAGOURTZI E，ASSIMAKOPOULOS V，HATZICHRISTOS T，et al．Real estate appraisal:a review of valuation methods［J］．Journal of Property Investment＆Finance，2003，21(4):383-401．

［2］MC-CLUSKEY T L，PORTEOUS J M．Engineering and compiling planning domain models to promote validity and efficiency［J］．Artificial Intelligence，1997，95(1):1 -65．

［3］MAKRIDAKIS S，WHEELWRIGHT S C，MCGEE V．Forecasting，methods and applications［M］//Wiley series in management．John Wiley，1983．

［4］辜胜阻，刘江日．城镇化要从“要素驱动”走向“创新驱动”［J］．人口研究，2012(6):3-12．

［5］徐忠，张雪春，邹传伟．房价、通货膨胀与货币政策——基于中国数据的研究［J］．金融研究，2012(6): 1-12．

［6］范允奇，王艺明．中国房价影响因素的区域差异与时序变化研究［J］．贵州财经大学学报，2014(1):62 -67．

［7］李刚．基于人工神经网络的房地产估价研究［D］．西安:长安大学，2006．

［8］BORST D W，TSUKIMURA B，LAUFER H，et al．Regional differences in methyl farnesoate production by the lobster mandibular organ［J］．The Biological Bulletin，1994，186(1):9-16．

［9］TRIPPI R R，TURBAN E．Neural Networks in Finance and Investing:Using artificial intelligence to improve real world performance［M］．McGraw Hill，1992．

［10］JANSEN J C，SHAN Z，MARCHESE L，et al．A new tinplating method for three-dimensional mesopore networks［J］．Chemical Communications，2001(8):713-714．

［11］贾士军，蔡砥．住宅特征价格分析——以广州为例［J］．广州大学学报，2012(7):65-68．

［12］ANSELIN L，GETIS A．Spatial statistical analysis and geographic information systems［J］．The Annals of Regional Science，1992，26(1):19-33．

［13］GRIFFITH D A，CSILLAG F．Exploring relationships between semi-variogram and spatial autoregressive models［J］．Papers in Regional Science，1993，72(3):283 -295．

［14］ZHANG Z，GRIFFITH D A．Developing user-friendly spatial statistical analysis modules for GIS:An example using ArcView［J］．Computers，environment and urban systems，1997，21(1):5-29．

［15］THERIAULT M，DES R F，VILLENEUVE P，et al．Modelling interactions of location with specific value of housing attributes［J］．Property Management，2003，21(1):25-62．

［16］LEVINE R，ZERVOS S．Stock market development and long-run growth［J］．The World Bank Economic Review，1996，10(2):323-339．

［17］LEGENDRE P．Spatial autocorrelation:trouble or new paradigm?［J］．Ecology，1993，74(6):1659-1673．

［18］CRESSIE N．Statistics for Spatial Data［J］．Terra Nova，1992，4(5):613-617．

［19］ORD J K，GETIS A．Local spatial autocorrelation statistics:distributional issues and an application［J］．Geographical analysis，1995，27(4):286-306．

［20］TIEFELSDORF M，BOOTS B．A note on the extremities of local Moran’s Iis and their impact on global Moran’s I［J］．Geographical Analysis，1997，29(3):248-257．

［21］DUBIN R A．Spatial autocorrelation and neighborhood quality［J］．Regional science and urban economics，1992，22(3):433-452．

［22］PANATIER Y，et al．Software for Spatial Data Analysis［M］．New York:Springer-Verlag，1996．

［23］沈体雁，等．空间计量经济学［M］．北京:北京大学出版社，2010．

［24］ANSELIN L．Spatial econometrics:methods and models［M］．Germany:Springer，1988．

［25］ZADEH L A．Fuzzy algorithms［J］．Information and control，1968，12(2):94-102．

［26］高铁梅．计量经济分析方法与建模［M］．北京:清华大学出版社，2009．

［27］DICKEY D A，FULLER W A．Likelihood ratio statistics for autoregressive time series with a unit root［J］．Econometrica:Journal of the Econometric Society，1981，49 (4):1057-1072．

［28］GRANGER C W J，Newbold P．Spurious regressions in econometrics［J］．Journal of econometrics，1974，2(2):111 -120．

［29］TSE Y，BOOTH G G．Information shares in international oil futures markets［J］．International review of economics＆finance，1997，6(1):49-56．

(责任编辑许若茜)

Research Frontier and Application of Real Estate Appraisal Methods

JIANG Song
(School of Economy＆Trade，Chongqing University of Technology，Chongqing 400054，China)

Real estate assessment activities is an important part of decision-making and trading behavior reached of market players，but the correct and effective assessment activities rely on the use of scientific assessment methods．This paper systematically reviewed the various types of real estate assessment methods in comparison and analysis of the limitations of traditional assessment methods，and introduced the cutting-edge methods，theirs principle and applicability by sitting examples or empirical analysis，such as artificial neural network method，hedonic price method，spatial analysis，fuzzy logic method and Autoregressive Integrated Moving Average(ARIMA)，and strived to provide an effective assessment tools and to lay a solid theoretical foundation for the objectively evaluation of real estate prices．

F293．3

A

1674-8425(2015)11-0047-10

10．3969/j．issn．1674-8425(s)．2015．11．008

2014-12-12

国家社会科学基金项目“全球价值链视角下西部制造业转型升级机制与路径选择研究”(14BJY076);教育部人文社会科学青年基金项目“农业适度规模经营与金融服务共生演化机理及模式研究——基于农业价值链视角”(15XJC790003);重庆市教委科学技术研究项目“农业适度规模经营与金融服务创新的协同演化机制研究——基于价值链视角”(KJ1500919);重庆市社会科学规划青年项目“重庆市农业适度规模经营发展与金融服务创新的协同机制研究——基于价值链视角”(2015QNJJ08);重庆理工大学科研启动基金项目“经济金融化对城镇化演进的影响及其机理研究”(2014ZD40);重庆理工大学研究生教育教学改革项目“全日制专业学位研究生实践教学质量评估机制设计与模式创新研究”(yjg2014208);重庆市研究生教育教学改革研究项目“全日制农业推广硕士培养模式研究”(yjg133051)

姜松(1986—)，男，讲师，博士，研究方向:宏观金融、农村金融、数理金融方法及应用。

姜松．房地产价格评估方法前沿动态及其应用研究［J］．重庆理工大学学报:社会科学，2015(11):47 -56．

format:JIANG Song．Research Frontier and Application of Real Estate Appraisal Methods［J］．Journal of Chongqing University of Technology:Social Science，2015(11):47-56．