考虑时变性影响的盾构壁后注浆浆液固结及消散机制研究

梁 禹，阳军生，王树英，曾学艺

（1.中南大学 土木工程学院，湖南 长沙 410075；2.长沙市城投基础设施建设项目管理有限公司，湖南 长沙 410000）

1 引 言

盾构法因其安全、高效、对周边环境影响较小等特点，目前已在地铁隧道和越江隧道广泛应用。由于盾构壳体内径大于管片衬砌外径，盾尾脱离管片后在管片与地层之间会形成盾尾间隙。为保证工程质量，需从管壁后向该空隙中注入浆液，填充间隙，控制地层应力释放和地层变形。在盾构注浆过程中，应尽量对注浆压力进行精确控制，防止管片局部或整体上浮、错台、开裂、压碎或其他形式的破坏。壁后注浆的扩散、消散机制研究关系到注浆技术能否成功。

近年来，部分学者通过理论分析、数值模拟、模型试验及现场监测等方法对壁后注浆浆液的扩散、浆体压力分布等开展了研究。Lombardi 等[1]建立的注浆理论均未考虑注浆材料黏度时变特性，与注浆实际情况不符，存在一定的局限性；孙子正等[2]通过室内试验探讨了浆液在裂隙注浆中的扩散机制与压力特性；叶飞[3-4]、苟长飞[5]等引入等效孔隙率的概念，假定注浆浆液为黏度时变性流体且浆液沿半球面扩散，得到了浆液扩散半径及对管片产生的压力计算式；白云[6]、李志明[7]等应用流体力学与极限平衡法的基本原理并结合浆液的时变特性，探讨了盾构隧道壁后注浆压力的计算方法和浆液分布；袁小会[8]、刘健[9]等基于宾汉体浆液的时变方程与流体黏度时变性方程，推导了浆液柱-半球形渗透注浆机制；Bezuijen 等[10]对隧道壁后注浆压力进行实时监测指出，浆体压力表现为上小下大的形式，随时间推移浆体压力逐步减小，最终趋向于地下水压力值。

目前大多数研究主要集中在浆液渗透扩散模式及浆液压力分布方面，未考虑浆液消散过程中浆液黏度的时变性，阮文军[11-12]、李术才[13]等揭示了浆液黏度会随时间增长而增加。尤其在渗透系数较大的地层中进行壁后注浆时，浆液黏度时变性会引起地层渗透系数变小，进而对浆液消散及注浆压力分布产生较大影响，这就使得浆液压力计算值可能与实际不符，影响实际注浆压力的确定与精细化控制。

基于广义虎克定律、达西定律和力学平衡原理，推导了渗流阻力作用下浆液固结方程和浆液压力消散方程，并考虑了浆液黏度时变性对周边地层渗透性的影响。以长沙南湖路湘江隧道典型地层为例，分析了浆液固结、消散机制及浆液压力沿管片外壁分布规律，探讨了浆液性质和地质条件对浆液压力消散的影响，为精细化分析施工阶段管片受力提供了计算依据。

2 浆液固结及消散机制

2.1 固结变形原理及方程推导

浆液从注入至凝结硬化的过程中，浆液中的水分向周围地层渗透，浆液受围岩压力作用发生固结变形，浆液压力将会随之消散。韩月旺[14]、张莎莎[15]等利用理论分析和室内试验等手段对注浆体固结变形及浆液压力消散进行了研究，但并未考虑浆液时变性的影响。

隧道管片脱出盾尾后，使周围地层产生了一定的扰动。假定该扰动范围土体为弹性变形，其扰动厚度与盾尾空隙厚度相当。取该范围土体平面内的某微元体为研究对象，微元体长度为盾尾空隙厚度（浆液厚度）δ 与土体扰动圆环厚度r 之和。如图1 所示。

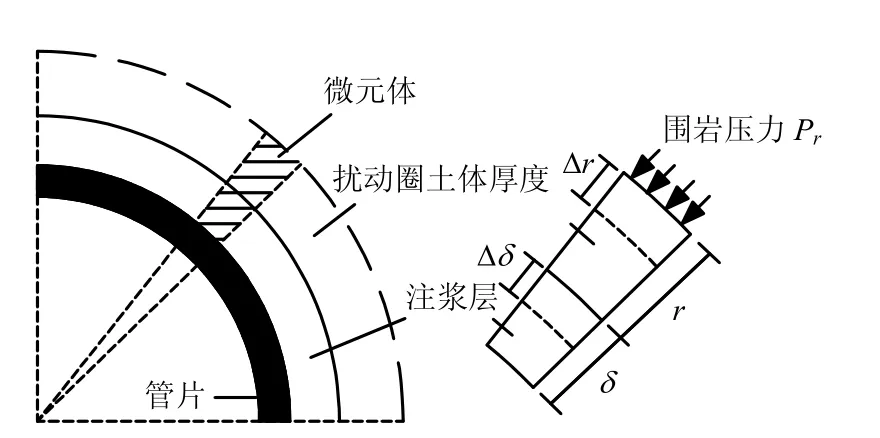
图1 微元体受围岩压力变形示意图Fig.1 Deformation of representative element under surrounding rock stress

周围土体受径向围岩压力作用将发生位移，对于微元体而言，可近似认为只发生径向位移 Δr，不考虑微元体与管片外壁接触效应，即假定浆液与扰动土体具有相同的弹性常数。

由广义虎克定律可得平面应变情况下其径向应变变化量Δεr为

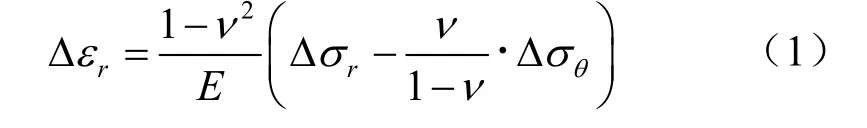
式中：Δσr为微元体径向应力的变化量；Δσθ为微元体切向方向应力变化量。E为土体弹性模量；ν为土体泊松比。由于Δσθ≈ 0，进而可得

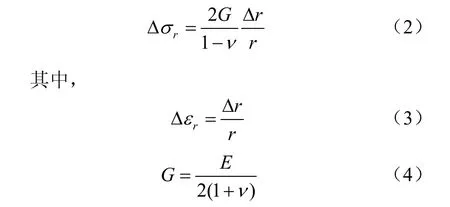
式中：Δr为土体径向变形量；G为土体剪切模量。

浆液与周围地层之间的相互作用方式主要有渗透、压密和劈裂，而浆液固结过程主要发生在浆液渗透阶段。浆液注入盾尾空隙后，浆液压力与周围土层的水土压力不一定完全相等，但在较短的时间内，通过应力的传递以及浆液和土体的协调变形，在浆液与土体接触面上迅速建立起力学平衡，浆液压力与土体中的总应力相等，即

式中：p浆为浆液压力；σ′为地层有效应力；p孔为孔隙水压力。

只要浆液压力大于地层中的孔隙水压力，浆液就会向地层渗透。渗透的驱动力，即渗透压力p 可以表示为

可见，渗透压力p 与地层有效应力σ′相等，当p=0（p浆=p孔）时，渗透过程结束。

固结过程中浆液层厚度减小了 Δδ，隧道半径随之减小了 Δr，引起了周围地层的弹性卸载，土体有效应力相应降低了Δσr，导致了浆液中渗透压的减小，即

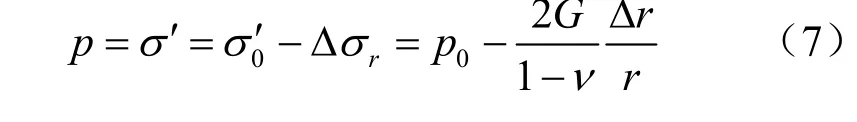
式中：σ0′为初始地层有效应力；p0为初始浆液渗透压。

设浆液的初始孔隙率为ni，浆饼（浆液固结硬化层）的孔隙率为 ne，浆饼的渗透系数为k，时间t 内形成的浆饼厚度为x，t 时浆液压力与地层孔隙水压力的水头高差为 Δh，则单位时间内通过单位面积浆饼的渗流量q为

渗流量q 就是单位时间内浆液中排出的液体的体积。同时，渗流量q 又可看作在浆饼形成过程中，在t 时间内单位时间内浆液固结导致其孔隙体积的变化量，即

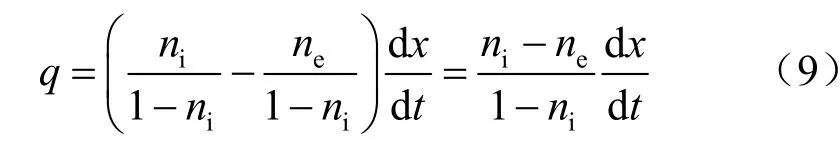
根据式（8）和式（9）可得

同时，根据几何协调条件可知，隧道半径的减小量与浆饼厚度之比应等于浆液固结变形前、后孔隙率的变化量与固体体积率之比，即

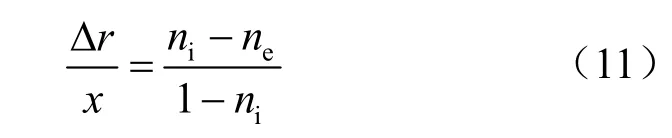
又因水头高度差 Δh 可以表示为

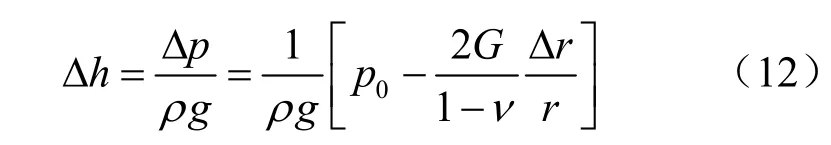
式中：Δp为浆液渗透压的变化量（MPa）；ρ为浆液重度（kN/m3）；g为重力密度（N/kg）。

将式（10）、（11）代入式（12），可得浆液的固结方程为

式中：h0为初始渗透压对应的压力水头高度（m）。

对式（15）进行求导，可得到浆液往周边地层渗透过程中浆体的累积固结厚度。

2.2 地层渗流阻力对浆液压力消散影响

浆液固结变形导致部分浆液从浆体析出并向地层中渗透，在渗透过程中，会遭遇地层渗流阻力。在计算浆液渗透消散作用时不仅应考虑浆体固结（浆液析出）作用，也不能忽略地层渗流阻力的影响。基于上节中的假定条件，根据达西定律可知，浆液单位面积流量q为

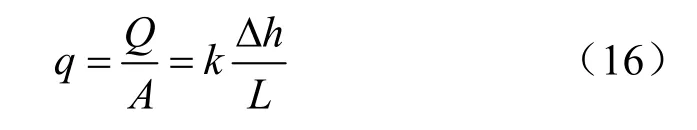
式中：Q为单位时间断面总流量；A为断面面积；L为渗流路径长度。

用渗流时间表征渗流阻力f，则根据式（16）可得

因此，浆液从浆体中析出遇到的渗流阻力 fg可以表示为

浆液渗入地层中遇到的渗流阻力 fs可以表示为

以单位长度隧道为研究对象，单位时间内从浆体中排出的液体流量Q浆为

式中：R为隧道半径。

隧道周围地层中半径r 的圆环处，单位时间内的液体流量Q地为

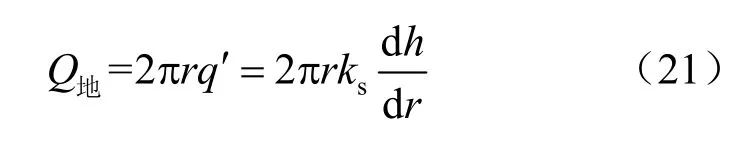
式中：h为半径R 与半径r 处的孔隙水压力水头高差；ks为浆液在地层中的渗透系数。

土体中流动的浆液正是从浆体中析出的，因此，式（20）、（21）表示的流量相等，则有

对上式进行积分，并利用图2 所示的边界条件r=R，h=0；r=H，h=h0，令F=R ln(H/R)，可得

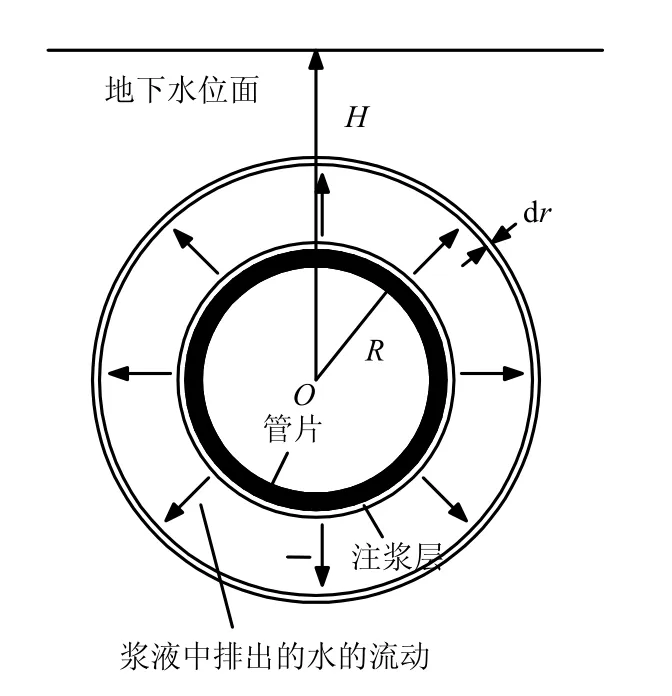
图2 浆液向围岩渗透示意图Fig.2 Grout permeating toward surrounding rock

由式（23）可见，浆液渗流遇到的阻力与土层的渗透系数成反比。根据式（15）的推导过程，可得考虑地层渗流阻力时的浆液固结变形方程为

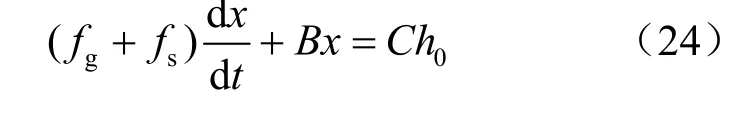
对式（24）进行求导，可得到考虑地层渗流阻力作用下浆液累积固结厚度。

3 地层渗透系数时变性

在式（24）中，未考虑周边地层渗透系数变化对浆液固结和浆液压力消散的影响。同步注浆浆液向周边地层渗透时，浆液逐渐充填地层颗粒间隙，颗粒间的空气和水被挤出。随着浆液逐渐凝结，浆液充填区域的地层渗透系数将逐渐减小（见图3）。若采用固定的初始渗透系数值计算，就使得注浆扩散半径、浆液压力等计算值与实际不符，不仅难以保证注浆效果，还可能造成工程隐患。因此，本文将地层渗透系数的变化考虑至式（24）中去。

图3 浆液扩散使围岩渗透系数改变Fig.3 Rock permeability change due to grout diffusion

盾构壁后注浆所用浆液一般为水泥基浆液，在注浆过程中流型不变，其黏度与切变运动时间有关。注浆时，浆液的黏度随时间发生变化。t 时刻黏度μ(t)可用指数函数表示为[6]

式中：μ0为浆液的初始黏度（Pa·s）；t为浆液拌合时间（s）；α为与浆液、介质的孔隙率有关的参数（s-1），可由试验获得。

浆液在地层中的渗透系数可表示为

式中：kw为水在地层中的渗透系数；β(t)=μ(t)/μw，为t 时刻浆液黏度与水的黏度比，由此可得考虑浆液黏度时变性的渗透系数为

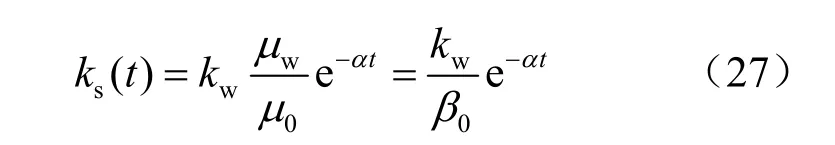
式中：β0为浆液初始黏度与水的黏度比：β0=μ0/μw。则式（24）可改写为

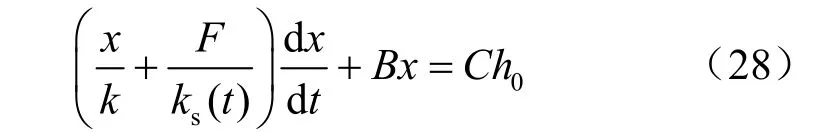
对上式进行求导，可得到考虑渗流阻力及地层渗透系数时变性作用下，浆饼x 随时间发生固结变形的计算公式 x(t) 。

根据式（6）、（7）和式（11）可推导出考虑时变性条件下浆液压力消散随时间变化的方程，即

式中：p浆t为t 时刻的浆液压力（MPa）；pt为t 时刻的渗透压力（MPa）。

4 工程验证

从上文公式推导可知，浆液固结厚度及浆液压力消散与地层孔隙水压力、地层渗透系数、浆体本身性质、注浆时间、初始时刻注浆压力大小等因素有关。实际盾构同步注浆过程中，应考虑上述因素对注浆压力控制的影响，防止因注浆压力过大引起的管片破损和地表隆沉。

基于长沙南湖路隧道北线河西漫滩段为工程[16]实例选取1 个代表性断面作为算例。该隧道断面顶部埋深约为10.79 m，上覆地层主要为粉土和粉细砂，地层渗透系数较大。地质剖面如图4 所示。该断面共设置6 个同步注浆孔，注浆口注浆压力设置从0.10～0.18 MPa 不等。

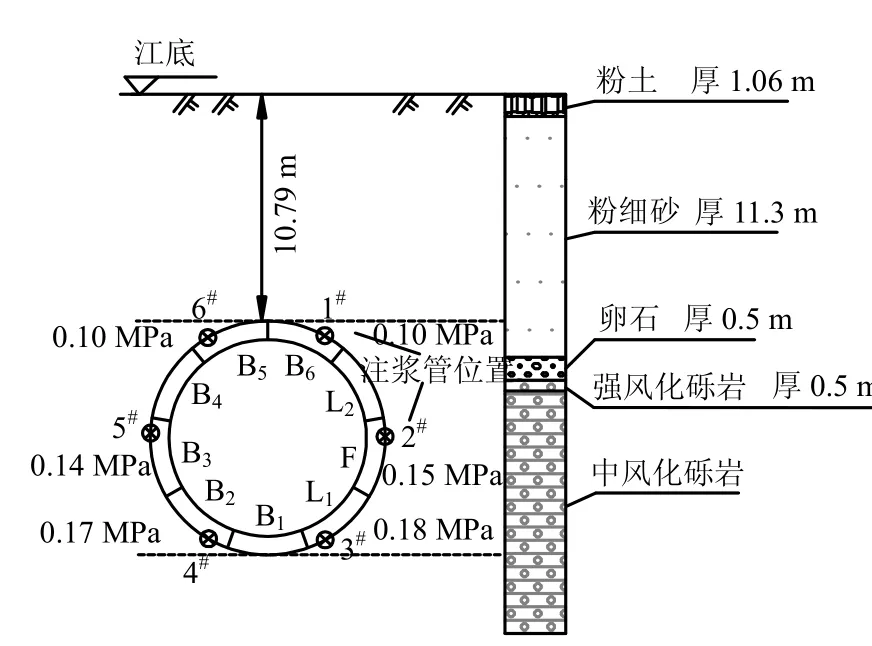
图4 典型地层地质剖面图Fig.4 Geological profile of typical layer

对工程现场使用的同步注浆浆液黏度随时间变化规律进行了试验研究。试验仪器为安东帕RheolabQC 旋转流变仪，可精准测量浆液的流变性规律，如图5 所示。

浆液配比及性质如表1 所示。

测定水泥浆液不同时刻的黏度值，结果如图6所示。

图5 旋转流变仪Fig.5 Rotational rheometer

表1 同步注浆浆液配合比Table 1 Synchronous grout mixture ratio

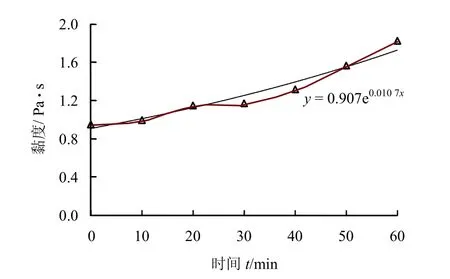
图6 浆液黏度随时间变化曲线Fig.6 Grout viscosity variation with time

通过数据拟合得到浆液黏度随时间变化的指数公式：μ(t)=0.907e0.0107t。

断面计算参数如表2 所示。

表2 工程实例计算参数表Table 2 Calculation parameters

综合文献[4]提出的浆液扩散公式和本文浆液消散式（29）可推导得到以注浆口为中心原点，注浆压力沿管片环分布的情况，如图7 所示。从图可知，浆液前期消散速率明显大于后期消散速率，由于浆液黏性的增大使浆液流动性减小，注浆压力消散速度明显小于不考虑浆液黏性变化（浆液黏度为常数）的情况。以3#注浆管（实测注浆口压力为0.18 MPa）作为算例，考虑浆液黏性变化的情况下，随着浆液逐渐固结，浆液压力逐渐稳定在0.145 MPa，相对于初始时刻注浆压力降低19.4%；若不考虑浆液黏性，浆液压力逐渐稳定在0.116 MPa，相对于初始时刻注浆压力降低35.6%。

为更好地掌握注浆压力对管片受力的影响，在管片环各管片内安装土压力盒、应变计、渗压计等监测原件对施工期间管片实际受力情况进行测试。其中渗压计共布设5 处（图中L2、L1、B1、B3、B5 管片内），用以测试盾尾同步注浆浆液压力。现场渗压计如图8 所示。

将渗压计实测结果与盾尾注浆管喷口处注浆压力进行对比，结果如图9 所示。从图中可知，浆液从注浆口喷出后，由于浆液固结变形及往周边地层扩散，浆液压力存在一定衰减。如3#注浆口附近实测得到的注浆压力为1.50 MPa，与理论计算结果接近。对比其余注浆孔处实测数据可知，注浆压力衰减幅度在16.6%～24.5%。管片环上部的注浆压力衰减幅度更大。现场实测结果证明了式（29）计算结果的合理性。在设置同步注浆压力时，应考虑浆液渗透及消散作用的影响。

图7 管片外壁浆液压力分布图Fig.7 Grout pressure distribution outside segment

图8 渗压计埋设示意图Fig.8 Pore water pressure gauge embedding schematic

图9 同步注浆压力实测结果(单位:kPa)Fig.9 Measured results of synchronous grouting、pressure(unit:kPa)

5 规律分析

5.1 浆液性质对固结厚度的影响

由式（24）和（28）计算得出浆液固结厚度随时间变化如图10 所示：若不考浆液黏性变化（浆液黏度为常数），则浆液在2 500 s 左右即完成大部分固结过程，浆液厚度仅为3.8 cm；若考浆液黏性变化，由于浆液黏性的增大使浆液流动性减小，因此，固结变形时间要长得多，且最终的浆液厚度与盾尾间隙厚度接近（0.1 m），与实际更加符合。

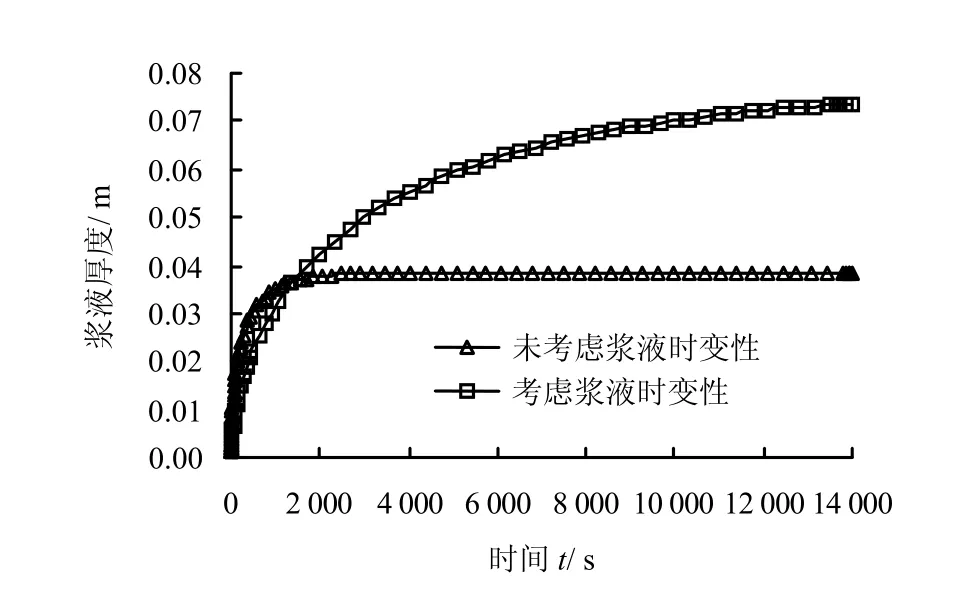
图10 浆液固结厚度随时间变化曲线Fig.10 Variations of grout consolidation thickness with time

5.2 浆液性质对浆液压力消散的影响

浆液配比不同，浆液黏度时变曲线也不同。基于文献[8]试验结果，由式（29）得到不同浆液性质条件下注浆压力随时间变化曲线如图11。若不考浆液黏性变化，则注浆压力消散幅度及浆液消散持续时间均明显大于考虑浆液黏性变化时的情况；在考虑浆液黏度时变性的条件下，浆液水灰比（w/c）越大，则注浆压力消散幅度越大。

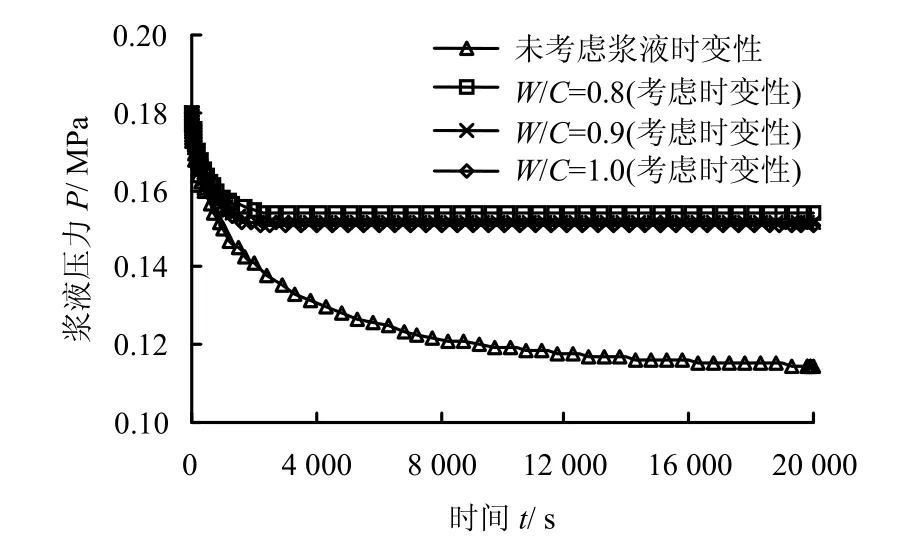
图11 不同浆液配比条件下注浆压力随时间变化曲线Fig.11 Grout pressure variation with time with different mixture ratio

5.3 地质条件对浆液压力消散的影响

不同地质条件下，围岩渗透系数差别较大。结合文献[14]中的工程实例及地质条件参数，由式（29）可得不同地质条件下（不同渗透系数）注浆压力随时间变化曲线如图12 所示。从图中可知，同等条件下，地层渗透系数越大（粉细砂地层 kw=8.68 ×10-5），注浆压力消散幅度越大，消散过程持续时间越长。

图12 不同地质条件下注浆压力随时间变化曲线Fig.12 Variations of grout pressure with time under different geological conditions

6 结 论

（1）浆液从注入至硬化的过程中，浆液中的水分会向周围地层渗透，浆液与地层的接触表层会发生固结变形，浆液压力随之逐渐消散。考虑到浆液往周边地层渗透过程中由于黏度的变化会引起地层渗透系数的变化，进而推导了考虑浆液黏度时变性的浆体固结变形方程和注浆压力消散方程。从公式推导可知，浆液固结厚度及压力消散与地层孔隙水压力大小、浆体性质、浆液黏度变化、初始时刻注浆压力大小等因素有关。实际盾构同步注浆过程中，应考虑上述因素对注浆量及注浆压力控制的影响。

（2）浆液从注浆口喷出后，浆液压力存在一定衰减，浆液压力前期衰减速率明显大于后期，若考虑浆液黏度时变性，则注浆压力消散速度明显减小。管片环上部的注浆压力衰减幅度更大。实测注浆压力衰减幅度与考虑浆液黏度时变性影响的理论计算结果较为一致，证明了计算结果的合理性。在实际注浆过程中，应充分考虑浆液消散及浆液黏度时变性对浆液压力控制的影响，适当增大浆液注入量，合理设定注浆压力。

（3）考虑浆液黏性变化的情况下，浆液黏性的增大使浆液流动性减小，浆液消散幅度减小，消散过程持续时间变短，浆液最终固结厚度与现场实际情况更加符合；浆液水灰比越大，则注浆压力消散幅度越大；地层渗透系数越大，注浆压力消散幅度越大，消散过程持续时间越长；反之亦然。

（4）本文在公式推导过程中假定浆液与扰动土体具有相同的弹性常数，即变形协调一致，且考虑了地层渗透系数的影响。在弹性模量较小，孔隙率较大的粉细砂地层中较为适用。但由于假定的局限性，在其他地层条件下，公式的适用性仍有待验证。

[1]LOMBARDI G.水泥灌浆浆液是稠好还是稀好[C]//现代灌浆技术译文集.北京:水利电力出版社,1991:76－81.LOMBARDI G.Should cement grout be thick or thin[C]//Collection of Translation of Modern Grouting Techniques.Beijing:Water Resources and Electric Power Press,1991:76－81.

[2]孙子正,李术才,刘人太,等.水泥基速凝浆液裂隙扩散机制与压力特性试验研究[J].岩土力学,2014,35(8):2219－2225.SUN Zi-zheng,LI Shu-cai,LIU Ren-tai,et al.Fracture defusing mechanism and pressure characteristic tests of rapid setting cement-based grouts[J].Rock and Soil Mechanics,2014,35(8):2219－2225.

[3]叶飞,朱合华,何川.盾构隧道壁后注浆扩散模式及对管片的压力分析[J].岩土力学,2009,30(5):1307－1312.YE Fei,ZHU He-hua,HE Chuan.Back-filled grouts diffusion model and its pressure to segments of shield tunnel[J].Rock and Soil Mechanics,2009,30(5):1307－1312.

[4]叶飞,苟长飞,刘燕鹏,等.盾构隧道壁后注浆浆液时变半球面扩散模型[J].同济大学学报(自然科学版),2012,40(12):1789－1794.YE Fei,GOU Chang-fei,LIU Yan-peng,et al.Halfspherical surface diffusion model of shield tunnel back-filled grouts[J].Journal of Tongji University(Natural Science),2012,40(12):1789－1794.

[5]苟长飞.盾构隧道壁后注浆浆液扩散机制研究[D].西安:长安大学,2013.GOU Chang-fei.Study on the grouts diffusion mechanism of shield tunnel back-filled grouts[D].Xi'an:Chang'an University,2013.

[6]白云,戴志仁,张莎莎,等.盾构隧道同步注浆浆液压力扩散模式研究[J].中国铁道科学,2011,32(4):38－45.BAI Yun,DAI Zhi-ren,ZHANG Sha-sha,et al.Study on the grout pressure dissipation mode in simultaneous backfill grouting during shield tunneling[J].China Railway Science,2011,32(4):38－45.

[7]李志明,廖少明,戴志仁.盾构同步注浆填充机制及压力分布研究[J].岩土工程学报,2010,32(11):1752－1757.LI Zhi-ming,LIAO Shao-ming,DAI Zhi-ren.Theoretical study on synchronous grouting filling patterns and pressure distribution of EPB shield tunnels calculating model of backfill grouting pressure distribution for shield tunnel[J].Chinese Journal of Geotechnical Engineering,2010,32(11):1752－1757.

[8]袁小会,韩月旺,钟小春.盾构隧道壁后注浆压力分布模型[J].西南交通大学学报,2011,46(1):18－23.YUAN Xiao-hui,HAN Yue-wang,ZHONG Xiao-chun.Pressure distribution model of simultaneous backfill grouting of shield tunnel[J].Journal of Southwest Jiaotong University,2011,46(1):18－23.

[9]刘健,张载松,韩烨,等.考虑黏度时变性的水泥浆液盾构壁后注浆扩散规律及管片压力模型的试验研究[J].岩土力学,2015,36(2):361－368.LIU Jian,ZHANG Zai-song,HAN Ye,et al.Backfilled grouting diffusion law and model of pressure on segments of shield tunnel considering viscosity variation of cement grout[J].Rock and Soil Mechanics,2015,36(2):361－368.

[10]BEZUIJEN A,TALMON A M,KAALBERG F,et al.Field measurements of grout pressures during tunneling of the Sophia rail tunnel[J].Soils and Foundations,2004,44(1):39－48.

[11]阮文军.注浆扩散与浆液若干基本性能研究[J].岩土工程学报,2005,27(1):69－73.RUAN Wen-jun.Research on diffusion of grouting and basic properties of grouts[J].Chinese Journal of Geotechnical Engineering,2005,27(1):69－73.

[12]阮文军.基于浆液黏度时变性的岩体裂隙注浆扩散模型[J].岩石力学与工程学报,2005,24(15):2709－2714.RUAN Wen-jun.Spreading model of grouting in rock mass fissures based on time-dependent behavior of viscosity of cement-based grouts[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(15):2709－2714.

[13]李术才,韩伟伟,张庆松,等.地下工程动水注浆速凝浆液黏度时变特性研究[J].岩石力学与工程学报,2013,32(1):1－7.LI Shu-cai,HAN Wei-wei,ZHANG Qing-song,et al.Research on time-dependent behavior of viscosity of fast curing grouts in underground construction grouting[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(1):1－7.

[14]韩月旺,钟小春,虞兴福.盾构壁后注浆体变形及压力消散特性试验研究[J].地下空间与工程学报,2007,3(6):1142－1147.HAN Yue-wang,ZHONG Xiao-chun,YU Xing-fu.Experimental research on the backfill grout deformation and grout pressure dissipation of shield tunnel[J].Chinese Journal of Underground Space and Engineering,2007,3(6):1142－1147.

[15]张莎莎,戴志仁,白云,等.盾构隧道同步注浆浆液压力消散规律研究[J].中国铁道科学,2012,33(3):40－48.ZHANG Sha-sha,DAI Zhi-ren,BAI Yun,et al.Research on dissipation law of grout pressure during the simultaneous grouting of shield tunnel[J].China Railway Science,2012,33(3):40－48.

[16]陈相宇.盾构施工引起的富水地层孔隙水压力反应分析及控制研究[D].长沙:中南大学,2014.CHEN Xiang-yu.Research on pore pressure reaction caused by slurry shield tunneling in watery strata and its control technology[D].Changsha:Central South University,2014.