基于修正D-S证据理论的锚杆承载力预测方法研究
2015-02-17孙晓云王明明
孙晓云,张 涛,王明明,邢 卉
(石家庄铁道大学 电气与电子工程学院,河北 石家庄 050043)
1 引 言
随着我国岩土锚固工程迅速发展,锚杆承载力检测已经成为一个焦点。传统的锚杆承载力检测方式是通过对锚杆进行现场拉拔试验,测定锚杆部分荷载P 和位移S 数据,建立数学模型,进而预测完整的锚杆承载力及极限承载力值。所以模拟锚杆P-S 曲线精度高和预测锚杆极限承载力准确度高的模型一直是研究的焦点。
应志民[1]、邓志勇[2]等使用双曲线和指数模型对锚杆和单桩荷载-位移曲线进行模拟,并对比和分析了各自的实用性;赵明华[3-4]、蒋建平[5]等对双曲线模型进行修正,分别提出了调整双曲线和修正双曲线模型,并用来预测锚杆和桩的极限承载力;龙照[6]建立了由双曲线和指数模型组合而成的最优组合预测模型;上述文献对锚杆P-S 曲线进行模拟时,都没有考虑到实际情况(大多数锚杆都为预应力锚杆,锚杆都必须施加预应力才能起到主动支护的作用,且实际锚杆拉拔试验测量数据存在误差),而直接按照理论锚杆P-S 曲线的形状去建立和改进模型,强制模型过原点,易导致建立的模型通用性较差、只对一些特定的数据模拟精度较高、预测极限承载力准确度较高的缺点。
刘明贵等[7]引入了锚杆承载力的灰色系统预测法;白坡等[8]使用了幂函数模型模拟桩的荷载-位移曲线;杨群[9]提出了支盘桩试桩极限承载力的二次趋势曲线预估法;李军亮[10]论证了桩和锚杆的荷载-位移曲线的相似性,用来模拟桩的模型也可以用来模拟锚杆的荷载-位移曲线,而且提出了广义灰色模型的锚杆和桩基极限承载力建模方法。所以幂函数模型和二次趋势曲线预估法也可以用来模拟锚杆P-S 曲线。上述文献对锚杆P-S 曲线进行模拟时,都没有考虑到实际情况。刘思思等[11]根据抗拔锚杆试验数据,建立了锚固体荷载传递特性随锚固深度变化的动态折线数值计算模型,在试验分析及工程设计中起到辅助作用,为更精细的计算锚杆承载力提供了参考。而张昌锁[12]、王猛[13]、张胜利[14]很早就开始研究锚杆无损检测方法,并取得了很大的进步;宋伟等[15]在分析锚杆锚固质量无损检测原理的基础上,提出了以Hilbert 变换为基础的数据,并证实了可行性;Starkey[16]、Vrkljan 等[17]分别利用空气锤和铁锤对锚杆锚固的顶端进行敲击,并采集了反射信号,得出了锚固系统的固有频率随锚固锚杆的轴向承载力增加而增大的结论,并提取主频,对锚杆锚固段的质量进行了分析。上述文献多涉及到锚杆质量无损检测,对锚杆受力检测研究得较少。
在实际工程中,锚杆P-S 曲线多种多样,使用单一的模型并不能都准确预测各类锚杆极限承载力值,这就产生了多模型组合预测的需要。锚杆极限承载力值由锚杆极限承载力破坏值(锚杆破坏荷载值)决定[18],故关键是准确预测锚杆极限承载力破坏值。通过建模预测锚杆极限承载力破坏值是一种不确定问题,本文引入D-S 证据理论融合算法[19]来产生组合预测模型,并做了预测锚杆极限承载力破坏值准确度对比。
2 预测模型简介
能够用来对锚杆极限承载力值进行预测的模型有双曲线模型[1-2]、调整双曲线模型[3-4]、修正双曲线模型[5]、幂函数模型[8]、指数模型[1-2]、改进指数模型[20]、改进指-幂混合函数模型、多项式模型[9]以及非等间距灰色GM(1,1)模型[7]和分段GM(1,1)模型[21]等。现对多项式模型和改进指-幂混合函数模型进行简单介绍,其余模型参见各对应文献。
修正双曲线模型和调整双曲线模型,是在原有双曲线模型结构的基础上,分别引入了幂函数和多项式函数得到的,与双曲线模型相比,精度得到了较大提高。在一定程度上,适当地引入其他类函数可以提高模型的模拟精度,通过不同类函数的协调调节,增大调整范围,使模拟曲线更加接近于实际曲线,改进指-幂混合函数模型就是在改进指数模型的基础上引入幂函数模型得到的,对应方程为

式中:P、S、Pu分别代表某一级别的荷载(kN)、某一级别的荷载下锚杆端头位移(mm)和待求锚杆的极限承载力破坏值(kN);a、b、c、k1均为待拟合参数。
文献[9]中引入二次多项式模型模拟桩基的荷载-位移曲线,同样二次多项式模型也可以用来模拟锚杆的荷载-位移曲线[10],但二次多项式模型调节能力小,预测锚杆的极限承载力破坏值准确度较差。然而三次多项式模型模拟效果较好,其方程为
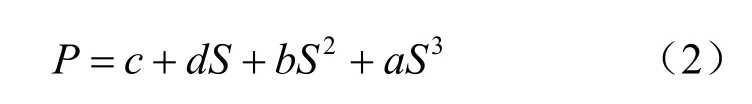
预测锚杆的极限承载力值取为
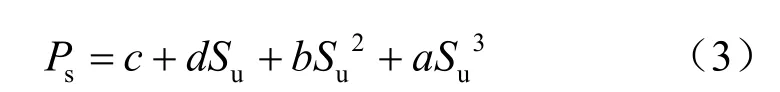
预测锚杆极限承载力破坏值为
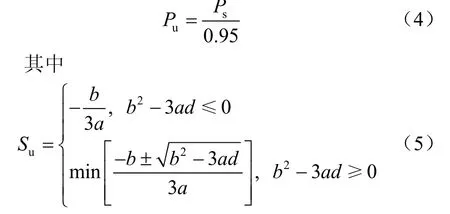
由于实测锚杆荷载和位移数据较少,有可能建立的三次多项式模型为类S 型形状,故在使用三次多项式进行建模时,要根据实际情况进行修正。三次多项式模型建立过程如图1 所示,主要步骤说明如下:
(1)模型参数识别。使用线性回归法求取三次多项式模型参数,具体如下:
步骤1:一元变多元,令x1=S,x2=S2,x3=S2,y=P。

步骤2:求取矩阵B1、B2,其中,(i、k=1、2、3;i≠k),n为 x1、x2、x3和y 中的数据个数。
步骤3:求取多项式参数矩阵C 和参数c。

(2)预测锚杆极限承载力和极限位移。将(1)中求解得到的模型参数,带到式(4)中,求取极限位移 Su;再将 Su带到式(3)中,求取极限承载力值Ps。
(3)修正判定。将(2)中极限位移值与各荷载下实测位移值进行对比,若极限位移值大于各荷载下实测位移值,则无需对三次多项式模型进行修正。反之,则需要使用直线法对三次多项式模型进行修正。
(4)模型修正。以预测极限位移值 Su作为分界点,实测位移S 比 Su小的阶段曲线重新使用三次多项式进行模拟,将此阶段模拟得到的最后一对S 和P 值,以及后续已知的实测锚杆荷载P 和位移S 的数据,按照误差平方和最小的原则,进行直线拟合。重新建立的三次多项式模型,预测的锚杆极限承载力值作为锚杆极限承载力最终预测值。按照式(5)求取锚杆极限承载力破坏值。
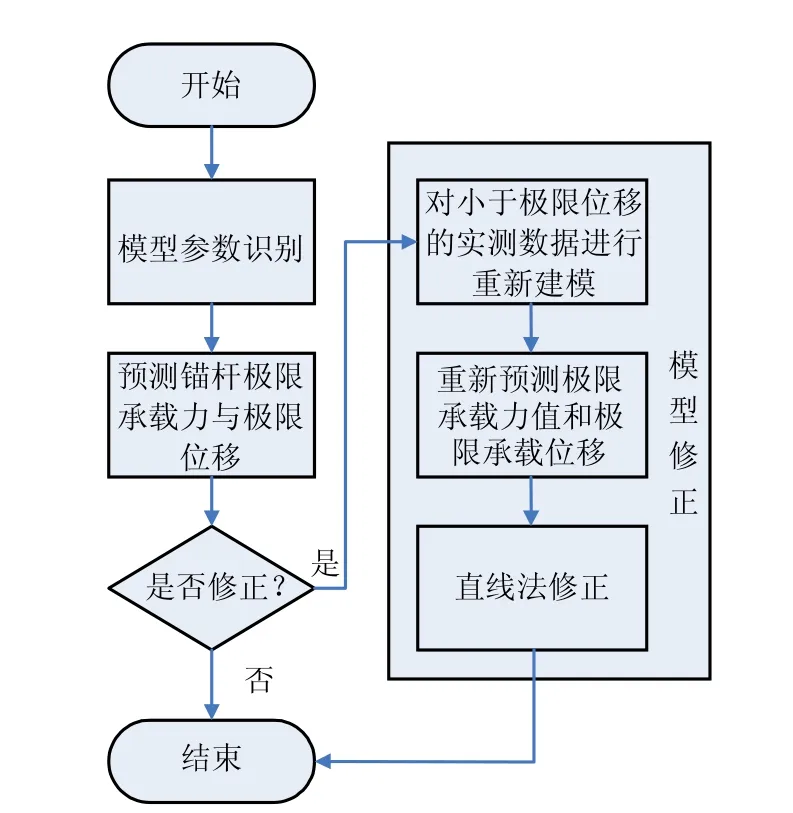
图1 三次多项式模型建立流程图Fig.1 The flow chart of cubic polynomial model
3 D-S 证据理论及算法实现
将各模型的锚杆极限承载力破坏值预测结果与实际测值进行比较,会出现模型的预测值都偏大、偏小或分布在实测值两侧3 种可能。当所有模型预测值都偏小,将各模型预测的极限承载力值最大的作为最终预测值,误差最小;同理,当所有模型预测值都偏大,将各模型预测的极限承载力值最小的作为最终预测值,误差最小;在实际模拟预测中,大多数情况预测值分布在实测值两侧,对各模型预测的极限承载力值求取算术平均值,把这个平均值作为最终预测值,若选择的模型适当,误差很小,甚至有可能实现无静差。预测锚杆极限承载力破坏值是一种不确定问题,使用多个预测模型生成多个预测值,就可以使用D-S 证据理论融合算法进行较高精度预测。
Dempster 于1967年首次提出证据理论,后由其学生Shafer 进行了扩展[19],建立了对不确定信息进行处理的证据理论。D-S 证据理论从可能成立的条件中分离出前提严格的条件,使任何涉及先验概率的信息缺失得以显示化,能区分未知性和不确定性[19,22]。
该证据理论被广泛用在多传感器信息融合中,它的实质就是将每一个传感器视为一个证据体,在同一鉴别框架下,把不同特征的证据体按照某一规则合并成一个新的证据体的过程。再根据某种决策方法得到最终的判定结果[23]。以此类推,将D-S 证据理论应用到多预测模型数据融合中也是可行的,把预测模型的相关预测数据作为该理论中的证据体,构成对待识别目标模式的信度函数(表示每个证据对目标模式假设的可信程度)分配,然后使用D-S 理论合并规则,将n 个证据合成一个新的证据,为决策目标模式提供准确、综合的信息。图2为D-S证据理论的信息融合原理示意图,图中 m1(A),m2(A),…,mn(A) 分别表示n 个预测模型对命题A的基本可信度分配,通过D-S 理论合并规则合成基本可信度分配 m(A),然后运用决策规则进行决策,识别结果。具体实现过程可以分为4 部分,具体如下所示:
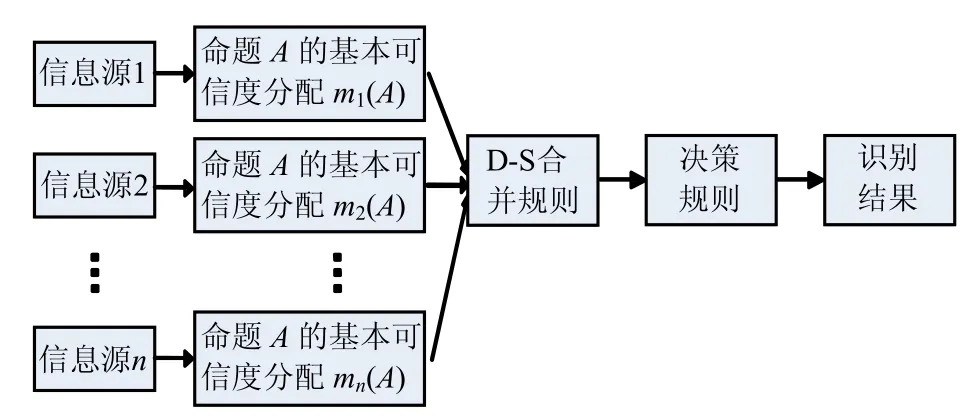
图2 D-S 证据理论融合原理图Fig.2 The fusion principle diagram of D-S evidence theory
(1)确定辨识框架。辨识框架是D-S 证据推理的基础,D-S 证据理论中每一个函数和概念都是建立在辨识框架的基础上。对于一个判断问题,将所能预测到的可能结果用集合Θ 表示,这样关心的任何一个命题都可对应于Θ 的一个子集,这里将集合Θ 称为辨识框架。
(2)基本概率赋值。假设Θ为一个有穷而完备的集合,并且集合Θ 中各元素相互独立。对于任何属于Θ 的命题A 都有函数m:2Θ→[0,1](2Θ代表集合Θ 中的所有子集),且满足:

式(6)称为 m(A)为命题A 的基本概率分配,用来表示对命题A 的精确信任程度。本文为了减小计算的复杂度,仅使用单元素命题A,加入融合模型选择这一环节(详见第4 节)。在实际中并不知道命题A 发生的概率,故引入模糊数学的模糊数理论来进行基本概率分配。模糊数有多种类型,究竟采用哪种类型要结合实际问题来确定,选择依据是所选用的模糊数应具备一定程度的合理性,易于后续数据处理[24]。
在实际中,从可信度的角度来看,锚杆极限承载力预测值距离真实值越近,则可信度就应该越高,曲线下降也应该较缓;反之,越远可信度就越低,曲线下降也较陡;当大于或小于某值,可信度极小。故使用高斯模糊数更为合适,高斯模糊数可表述为图3,其隶属函数为

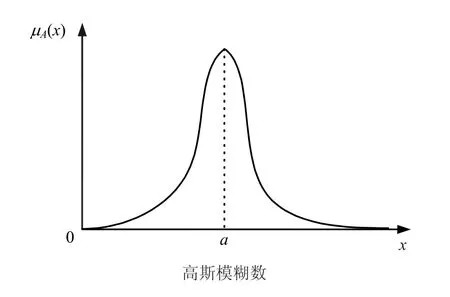
图3 高斯模糊数示意图Fig.3 The schematic diagram of Gaussian fuzzy numbers
使用高斯模糊数进行基本概率分配方法为:将每根锚杆的全部预测数据中一个最大值 Pmax和一个最小值 Pmin去掉,对其余数据,求取平均值 Pav,将这个数据作为a 的值。本文为了增大各模型之间可信度的对比度,取
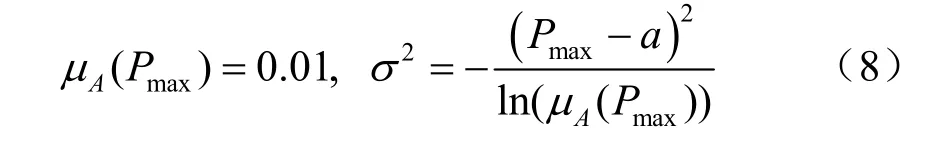
(3)D-S 证据合并。D-S 证据合并严格按照D-S证据合并规则进行,D-S 证据合并规则是综合多个预测模型的基本可信度分配,合并成一个新的基本可信度分配。合并规则也称作正交和规则,用⊕表示。假设 m1和m2是Θ 上的两个概率分配函数,x和y 是Θ 中包含于A 的任意两个子集,则使用D-S证据合并规则合并后的命题A 的基本概率分配为

式中:A≠φ,φ为空集,m(φ)=m1(φ)=m2(φ)=0,c-1为冲突因子,各证据间的冲突越大,c-1值越大,

D-S 合并规则仅提供了组合2 个证据的合并规则,要对于多个证据进行融合,可重复利用式(9)对多个证据进行两两组合。合并规则满足交换律和结合律,即有:m1⊕m2=m2⊕m1;(m1⊕m2)⊕m3=m1⊕(m2⊕m3)。
(4)结果决策。结果决策也有相应的决策规则,目标不同决策规则不同。本文使用D-S 证据理论进行较优融合模型选择和数据融合预测结果两项内容,故有2 个决策规则:
规则1(以选择较优融合模型为目标):以数值1/M 来选择模型好与坏,当数据融合后最终基本概率赋值数大于等于1/M 时,就认为这个模型为较好模型,反之这个模型为较差模型,其中M为参与运算的模型个数,
规则2(以选择最优预测结果为目标):把融合后最终基本概率赋值数最大的数据范围认为最可靠范围,对这个最可靠范围的数据求取算式平均值,作为最终预测结果。
4 承载力预测方法
用D-S 证据理论融合算法实现锚杆极限承载力预测的过程,主要包括特征值提取、融合模型选择和数据融合预测3 个方面。
(1)特征值提取。特征值提取就是提取各预测模型预测的极限承载力破坏值。适当地减少弹性阶段数据,有助于提高预测锚杆极限承载力破坏值的准确度,故这里通过减少弹性阶段的数据量的方法,使各模型都能产生多个预测精度较高的预测值。
在实际工程中,由于拉拔试验较困难,采集的数据可能较少,减少数据反而有可能会降低预测精度,故在较少的原始数据上需要增添适量数据。由于预测精度受弹性阶段数据影响较大,故对实测数据在弹塑性阶段曲线进行三次样条插值。
(2)融合模型选择。融合模型选择可以使用D-S证据理论融合算法实现,以选择较优融合模型为目标,把各数据范围下预测的极限承载力破坏值作为证据体,使用D-S 理论合并规则将多个证据体合成一个新的证据体,运用决策规则1 决策目标,选择出较优融合模型组合。若运用决策规则2 决策目标,则可以选出最优模型,对它在各个范围内的预测值求取平均值,作为最优模型预测值。
(3)数据融合预测。数据融合预测就是以选择最优预测结果为目标,将参与融合的各模型预测的极限承载力破坏值作为证据体,使用D-S 理论合并规则将多个证据体合成一个新的证据体,运用决策规则2 决策目标。但在数据融合预测前先要判断是否需要进行这一步,根据第3 节开始的分析结果,只有当参与融合的各模型预测值分布在实测值两侧时,才需要进行数据融合预测。具体判别方法在6.1节中详述。
5 修正的预测方法
前文所述的预测方法,预测精度受模糊数中参数a 的影响较大(从后文锚杆E 的预测结果中能够证明)。针对此种现象,在原有预测方法的基础上,添加了修正环节,对原有预测方法进行修正,具体实现过程如图4 所示,图中虚线框内部分即是修正环节。

图4 修正后的预测方法流程图Fig.4 The flow chart of the revised prediction method
在修正过程中,基本概率分配所使用的模糊数参数a 取原有预测方法的最终预测值,此值与真实值相比误差较小,故此时选择的模型组合更为合适,都为较高精度预测模型,无需再判断模型预测值是否分布在实测值两侧,误差不会相差很大。
6 工程案例验证
使用文献[25]中的5 根锚杆拉拔试验数据,其中锚杆A 和B 的破坏阶段数据较丰富,但都存在凹点,锚杆B 的P-S 曲线较锚杆A 光滑,锚杆C 的破坏阶段数据较少,锚杆D 和E 没有出现破坏阶段数据,锚杆C、D 和E 的P-S 较光滑。使用这5 根锚杆的实测数据检验基于D-S 证据理论的数据融合算法在锚杆极限承载力预测中的应用效果是非常合适的,具体数据如表1 所示。
6.1 预测方法验证试验
以锚杆A为例进行详细说明,具体实现步骤如下:
(1)特征值提取。使用修正双曲线模型、调整双曲线模型、指数模型、改进指数模型、改进指-幂模型、三次多项式模型、GM(1,1)模型和分段GM(1,1)模型对锚杆A 进行建模,预测极限承载力破坏值。使用减少低量值荷载数据的方法,使每个预测模型对锚杆A 都预测4 个极限承载力破坏值,使用数据范围为表2 中编号1~9、2~9、3~9、4~9。
对表2 进行分析可以发现,调整双曲线模型预测极限承载力破坏值准确度最差,且偏大。将表2中预测值与各锚杆的实测值进行比较,对于锚杆C,除调整双曲线以外,各模型预测值都偏小。其余锚杆预测值分布在实测值两侧。除锚杆C 以外,改进指-幂混合函数模型的预测值误差都较小。对表2中指数模型和改进指数模型进行分析可以发现,当指数模型预测值都大于改进指数模型预测值时,除调整双曲线的以外,其余模型预测值都偏小,而且除个别数值以外,都不比指数模型预测值大。
综上所述,可以使用指数与改进指数模型预测值之间的大小关系,以及改进指-幂混合函数模型各预测值的平均值,来判断参与融合预测的模型是否分布在实测值两侧。
(2)融合模型选择。以选择较优融合预测模型为目标,确定锚杆各组数据的基本概论分配,详见表3。使用式(9)对表3 中的锚杆A 的各证据体进行融合,各个融合步骤的证据累积结果见表4。
根据融合结果,按照决策规则1,从表3 可以看出,改进指-幂模型、三次多项式模型和分段GM(1,1)模型为较好模型,改进指-幂模型模型精度可信度最高,若对它的4 个预测值求取算式平均值,作为最终预测值,预测结果为:668.08 kN,与实测值665.8 kN 相比,误差仅为0.32%。
(3)数据融合预测。根据融合模型选择的结果可以看出:改进指-幂模型、三次多项式模型和分段GM(1,1)模型这3 个模型的预测效果较好,预测值分布在实测值两侧,取锚杆A 的辨识框架θ={N1,N2,N3,N4}={661.78,677.08,662.62,664.92}。根据高斯模糊数计算方法,锚杆A 各组数据的基本概论分配及各个融合步骤的证据累积的结果如表4所示。
从表可以看出,随着证据的累积,锚杆A 融合结果对N4命题的支持度增大且最大,根据决策规则2 可以判断锚杆A 的极限承载力破坏值最终预测结果为664.92 kN,与实际测量值665.8 kN 相比,误差仅为-0.132%,误差很小。

表1 锚杆拉拔试验实测数据Table 1 The measured data of rock bolt pull-out test
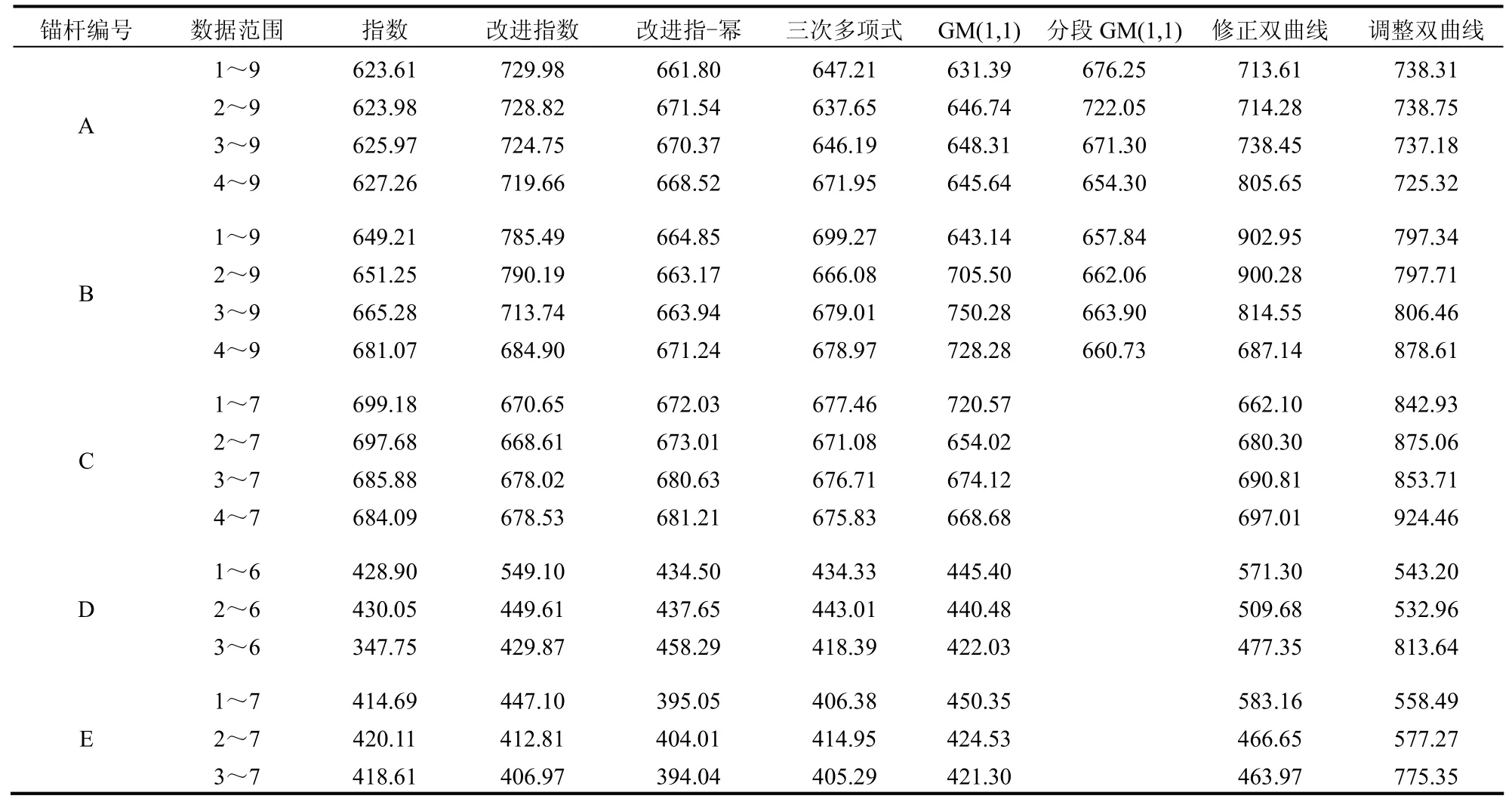
表2 各模型预测极限承载力破坏值(特征值)(单位:kN)Table 2 Predicted ultimate bearing capacity values of different models(eigenvalue)(unit:kN)

表3 锚杆A 的各证据体的可信度分配和融合结果(融合模型选择)Table 3 Reliability distribution and fusion result of each evidence on rock bolt A(fusion model selection)

表4 锚杆A 的各证据体的可信度分配和融合结果(数据融合预测)Table 4 Reliability distribution and fusion result of each evidence on rock bolt A(data fusion prediction)
按照上述方法,对锚杆B、C、D 和E 进行极限承载力破坏值预测,各模型预测结果如表5 所示。由于锚杆C、D 和E 较光滑,建立的分段GM(1,1)模型和GM(1,1)模型预测结果基本一样,故不使用分段GM(1,1)模型对这3 根锚杆进行进行极限承载力破坏值预测。对于锚杆C,通过融合模型选择后,参与数据融合预测的较高精度模型的预测值均偏小,直接将最大值697.68 kN 作为最终预测值;除此以外,对于其他锚杆,参与数据融合预测的较高精度模型的预测值均位于实测值两侧,预测结果如表5 所示。
6.2 修正的预测方法验证试验
同样以锚杆A为例进行详细说明,将高斯模糊函数中的a 取为664.92,对修正双曲线模型、调整双曲线模型、指数模型、改进指数模型、改进指幂混合函数模型、三次多项式模型、GM(1,1)模型和分段GM(1,1)模型进行融合模型选择,锚杆A 各组数据的基本概论分配,详见表6。使用式(8)对表6 中锚杆A 的各证据体进行融合,各个融合步骤的证据累积的结果同样如表6 所示。
根据表中的融合结果,按照决策规则1 进行判定,改进指幂混合函数模型、三次多项式模型、GM(1,1)模型和分段GM(1,1)模型较优,使用这4 个模型进行数据融合预测,此时锚杆A 的辨识框架θ={ N1,N2,N3,N4}={654.18,669.50,659.04,660.10}。根据高斯模糊数计算方法,锚杆A 各组数据的基本概论分配及各个融合步骤的证据累积的结果如表7 所示。
从表可以看出:随着证据的累积,根据锚杆A的融合结果,按照决策规则2 可以判断锚杆A 的最终预测极限承载力破坏值为660.10 kN,与实际测量值665.80 kN 相比,误差为-0.856%。按照上述方法,对锚杆B、D 和E 进行修正后预测方法试验验证,预测结果详见表8,与原预测方法相比,误差更小。

表5 极限承载力破坏值的预测结果Table 5 The predicted results of the ultimate bearing capacity value of failure
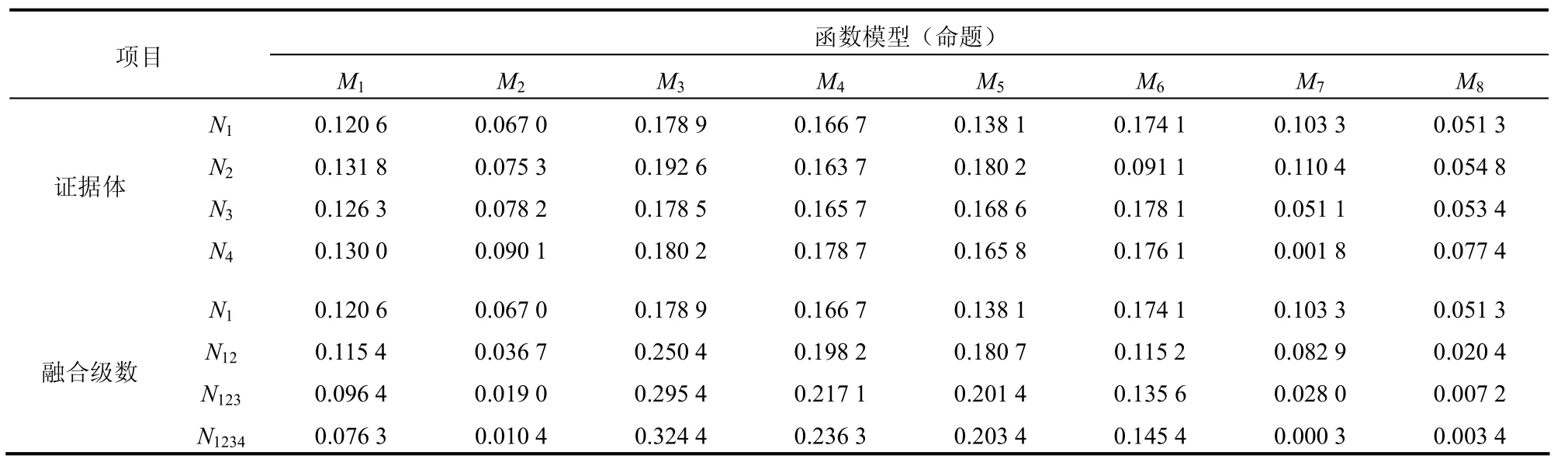
表6 锚杆A 的各证据体的可信度分配和融合结果(融合模型选择、修正)Table 6 Reliability distribution and fusion result of each evidence on rock bolt A(fusion model selection,correction)

表7 锚杆A 的各证据体的可信度分配及各证据体的融合结果(数据融合预测、修正)Table 7 Reliability distribution and fusion result of each evidence on rock bolt A(data fusion prediction,correction)

表8 极限承载力破坏值的预测结果(修正的预测方法)Table 8 The predicted results of the ultimate bearing capacity value of failure(the revised forecast method)
6.3 预测结果分析
结合表2、5、8 进行分析,三次多项式模型和改进指-幂混合模型预测效果都较好。通过融合模型选择的结果可以发现:预测5 根锚杆的较好模型几乎都有改进指-幂模型和三系多项式模型。故使用改进指-幂模型和三次多项式模型来预测锚杆极限承载力破坏值是可行的。
建立预测模型,由于实测锚杆拉拔数据有限,并且不能明显区分开弹性和弹塑性阶段数据,使用单一模型进行预测有可能产生较大误差;在实际工程中,锚杆P-S 曲线多种多样,使用单一预测模型不能都准确预测出各类锚杆极限承载力破坏值。而使用D-S 证据理论融合算法可以选出最优预测模型,也可以建立组合预测模型,其预测结果精度都很高,且适用范围都更广。
对表5 进行分析,结果如下:
(1)就原有D-S 证据理论融合算法本身而言,直接使用融合模型选择环节中的最优模型的预测平均值作为最终预测值,与数据融合预测结果相比,总体上后者预测精度更高一些。
(2)除锚杆C 以外,D-S 证据理论预测方法的预测精度高于直接求取算术平均值的组合方式,这是由于D-S 证据理论预测方法能选择出较高精度预测模型和较好数据范围。
(3)对于锚杆C,由于预测锚杆C 的较高精度预测模型的预测值都偏小,严格按照D-S 证据理论预测方法的步骤,预测结果为697.68 kN,误差为-2.327,但引入预测精度很差的调整双曲线模型和较差的GM(1,1)模型后,经过数据融合预测这一环节后,预测精度得到了很大提高,预测结果为705.70 kN,误差仅为-1.204,高于直接求取算术平均值的组合方式,故在实际使用中,当出现类似锚杆C 这种情况,可以酌情加入一个或多个预测精度较差的模型。
(4)对于锚杆D 和E,D-S 证据理论预测方法的预测精度明显高于直接求取算术平均值的组合方式,锚杆D 的预测精度较高,但锚杆E 的预测精度相对差一点,这是由于使用高斯模糊数进行可信度分配时,选择平均值454.36 kN 作为参数a 的值,此值与真实值偏差过大造成的。若以真实值作为参数a 的值,对锚杆E 进行预测,参与融合的模型变为指数模型、改进指数模型、改进指-幂模型、三次多项式模型和 GM(1,1)模型,最终预测结果为407.19 kN,误差仅为0.476%。
将表5 和表8 进行对比分析,结果如下:
(1)直接使用融合模型选择环节中的最优模型的预测平均值作为最终预测值,预测方法修正前后的预测结果仅锚杆E 发生变化,修正后的预测结果误差变得更小。
(2)对预测方法修正前后的数据融合预测结果进行比较,除锚杆A 以外,其余锚杆使用修正后预测方法的预测精度更高。虽然锚杆A 修正后的预测结果误差变大,但总体上看,修正后预测方法好于修正前,预测效果更好。
(3)在表8 中,最优预测模型和数据融合预测结果差别不大,预测精度都很高。这也就证实了使用D-S 证据理论融合算法来选取最优预测模型和产生组合预测模型(数据融合预测)的可行性。数据融合预测结果与实测值相比略微偏小一点,因此,在实际工程中预测结果更为可靠一些。
(4)最优预测模型预测和数据融合预测都是在算术平均值预测的基础上,使用D-S 证据理论融合算法来达到较高精度预测锚杆极限承载力破坏值的目的,故它们的计算效率均低于算术平均值预测方法,但与通过对锚杆进行破坏性拉拔试验以获得锚杆极限承载力破坏值的时间相比,显得微乎其微,并且使用它们能够减小对锚杆的破坏程度和试验危险程度,缩短拉拔试验时间和降低资金投入。
7 结 论
(1)使用改进指-幂混和函数模型和三次多项式模型来预测锚杆极限承载力值是可行的,预测效果都较好。
(2)D-S 证据理论预测方法具有选择较高精度预测模型和最好数据范围的功能,通过融合模型选择选出较高精度预测模型,作为较优融合模型组合,参与数据融合预测,选出最好数据范围,对最好数据范围内的较高精度预测模型的预测值求取平均值,作为最终预测值。此方法预测精度较高,比直接使用求取算术平均值的方法预测效果要好,具有很高的研究价值。
(3)在原有D-S 证据理论预测方法的基础上进行修正,修正后预测方法的预测效果更好,预测精度更高。
[1]应志民,张洁,尚岳全.锚杆荷载-位移曲线的指数函数模型研究[J].岩土力学,2005,26(8):1331-1334.YING Zhi-min,ZHANG Jie,SHANG Yue-quan.Exponential model for simulating load-displacement curve of anchor rod[J].Rock and Soil Mechanics,2005,26(8):1331-1334.
[2]邓志勇,陆培毅.几种单桩竖向极限承载力预测模型的对比分析[J].岩土力学,2002,23(4):428-431,464.DENG Zhi-yong,LU Pei-yi.Comparison and analysis of several predicting models of ultimate bearing capacity of single pile[J].Rock and Soil Mechanics,2002,23(4):428-431,464.
[3]赵明华,张天翔,邹新军.支挡结构中锚杆抗拔承载力分析[J].中南公路工程,2003,28(4):4-7.ZHAO Ming-hua,ZHANG Tian-xiang,ZOU Xin-jun.Analysis of anti-pull-force for anchored bars in retaining structures[J].Central South Highway Engineering,2003,28(4):4-7.
[4]赵明华,胡志清.预估试桩极限承载力的调整双曲线法[J].建筑结构,1995,(3):47-52.ZHAO Ming-hua,HU Zhi-qing.The adjustment hyperbolic method of estimated test pile ultimate bearing capacity[J].Journal of Building Structures,1995,(3):47-52.
[5]蒋建平,高广运,刘文白.描述抗拔挤扩支盘桩Q-s 曲线的修正双曲线模型研究[J].应用基础与工程科学学报,2010,18(6):999-1009.JIANG Jian-pin,GAO Guang-yun,LIU Wen-bai.Modified hyperbolic model describing Q-s curves of squeezed branch pile[J].Journal of Basic Science and Engineering,2010,18(6):999-1009.
[6]龙照.锚杆抗拔承载机理及其在基桩自锚测试技术中的应用[D].长沙:湖南大学,2007.LONG Zhao.Uplift mechanism of bolt and its application in self-anchored loading test technology of pile foundation[D].Changsha:Hunan University,2007.
[7]刘明贵,杨永波,岳向红,等.基于灰色系统理论的锚杆极限抗拔力预测方法[J].地下空间与工程学报,2006,2(6):1044-1048.LIU Ming-gui,YANG Yong-bo,YUE Xiang-hong,et al.The prediction method of ultimate resistance capacity of bolt base on gray theory[J].Chinese Journal of Underground Space and Engineering,2006,2(6):1044-1048.
[8]白坡,魏庆龙,王宁.基于幂函数模型预估等截面抗拔桩单桩极限承载力的试验研究[J].粮食流通技术,2010,(6):9-13.BAI Po,WEI Qing-long,WANG Ning.Research on ultimate uplift capacity of tension piles of uniform section based on prediction of power function model[J].Grain Distribution Technology,2010,(6):9-13.
[9]杨群.支盘桩试桩极限承载力的二次趋势曲线预估法[J].科学技术与工程,2009,9(14):4230-4233.YANG Qun.Prediction method for ultimate bearing capacity of squeezed branch pile based on quadratic trend curve[J].Science Technology and Engineering,2009,9(14):4230-4233.
[10]李军亮.基于广义灰色模型的极限承载力建模与预测研究[D].武汉:武汉理工大学,2009.LI Jun-liang.Study on modeling and prediction of the ultimate bearing capacity based on the generalized gray model[D].Wuhan:Wuhan University of Technology,2009.
[11]刘思思,赵明华,李亮.基于锚杆抗拔试验的动态折线模型分析[J].岩土力学,2014,35(12):3389-3395.LIU Si-si,ZHAO Ming-hua,LI Liang.Analysis of dynamic broken line model based on experimental data of anchor anti-pullout[J].Rock and Soil Mechanics,2014,35(12):3389-3395.
[12]张昌锁,李义,ZOU Steve.锚杆锚固体系中的固结波速研究[J].岩石力学与工程学报,2009,28(增刊2):3604-3608.ZHANG Chang-suo,LI Yi,ZOU STEVE.Research on consolidation wave in grouted rock bolt structure system[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(Supp.2):3604-3608.
[13]王猛,李义,董嘉.应力波法锚杆锚固质量无损检测现场实验研究[J].煤炭技术,2013,32(1):203-204.WANG Meng,LI Yi,DONG Jia.Stress wave nondestructive testing method of rock bolt and field experimental study[J].Coal Technology,2013,32(1):203-204.
[14]张胜利,张昌锁,王银涛.锚杆锚固质量无损检测方法分析[J].煤矿安全,2014,45(5):212-215.ZHANG Sheng-li,ZHANG Chang-suo,WANG Yin-tao.Analysis of nondestructive detection method of bolt anchoring quality[J].Coal Safety,2014,45(5):212-215.
[15]宋伟,李枝文,肖柏勋,等.锚杆锚固质量无损检测数据的处理方法研究[J].工程地球物理学报,2012,9(3):337-341.SONG Wei,LI Zhi-wen,XIAO Bo-xun,et al.Research on signal processing of nondestructive testing data for anchorage quality of rock bolts[J].Chinese Journal of Engineering Geophysics,2012,9(3):337-341.
[16]STARKEY A,IVANOVlC A,RODGER A A,et al.Condition monitoring of ground anchorage by dynamic impulse:Granit system[J].Meccauica,2003,38:265-282.
[17]VRKLJAN I,SZAVITS NOSSAN A,KOVACEVIC M S.Nondestructive method for testing grouting quality of rock bolt anchors[C]//International Congress on Rock Mechanics.Rotterdam:A.A.Balkema Publish,1999:1475-1478
[18]中冶集团建筑研究总院.CECS 22-2005 岩土锚杆(索)技术规程[S].北京:中国计划出版社,2005.Central Research Institute of Building &Construction,China Metallurgical Construction Group Corporation.Republic of China CECS 22-2005 Technical specification for ground anchors[S].Beijing:China Planning Press,2005.
[19]夏阳,陆余良.D-S 证据推理及算法实现[J].安徽大学学报(自然科学版),2004,28(6):20-25.XIA Yang,LU Yu-liang.The application of D-S evidence theory and algorithm implementation[J].Journal ofAnhui University,Natural Science Edition,2004,28(6):20-25.
[20]孙晓云,张涛,王明明,等.基于改进指-幂混合函数模型的锚杆承载力预测方法研究[J].岩石力学与工程学报,2015,34(8):1641-1649.SUN Xiao-yun,ZHANG Tao,WANG Ming-ming,et al.A revised model for predicting the bearing capacity of rock bolts based on mixed exponential and power function[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(8):1641-1649.
[21]孙晓云,张涛,王振东,等.基于改进灰色GM(1,1)模型的锚杆承载力的预测方法[J].河北师范大学学报(自然科学版),2014,38(6):589-595.SUN Xiao-yun,ZHANG Tao,WANG Zhen-dong,et al.Study on the prediction method of ultimate resistance capacity of rock bolt based on the improved gray GM(1,1)model[J].Journal of Hebei Normal University(Natural Science Edition),2014,38(6):589-595.
[22]YANG J B,SING M G.An evidential reasoning approach for multiple-attributed decision making with uncertainty[J].IEEE Transaction on System,Man and Gybernetics,1994,24(1):1-18.
[23]马国清,赵亮,李鹏.基于Dempster-Shafer证据推理的多传感器信息融合技术及应用[J].现代电子技术,2003,(19):41-44.MA Guo-qing,ZHAO Liang,LI Peng.Mult-sensor information fusion theory based on dempster-shafer evidential reasoning and its application[J].Modern Electronics Technique,2003,(19):41-44.
[24]党宏社,韩崇昭,王立琦,等.基于模糊推理原理的多传感器数据融合方法[J].仪器仪表学报,2004,25(4):527-530.DANG Hong-she,HAN Chong-zhao,WANG Li-qi,et al.A multi-sensor data fusion method based on fuzzy logic reasoning[J].Chinese Journal of Scientific Instrument,2004,25(4):527-530.
[25]王贤能,叶蓉,周逢君.土层抗浮锚杆试验破坏标准选取的建议[J].地质灾害与环境保护,2001,(3):73-77.WANG Xian-neng,YE Rong,ZHOU Feng-jun.Proposals for the selection of failure criteria in soil float-resisting anchor rod test[J].Journal of Geological Hazards and Environment Preservation,2001,(3):73-77.
