Phase stability,elastic properties and electronic structures of Mg-Y intermetallics from frst-principles calculations

**J.Chen,K.TngM.P.Peng

aKey Laboratory of Lightweight and Reliability Technology for Engineering Vehicle,The Education Department of Hunan Province,Changsha University of Science and Technology,Changsha 410114,China

bKey Laboratory of Effcient and Clean Energy Utilization,College of Hunan Province,Changsha University of Science and Technology,Changsha 410114,China

cCollege of Materials Science and Engineering,Hunan University,Changsha 410082,China

Phase stability,elastic properties and electronic structures of Mg-Y intermetallics from frst-principles calculations

J.Zhanga,b,*,C.Maoa,*,C.G.Longa,J.Chenb,K.Tanga,M.J.Zhanga,P.Pengc

aKey Laboratory of Lightweight and Reliability Technology for Engineering Vehicle,The Education Department of Hunan Province,Changsha University of Science and Technology,Changsha 410114,China

bKey Laboratory of Effcient and Clean Energy Utilization,College of Hunan Province,Changsha University of Science and Technology,Changsha 410114,China

cCollege of Materials Science and Engineering,Hunan University,Changsha 410082,China

The phase stability,elastic properties and electronic structures of three typical Mg-Y intermetallics including Mg24Y5,Mg2Y and MgY are systematically investigated using frst-principles calculations based on density functional theory.The optimized structural parameters including lattice constants and atomic coordinates are in good agreement with experimental values.The calculated cohesive energies and formation enthalpies show that either phase stability or alloying ability of the three intermetallics is gradually enhanced with increasing Y content.The single-crystal elastic constantsCijof Mg-Y intermetallics are also calculated,and the bulk modulusB,shear modulusG,Young's modulusE, Poisson ratiovand anisotropy factorAof polycrystalline materials are derived.It is suggested that the resistances to volume and shear deformation as well as the stiffness of the three intermetallics are raised with increasing Y content.Besides,these intermetallics all exhibit ductile characteristics,and they are isotropic in compression but anisotropic to a certain degree in shear and stiffness.Comparatively,Mg24Y5presents a relatively higher ductility,while MgY has a relatively stronger anisotropy in shear and stiffness.Further analysis of electronic structures indicates that the phase stability of Mg-Y intermetallics is closely related with their bonding electrons numbers below Fermi level. Namely,the more bonding electrons number below Fermi level corresponds to the higher structural stability of Mg-Y intermetallics.

Magnesium alloys;Intermetallics;Phase stability;Elastic properties;Electronic structure

1.Introduction

Magnesium alloys have been attracted extensive attention and gained increasing applications in transportation felds due to their low density,high specifc strength and good stiffness. However,the widespread uses of magnesium alloys still remain obstacle fortheir low creep resistance,poorcorrosionresistance and poor deformation ability[1].In order to improve the comprehensive properties of magnesium alloys,many experimental attempts have been performed and some signifcant progresses have been achieved in recent decades.It was shown that magnesium alloys added with rare earth(RE)elements exhibit higher mechanical properties, better thermal stability and corrosion properties as well as improved deformability[2-5].

The yttrium(Y)is one typical representation of RE elements,which has been reported as an effective alloyingaddition to prepare high performance Mg-RE based alloys [6-8].It is known from Mg-Y phase diagram that Y possesses a high solid solubility in Mg of 12.5wt.%,which induces the remarkable solution strengthening effects. Additionally,Mg-Y alloys have three different intermetallic phases across different temperature ranges with increasing content of Y,i.e.Mg24Y5,Mg2Y and MgY[9].These intermetallics exhibit precipitate strengthening effects during decomposition of Mg-Y supersaturated solid solutions.Both solution and precipitate strengthening result in the enhanced mechanical properties and thermal stability of Mg-Y based alloys.Also the addition of Y element to magnesium alloys can lead to high corrosion resistance and deformability.The improved corrosion properties are mainly attributed to the formation of stable anti-oxide layer containing Y element on the surface of alloys[10].The enhanced deformability is mainly originated from the contribution of Y element on texture weakening[11].

Evidently,Y element plays important roles in improving the comprehensive performances of magnesium alloys.The investigations on Mg-Y based alloys are very important, especially for studying the effects of Y element on the properties of magnesium alloys.To data,although some experimental studies associated with Mg-Y based alloys have been performed[10-13],the systematic studies on the physical characteristics such as phase stability,elastic properties and electronic structures of Mg-Y intermetallics are scare due to the diffculties of experimental measurements.Considering the important roles of Mg-Y intermetallics in mechanical properties and thermal stability of magnesium alloys,their physical properties mentioned above should be thoroughly investigated and discussed.In this paper,a systematic study on the stability,elastic and electronic properties of Mg24Y5, Mg2Y and MgY intermetallics in Mg-Y based alloys is performed using frst-principles calculations based on density functional theory(DFT).The results will allow for providing usefuldata forunderstanding these intermetallicsand designing the high performance Mg-Y based alloys.

2.Calculation models and methodology

Mg24Y5phase is a cubic compound with space groupI-43m(No.217)andcI58 symmetry[14].Its unit cell contains 2 formula units as shown in Fig.1a.The lattice constants area=b=c=11.257 Å.There are two kinds of unequivalent Mg(Mg1 and Mg2)and Y(Y1 and Y2)atoms in Mg24Y5unit cell.The Mg1,Mg2,Y1 and Y2 atoms are located on the 24g,24g,2aand 8csites,respectively.Mg2Y phase is a hexagonal compound with space groupP63/mmc(No.194) andhP12 symmetry[14].Its unit cell contains 4 formula units as shown in Fig.1b.The lattice constants area=b=6.037 Å andc=9.752 Å.There are also two kinds of unequivalent Mg(Mg1 and Mg2)atoms but one kind of Y atoms in Mg2Yunit cell.The Mg1,Mg2 and Yare located on the 2a,6hand 4fsites,respectively.Similar to Mg24Y5,MgY phase is also a cubic compound with space groupPm-3m(No.221)andcP2 symmetry[14].Its unit cell contains 1 formula unit as shown in Fig.1c.The lattice constants area=b=c=3.796 Å.There is one kind of Mg and Yatoms in MgY unit cell.The Mg and Y atoms occupy the 1aand 1bsites,respectively.

The calculations are performed using a frst-principles plane-wave pseudopotential method based on density functional theory(DFT)[15].Ultrasoft pseudopotentials[16]in reciprocal space are used.The orbitals of Mg 2p63s2and Y 4s24p64d15 s2are treated as valence electrons.The Perdew-Wang(PW91)generalized gradient approximation(GGA) [17]is adopted for the exchange-correction functional.The cutoff energy of plane wave basis is set as 310 eV for all phases.The special points sampling integration over the brillouin zone is employed by using the Monkhorst-Pack method [18]with 2×2×2,4×4×2 and 6×6×6 specialk-point meshes for Mg24Y5,Mg2Y and MgY phases,respectively.A fnite basis set correction and the Pulay scheme of density mixing[19,20]are applied for evaluation of energy and stress. The cell parameters including lattice constants and atomic coordinates of all phases are fully relaxed according to the total energy and force using the Broyden-Flecher-Goldfarb-Shanno(BFGS)scheme[21]based on the convergence criteria of optimization(energy of 2.0×10-5eV/atom,force of 0.05 eV/Å,stress of 0.1 GPa and displacement of 0.002 Å). The calculations of single-point energy,elastic properties and electronic structures are followed by cell optimization.By increasing the cutoff energy of plane wave to 380 eV and the k-point meshes to 3×3×3,5×5×4 and 8×8×8 for Mg24Y5,Mg2Yand MgY phases,respectively,their respective total energies and lattice constants are changed by less than 0.02 eV/atom and 0.09%,respectively.Therefore,the present calculations are precise enough to represent the ground-state properties of these intermetallics.

3.Results and discussions

3.1.Structural properties

Starting from experimentally available structural parameters,the lattice constants and atomic coordinates of Mg24Y5, Mg2Yand MgY phases are estimated from the minimized total energy with breaking their symmetries.The calculated results are listed in Table 1.It is found that the optimized structures of three phases retain their respective space groups.The equilibrium lattice constants of crystal cells and atomic coordinates are also consistent with experimental values[14]. The maximal deviation of lattice constants calculated here relative to the experimental results is only 0.58%(avalue of Mg2Y),suggesting that the calculations in the present work are highly reliable.

In general,the structural stability of crystal is closely associated with its cohesive energy.A higher cohesive energy indicates the crystal combines frmly and is uneasy to decompose.In other words,the stability is good[22].In order to understand the structural stabilities of Mg-Yintermetallics, their cohesive energiesEcohare calculated using Equation(1) [22]:

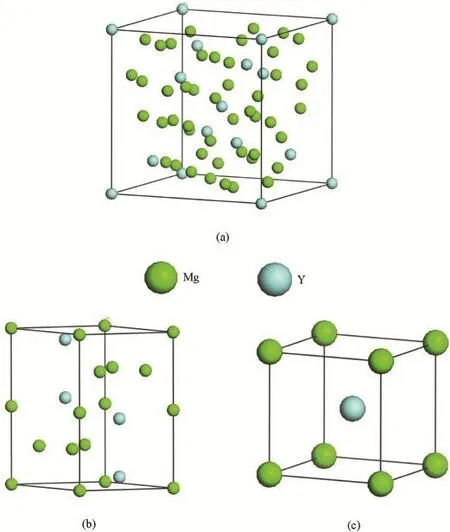
Fig.1.The crystal cell models of Mg24Y5(a),Mg2Y(b)and MgY(c)intermetallics.

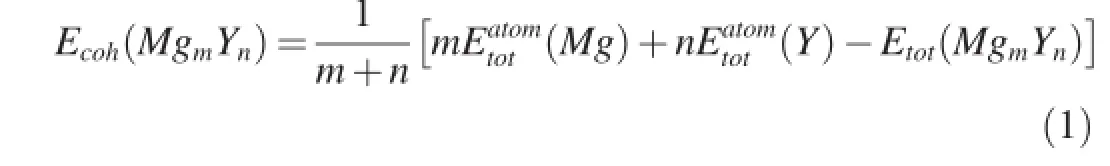
whereEtot（MgmYn）represents the total energies per formula unit of MgmYn(Mg24Y5,Mg2Y and MgY)intermetallics.（Mg）and（Y）represent the total energies of single Mg and Y atoms in free state,respectively.The subscriptsmandnrepresent the atomic numbers of Mg and Y within MgmYncrystal cells,respectively.The calculated results ofEcohare plotted as shown in Fig.2.It can be found that theEcohvalues of the three intermetallics increase in the order ofMg24Y5,Mg2Y and MgY.This means that the structural stabilities of Mg-Y intermetallics are enhanced with increasing Y content.

Table 1The calculated lattice constants(in Ǻ)and atomic coordinates of Mg24Y5,Mg2Y and MgY intermetallics.

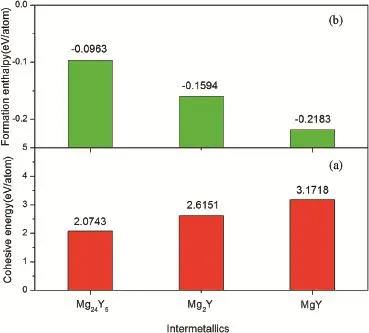
Fig.2.The calculated cohesive energies(a)and formation enthalpies(b)of Mg24Y5,Mg2Y and MgY intermetallics.

Besides,the alloying ability of crystal can be evaluated by its formation enthalpy.Commonly,a negative formation enthalpy means crystal can be formed and exist stably. Furthermore,a lower formation enthalpy corresponds to a stronger alloying ability of crystal[23].In order to assess the alloying abilities of Mg-Y intermetallics,their formation enthalpies ΔHformare further calculated using Equation(2) [23]:

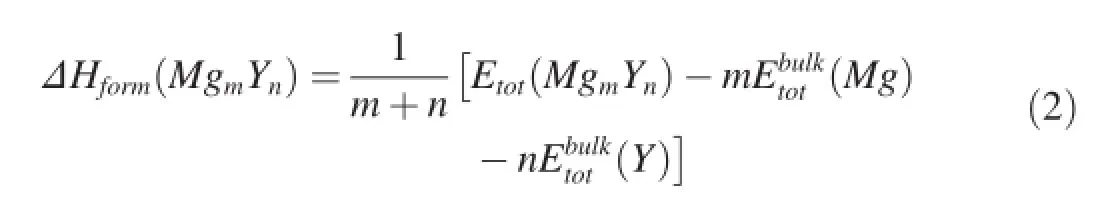
3.2.Mechanical properties

The elastic constants determine the response of a crystal to external forces,as characterized by bulk modulus,shear modulus,Young's modulus,and Poisson's ratio,and obviously play an important part in determining the mechanical properties of the materials[24].Therefore,it is essential to investigate the elastic constants to understand the mechanical properties of Mg-Y intermetallics.A stress-strain approach is employed to calculate elastic properties in the present work [25].According to the generalized Hook's law,a linear relationship exists between stress(σ)and strain(ε).Thus,proportional elastic constantCijcan be written as Equation(3):

In order to obtain each independent elastic constant,an appropriate number of strain patterns are imposed on crystal cell with a maximum strain value of 0.003 in the present calculations.The calculated independentCijvalues of the three Mg-Y intermetallics are listed in Table 2.For Mg24Y5and MgY with cubic structure as well as Mg2Y with hexagonal structure,their mechanical stability criteria can be expressed as Equations(4)and(5)respectively:

Cubic structure[26]:

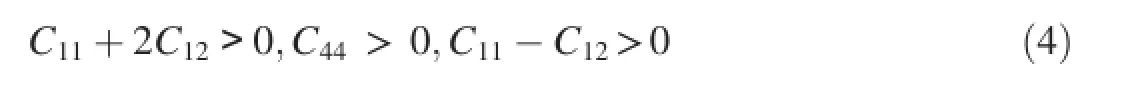
Hexagonal structure[26]:

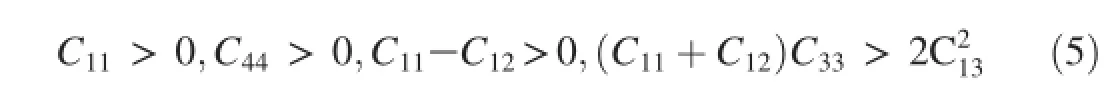
From Table 2,it can be derived that the calculated elastic constants satisfy the above corresponding criteria,indicating the mechanical stability of Mg-Y intermetallics.

Based on the independent single-crystal elastic constants of Mg-Y intermetallics,their bulk modulus(B),shear modulus (G),Young's modulus(E)and Poisson's ratio(v)for polycrystalline crystal can be deduced.For all crystal structures, the polycrystalline modulus can be estimated by two approximation methods,i.e.the Voigt and Reuss methods[27],and they can be expressed as Equations(6)-(9):

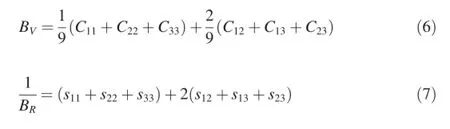
Table 2The calculated elastic constants(Cij)(in GPa)of single-crystal Mg24Y5,Mg2Y and MgY intermetallics.

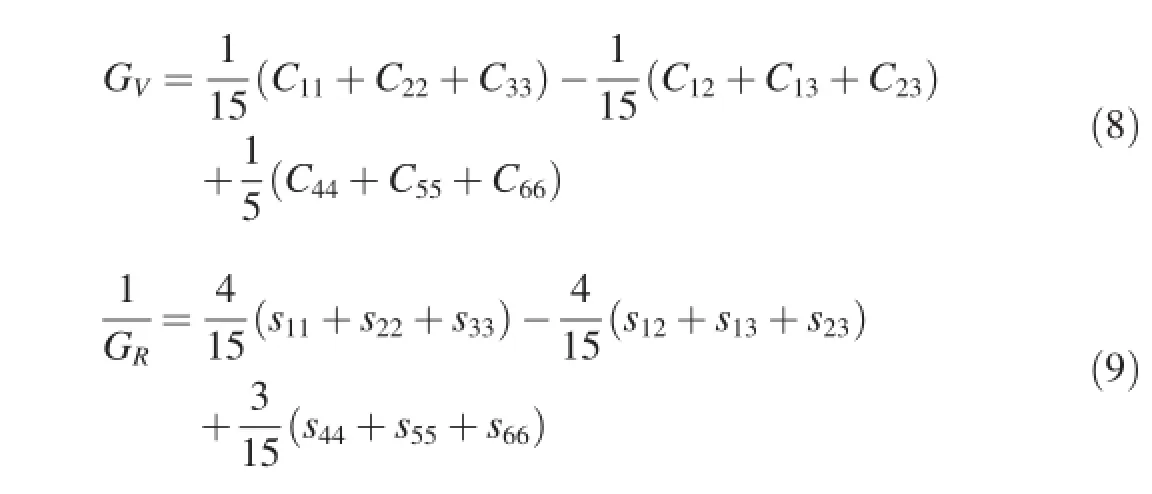
whereSijare the elastic compliance constants.VandRrepresent the Voigt and Reuss bounds.They provide the maximum(Voigt)and minimum(Reuss)limits of the polycrystalline elastic modulus.The average of the voigt and Reuss bounds are Voigt-Reuss-Hill(VRH)average[27],which is considered as the best estimate of the theoretical polycrystalline elastic modulus.They can be expressed as Equations(10)and(11)respectively:

Additionally,the Young's modulus(E)and Poisson's ratio (v)can also be calculated from the bulk modulus(B)and shear modulus(G)using Equations(12)and(13)[25]respectively:

The calculated results are listed in Table 3.Commonly,the bulk modulus is assumed to be a measure of resistance to volume change by applied pressure[28].A larger bulk modulus corresponds to a stronger resistance to volume change by applied pressure.Additionally,the shear modulus is an indication of resistance to reversible deformations upon shear stress[28].A larger shear modulus corresponds to a more notable directional bonding between atoms.From Table 3,it is seen that eitherBVRHorGVRHvalues of the three intermetallics increase in the order of Mg24Y5,Mg2Y and MgY, suggesting that the resistances to volume and shear deformation of Mg-Y intermetallics are enhanced with increasing Y content.Furthermore,the Young's modulus is assumed to be a measure of stiffness of materials[28].A larger Young's modulus corresponds to a stiffer material.Obviously,the stiffness of the three Mg-Y intermetallics is also raised with increasing Y content.

The quotient of shear modulus to bulk modulus,i.e.G/B,of crystalline phases proposed by Pugh[28]can be considered as an indication of the extent of fracture range in materials. According to the Pugh criterion,a high or lowG/Bvalue is associated with brittleness or ductility.Commonly,a material is regarded as brittle ifG/Bvalue is above 0.57,and vice versa. From Table 3,the values of the three Mg-Y intermetallics are all less than 0.57,suggesting they are all ductile.Comparatively,Mg24Y5phase exhibits the biggest ductility.Besides, the Poisson's ratio can refect the stability of a crystal against shear,which usually ranges from-1 to 0.5[28].The smaller value of Poisson's ratio corresponds to the more stable against shear of crystal.The calculated results in Table 3 show that the three Mg-Y intermetallics are all unstable against shear owing to their close values to 0.5.Comparatively,Mg24Y5phase presents the best plasticity,which keeps consistent with the analytical result fromG/B.

Elastic anisotropy of crystals refects a different bonding character in different directions and has an important implication since it correlates with the possibility to induce microcrack in materials.Chung and Buessem introduced a concept of percent elastic anisotropy which is a measure of elastic anisotropy possessed by the crystal under consideration [24].The percentage anisotropy in compression,shear and stiffness are defned as Equations(14)-(16)respectively:

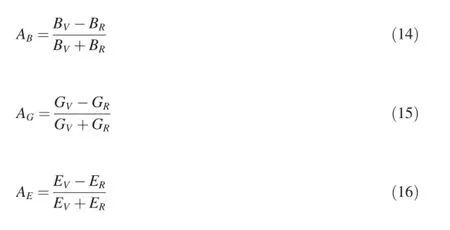
whereB,GandEare the bulk,shear and Young's modulus, respectively.The subscriptsVandRrepresent the Voigt and Reuss bounds.For the three expressions,a value of zero represents elastic isotropy and a value of 1(100%)is the largest possible anisotropy.The calculated anisotropy factors ofAB,AGandAEare also listed in Table 3.Clearly,the three Mg-Y intermetallics nearly exhibit isotropy in compression,but present anisotropy to a certain degree in shear and stiffness. Comparatively,MgY phase has a relatively strong anisotropy in shear and stiffness.

3.3.Electronic structures

To reveal the nature of bonding interactions within Mg-Y intermetallics and understand their structural stability mechanism,the total and partial density of states per atom of Mg24Y5,Mg2Y and MgY are calculated and compared as shown in Fig.3.In these fgures,the Fermi level(EF)is set as zero and used as a reference.From Fig.3(a)-(c),it can be found that the three Mg-Y intermetallics all exhibit metallic properties.Their bonding peaks are mainly located in energy region fromEFto-7 eV,and mainly originate from the contribution of valence electron numbers of Y(4s),Y(5s), Y(4p),Y(4d),Mg(3s)and Mg(2p)orbits.Further comparison of total densities of states of the three Mg-Y intermetallics per atom is performed as shown in Fig.3d.The bonding electrons numbers of these intermetallics are calculated by integrating the total densities of states belowEF,and the calculated values are 2.1656,2.3202 and 2.4274electrons/atom for Mg24Y5,Mg2Y and MgY respectively.Commonly,the bonding electrons number belowEFcan be used to characterize and judge the structural stability of crystal,the more bonding electrons number belowEFmeans the higher structural stability of crystal[29].Therefore,the sequence of structural stability for the three Mg-Y intermetallics is: MgY＞Mg2Y＞Mg24Y5,which is consistent with the results from energetic point of view.

4.Conclusions

Using frst-principles calculations method based on density functional theory(DFT),the phase stability,elastic properties and electronic structures of Mg-Y intermetallics including Mg24Y5,Mg2Y and MgY are systematically investigated.The main conclusions are summarized as the following:

1)Either phase stability or alloying ability of Mg-Y intermetallics is gradually enhanced with increasing Y content.

2)The resistances to volume and shear deformation as well as the stiffness of Mg-Y intermetallics are enhanced with increasing Y content.

3)Mg-Y intermetallics all exhibit ductile characteristics, and they are isotropic in compression but anisotropic to a certain degree in shear and stiffness.Comparatively,Mg24Y5presents a relatively higher ductility,while MgY phase has a relatively strong anisotropy in shear and stiffness.

4)The phase stability of Mg-Y intermetallics is closely related with their bonding electrons numbers below Fermi level.The more bonding electrons number below Fermi level corresponds to the higher structural stability of Mg-Y intermetallics.

Acknowledgments

This work was fnancially supported by the National Natural Science Foundation of China(No.51401036),the Hunan ProvincialNaturalScience Foundation ofChina (No. 14JJ3086),the Research Foundation of Education Bureau of Hunan Province(No.12B001)and the Key Laboratory of Effcient and Clean Energy Utilization,College of Hunan Province(No.2015NGQ005).

[1]H.E.Friedrich,B.L.Mordike,Magnesium Technology(Metallurgy, Design Data,Applications),Springer,Berlin,2006.

[2]Y.D.Wang,G.H.Wu,W.C.Liu,S.Pang,Y.Zhang,W.J.Ding,Mater. Sci.Eng.A 594(2014)52-61.

[3]L.Li,J.Alloys Comp 555(2013)255-262.

[4]G.Ben-Hamu,D.Eliezer,K.S.Shin,S.Cohen,J.Alloys Comp.431 (2007)269-276.

[5]J.E.Saal,C.Wolverton,Acta Mater.68(2014)325-338.

[6]A.D.Sudholz,K.Gusieva,X.B.Chen,B.C.Muddle,M.A.Gibson, N.Birbilis,Corro.Sci.53(2011)2277-2282.

[7]D.L.Zhang,B.L.Zheng,Y.Z.Zhou,S.Mahajan,E.J.Lavernia,Scr. Mater.76(2014)61-64.

[8]S.Sandl¨obes,M.Fri′ak,J.Neugebauer,D.Raabe,Mater.Sci.Eng.A 576 (2013)61-68.

[9]L.L.Rokhlin,Magnesium Alloys Containing Rare Earth Metals,Taylor&Francis,London,UK,2003.

[10]H.Ardelean,A.Seyeux,S.Zanna,Corro.Sci.73(2013)196-207.

[11]L.B.Tong,X.H.Li,J.Zhang,Mater.Sci.Eng.A 563(2013)177-183.

[12]R.Cottam,J.Robson,G.Lorimer,B.Davis,Mater.Sci.Eng.A 485 (2008)375-382.

[13]C.Zlotea,M.Sahlberg,P.Moretto,Y.Andersson,J.Alloys Comp.489 (2010)375-378.

[14]P.Villars,L.D.Calvert,Pearson's Handbook of Crystallographic Data for Intermetallic Phases,ASM,Metals Park,Ohio,1985.

[15]M.D.Segall,L.D.Lindanp,M.J.Probert,C.J.Pickard,P.J.Hasnip, S.J.Clark,M.C.Payne,J.Phys.Condens.Matter 14(2002)2717-2744.

[16]D.Vanderbilt,Phys.Rev.B 41(1990)7892-7895.

[17]J.P.Perdew,K.Burke,M.Ernzerhof,Phys.Rev.Lett.77(1996)3865-3868.

[18]H.J.Monkhorst,J.D.Pack,Phys.Rev.B 13(1976)5188-5192.

[19]B.Hammer,L.B.Hansen,J.K.Nørskov,Phys.Rev.B 59(1999) 7413-7421.

[20]G.P.Francis,M.C.Payne,J.Phys,Condens.Matter 2(1990)4395-4404.

[21]T.Fischer,J.Almlof,J.Phys.Chem.96(1992)9768-9774.

[22]Y.K.Han,J.Jung,J.Chem.Phys.121(2004)8500-8502.

[23]N.A.Zarkevich,T.L.Tan,D.D.Johnson,Phys.Rev.B 75(2007)104203.

[24]P.Ravindran,L.Fast,P.A.Korzhavyi,B.Johansson,J.Wills, O.Eriksson,J.Appl.Phys.84(1998)4891.

[25]W.Zhou,L.J.Liu,B.L.Li,P.Wu,Q.G.Song,Comp.Mater.Sci.46 (2009)921-931.

[26]D.C.Wallace,Thermodynamics of Crystals,Wiley,New York,1972.

[27]J.H.Westbrook,R.L.Fleischer,Basic Mechanical Properties and Lattice Defects of Intermetallic Compounds,Wiley,New York,2000.

[28]M.M.Wu,L.Wen,B.Y.Tang,L.M.Peng,W.J.Ding,J.Alloys Comp. 506(2010)412-417.

[29]J.Nyl′en,F.J.Garcìa,B.D.Mosel,R.P¨ottgen,U.H¨aussermann,Solid State Sci.6(2004)147-155.

Received 10 December 2014;revised 25 January 2015;accepted 17 March 2015 Available online 16 May 2015

*Corresponding authors.Key Laboratory of Lightweight and Reliability Technology for Engineering Vehicle,The Education Department of Hunan Province,Changsha University of Science and Technology,Changsha 410114, China.Tel./fax:+86 731 85258646.

E-mail addresses:zj4343@163.com(J.Zhang),1305648099@qq.com(C. Mao).

Peer review under responsibility of National Engineering Research Center for Magnesium Alloys of China,Chongqing University.

http://dx.doi.org/10.1016/j.jma.2015.03.003.

2213-9567/Copyright 2015,National Engineering Research Center for Magnesium Alloys of China,Chongqing University.Production and hosting by Elsevier B.V.All rights reserved.

Copyright 2015,National Engineering Research Center for Magnesium Alloys of China,Chongqing University.Production and hosting by Elsevier B.V.All rights reserved.