基于线性嵌套的舱位控制研究

朱文丽，徐月芳，黄 玉

(南京航空航天大学 民航学院，江苏 南京 211106)



基于线性嵌套的舱位控制研究

朱文丽，徐月芳，黄 玉

(南京航空航天大学 民航学院，江苏 南京 211106)

航空公司的舱位控制作为收益管理的核心，已经受到了越来越多的关注。分析了是否考虑舱位嵌套对高等级舱位的座位保护水平的影响，建立了两种情况下的数学模型，利用拉格朗日乘子法求得高等级舱位座位保护水平的最优解。结果证明，在舱位嵌套下，高等级座位保护水平显著降低。将模型运用到实例中，数据显示该模型可以给出更优的各等级舱位保护水平，提高航空公司收益，避免舱位虚耗。

航空公司;舱位嵌套;静态控制;座位保护水平

在过去的20年间，我国航空运输业保持了年均13.2%的快速增长。旅客运输量从2006年的1.6亿人次增长到2014年的3.9亿人次，预计在2015年可以达到4.3亿人次。但目前由于中高端客源锐减，表明航空稳定需求的商务旅客出现持续下滑，解决航空公司如何提高收益的问题迫在眉睫。舱位控制问题作为收益管理的核心，将不同价格水平的商品划分为不同的数量，合理安排各舱位等级的数量，减少收益稀释，达到收益最大化。

最早关于舱位控制的研究是1987年BELOBABA[1]的期望边际座位收益理论，高强等[2]将旅客始-终点流按票价由高到低排序，定义旅客始-终点流为决策变量，以各始-终点流需求为约束条件，以航线期望总收益为目标函数，建立了多航段舱位控制问题的随机规划模型。董裴君[3]引入影子价格，拓展了期望边际座位收益方法，并针对中枢辐射网络的舱位控制问题，提出了网络贡献值模型。樊玮等[4]从旅客选择的角度，通过对旅客偏好和效用的分析，选取离散选择模型，构建了非齐次旅客到达的动态舱位控制算法。陈蓉[5]在研究旅客选择行为及旅客市场细分的基础上，构建了市场细分条件下旅客选择舱位控制模型，利用Logit模型进行旅客行为模拟，同时进行EMSRb算法仿真，结果表明旅客选择模型的收益优于传统的EMSRb模型。ANDRISMÖLLER等[6]用多级随机规划方法确定航空公司网络全航段多票价等级的座位保护水平，提出场景树的方法处理多维和多元随机过程。NICHOLAS等[7]用自适应随机存量控制对航空公司舱位控制进行了动态优化，通过有条件的次序统计量的可预测性，决定接受或拒绝任何客户要求，建立基于当前的累积客户次序统计的需求决策规则。罗利等[8]应用随机控制理论和博弈理论，建立了竞争市场环境下两家航空公司的两个航班两级价格动态定价连续时间数学模型。李晓花[9]利用最大凹向包络原理构建了航空公司客运收入管理的动态定价与舱位控制的优化模型，并提出“确定最优价格集、确定开放舱位数、确定最优价格”的决策三阶段。CHEN[10]基于消费者偏好的概念提出了基于启发式算法的分配优化模型。郭晖[11]引入社会阶层理论，建立了二层架构特征的区域航空市场旅客分层模型，并给出了适应区域航空市场客源分布特征的区域航空公司定价管理策略和存量管理策略。

上述研究的不足是没有考虑在实际舱位控制过程中，航空公司会根据航班的各个舱位需求设定可售配额数，确保低舱位有座位，高舱位也有座位开放销售，舱位间使用NESTING，即舱位嵌套，高舱位数量不足时，会自动向低舱位借位。因此笔者重点给出了舱位嵌套下如何根据旅客需求确定各舱位的座位保护水平的方法。

1 舱位嵌套问题

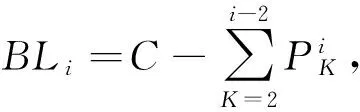
图1 多等级子舱嵌套式舱位分配图

以东方航空公司为例，表1为东方航空公司A320及A321的初始舱位设置表。F代表头等舱，P代表头等舱子舱，A代表里程积分兑换的头等舱，其余依次为经济舱全价，以及9.5折，9折，8.5折，以此类推。经济舱全价属于全部开放状态。高舱位自动向低舱位借舱。例如E舱位代

表1 东方航空公司A320及A321的初始舱位设置表

表8.5折，当前处于开放状态，E舱本身的座位保护水平为5个，但最大可售舱位共77个。

2 舱位控制模型

2.1 条件假设与符号说明

该研究基于以下假设条件：航班是单航节航班，分为高票价和低票价两个舱位等级；旅客需求随机分布并相互独立；低票价旅客需求先于高票价旅客的需求，默认最先到达是最低票价的需求；不考虑超售、No-show、取消订座等情况；舱位线性嵌套。

符号说明：Y1代表高舱位需求，μ1代表高舱位座位保护水平，c1代表高舱位价格；Y2代表低舱位需求，μ2代表低舱位座位保护水平，c2代表低舱位价格；fθj(yj)代表需求Yj在参数为θj下的概率密度函数；Pr{Y1>μ1}代表高票价需求大于高票价座位保护数的概率。

2.2 模型建立

在静态舱位控制中，笔者分两种情况给出了收益表达式。首先在不考虑舱位嵌套的情况下，单航节两舱的最大期望收益表达式为：

I1(μ1,μ2|θ1,θ2)=Eθ1{c1min(μ1,Y1)}+

Eθ2{c2min(μ2,Y2)}

(1)

μ1+μ2≤μ,μj≥0j=1,2

(2)

Eθj{cjmin(μj,Yj)}=cj[Eθj{Yj|Yj≤μj}·

Pr{Yj≤μj}+Eθj{Yj|Yj>μj}Pr{Yj>μj}]=

(3)

用拉格朗日乘子法得到的最优解满足:

(4)

在考虑座位嵌套时，针对如何确定旅客的订座限制，建立两舱最大期望收益表达式，即：

I2(μ1,μ2|θ1,θ2)=

Eθ2{Eθ1{c1min(μ1+μ2-Y2,Y1)}}+

Eθ2{c2min(μ2,Y2)}

(5)

μ1+μ2≤μ,μj≥0j=1,2

(6)

Eθ2{Eθ1{c1min(μ1+μ2-Y2，Y1)}}=

(7)

使用拉格朗日乘子法得到的最优解满足：

c2/c1=Pr{Y1>μ1}

(8)

比较上述两种结果，由于Pr{Y2>(μ-μ1)}≤1，因此式(4)中μ1的结果较大，也就是为高票价旅客保留了更多的座位。实际上并没有必要预留这么多高票价座位，嵌套座位可以满足高票价旅客的需求，式(8)采取合适的座位保护水平可以提高航班的客座率，增加航空公司的收益。式(8)是基于完全信息下的静态舱位分配策略，Fθ是Y1在参数θ下的概率分布函数，当Fθ连续并严格单调递增时，式(8)等同于：

(9)

(10)

然而在实际情况中参数θ常常是未知的，因此笔者引入了最大似然估计量：

(11)

(12)

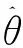
(13)

考虑式(9)及航班上的当前累计需求Y1,构建静态无偏订座策略:

k=1,2,…,m-1

(14)

(15)

3 实例验证

以南方航空公司从广州飞往昆明的CZ3407航班为例，该航班机型为A320，共有152个座位，分为经济舱和明珠公务舱。该航班经济舱全价为1 380元，分别有4折、5折、6折、7折、8折、9折、全价及3 200元的公务舱全价。假设旅客需求服从正态分布(μ,σ)，选取连续30天的CZ3407航班，根据各舱位销售情况确定各舱位需求预测，如表2所示。

表2 旅客需求预测

根据笔者建立的模型利用Matlab求解，确定各舱位的座位预留水平和最大订座限度，得到优化后的舱位控制结果,如表3所示。

表3 模型应用结果

在该舱位设置条件下，期望收益值可以达到121 590元，与实际历史数据的平均收益值114 220元相比，增加了7 370元利润，收益增长了6.45%。因此笔者提出的模型对各舱位座位保护水平有效地进行了优化，既满足了高端旅客的需求，还通过提高低等级座位的销售数量，增加了航空公司在该航班的收益。

4 结论

通过计算可以看出，嵌套舱位控制下的模型提高了航空公司的收益，该方法不仅理论上可行，在实际操作中也有一定意义。笔者提出的模型给出了在多等级舱位下，各等级舱位的座位保护水平。航空公司不仅不影响高票价旅客的订座，还通过合适的舱位设定赢得了更多低票价旅客，从而增加客座率，提高总收益。在未来的研究中，还可以考虑加入旅客的选择行为、退票超订等因素，结合旅客需求预测对舱位进行实时的动态控制。

[1] BELOBABA P P.Airline yield management an overview of seat inventory control[J].Transportation Science,1987(21):66-73.

[2] 高强，朱金福，陈可嘉.航空收益管理中多航段舱位控制方法研究[J].交通运输工程学报,2005,5(4):82-85.

[3] 董裴君.航空公司网络舱位控制方法研究[D].南京:南京航空航天大学,2007.

[4] 樊玮，刘向英.基于非齐次旅客到达选择的舱位控制比较研究[J]. 计算机技术与发展,2013(5):167-171.

[5] 陈蓉.基于旅客选择的航班座位优化分配模型[J]. 中国民航大学学报,2014(4):55-58.

[6] ANDRISMÖLLER R, KLAUS W.Airline network revenue management by multistage stochastic programming[J]. Computational Management Science,2008,5 (4):355-377.

[7] NICHOLAS N, MARIS P, ULDIS R,et al.Adaptive stochastic airline seat inventory control under parametric uncertainty[J].Lecture Notes in Computer Science, 2013(7894):308-323.

[8] 罗利，彭际华.竞争环境下的民航客运收益管理动态定价模型[J].系统工程理论与实践，2007(11):15-24.

[9] 李晓花.航空公司客运收入管理动态定价与舱位控制的统一策略及其风险分析初探[D].成都：四川大学,2004.

[10] CHEN L J.Mathematical programming models for revenue management under customer choice[J]. European Journal of Operational Research,2010(203):294-305.

[11] 郭晖.区域航空公司收益管理模型及其应用研究[D].武汉:华中科技大学,2008.

ZHU Wenli:Postgraduate; School of Civil Aviation, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China.

[编辑：王志全]

Seat Inventory Control under Linear Nesting

ZHUWenli,XUYuefang,HUANGYu

Airline seat inventory control is the core of revenue management. It has received more and more attentions. The difference whether nesting seat was taken into consideration was analyzed. And two mathematical models were constructed respectively. The optimal solution of high-glass seat protection level was obtained by Lagrange multiplier method. The result of a case proves that nesting seat allocation can achieve a significant lower protection level under seat nesting. The optimal solutions of each glass seat protection level could be given in the model. At the same time higher yield could be achieved by avoiding seat wasting.

airline; nesting seat; static control; seat protection level

2015-06-25.

朱文丽(1991-)，女，江苏镇江人，南京航空航天大学民航学院硕士研究生.

南京航空航天大学研究生创新基地(实验室)开放基金资助项目(kfjj20150704).

2095-3852(2015)06-0703-03

A

V214.1

10.3963/j.issn.2095-3852.2015.06.009