考虑预防性维修的二维延伸产品保证策略
2015-02-16刘子先
蒋 冉,刘子先
(天津大学 管理与经济学部,天津 300072)
考虑预防性维修的二维延伸产品保证策略
蒋 冉,刘子先
(天津大学 管理与经济学部,天津 300072)
针对产品保证服务成本持续上升的问题,将预防性维修与修正性维修有效集成,提出了考虑预防性维修的二维延伸产品保证策略,建立了以保证服务成本最小为目标的保证服务成本模型,并对不同使用率下的保证服务成本进行优化以确定最优的保证策略。采用数值分析方法将其与最小维修策略进行对比,结果显示保证服务成本有了显著的降低。
产品保证;预防性维修;保证服务成本模型;保证策略
随着竞争的加剧,对于像汽车这样的产品,产品保证条款越来越成为促进产品销售的重要因素,同时越来越多的制造商更加倾向于提供延伸产品保证为所售产品提供额外的保险。但是随着产品保证范围的不断扩大,产品发生失效的概率也随之递增,使得制造商根据保证策略为消费者提供保证服务的成本不断增加。由于预防性维修可以降低产品发生失效的概率并提高产品的可靠性,从而降低制造商的产品保证成本,因此笔者进行了考虑预防性维修的二维延伸产品保证策略研究。
目前,很多学者对考虑预防性维修的一维保证策略进行了深入研究,CHUN[1]首次将产品保证与维修策略联系起来,研究了免费保证及修正性保证下考虑预防性维修的最优保证更换策略。随后YEH等[2]研究了可修产品的预防性维修保证,在役龄回退维修计划下建立保证成本模型,通过有效的算法优化求解,指出存在唯一的最优预防性维修保证策略使得期望预防性维修保证成本最小。KIM等[3]分别从消费者及制造商的角度出发,设计出保修产品的预防性维修研究框架。CHANG等[4]则从制造商的角度提出当产品的寿命达到时间控制限时实施预防性维修的策略,以此确定可修产品的最优预防性维修策略及延长保证周期使得制造商总利润最大化。
随着研究的不断深入,已有不少学者对二维产品保证策略进行了研究,但是主要集中在二维基础产品保证策略研究。ISKANDAR等[5]首次将一维产品保证下的维修策略扩展到二维产品保证策略,其将产品保证区域分为两个不相交的子区域,提出在划分区域内发生的失效全部采用最小维修或者全部更换的策略。在此基础上ISKANDAR等[6]进行了扩展研究,其将二维免费维修产品保证区域划分为Ω1、Ω2和Ω3这3个不相交的子区域,每个子区域对于发生失效的部件都有相应维修度的维修策略,通过确定这些子区域的边界使得单位期望成本最小化。于俭等[7]则在类似的保证服务策略中考虑了不完全维修,即在保证区域内的特定区域首次失效采用不完全维修将其修复,而其他的故障则由最小维修将其修复。另外BANERJEE等[8]、JACK等[9]及于俭等[10]也进行了类似的研究。CHUKOVA等[11-12]则将保证区域划分为4个及n个子区域进行类似的研究。以上研究只是针对二维基础产品保证区域内没有考虑预防性维修的简单保证策略研究。目前关于二维延伸性产品保证下的维修策略的研究不多,主要有SHAHANAGHI等[13]对产品的失效模型进行了分析,在此基础上建立了考虑周期性不完全预防性维修的二维延伸产品保证服务成本模型,以最优的预防性维修策略使得期望保证服务成本最小化。SU等[14]研究了最小维修策略、最小不完全维修策略,以及最小完全维修策略的一维延长保证和二维延伸产品保证策略,指出二维延伸性产品保证要优于一维延长保证,最小维修方式适合较短的保证周期,而最小完全维修策略适用于长期保证。仝鹏等[15]研究了结合最小维修与不完全维修的二维汽车产品延伸产品保证策略。
笔者在文献[4]研究的基础上,提出将产品的寿命达到时间控制限时实施预防性维修的方法应用到二维延伸性产品保证策略的研究,根据该策略建立相应的产品保证服务成本模型,并进行相应的策略优化和成本数值分析。
1 模型构建
1.1 模型假设与数学符号
在构建数学模型前,提出以下基本假设:
(1)产品是广义的可修产品,产品的失效率在整个保证范围内随着时间及使用率递增;
(2)在基础保证期内的所有失效都采用最小维修方式进行修复;
(3)整个保证范围内不考虑更换方式;
(4)与产品的失效间隔时间相比,实施最小维修及预防性维修的时间可以忽略不计;
(5)二维延伸产品保证在基础保证结束后立即生效。
模型中所的数学符号及含义如表1所示。

表1 模型中的数学符号及含义
1.2 模型描述
1.2.1 失效模型
产品的失效是使用时间、使用程度等因素共同作用的结果,在二维产品保证下则主要考虑使用时间及使用程度对产品失效过程的影响。假设特定使用者的产品使用率R为常数,但不同使用者其使用率是不同的。使用率R可以看成是具有概率密度函数g(r),0≤r<∞(累计分布函数为G(r))的非负随机数。在R=r的条件下,使用程度μ是使用寿命t的线性函数,即μ=rt。
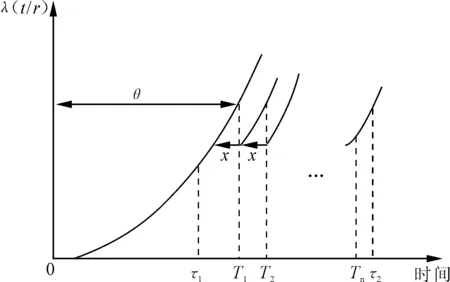
在这种情形下,失效函数则成为使用寿命t和使用率r的函数,即λ(t|r)。λ(t|r)δt则表示产品在t时刻运行,但是在[t,t+δt)内失效的概率。如果发生失效时采用最小维修方式,那么产品的失效过程为非齐次泊松过程。ISKANDAR等建议在R=r的条件下,λ(t|r)的形式为:
λ(t|r)=θ0+rθ1+(θ2+rθ3)t2
(1)
其中,确定性系数θi>0,0≤i≤3。
1.2.2 二维延伸性保证策略描述
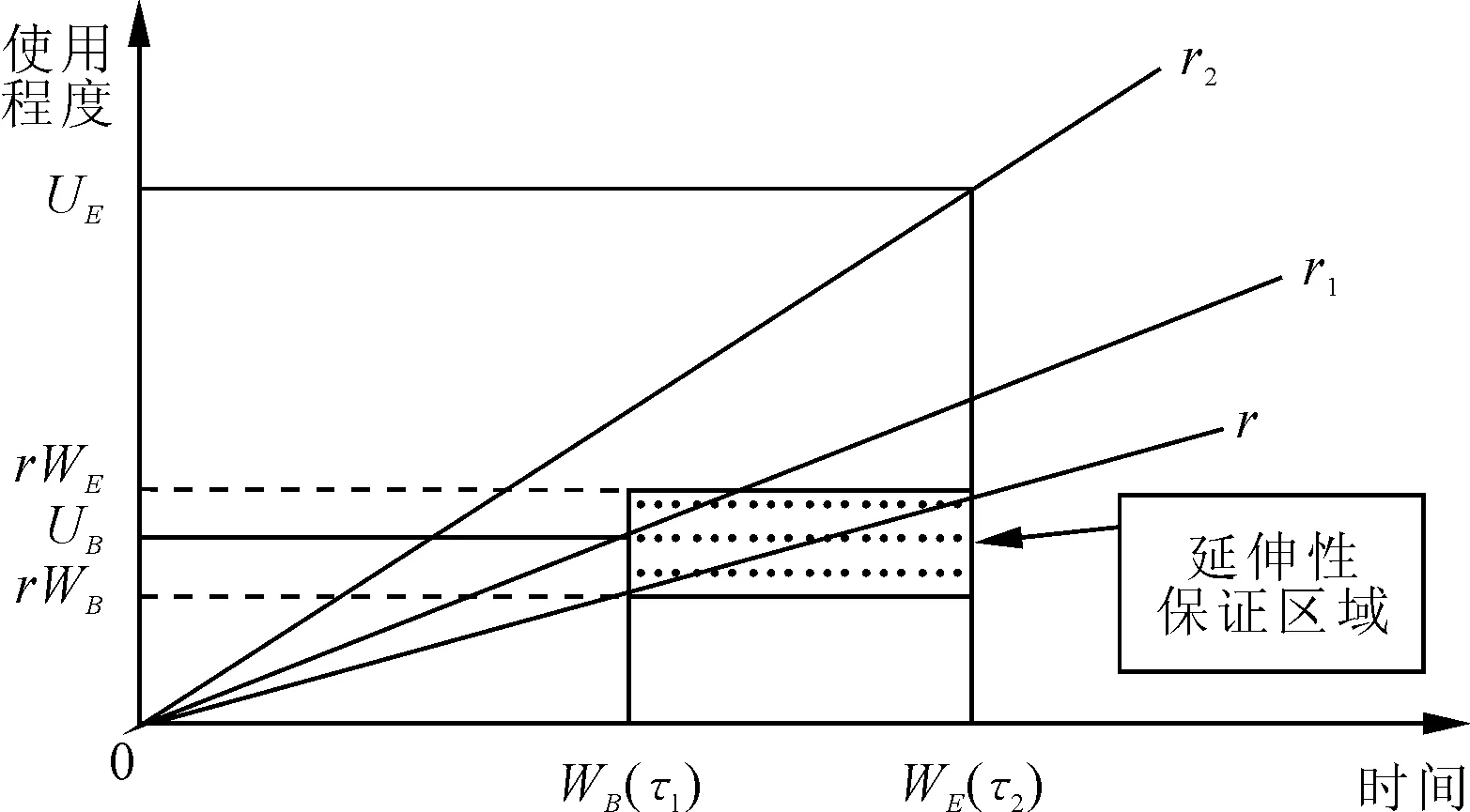
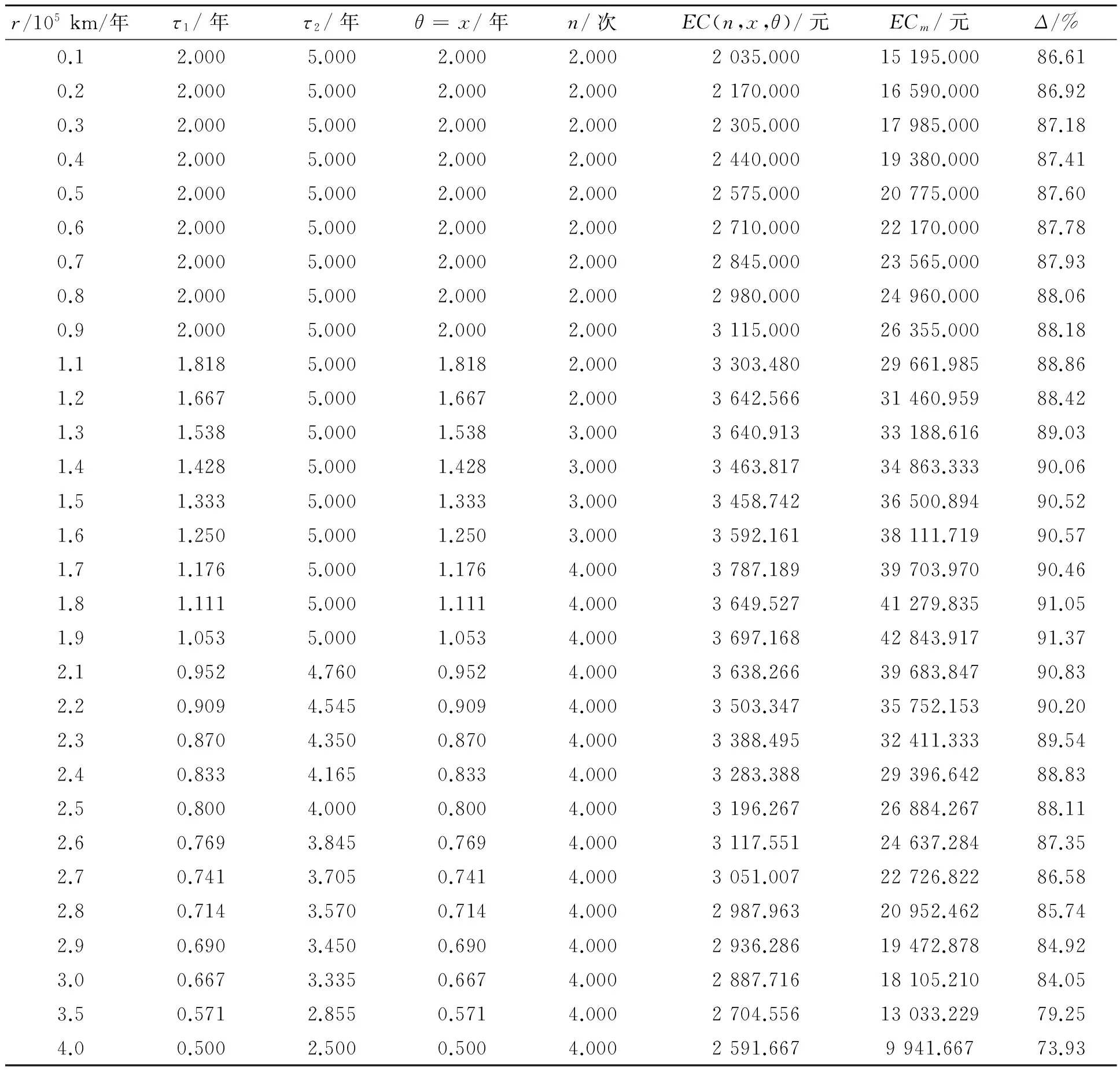
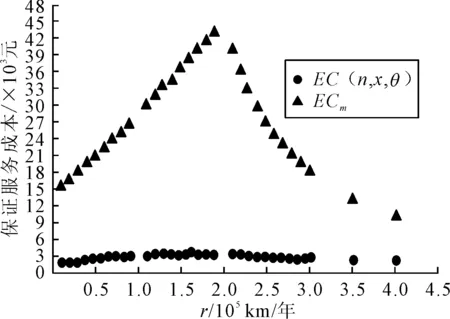
笔者考虑的二维免费维修产品保证范围是由时间及使用程度围成的矩形区域,即基础保证区域为[0,WB]×[0,UB],延伸性保证区域为[WB,WE]×[UB,UE]。由于使用者的使用率不同,那么基础保证及延伸保证区域也不同,二维延伸产品保证区域见表2。假设在基础保证区域内所有的失效都采用最小维修方式进行修复,即经过最小维修后产品的失效率和失效前一刻的失效率相同,产品由失效状态转变为运行状态,则产品的失效过程为非齐次泊松过程。在二维延伸产品保证区域内采用不完全预防性维修方式,即当产品的寿命达到控制限θ(τ1≤θ<τ2)时实施预防性维修,此时T1=θ。Tj(j=1,2,…,n)为实施预防性维修的时间,每次预防性维修之后产品的寿命减少x(0 表2 二维延伸性产品保证策略的保证区域 注:r1=UB/WB,r2=UE/WE 图1 预防性维修对故障率的影响 (2) 笔者根据产品使用者的使用率将二维延伸保证区域分为r1 为了分析和建立延伸产品保证服务成本模型,在R=r的条件下,笔者假设基本产品保证实际结束时间为τ1,延伸产品保证实际结束时间为τ2。在[τ1,τ2]内实施n次预防性维修,令T0=τ1,则Tj(j=1,2,…,n)应该满足τ1=T0≤T1≤T2≤…≤Tn≤τ2。每次预防性维修的成本为Cp,那么延伸保证区域内的预防性维修成本为: ECp=nCp (3) 根据上述模型描述可知,在连续两次预防性维修时间间隔内所有的失效都采用最小维修方式进行修复,每次最小维修的平均成本为Cm。由于每次实施预防性维修,产品的寿命都会减少x个单位时间,那么在[Tj,Tj+1](j=0,1,2,…,n-1)内产品的失效函数为λ(t-jx|r)。因此在该区间内最小维修成本为: Cm[Λ(Tj+1-jx|r)-Λ(Tj-jx|r)]= Cm[Λ(θ|r)-Λ(θ-x|r)] (4) 同理可得,在[Tn,τ2]内的最小维修成本为: Cm[Λ(τ2-nx|r)-Λ(Tn-nx|r)]= Cm[Λ(τ2-nx|r)-Λ(θ-x|r)] (5) 由以上分析可知,在R=r的条件下,延伸性产品保证服务成本为: 也即: ECr(n,x,θ)=nCp+Cm{n[Λ(θ|r)-Λ(θ-x|r)]+Λ(τ2-nx|r)-Λ(τ1|r)} (6) (1)r1 当r x|r)]+Λ(WE-nx|r)-Λ(WB|r)} (7) 同理可得,当r1 (8) (9) 当不考虑R=r条件时,即考虑所有的使用率时,期望延伸性保证服务成本模型为: (10) 图2 r (2)r2 当r 当r2 当r1 当不考虑R=r的条件时,即考虑所有的使用率时,期望延伸性保证服务成本模型为: (12) (3)R=r条件下的保证策略优化。笔者主要是研究考虑预防性维修的二维延伸产品保证策略优化,确定预防性维修的次数n及预防性维修之后产品寿命减少值x,使期望保证服务成本最小化。基于以上分析,在R=r的条件下,对式(6)分别关于θ和x求偏导,可得: nCm[λ(θ|r)-λ(θ-x|r)] (13) nCm[λ(θ-x|r)-λ(τ2-nx)] (14) 笔者所指的产品可以是具有二维免费维修延伸保证产品的一个部件或者模块化单元。产品保证区域为由时间和使用程度围成的矩形区域,时间以年为单位,使用程度为10 000km。设WB=2年,UB=2×10 000 km,WE=5年,UE=10×10 000 km。则可知此时r1=1,r2=2,属于r1 从表3及图3可以看出在不同的使用率条件下,实施了预防性维修服务策略后的二维延伸产品保证服务成本与传统的失效发生后采用最小维修方式进行修复的保证服务成本相比下降显著。在r 表3 不同使用率下的最优预防性维修策略 图3 不同使用率下的保证服务成本 笔者在理论上研究了考虑预防性维修的二维延伸保证策略,即当产品的寿命达到时间控制限时即实施预防性维修,在此基础上建立了二维延伸性产品保证服务成本模型,并将该模型的结果与发生失效时全部采用最小维修方式进行修复相比较,比较的结果显示在不同的产品使用率条件下,当产品的寿命达到预先设置的时间限时实施预防性维修可以显著地降低产品的保证服务成本。该策略可以为制造商或者提供服务的第三方制定延伸保证策略提供参考,同时该服务策略容易实施。但是笔者假定预防性维修的成本是常数,而预防性维修成本在实际应用中应是维修后寿命降低值的函数,未来可以研究预防性维修成本变化对产品保证策略的影响;同时该模型并未考虑延伸产品保证的售价,未来应对制造商或提供产品保证的第三方利润及延伸产品保证的定价进行研究。 [1] CHUN Y H. Optimal number of periodic preventive maintenance operations under warranty[J]. Reliability Engineering & System Safety,1992,37(3):223-225. [2] YEH R H, LO H C. Optimal preventive-maintenance warranty policy for repairable products[J]. European Journal of Operational Research,2001,134(1):59-69. [3] KIM C S, DJAMALUDIN I, MURTHY D N P. Warranty and discrete preventive maintenance[J]. Reliability Engineering & System Safety,2004,84(3):301-309. [4] CHANG W L, LIN J H. Optimal maintenance policy and length of extended warranty within the life cycle of products[J]. Computers & Mathematics with Applications,2012,63(1):144-150. [5] ISKANDAR B P, MURTHY D N P. Repair-replace strategies for two-dimensional warranty policies[J]. Mathematical and Computer Modelling,2003,38(11):1233-1241. [6] ISKANDAR B P, MURTHY D N P, JACK N. A new repair-replace strategy for items sold with a two-dimensional warranty[J]. Computers & Operations Research,2005,32(3):669-682. [7] 于俭,陈相侄.基于最小与缺陷维修的二维产品保证策略研究[J].工业工程与管理,2009,14(3):65-69. [8] BANERJEE R, BHATTACHARJEE M C. Analysis of a two-dimensional warranty servicing strategy with an imperfect repair option[J]. Quality Technology & Quantitative Management,2012,9(1):23-33. [9] JACK N, ISKANDAR B P, MURTHY D N P. A repair-replace strategy based on usage rate for items sold with a two-dimensional warranty[J]. Reliability Engineering & System Safety,2009, 94(2):611-617. [10] 于俭,毛春苗,陈相侄.不完全维修的二维产品保证服务成本[J].工业工程与管理,2010,15(4):57-61. [11] CHUKOVA S, HAYAKAWY, JOHNSTON M. Two dimentional warranty: minimal /complete repair strategy[C]∥Proceedings of the Second Asian International Workshopon Advanced Reliability Modeling (AIWARM 2006). South Korea:[s.n.],2006:361-368. [12] CHUKOVA S, HAYAKAWA Y, JOHNSTON M R. Optimal two-dimensional warranty repair strategy[J]. Journal of Risk and Reliability, 2007,221(4):265-273. [13] SHAHANAGHI K, NOOROSSANA R, JALALI-NAINI S G, et al. Failure modeling and optimizing preventive maintenance strategy during two-dimensional extended warranty contracts[J]. Engineering Failure Analysis,2013(28):90-102. [14] SU C, SHEN J. Analysis of extended warranty policies with different repair options[J]. Engineering Failure Analysis,2012(25):49-62. [15] 仝鹏,刘子先,门峰,等.基于产品使用率的二维延伸性汽车产品保证策略[J].计算机集成制造系统,2014,20(5):1149-1159. JIANG Ran:Postgraduate; School of Management and Economics, Tianjin University, Tianjin 300072, China. [编辑:王志全] Two-dimensional Extended Warranty Strategy Considering Preventive Maintenance JIANGRan,LIUZixian Due to the problem of rising warranty service cost, the preventive maintenance and the corrective maintenance were integrated; and a new two-dimensional warranty strategy considering the preventive maintenance was proposed to solve this problem. A mathematical model of warranty cost was developed to minimize the warranty cost. The optimal warranty strategy was derived to optimize the warranty cost based on the different usage rates. Finally, numerical analysis was compared with the cost of minimal repair strategy. The results indicate that the warranty cost is reduced significantly. warranty; preventive maintenance; warranty service cost model; warranty strategy 2015-07-12. 蒋冉(1989-),女,山东枣庄人,天津大学管理与经济学部硕士研究生. 国家自然科学基金资助项目(71171142);高等学校博士学科点专项科研基金资助项目(20110032110034). 2095-3852(2015)06-0816-06 A F224 10.3963/j.issn.2095-3852.2015.06.034
2 延伸产品保证服务成本模型
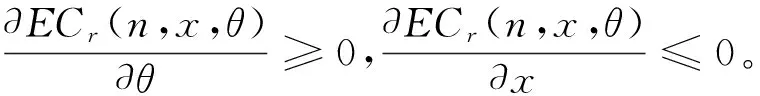
3 数值分析
4 结论
