一种改正伪距多路径误差的北斗三频周跳探测与修复方法

肖国锐 隋立芬 戚国宾 刘乾坤

1 信息工程大学地理空间信息学院，郑州市科学大道62号，450001

周跳探测与修复和模糊度解算是GNSS 测量数据处理的关键问题［1－2］。随着GPS的现代化以及欧洲Galileo 和我国BDS 的建成，未来GNSS导航定位将能获得三频观测数据［3］。多位学者对GNSS 三频数据周跳探测与修复进行研究［4－18］。文献［2］推导了GNSS三频伪距相位组合探测周跳的阈值条件，以组合周跳估值标准差最小为原则选取不同伪距噪声条件下的GPS三频最优伪距相位组合，可实时探测与修复所有周跳；文献［12］根据多频数据组合原理，分析了BDS伪距和相位的多种可能组合，并选取3种线性无关的优化组合估计与修复周跳；文献［11］采用三频无几何相位组合探测周跳，通过2个无几何相位和一个三频伪距相位组合联合修复周跳，并采用搜索法克服方程解的不稳定问题；文献［4］同样利用三频无几何相位组合探测周跳，通过类似LAMBDA 算法搜索周跳候选组来确定周跳。

GNSS三频周跳的探测与修复主要有2种思路：通过选取3个线性无关的伪距相位组合来探测并修复周跳；通过选取2个线性无关的无几何相位组合来探测周跳，增加一个伪距相位组合来修复周跳。无论采用哪种算法，周跳修复过程中伪距信号的质量至关重要，直接影响周跳修复的效果。

多位学者对导航卫星系统测距信号质量进行了分 析［19－21］，利用三频观测值导出MP组合来考察测站伪距多路径误差。本文借鉴其思路，利用北斗实测三频数据分析伪距多路径误差对北斗三频周跳探测与修复的影响，提出一种改正伪距多路径误差的北斗三频周跳探测与修复方法。

1 伪距多路径改正的北斗三频周跳探测与修复方法

1.1 周跳探测

三频伪距、相位组合观测量方程可表示为［8］：

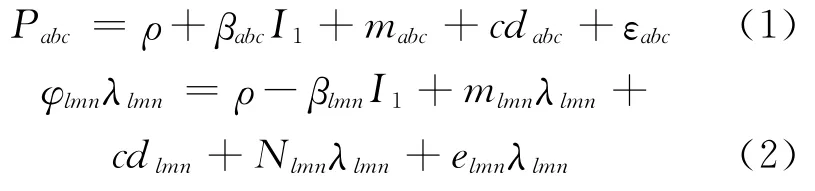
式中，ρ为卫星至接收机的几何距离（包括卫星钟差、接收机钟差、对流层误差等）；βabc、βlmn分别为伪距组合观测量和相位组合观测量的电离层延迟影响系数，a、b、c∈R，a＋b＋c＝1，l、m、n∈Z；I1为载频f1上的电离层延迟；mabc、mlmn分别为伪距组合观测量和相位组合观测量的多路径误差；dabc、dlmn分别为伪距组合观测量和相位组合观测量的硬件延迟；Nlmn和λlmn分别为相位组合观测量的模糊度和波长；εabc和elmn分别为伪距组合观测量和相位组合观测量的观测噪声；R和Z分别代表实数集和整数集。

伪距相位组合周跳检验量的定义为：由式（1）减去式（2），并在相邻历元之间求差［8］：

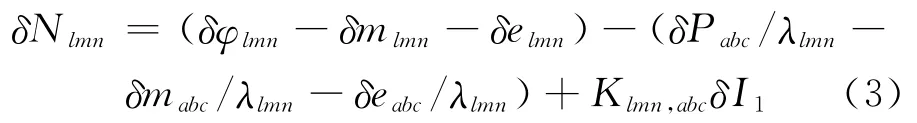
无几何相位组合周跳检验量的定义为：令式（2）中l＋m＋n＝0，并在相邻历元之间求差［11］：

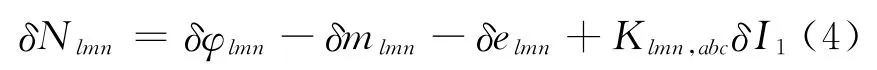
两种周跳检验量中，由于硬件时延随时间变化缓慢，因此在相邻历元求差时可消除硬件时延项。假设历元间载频f1上电离层延迟变化δI1很小，如果系数Klmn，abc较小，则历元间电离层延迟变化项也可忽略，或者视为噪声［2，12］。

在北斗系统中，由于接收机伪距多路径误差较大且变化快，并不能通过历元间差分完全消除，残留的伪距多路径误差将严重影响伪距载波周跳探测及修复。而北斗无几何相位组合仅受载波噪声影响，且其电离层延迟较小，虽然每个无几何相位均存在无法探测的不敏感周跳，但通过筛选2个无几何相位组合进行联合探测可以较好地解决不敏感周跳的问题［11］，故本文选择无几何相位组合探测周跳。

1.2 周跳确定及验证

结合式（3）和式（4）可构建如下模型修复周跳［2，11］：

借鉴已有研究［14，18］，本文选取由式（3）构建的3组线性无关的伪距相位组合（－1，－5，6）、（1，4，－5）、（－4，1，4）来确定周跳。

文献［11］利用式（3）和式（2）构建的2个线性无关的无几何相位组合和1个伪距相位组合来确定周跳，本文选取无几何相位组合（1，1，－2）、（1，－2，1）和伪距相位组合（1，3，－4）来确定周跳。

引入周跳验证步骤，以检验其是否正确。将修复后的相位观测量代入式（4）重新计算，如果此时无几何相位组合周跳检验量小于阈值，说明周跳修复正确。如果此时无几何相位组合周跳检验量仍然大于阈值，则进行下一步伪距多路径效应改正，并重新确定周跳。

1.3 伪距多路径误差改正

为了推导方便，北斗单频伪距和相位方程可表示为［21］：

式中，P和φ分别为伪距和相位观测值；ρ为与频率无关项；BP为硬件延迟；I为电离层斜延迟；mP、mφ分别为伪距和相位多路径误差；A为含初始相位偏差的模糊度参数；λ为波长因子；εP、εφ分别为两类观测值的观测噪声，且满足（ε）＝0。

利用北斗三频观测值可单独考察对应于频段i的伪距多路径误差。MP组合具体形式为：

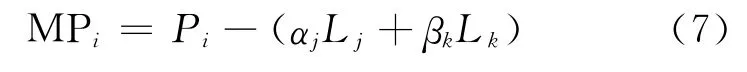
其中，i、j、k为北斗三频相位观测值的频段，

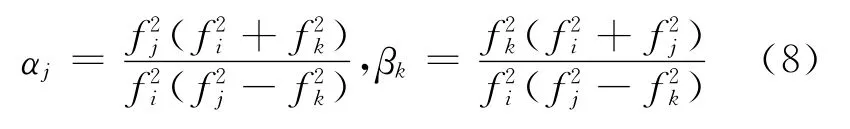
显然，αj＋βk＝1。此组合消去了几何距离和电离层延迟的影响［16］。将式（6）和式（8）代入式（7），可得：

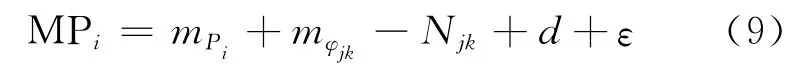
其中，

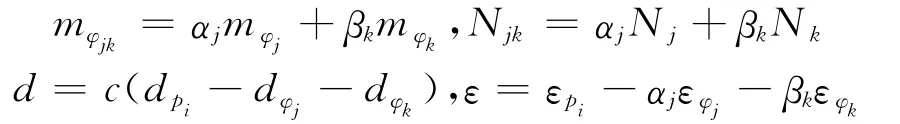
假设多路径具有周期性，在n个历元里可以取平均值，则式（9）中的常数项可以表示为：

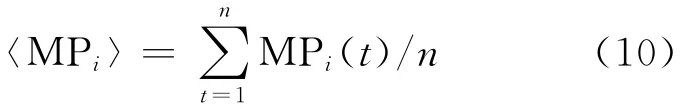
可得到频段i的伪距多路径误差：

最后，可求得改正后的伪距观测值为：

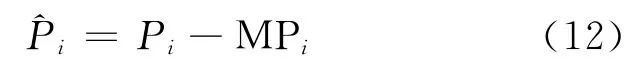
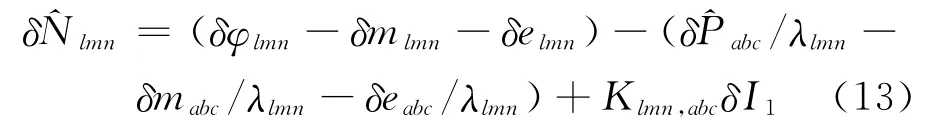
图1 算法流程图Fig.1 Flow diagram of algorithm

2 算例分析与比较

实验分析了某测站的北斗静态观测数据，观测时间为2012－10－07，采样间隔为1s，可接收3个频点的相位及伪距观测量。为了分析不同采样间隔的影响，直接对原始数据进行重新采样，以获得10s、30s采样间隔的观测数据。经相关方法检测，原始数据没有周跳。

2.1 测站伪距多路径效应分析

图2是由式（11）提取的1号卫星B1频点伪距多路径误差。从图2看出，北斗卫星伪距多路径误差存在明显的周期性，其误差在部分历元达2m。

图2 1号卫星B1 频点多路径误差图Fig.2 Multipath errors of B1from PRN1satellite

由式（3）可知，伪距多路径误差历元间差分残留误差将直接影响周跳的探测与修复精度。图3给出了伪距多路径误差历元间差分后残留的误差。

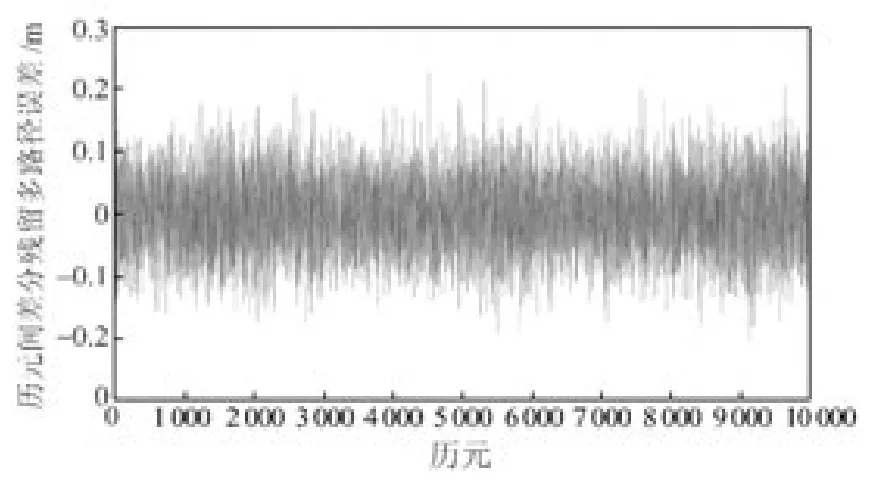
图3 1号卫星B1 频点多路径误差历元间差分残留的误差Fig.3 Epoch differenced multipath errors of B1from PRN1satellite

由图3看出，伪距多路径误差历元间差分后残留误差仍然达到0.1m，部分历元超过0.2m，B1频点载波相位的周长是0.192m，残留的多路径误差仍然较大，需要进行改正。在采样率较低的情况下，伪距多路径误差历元间差分残留误差更大，会产生更大影响。

图4 伪距相位组合周跳检验量Fig.4 Cycle－slip detection using code－phase combinations

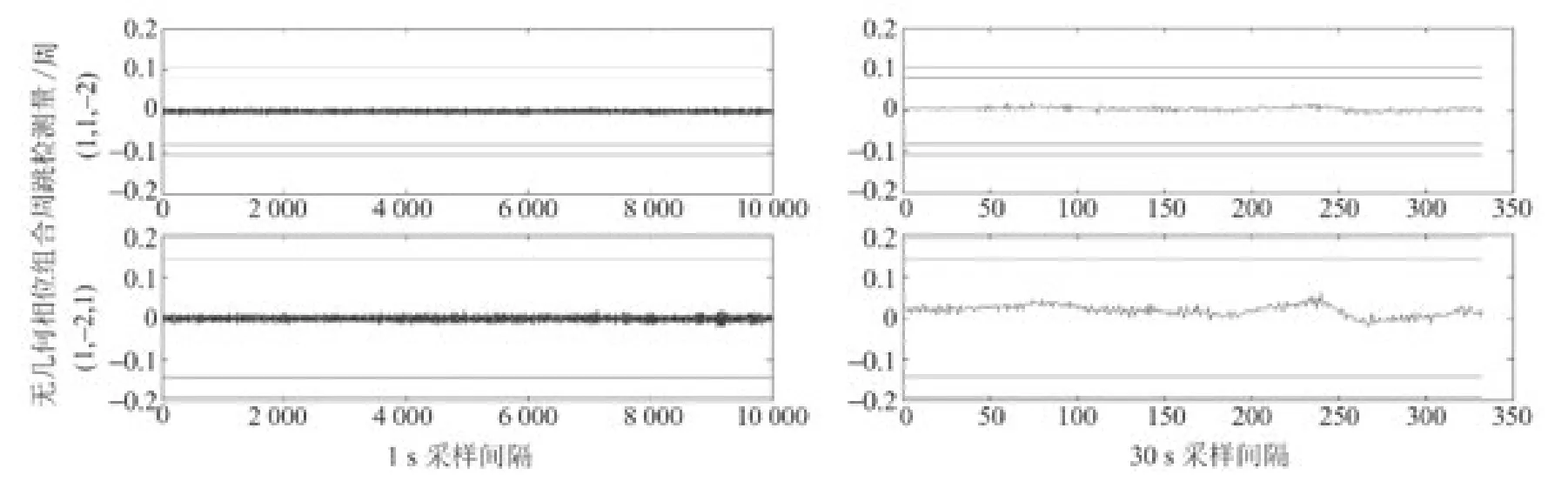
图5 无几何相位组合周跳检验量Fig.5 Cycle－slip detection using geometry－free phase combinations

2.2 周跳检验量分析

图4 为伪距相位组合（－1，－5，6）、（1，4，－5）、（－4，1，4）的周跳检验量，图5为无几何相位组合（1，1，－2）、（1，－2，1）的周跳检验量，图中周跳检验量上下两条线对应于3、4倍中误差的周跳探测阈值。

由图4、5可以得出如下结论：

1）对比不同采样间隔下两种组合周跳检验量可知，无几何相位周跳检验量明显小于伪距相位组合检验量，其精度更高。当采样间隔为1s时，无几何相位周跳检验量在0.005周以内，而伪距相位组合周跳检验量在0.1周以内。

2）当采样间隔增大时，伪距相位组合周跳检验量逐步增大，接近3倍中误差的阈值并呈现一定的周期性，原因可能是受历元间差分残留误差的影响。当采样率达到30s时，可以看到（－4，1，4）组合在部分历元已经超出4倍中误差，会产生误判。

从上节可知，北斗接收机伪距多路径误差影响较大且变化快，在较大采样间隔下不能通过历元间差分完全消除。而北斗无几何相位组合仅受载波噪声影响，其周跳检验量精度更高。故本文选择使用2个无几何相位组合（1，1，－2）、（1，－2，1）进行周跳探测。

2.3 伪距多路径误差改正后周跳确认

为了分析周跳修复效果，每5个历元在每个频点上加入1～1 000周的随机周跳，使用无几何相位组合和伪距相位组合进行周跳确定。分别用2种方案：方案一，使用原始伪距观测值进行周跳确定；方案二，使用经过多路径误差改正后的伪距观测值。两种方案效果如表1所示。

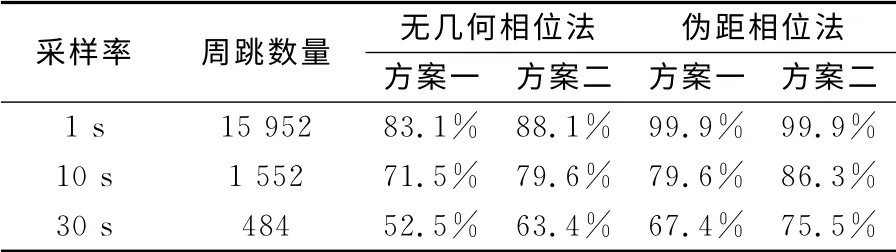
表1 2种方案周跳确定成功率对比Tab.1 Success rate of two schemes

从表1可以得出如下结论：

1）伪距相位法及无几何相位法确定周跳的成功率随着采样间隔的增大急剧下降，主要是因为采样间隔较大时，历元间差分不能很好地消去电离层、多路径等误差。伪距相位法成功率较无几何相位法要高，原因可能是利用公式X＝（ATA）－1ATL确定周跳时，（ATA）－1条件数很大，从而导致L取值的稍微变动会使解产生较大的变化［11］，更容易受到伪距多路径误差的影响。

2）无论采用哪种周跳确定方法，方案二的周跳确定成功率都要高于方案一，尤其在采样间隔较大时更为明显，这说明伪距多路径误差对周跳确定产生了一定的影响，对伪距多路径误差进行改正能抑制其影响。当采样间隔较大时，两种方法都不能正确确定所有周跳，可能是因为电离层误差产生了影响，需要进一步研究。

3 结 语

本文利用北斗三频观测值提取伪距多路径误差并进行分析，结果表明伪距多路径误差存在周期性且变化较快，历元间差分处理不能完全消除其影响，必须对其进行改正。本文方法提高了周跳确定的成功率，一定程度上抑制了伪距多路径误差的影响，有一定的应用价值。值得注意的是，本文所使用的伪距多路径误差提取方法仍受限于原始数据的质量，如何对多路径误差进行建模分析值得进一步研究。

［1］李征航，黄劲松.GPS 测量与数据处理［M］.武汉：武汉大学出版社，2005（Li Zhenghang，Huang Jinsong.GPS Surveying and Data Processing［M］.Wuhan：Wuhan University Press，2005）

［2］李金龙，杨元喜，徐君毅，等.基于伪距相位组合实时探测与修复GNSS 三频非差观测数据周跳［J］.测绘学报，2011，40（6）：717－722（Li Jinlong，Yang Yuanxi，Xu Junyi，et al.Real－Time Cycle－Slip Detection and Repair Based on Code－Phase Combinations for GNSS Triple－Frequency Un－Differenced Observations［J］.Acta Geodaetica et Cartographica Sinica，2011，40（6）：717－722）

［3］杨元喜.北斗卫星导航系统的进展、贡献与挑战［J］.测绘学报，2010，39（1）：1－6（Yang Yuanxi.Process，Contribution and Challenges of Compass／Beidou Satellite Navigation System［J］.Acta Geodaetica et Cartographica Sinica，2010，39（1）：1－6）

［4］Dai Z，Knedlik S，Loffeld O.Real－Time Cycle－Slip Detection and Determination for Multiple Frequency GNSS［C］.Positioning，Navigation and Communication，2008

［5］Lacy M C，Reguzzoni M，SansòF.Real－Time Cycle Slip Detection in Triple－Frequency GNSS［J］.GPS Solutions，2012，16（3）：353－362

［6］Dai Z，Knedlik S，Loffeld O.Instantaneous Triple－Frequency GPS Cycle－Slip Detection and Repair［J］.International Journal of Navigation and Observation，2009（1）：1－14

［7］范建军，王飞雪，郭桂蓉.GPS 三频非差观测数据周跳的自动探测与改正研究［J］.测绘科学，2006，31（5）：24－26（Fan Jianjun，Wang Feixue，Guo Guirong.Automated Cycle Slip Detection and Repairation of GPS Triple－Frequency Undifference Data［J］.Science of Surveying and Mapping，2006，31（5）：24－26）

［8］李金龙.GNSS 三频精密定位数据处理方法研究［D］.郑州：信息工程大学，2011（Li Jinlong.Researches on the Algorithms of GNSS Triple Frequency Precise Positioning［D］.Zhengzhou：Information Engineering University，2011）

［9］Liu Z.A New Automated Cycle Slip Detection and Repair Method for a Single Dual－Frequency GPS Receiver［J］.Journal of Geodesy，2011，85（3）：171－183

［10］刘旭春，伍岳，张正禄，等.GPS 三频数据在周跳和粗差探测与修复中的应用［J］.煤炭学报，2006，31（5）：585－588（Liu Xuchun，Wu Yue，Zhang Zhenglu，et al.Application of GPS Triple－Frequency Data in Detection and Repair of Cycle Slip and Gross Error［J］.Journal of China Coal Society，2006，31（5）：585－588）

［11］黄令勇，宋力杰，王琰，等.北斗三频无几何相位组合周跳探测与修复［J］.测绘学报，2012，41（5）：763－768（Huang Lingyong，Song Lijie，Wang Yan，et al.Beidou Triple－Frequency Geometry－Free Phase Combination for Cycle－Slip Detection and Correction［J］.Acta Geodaetica et Cartographica Sinica，2012，41（5）：763－768）

［12］孙保琪，欧吉坤，盛传贞，等.一种适于Compass周跳探测的三频数据优化组合［J］.武汉大学学报：信息科学版，2010，35（10）：1 157－1 160（Sun Baoqi，Ou Jikun，Sheng Chuanzhen，et al.Optimal Multi－Frequency Data Combination for Compass Cycle Slip Detection and Repairation［J］.Geomatics and Information Science of Wuhan University，2010，35（10）：1 157－1 160）

［13］熊伟，伍岳，孙振冰，等.多频数据组合在周跳探测和修复上的应用［J］.武汉大学学报：信息科学版，2007，32（4）：319－322（Xiong Wei，Wu Yue，Sun Zhengbing，et al.Application of Multi－Frequency Combination Observation in Cycle Slip Detection and Restoration［J］.Geomatics and Information Science of Wuhan University，2007，32（4）：319－322）

［14］罗腾，白征东，过静珺.两种周跳探测方法在北斗三频中的应用比较研究［J］.测绘通报，2011，4（1）：1－3（Luo Teng，Bai Zhengdong，Guo Jingjun.Comparative Study of Two Kinds of Cycle Slip Detection Methods in the Application of Beidou Tri－Frequency［J］.Bulletin of Surverying and Mapping，2011，4（1）：1－3）

［15］伍岳.第二代导航卫星系统多频数据处理理论及应用［D］.武汉：武汉大学，2005（Wu Yue.The Theory and Application on Multi－Frequency Data Processing of GNSS 2［D］.Wuhan：Wuhan University，2005）

［16］刘旭春，伍岳，黄学斌，等.多频组合数据在原始载波观测值预处理中的应用［J］.测绘通报，2007（2）：14－18（Liu Xuchun，Wu Yue，Huang Xuebin，et al.Application of GPS Multi－Frquency Carrier Phase Combinations for Preprocessing of Original Carrier Phase Observations［J］.Bulletin of Surverying and Mapping，2007（2）：14－18）

［17］王拓，吕志伟，王贺.三频数据组合进行周跳和粗差探测方法研究［J］.测绘科学与工程，2012，32（1）：28－33（Wang Tuo，Lv Zhiwei，Wang He.Study of Detecting Capability for Cycle Slip And Gross Error Using Triple－Frequency Data［J］.Geomatic Science and Engineering，2012，32（1）：28－33）

［18］周巍，郝金明，冯淑萍.北斗三频数据周跳的探测方法［J］.测绘科学技术学报，2012，29（2）：87－90（Zhou Wei，Hao Jinming，Feng Shuping.A Method of Cycle－Slip Detection on Triple－Frequency Data of Beidou［J］.Journal of Geomatics Science and Technology，2012，29（2）：87－90）

［19］Bakker P F，Tiberius C C J M，Marel H，et al.Short and Zero Baseline Analysis of GPS L1C／A，L5Q，GIOVE E1B，and E5aQ Signals［J］.GPS Solutions，2012，16（1）：53－64

［20］Hauschild A，Montenbruck O，Sleewaegen J M，et al.Characterization of Compass M－1Signals［J］.GPS Solutions，2012，16（1）：117－126

［21］程鹏飞，李玮，秘金钟.北斗导航卫星系统测距信号的精度分析［J］.测绘学报，2012，41（5）：690－695（Cheng Pengfei，Li Wei，Bei Jinzhong.Precision Analysis of Beidou Range Measurement Signals［J］.Acta Geodaetica et Cartographica Sinica，2012，41（5）：690－695）