利用EMD阈值消噪改进MW 组合周跳探测性能

甘 雨 隋立芬 戚国宾 温劲杰

1 信息工程大学地理空间信息学院，郑州市科学大道62号，450001

2 93787部队，北京市，100076

GPS 动态非差周跳探测一般需使用多频观测值，如无几何距离组合［1，2］、MW组合［3］等。Blewitt提出的TurboEdit算法［4］使用这两种组合观测值联合探测周跳，目前已得到广泛应用［5］。TurboEdit算法中，MW 组合通过递推平均来估计均值和方差，由于估值需逐渐收敛，收敛前出现的周跳无法探测［6］。此外，MW 组合包含伪距观测值，其噪声远大于载波相位，受多路径效应和卫星高度角等因素的影响，可能无法探测1～2周的小周跳［7］。因为递推平均过程虽然能减小期望和方差估值受噪声的影响，但是MW 观测值本身的噪声水平并没有降低。蔡昌盛［7］对本历元使用后向平滑，在其后一个历元使用前向平滑，以前后历元差作为探测检验量以减少噪声影响，但是要求后续历元用于平滑的数据一定不含周跳，降低了实际应用中的效率和自动化程度。部分学者将小波分析等用于周跳探测，但均针对原始GPS观测值［8－9］。在动态导航定位中，接收机的某些运动可能引起原始观测值发生类似于周跳的突变。

针对MW 组合噪声水平较高的情况，使用经验模分解（empirical mode decomposition，EMD）阈值消噪的方法进行处理。对于EMD 的端点效应问题，提出在MW 递推均值上增加虚拟噪声构成虚拟观测值的方法对数据进行延拓。对MW组合进行分解，估计各层分量的阈值，削弱噪声影响。分析消噪前后含周跳MW 组合所发生的变化，指出周跳具有“扩散”现象，提出基于消噪后MW 组合的探测方案。

1 MW 组合探测性能分析

MW 组合观测值为［4］：

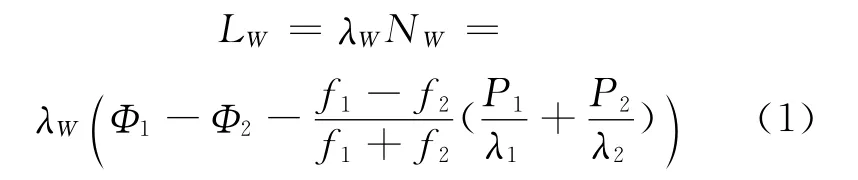
其中，Φ表示载波相位观测值，P表示伪距，f表示频率，λ表示波长。该组合消除了几何距离和大部分误差项，仅受伪距噪声和多路径效应影响。

宽巷波长λW表达式为：

c为光速，波长约为86.2cm，相比原始L1和L2增加数倍。直接以下式进行分析：

若无特别说明，这里MW 组合观测均指NW。

假设两个频点的伪距精度相同（均为σP），载波相位误差很小（可忽略），则MW 组合的精度为：

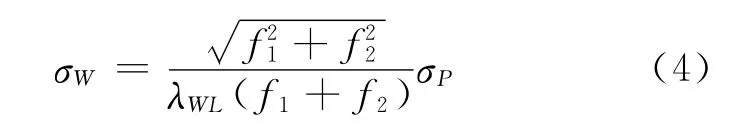
单位为周。代入具体频率和宽巷波长，得：

若以4倍中误差作为周跳探测的阈值，要探测1周的周跳，需要

才能满足σW＜1／4＝0.25的需求。受到高度角和多路径效应影响，式（6）的条件有时难以满足，在动态条件下尤为严重。

MW 组合递推平均计算均值和方差为［4］：

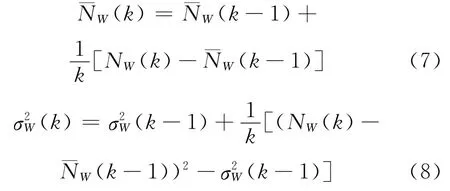
σW初值取为0.5周。若

则认为k历元发生周跳。

可以看出，在周跳探测过程中，NW本身受到噪声和多路径效应的影响。若误差水平较高，有可能发生漏检。

图1显示的是某动态测站在一段时间内观测卫星PRN10（高度角大于55°）无周跳时的MW组合观测值（这里实际上是，去除了均值）及其阈值。可以看出，MW 组合的噪声水平较高，分布在［－0.664，0.598］范围内。显然，在某些历元内发生1周的小周跳时无法被探测。图2 中，黑色虚线以下的部分若发生＋1周的周跳，无法探测出来；而图3中，黑色虚线以上的部分无法探测可能发生的－1周的周跳。

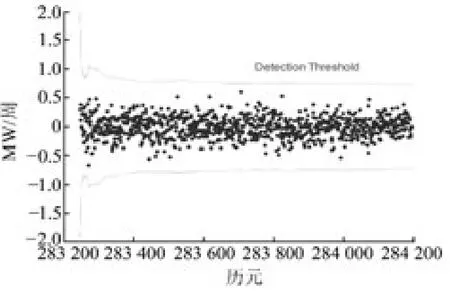
图1 无周跳时MW 组合及阈值Fig.1 MW and thresholds（0cycle slip）

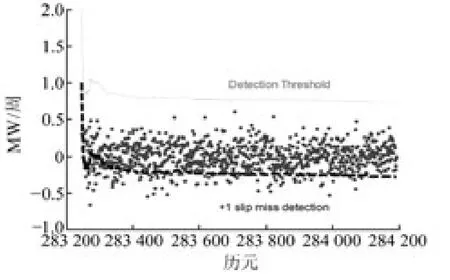
图2 ＋1周周跳时的漏检区域Fig.2 Miss detection area（＋1cycle slip）

图3 －1周周跳时的漏检区域Fig.3 Miss detection area（－1cycle slip）

如果能够降低MW 组合观测值的噪声水平，同时合理地估计降噪后观测的均值和方差，就能探测出小周跳，减小漏检率。

2 EMD 阈值消噪MW 组合的周跳探测

2.1 EMD原理及端点效应的抑制

经验模分解［10］能把复杂的信号分解为一系列固有模态函数（IMF，intrinsic mode function）分量和余项之和的形式。分解出的各分量频率由高到低，每个分量为一零均值平稳信号。分解的具体过程为：

1）根据信号x（t）的局部极大值和极小值，用三次样条曲线插值求出信号上下包络线，计算上下包络的均值m1，得到h1＝x（t）－m1。检测h1是否满足IMF的两个条件：①零点数目与极值点数目相同或最多相差1；②局部极大值点构成的包络线和局部极小值点构成的包络线的均值为零。若满足，则h1为第一个分量imf1。

2）若不满足，重复执行第1步，直至重复k次后h1k满足条件，则imf1＝h1k，求出原始信号与imf1的差值：r1＝x（t）－imf1。

3）将r1作为新原始信号重复上述过程，逐个提取出n个IMF分量imf2，imf3，…，imfn，得到余项rn＝rn－1－imfn。当imfn或rn小于预先设定的值，或rn已经成为单调函数时，分解完成。信号x（t）分解成n个IMF分量和1个余项的和：

在分解过程中，求包络线是通过极值点进行插值拟合得到的，在样条插值时，如果数据两个端点本身不是极值点，就不能确定端点处的极值点，导致构成包络线的三次样条曲线在数据序列的两端出现发散现象，并且这种发散的结果可能会逐渐向内“污染”，这就是EMD 端点效应［11］。

如果在MW 组合消噪过程中发生周跳，且周跳位置发生在数据段的边缘，端点效应会对含周跳的组合观测值进行错误的分解，导致周跳被湮没。如果能对数据进行延拓，即在端点以外再增加一段虚拟观测数据，则原来发生周跳的数据处于数据中部，受端点效应的影响将大大降低，关键在于所增加的数据要和已有数据具有类似的特性。

在第k个历元，我们由之前k－1个历元的数据经递推平均能够得到数据的均值和标准差σW（k－1），在假定MW 组合观测符合正态分布的情况下，可以产生n个虚拟数据：

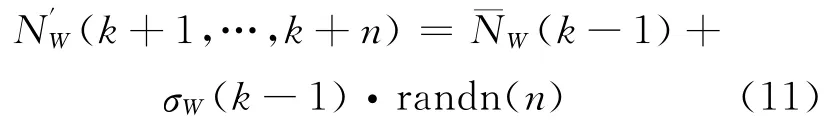
其中，randn产生标准正态分布的随机数组。此为向后延拓的方向，向前延拓方法类似。

2.2 EMD 阈值消噪

文献［13－14］提出了基于Hurst参数的阈值消噪方法。对前两个IMF分量的标准差采用具有抗差性的中位数来估计，以免受到周跳成分的干扰：

而其他IMF分量的方差按下式递推计算：

式中，H即为Hurst参数。MW 组合观测值误差可视为白噪声，即H＝0.5，则：

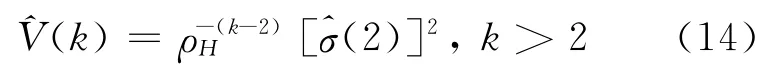
阈值估计：

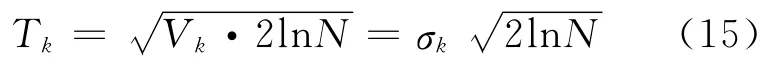
可以看出，各层分量的阈值不同，EMD 阈值消噪是一种自适应阈值消噪方法。

MW 组合观测值如图4 所示。对卫星PRN10的一段数据最后一个历元的MW 组合加入＋1周周跳，分别用原始数据和数据延拓后的数据进行EMD 阈值消噪，结果见图5、6。可以看出，如果不对数据进行延拓，受端点效应的影响，周跳会被湮没。

图4 端点发生周跳的MW 组合Fig.4 MW with cycle slip on the end

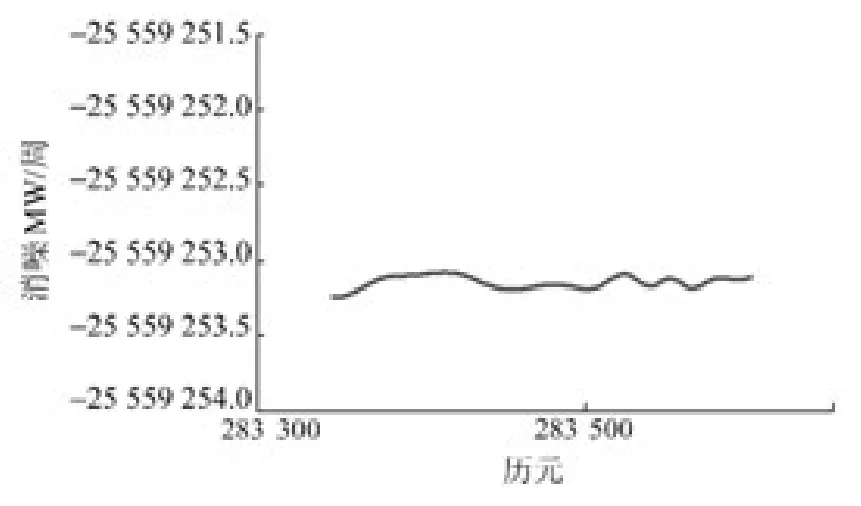
图5 未使用数据延拓的消噪MWFig.5 De－noised MW without data extension

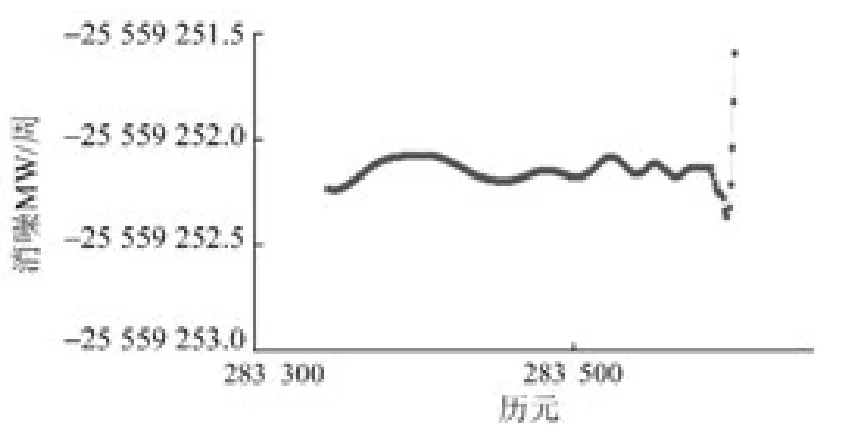
图6 使用数据延拓的消噪MWFig.6 De－noised MW with data extension

2.3 消噪MW 组合探测周跳

MW 组合中的观测值若发生周跳，相当于数据发生极强的突变，EMD 阈值消噪将这种突变进行平滑，让整个数据的变化更为平缓。因此，某个历元上发生的周跳经过阈值消噪后，会“扩散”到附近的历元，如图6。图7、8是另一段MW 组合观测值及其消噪的结果，周跳未发生在端点处而是发生在中间，周跳向前后两个方向扩散。

消噪后周跳的“扩散”现象对于周跳的发现是有利的。假设在k历元发生周跳，则对k－1历元及之前历元的数据，采用EMD 阈值消噪后MW组合未发生突变，即k－1、k－2…等历元均无法探测到周跳；而使用包含k历元的数据进行消噪后，组合观测值在k、k－1、k－2…等历元均可能超过检验阈值。这说明，使用消噪后的MW 组合探测周跳时，不能仅以是否超过检验阈值作为定位周跳发生历元的标准，需结合前后两个历元的结果进行对比。

消噪MW 组合进行周跳探测包括以下步骤：

1）基于递推平均过程估计的均值和方差，对MW 组合观测值序列进行数据延拓，如式（11）所示。对于消噪后的数据，可取标准差初值为0.2周或更小。

2）对信号进行EMD 分解，并进行阈值消噪。

3）对于消噪后MW 组合超过阈值的点i、i＋1、i＋2、…，由k＝i及之前一段历元的数据进行步骤1、2，检验消噪后k历元结果是否超过阈值。若超出，则说明k历元发生周跳，将k历元结果用递推平均计算的均值代替，以免影响后续探测，k往前推进，即k＝i＋1；若未超出，说明当前历元未发生周跳，直接令k＝i＋1。最终使k遍历所有超过阈值的点。上述步骤也可由后向前递推。

图7 发生周跳的MW 组合Fig.7 Un－de－noised MW with cycle slip

图8 消噪后发生周跳的MW 组合Fig.8 De－noised MW with cycle slip

3 计算与分析

选择256个历元数据进行实验，未消噪MW组合的误差与图1类似。其中，第256个历元的MW 组合观测值加入＋1 周的周跳，进行EMD阈值消噪前均进行了数据延拓。图9显示的是使用前255个历元数据探测的结果，图10为256个历元数据探测的结果。使用少于255个历元的结果和图9类似，这里不再给出。

由上述结果可以看出：

1）经过消噪后，MW 组合观测值的噪声水平下降，最大值不超过0.2周，能够迅速探测出小至1周的周跳。

2）对数据进行数据延拓后再使用EMD，能探测到位于端点处的周跳。

3）发生周跳时，若使用包含周跳对应历元的数据进行消噪并探测，其他历元也受到周跳的影响，结合使用不含周跳历元的数据方能最终确定周跳位置。

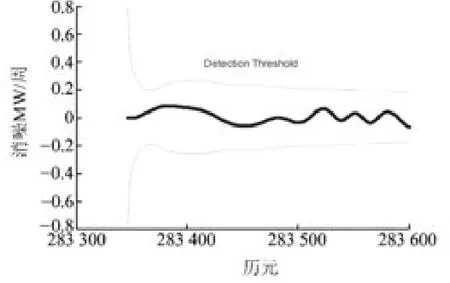
图9 发生周跳的MW 组合Fig.9 Un－de－noised MW with cycle slip

图10 消噪后发生周跳的MW 组合Fig.10 De－noised MW with cycle slip

4 结 语

TurboEdit方法无法降低MW 组合观测值本身的噪声水平，在接收机质量不稳定、多路径效应显著等情况下容易造成漏检。使用EMD 阈值消噪的方法能够对噪声进行降噪处理，根据噪声特性得到各层分量的阈值，削弱噪声影响，提高对周跳的辨识度。EMD 存在端点效应问题，提出在MW 递推均值上增加虚拟噪声构成虚拟观测值的方法对数据进行延拓。进行数据延拓后，即使在端点处发生周跳，消噪后周跳特性仍然得到保留。若MW 组合包含周跳，则消噪后观测值中的周跳具有“扩散”现象。针对这一现象提出的基于消噪后MW 组合的探测方案，能够定位周跳发生的具体位置，增强消噪后MW 组合探测周跳的准确性。

［1］方荣新，施闯，魏娜，等.GPS数据质量控制中实时周跳探测研究［J］.武汉大学学报：信息科学版，34（9）：1 094－1 098（Fang Rongxin，Shi Chuang，Wei Na，et al.Realtime Cycle－Slip Detection for Quality Control of GPS Measurements［J］.Geomatics and Information Science of Wuhan University，34（9）：1 094－1 098）

［2］陈品馨，章传银，黄昆学.用相位减伪距法和电离层残差法探测和修复周跳［J］.大地测量与地球动力学，2010，30（2）：120－125（Chen Pinxin，Zhang Chuanyin，Huang Kunxue.Cycle Slips Detecting and Repairing by Use of Phase Reduce Pseudorange Law and Ionized Layer Remant Method of Difference［J］.Journal of Geodesy and Geodynamics，2010，30（2）：120－125）

［3］阳仁贵，欧吉坤，袁运斌.一种GPS相位周跳分段平均组合的自动修复方法［J］.大地测量与地球动力学，2009，29（5）：76－77（Yang Rengui，Ou Jikun，Yuan Yunbin.An Approach of Sub－Average Joint Computation for Auto Restoring GPS Phase Cycle Slip［J］.Journal of Geodesy and Geodynamics，2009，29（5）：76－77）

［4］Blewitt G.An Automatic Editing Algorithm for GPS Data［J］.Geophysical Research Letters，1990，17（3）：199－202

［5］吴继忠，施闯，方荣新.TurboEdit单站GPS数据周跳探测方法的改进［J］.武汉大学学报：信息科学版，2011，36（1）：29－34（Wu Jizhong，Shi Chuang，Fang Rongxin.Improving the Single Station Data Cycle Slip Detection Approach TurboEdit［J］.Geomatics and Information Science of Wuhan University，2011，36（1）：29－34）

［6］郑作亚，程宗颐，黄城，等.对Blewitt周跳探测与修复方法的改进［J］.天文学报，2005，46（2）：216－225（Zheng Zuoya，Cheng Zongyi，Huang Cheng，et al.Improving of Cycleslip Detection and Correction of Blewitt Method［J］.Acta Astronomica Sinica，2005，46（2）：216－225）

［7］Cai Changsheng，Liu Zhizhao，Xia Pengfei，et al.Cycle Slip Detection and Repair for Undifferenced GPS Observations under High Ionospheric Activity［J］.GPS Solution，2013，17：247－260

［8］蔡昌盛，高井祥.GPS周跳探测及修复的小波变换法［J］.武汉大学学报：信息科学版，2007，32（1）：39－43（Cai Changsheng，Gao Jingxiang.Cycle－slip Detection and Correction of GPS Data by Wavelet Transform［J］.Geomatics and Information Science of Wuhan University，2007，32（1）：39－43）

［9］李明然，田林亚，热比亚.小波和Kalman滤波组合在GPS周跳探测与修复中的应用［J］.大地测量与地球动力学，2012，32（4）：76－79（Li Mingran，Tian Linya，Rebiya.Application of Wavelet and Kalman Filtering Combination in GPS Cycle Slip Detection and Restoration［J］.Journal of Geodesy and Geodynamics，2012，32（4）：76－79）

［10］Huang N E，Shen Z，Long S R，et al.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Nonstationary Time Series Analysis［J］.Proceedings of the Royal Society：A，1998，1971，454：903－993

［11］曹冲锋，杨世锡，杨将新.一种抑制EMD 端点效应新方法及其在信号特征提取中的应用［J］.振动工程学报，2008，21（6）：588－594（Cao Chongfeng，Yang Shixi，Yang Jiangxin.A New Method for Restraining the End Effect of Empirical Mode Decomposition and its Applications to Signal Feature Extraction［J］.Journal of Vibration Engineering，2008，21（6）：588－594）

［12］Huang N E，Shen S S P.Hilbert－Huang Transform and Its Applications［M］.Singapore：World Scientific，2005

［13］甘雨，隋立芬，王冰.经验模态分解阈值消噪方法及其在惯性导航系统数据处理中的应用［J］.测绘学报，2012，41（4）：504－510（Gan Yu，Sui Lifen，Wang Bing.EMD Threshold De－Noising and Its Applications in INS Data Processing［J］.Acta Geodaetica et Cartographica Sinica，2012，41（4）：504－510）

［14］Gan Yu，Sui Lifen.An EMDThreshold De－Noising Method for Inertial Sensors［J］.Measurement，2014，49：34－41