基于失业率与通货膨胀率的我国最优货币政策规则选择

金成晓，卢颖超

(1．吉林大学 数量经济研究中心，吉林 长春130012;2．吉林大学 商学院，吉林 长春130012)

新凯恩斯模型是当前宏观经济分析的一个主要工具，刻画了价格粘性等经济特征，主要用来描述经济增长与通货膨胀等变量之间的关系，但忽略了劳动力市场与失业率的刻画。然而失业率问题却一直是政策关注的焦点，所以将劳动力市场加入新凯恩斯模型来刻画我国通货膨胀率与失业率之间的关系非常必要。这种关系不仅可以用来刻画通货膨胀的短期动态特征，更是货币政策产生作用的理论基础。一国宏观经济政策的最终目标之间存在此消彼长的关系，如何进行权衡很难掌控，若使用相机抉择的政策往往会造成稳定性偏差等问题，所以货币政策操作需要遵循一定规则。本文拟权衡失业率与通货膨胀率来推导最优货币政策规则形式，并考量其对经济的作用效果。

一、文献综述

经济学家菲利普斯(Phillips)［1］最早提出了表示失业率与货币工资率之间交替关系的菲利普斯曲线。而后萨姆尔森(Samuelson)等［2］将菲利普斯曲线中的货币工资变动率替换为物价上涨率。而当前在宏观经济学界应用较广泛的新凯恩斯模型，却忽略了对劳动力市场的刻画，将其设置为完全竞争、工资灵活变动的形式［3］。在新凯恩斯模型中引入劳动力市场摩擦来研究通货膨胀与失业率之间的关系，目前主要有两种方法:应用较广泛的是将新凯恩斯模型与刻画劳动力市场的DMP模型［4］相结合，引入劳动力市场摩擦及工资粘性，对此，布兰查德(Blanchard)等［5－6］的研究具有代表性;另一种方法是基于加利(Gali)［7］在标准的新凯恩斯模型基础上重新对劳动力市场进行的解释，将工资设置为交错工资的形式，如埃尔采格(Erceg)等［8］的研究。由于当前失业率问题逐渐被提上日程，所以劳动力市场的问题应该得到充分的考虑。本文拟借鉴第一种对于劳动力市场的设定形式，在价格粘性与工资粘性的基础上研究通货膨胀与失业率之间的关系。

桑顿(Thornton)［9］、维克塞尔(Wicksell)［10］和弗里德曼(Friedman)［11］较早对货币政策规则进行了研究。当前学术界对于货币政策规则的刻画主要包括两种:一种为直接给定货币政策规则的形式，包括泰勒规则、弗里德曼规则等;另一种是在央行目标函数最优化基础上，推导出最优货币政策规则形式，对此，伍德福德(Woodford)［12］和埃里克(Eric)［13］的研究具有代表性。最优货币政策规则形式往往比较复杂，不适合在实践中应用，但最优货币政策规则相比于设定模型形式的规则具有更好的调控经济的作用以及更小的福利损失［14］。在我国，对于前者的研究较多，对于后者的研究也在不断地完善。刘斌［15］在混合菲利普斯曲线的基础上，研究了最优货币政策规则与泰勒规则相机抉择之间的相对福利损失以及通货膨胀的福利成本;艾宏德等［16］则在研究时更加突出了菲利普斯曲线对于最优货币政策的影响;张广现［17］论述了在传统框架及现代框架下的最优货币政策规则形式。上述研究基本上都是将经济增长与通货膨胀之间的权衡作为政策目标，而衡量失业率缺口与通货膨胀政策目标的在我国还少之又少。为此，本文拟借鉴前述研究成果，在具有微观基础的双粘性小型宏观经济模型基础上研究我国的最优货币政策规则形式。

二、模型构建

(一)基本模型设定

在本文的模型中不仅要加入价格粘性及工资粘性，同时还要对劳动力市场进行刻画，研究的侧重点为失业率与通货膨胀率。近年来国外就此进行的研究逐渐增多，如拉文纳(Ravenna)等［18］、卢卡(Luca)等［19］。本文参考布兰查德(Blanchard)等［5－6］的模型来设定IS曲线及菲利普斯曲线。

劳动市场的IS曲线表示为其中，u^t代表失业率对稳态的偏离值;πt代表失业率;it代表短期名义利率;r*t≡ρ－at+Et{at+1}为支持有效分配下的利率，ρ≡－logβ，β为跨期贴现因子，at代表生产力对其稳态的偏离。

表示通货膨胀率与失业率之间关系的菲利普斯曲线设定为:πt=－k u^

t+k(1－ δ)(1－x)u^t－1－ ψγat。其中，k≡αgMλ/δ(1－u)、ψ≡λΦ/(1－ βρa)≻0、λ≡(1－βθ)(1－θ)/θ、g≡Bxa、M=ε/(ε －1)、Φ≡MW/A=1－(1－β(1－δ))gM≺1及u=(δ(1－x))/(x+δ(1－x))均为深层次参数的组合，且 γ∈［0，1］，代表实际工资粘性参数;θ代表价格粘性参数;x代表劳动力市场紧度的稳态水平(工作发现率);ρa代表生产率冲击的持续性参数;δ∈(0，1)，为上一期雇佣工人在当期不在工作岗位工作比例;ε代表商品之间的替代弹性;B和α为雇佣成本函数中反应劳动力摩擦的两个常参数。

(二)最优货币政策规则求解

本文通过对央行的目标函数进行最优化来求解最优货币政策规则的形式，其中损失函数中关注通货膨胀和失业率的变动。在构建损失函数时参考刘斌［15］以及卢卡(Luca)等［19］的研究，将其设定如下:

其中，u^*、π*分别代表失业率缺口及通货膨胀率目标值;参数λ、ψ及υ代表在损失函数中央行对各目标变量的重视程度。

损失函数在IS曲线以及菲利普斯曲线的约束下，通过动态优化算法可以给出最优货币政策规则的形式。参考詹诺尼(Giannoni)等［20］的推导过程，其形式为:it=c1it－1+c2Et(it+1)+c3(u^t－u^*)+c4(πt－ π*)+c5(Et(πt+1)－π*)。

证明过程如下:首先给出拉格朗日函数

其中，ζt及ρt为拉格朗日乘子。然后分别对u^t、πt和it求一阶导数，则

最后消去两个拉格朗日乘子即可得到前述货币政策规则的形式。

在此利率规则中，利率除了受到其自身滞后及预期值的影响外，还受到失业率、通货膨胀的当期值以及通货膨胀预期值的影响。这种形式与美国2012年12月12日提出的伊文思规则形式十分相似。

三、实证分析

(一)数据选择及预处理

本文数据包括通货膨胀率和利率。本文中的通货膨胀率数据根据居民消费价格指数(CPI)计算得出，计算公式为通货膨胀率=CPI－100。由于数据序列为月度数据，所以本文使用Eviews软件通过月度平均的方法得到季度数据值。考虑到通货膨胀率数据受到季节因素的影响，所以对其进行季节调整。对于利率水平，选择中国人民银行对金融机构的三个月同业拆借利率的当期值来代表。样本数据的区间为1996年1季度到2013年3季度，数据来源为国家统计局网站及中经网数据库。

使用单位根的检验方法(ADF)对两个时间序列进行平稳性检验，发现两个变量的原序列在0．1的显著性水平下都平稳(见表1)，所以可以直接使用原序列进行实证部分的研究。

表1 单位根检验结果

(二)经济波动特征

本文所使用的模型是由劳动力市场的菲利普斯曲线、IS曲线以及最优货币政策规则三个方程构成了一个小型的宏观经济模型。本文采用贝叶斯方法对双粘性经济下的各种政策规则效果进行分析。其中9个参数采用校准的方式给出，其余5个参数进行估计。跨期贴现因子β参考李雪松等［21］的研究将其设置为0．99。众所周知，当经济处于稳定运行时期即一般均衡的时候，经济应该处于完全就业状态，所以失业率缺口u^*的值应设置为0。而对于我国通货膨胀目标值，本文则根据我国政府对2014年的工作报告中所给出的值设置为3．5%。雇佣成本函数中反应劳动力摩擦的两个常参数B、α和上一期雇佣工人在当期不在此工作岗位工作的比例δ参考布兰查德(Blanchard)等［5］的研究分别设置为0．11、1及0．12。损失函数的权重系数λ、ψ、υ的不同取值代表了货币当局的不同货币政策取向，本文为了突出对于失业率及通货膨胀率的权衡会对经济的福利损失造成不同影响，所以将其设定为两种情况加以分析，分别为1、0．5、0．1和0．5、1、0．1，分别代表政府对于失业率缺口、通货膨胀以及利率变动的不同重视程度。其余参数采用贝叶斯方法估计时，根据参数的取值范围分别对其进行先验分布设定，θ服从Beta(0．5，0．1)的分布，x服从Beta(0．7，0．5)，ε 服从Beta(0．6，0．5)，ρa服从Beta(0．5，0．2)分布，详见表2和表3。

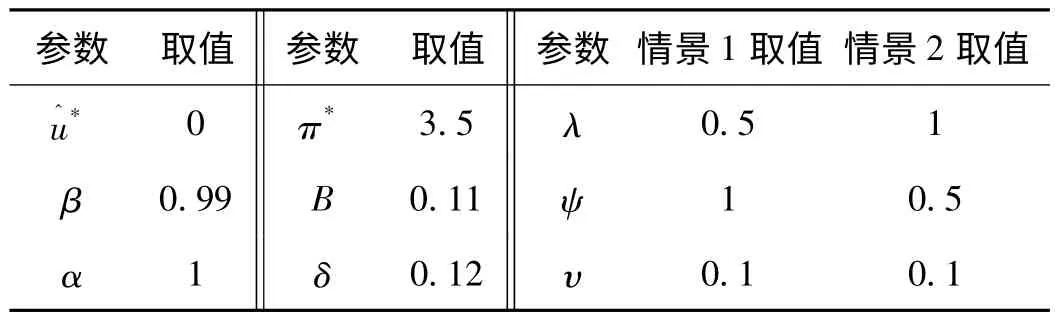
表2 参数校准

表3 先验及后验分布

从以上参数的后验估计值可知价格粘性系数为0．4936，代表每个时期都有49．36%的企业保持价格不变，而50．64%的企业会按照最优价格调整策略来调整当期的价格水平。而工资粘性的系数为0．5064，它也是取值在0－1之间，其值越大，代表劳动市场中工资的调整越缓慢，若取1则代表工资是刚性的，所以本文估计出的我国工资粘性系数为0．5046代表我国劳动力市场中工资的调整速度相对还是比较缓慢的。从结果可知，在我国的经济条件下，工资的粘性水平大于价格的粘性程度，所以在进行宏观分析的时候，忽略劳动力市场的粘性问题，将工资假定为灵活变动的情形与实际经济活动存在着较大的差距，而本文模型在构建中加入价格粘性的同时加入工资粘性更加符合现实经济条件。

图1所示分别代表在小型宏观经济模型中通货膨胀率、失业率缺口以及利率在三种货币政策规则下对于生产率冲击的反映情况。其中三种规则包括本文求出的最优利率规则以及分别将其去掉通货膨胀预期项和失业率缺口项的利率规则。第一行代表政策目标更加注重通货膨胀的稳定，将其权重系数设置为失业率缺口的二倍;第二行代表政策当局更加注重失业率缺口的稳定，将其权重系数设置为通货膨胀率系数的二倍。第一至三列分别代表通货膨胀率、失业率以及利率在三种不同货币政策规则下对生产率冲击的响应情况。首先横向对比各个变量的波动特征，当期初给定一单位正向生产率冲击时:通货膨胀上升，后逐渐下降，直至第5期下降到最低点后逐渐恢复稳态;同时失业率缺口上升，但其存在着滞后效应，当期失业率缺口上升较小，在滞后4期时达到最大水平，后逐渐下降恢复稳态水平，由于企业生产率的上升，在不增加总供给的情况下，雇佣工人的人数下降所以导致失业率上升;利率存在小幅下降后逐渐上升恢复稳态水平，由于生产率上升所以政府部门为了刺激生产，小幅下降利率。三个变量中幅度变化最大的为失业率缺口，并且三个变量的波动持续时间大致为15期左右。从三种政策规则的角度进行对比，当政策规则中不包含失业率缺口时，三种变量的波动幅度明显变大，所以加入失业率的货币政策对于经济具有更好的稳定效果，但是当政策中不包含通胀预期时，与我们所推出的最优货币政策规则下的变量波动效果非常接近，只是在波动的最后阶段有小幅偏离。综上所述，同时考虑通货膨胀预期及失业率作为阈值的利率规则具有更好的稳定经济效果以及前瞻性效果，若利率规则不考虑失业率或通货膨胀预期项都会使经济的波动偏离最优波动水平，使得经济的波动更大，失业率的影响效果明显。

图1 不同货币政策规则下变量的脉冲响应

表4 福利损失对比

(三)福利损失分析

此处给出在前述小型宏观经济模型中，权衡失业率缺口以及通货膨胀及预期的利率规则下，当政策目标的权重系数设定不同时福利损失的对比情况。福利损失使用各变量的方差来衡量，在前文估计的参数结果基础上，使用Dynare软件中的OSR工具箱进行计算，结果见表4。

从表4知，两种政策目标的情景下，完全承诺的最优货币政策规则的福利损失都是最小的，不包含失业率缺口的利率规则的福利损失最大，不包含通货膨胀预期项也使得福利损失上升，所以加入预期项使得政策规则更加具有前瞻性以及透明性的特点，其有助于稳定公众的预期，从而起到稳定经济的作用。加入通货膨胀预期以及失业率缺口的利率规则形式更适合应用于经济中。而纵向比较三种情景可见，更加关注失业率缺口稳定的政策相对于更加关注价格稳定的政策具有更大的福利损失。在两变量都处于合理区间时，通过损失一定的失业率来换取通货膨胀的稳定可以使得经济获得更大的福利。

(四)粘性系数的影响

本文还关注了价格粘性及工资粘性参数的改变对于经济中的主要变量的变动会造成怎样的影响，所以下文通过变换这两个参数的大小，给出经济在最优货币政策规则下的不同波动特征。价格粘性及工资粘性参数的贝叶斯后验估计值分别为0．4936和0．5064，那么我们考虑在前面给出的粘性参数的后验取值基础上，分别上调及下调一定的幅度，使其分别代表较低的粘性水平、中值的粘性水平以及较高的粘性水平。本文分别在给定两参数的取值为0．2，0．5及0．7的情况下对经济的波动特征进行模拟，以给出商品市场及劳动力市场的市场化程度对经济中主要变量的影响情况。此部分使用的货币政策规则为本文所求的最优利率规则，同时权衡失业率缺口、通货膨胀率以及其预期值。政策目标参数使用的是社会福利损失较小的组合(0．5，1，0．1)，即政府更加关注通货膨胀率的稳定，结果如图2所示。

图2中第一行与第二行分别代表当价格粘性及工资粘性参数发生变化时，三种变量对生产率冲击的波动特征。第一列至第三列分别代表通货膨胀率、失业率以及利率的波动特征。由图可知，价格粘性越小，三种变量对经济冲击的响应越剧烈;而当价格粘性变大时，变量的波动幅度变小。价格粘性越小说明商品市场中每期可以按照最优路径调整价格的厂商越多，所以价格波动越剧烈，市场中商品的供给与需求的波动越大，从而导致失业率以及利率更大的波动。而对于工资粘性来说，工资粘性参数越小，三种变量对经济冲击的响应幅度越小;而当工资粘性逐渐变大时，变量的波动幅度也随之增大。工资粘性越小，代表劳动力市场的摩擦越小，从而有越多的劳动者在当期可以得到最优的工资水平，因而相应的工作变动率就下降，失业率下降，导致商品市场中总供给与总需求不会发生较大的波动，所以通货膨胀率的波动较小，而由于经济的稳定，政策当局便无需用过度的调整工具变量来稳定经济，利率波动相对较小。

图2 不同粘性水平下变量的脉冲响应

(五)敏感性分析

考虑到在设定参数的先验分布时具有一定的主观性，所以敏感性检验非常必要。本文使用Dynare软件中的GSA工具箱给出参数的敏感性分析结果(见图3)。使用的检验方法参考马可(Marco)［22］的参数识别方法，敏感性分析采用MCF方法［23］。由结果可知，冲击的回归参数在模型估计的过程中识别能力较弱，其余参数具有较好的识别能力。且敏感性检验认为参数θ、ε、x的组合存在不确定性区间，并给出了相应的稳定取值区域以及不确定区域，其余参数的取值不影响模型的稳定性。由于本文中所设定的模型参数初始值都在稳定性取值区间范围内，所以以上的分析具有可信性。

图3 识别分析与敏感性分析结果

四、结论与政策建议

本文结合新凯恩斯模型与DMP模型，在经济框架中加入了劳动力市场，给出了加入劳动力市场后的菲利普斯曲线及IS曲线，同时加入价格粘性及工资粘性，而后通过动态优化方法推导出我国的最优货币政策规则形式，此利率规则将失业率缺口、通货膨胀率及预期值作为调控的阈值。通过构建我国的小型宏观经济模型，给出了不同经济变量在不同规则形式、不同政策目标下的波动特征。本文得出以下结论:

1．双粘性模型中，粘性价格参数的估计值为0．4936，说明每个季度大约有49．36%的企业选择不更新产品的价格，大约50．64%的企业会按照最优的方式来调整价格。而粘性工资参数的估计值为0．5064，劳动力市场中工资的调整相对比较缓慢。所以假定劳动力市场存在摩擦更加符合实际经济的特点。

2．将通货膨胀预期及失业率作为阈值的利率规则具有更好的稳定经济的效果，若利率规则不考虑失业率或通货膨胀预期，会使经济波动偏离最优水平，使得经济波动更大，失业率的影响效果明显，最优利率规则下的福利损失最小，不包含失业率缺口的利率规则的福利损失最大。由于就业与国计民生关系较为密切，所以政府在调控宏观政策时，其调控的下限不应仅关注经济增长目标，降低失业率也应得到充分的重视。不应光以GDP论英雄，经济增长应服务于民生的改善。通货膨胀预期作为政策调控的阈值，更加体现政策前瞻性及透明性的特点。

3．当政策目标更加关注通货膨胀率时，社会具有更小的福利损失。所以在两变量都处于合理区间时，通过损失失业率来换取通货膨胀的稳定可以使得经济获得更大的福利。

4．降低工资粘性及适度升高价格粘性有利于经济的稳定。所以政府应致力于降低劳动力市场的摩擦，降低工资调整成本等，同时充分发挥市场的调节作用。而价格粘性的上升短期内可能对于价格的稳定起到了一定的效果，但是长期仍应致力于提高经济的透明性，降低商品市场的摩擦，充分发挥市场调节作用，使得经济更加接近于最优路径运行。

［1］ PHILLIPS A W．The Relationship between Unemployment and the Rate of Change of Money Wages in the United Kingdom 1861－1957［J］．Economica，1958，100(25):283－299．

［2］ SAMUELSON PA，SOLOW R M．Analytical Aspects of Anti－Inflation Policy［J］．The American Economic Review，1960，50(2):177－192．

［3］ GALI J，SMETSF，WOUTERSR．Unemployment in an Estimated New Keynesian Model［R］．NBER Macroeconomics Annual，2011，26:329－360．

［4］ DALE M，PISSARIDESC．Job Creation and Job Destruction in the Theory of Unemployment［J］．Review of Economic Studies，1994，61:397－415．

［5］ BLANCHARD O，GALI J．A new Keynesian model with unemployment［R］．Working Paper Research，2006．

［6］ BLANCHARD O，GALI J．Labor Markets and Monetary Policy:A New－Keynesian Model with Unemployment［R］．NBER Working Papers，National Bureau of Economic Research，2008．

［7］ GALI J．Monetary policy and Unemployment［R］．NBER Working Papers，National Bureau of Economic Research，2010．

［8］ERCEG CJ，HENDERSON D W，LEVIN A T．Optimal monetary policy with staggered wage and price contracts［J］．Journal of Monetary Economics，2000，46(2):281－313．

［9］ THORNTON H．An enquiry into the nature and effects of the paper credit of great Britain［M］．London:Hatchard，1802:277－311．

［10］ WICKSELL K．The influence of the Interest rate on prices［J］．The Economic Journal，1907，17:213－220．

［11］ FRIEDMAN M．A monetary and fiscal framework for economic stability［J］．The American Economic Review，1948，38:245－264．

［12］ WOODFORD M．Interest and Prices［R］．Manuscript，Princeton University，2002．

［13］ ERICS．The Nonlinear Phillips Curve and Inflation Forecast Targeting:Symmetric versus Asymmetric Monetary Policy Rules［J］．Journal of Money，Credit and Banking，2004，36(3):361－386．

［14］ GIANNONI M P，WOODFORD M．Optimal Interest Rate Rules:General Theory［R］．NBER Working Paper，2003．

［15］ 刘斌．最优货币政策规则的选择及在我国的应用［J］．经济研究，2003(9):3－13．

［16］ 艾洪德，郭凯．混合预期增广的Phillips曲线与中国最优货币政策规则:基于SVAR模型的实证研究［J］．财经问题研究，2012(9):70－80．

［17］ 张广现．最优货币政策规则理论及其应用研究［D］．北京:首都经济贸易大学，2008．

［18］ RAVENNA E，WALSH C E．Welfare－Based Optimal Monetary Policy with Unemployment and Sticky Prices:A Linear－Quadratic Framework［J］．American Economic Journal，2011，3(2):130－162．

［19］ LUCA S，ULF S，ANTONELLA T．Monetary policy under uncertainty in an estimated model with labor market frictions［J］．Journal of Monetary Economics，2008，55(5):983－1006．

［20］ GIANNONI M P，WOODFORD M．Optimal Interest Rate Rules:General Theory［R］．NBER Working Paper，2003，No．9419．

［21］ 胡志鹏．中国货币政策的价格型调控条件是否成熟?:基于动态随机一般均衡模型的理论与实证分析［J］．经济研究，2012(6):60－72．

［22］ MARCO R．Algorithms for identification analysis under the DYNARE environment:final version of software［R］．Joint Research Centre，European Commission，2011．

［23］ MARCO R．Analysing DSGE Models with Global Sensitivity Analysis［J］．Computation Economic，2008，31:115－139．