盐岩流变损伤特性及本构模型研究

丁靖洋，周宏伟，陈 琼，刘 迪，刘建锋

（1.中国矿业大学(北京)煤炭资源与安全开采国家重点试验室，北京 100083；2.四川大学 水利水电学院，四川 成都 610065)

1 引言

随着中国经济的快速增长，能源问题日益受到各方重视，而战略能源储备则是保障能源安全的重要手段[1]。盐岩因其本身所具有的结构致密、低孔隙率、低渗透性等特点而成为地下储存硐室的理想围岩[2]，而针对硐室围岩长期流变特性及腔体长期稳定性的研究一直是重点及难点[3－4]。盐岩具有非常良好的流变特性，其典型的流变曲线可分为3个特征阶段：流变速率不断降低的衰减流变阶段；流变速率基本恒定的稳态流变阶段；流变速率不断增加的加速流变阶段，因此，建立能够描述盐岩流变全过程的数学本构模型尤其引起了国内外学者的关注[5]。总体而言，盐岩流变本构模型可以分为以下几类：经验模型[6－7]、元件模型[8－9]、损伤流变模型[10－12]及分数阶流变模型[13－14]等。元件模型因概念直观、意义明确而被大量应用，但大部分模型并不能描述岩石的加速流变阶段[15]。若从细观机制角度入手，分析岩石产生流变3个特征阶段的内在原因，并在此基础上构建流变本构模型，将更有助于模型对于宏观流变现象的描述。事实上，很多学者已经致力于构建宏观现象学与细观力学之间的桥 梁[16－17]，因此，针对盐岩流变过程中细观机制的研究，如微细观尺度上裂隙的发展及损伤的演化，是很有必要的。

分数阶微积分算法作为一种最近30年才在工程领域得到较广泛应用的理论[14]，其在描述非线性曲线特性方面具有强大的功能，如Xu 等[18]、Beda等[19]在分数阶模型的基础上对黏弹性材料进行了研究；Chen 等[20]、Fu 等[21]借助于分数阶微积分理论研究了离子的反常扩散现象。大量的盐岩流变曲线，尤其是加速流变阶段的曲线均表现出明显的非线性特性，因此，分数阶微积分理论无疑将成为构建流变本构模型的有力工具。Adolfsson 等[22]基于内变量理论构建了分数阶黏弹性本构模型；尹德顺等[23]基于分数阶微积分理论构建了一种软体元件，来描述介于理想固体与理想流体之间的“软物质”流变特性；周宏伟等[14,24]建立了一种新Abel 黏壶元件，通过将分数阶Abel 黏壶替代西原模型中Newton 黏壶的方法，构建了盐岩分数阶流变本构模型，并对该模型进行了无量纲化处理。本文在考虑流变过程中损伤演化机制的基础上，借助于盐岩流变-声发射试验，分析了流变3个特征阶段与声发射事件数的对应关系；基于声发射事件数构建了损伤变量随加载时间的函数关系式，并对关系式中的参数进行了敏感性分析；引入分数阶微积分理论，构建了盐岩流变损伤本构模型。研究结果表明，该本构模型能够很好地描述盐岩流变的3个特征阶段，尤其是加速流变阶段，且模型中参数意义较为明确，克服了纯粹经验模型及元件模型的诸多缺陷，将更有利于该本构模型对于盐岩流变特性的研究和描述。

2 盐岩流变-声发射试验及损伤模型的建立

2.1 盐岩流变-声发射试验分析

一般认为，当应力水平低于岩石屈服应力时，在流变试验中岩石将经历衰减、稳态流变阶段；当应力水平高于屈服应力时，岩石将经历衰减、稳态、加速3个流变阶段[25]。图1为文献[26]盐岩单轴流变-声发射试验结果，由图可以看出，整个试验过程可以分为3个阶段：第1 阶段对应流变曲线中的衰减流变阶段，在此阶段声发射事件数在逐渐减少，可以解释为在轴向应力加载的初期，盐岩发生了瞬时弹性应变以及随后的内部微裂隙的闭合。由于盐岩属于结晶沉积型岩石，内部晶粒排列致密[27]，因此，若将声发射事件数定义为盐岩内部微元体的破坏个数，则可以解释为随着盐岩内部结构致密性的增加，由于微元体破坏造成的损伤值在不断降低，此阶段可以理解为盐岩初始损伤的自愈合过程；第2阶段对应流变曲线中的稳态流变阶段，在此阶段声发射事件数处于一个较低水平且趋于平稳，可以解释为在轴向应力作用下，盐岩内部晶体由于发生黏弹性流动（如晶体位错、滑移）而进行了重新排布，在此阶段盐岩流变并无明显的损伤产生；第3 阶段对应流变曲线中的加速流变阶段，在此阶段声发射事件数呈现出明显的增大趋势，可以解释为随着加载时间的增长，盐岩内部产生了黏塑性流动，伴随着较多的微元体破坏及微裂隙的发育，在此阶段盐岩产生明显的损伤，因此，可以理解为损伤的发展是盐岩流变曲线出现加速流变阶段的内在原因。

图1 盐岩单轴流变试验中的声发射曲线[26]Fig.1 Curves of acoustic emission events for salt rock in uniaxial rheological test[26]

2.2 基于Weibull 分布的损伤表达式

岩石的声发射现象是其内部损伤演化的结果，因此，可利用损伤理论来建立基于声发射规律的模型[28]。对于单轴应力下的各向同性损伤，定义d为损伤变量，Kachanov 将其定义为即时承载面上微缺陷的总面积 Ad与无损时断面面积A 的比值。

假设断面微缺陷面积达到 Ad时的累积声发射事件数为N；断面面积A 完全破坏时，即岩石发生破坏时的累积声发射事件数为Nm，则

由式（1）、（2）可得

假设声发射事件数对应于盐岩内部微元体的破坏数，则基于细观损伤力学，假设损伤演化为一个随时间持续变化的过程，将岩石划分为若干个微元体，并假设微元体破坏的概率密度函数符合Weibull统计规律[29]，则可得

式中：m、n为表征损伤的参数，其取值大小受试验条件（如应力水平、温度等）及试件本身等因素影响。

在任意时刻t 内破坏的微元体个数为

式（5）为声发射事件数随加载时间的函数表达式。式中：Nm既为盐岩最终破坏时的累积声发射数（即破坏的总微元体数），也可视为与盐岩力学性质相关的参数。

加载至断面微缺陷面积达到 Ad时的微元体破坏总数为

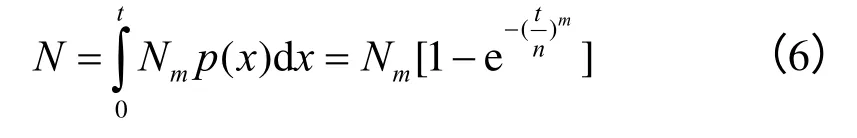
由式（3）可得损伤表达式为

式（7）为基于Weibull 分布的损伤表达式。

图2 声发射数据拟合Fig.2 Fitting and testing curves based on acoustic emission events

图2为基于式（5）拟合获得的盐岩声发射事件数-时间曲线，式中拟合参数分别为：m=16，n=60，Nm=20×106。通过与实际试验曲线对比可知，式（5）可以较真实地反映声发射事件数随时间的演化规律，从而证明了采用Weibull 分布作为概率密度函数的可取性。

图3 损伤变量曲线Fig.3 Curve of damage variable vs.time

将m=16，n=60 代入式（7），可得损伤变量随加载时间的演化曲线，如图3 所示，从图可以看出，损伤演化趋势与声发射曲线规律具有一致性，在加载初期损伤值较小，而当超过某个阈值之后，损伤迅速发展，伴随着声发射事件数的激增，直至盐岩试件最终发生流变破坏。

采用在德国进行的盐岩流变-超声波试验来验证式（7）的适用性。

超声波探伤试验被认为是研究岩石内部结构损伤演化的有效手段[30]，基于盐岩流变试验中的纵波波速（见图4），定义其损伤变量为[11]

式中：εv为体积应变；vp为纵波波速；v0为初始波速。

基于式（8）计算获得盐岩流变损伤变量值，并基于式（7）对图5 中的试验数值进行拟合，参数拟合结果为m=0.5，n=80 000。图5 拟合参数较图2 有一定差异，除了试样本身及应力水平、温度等的差异性，还与流变-超声波试验中，盐岩试件并未发生最终的流变破坏有关。但从拟合效果来看，式（7）对于流变-超声波试验同样具有适用性。m、n 与各影响因素之间具体的函数关系将是今后研究的重点。

图4 盐岩超声波试验数据Fig.4 Data of ultrasonic test on salt rock

图5 损伤变量拟合分析Fig.5 Data fitting of damage variable

2.3 参数m、n 敏感性分析

Weibull 分布中，m为表征概率密度函数曲线的形状参数，n为尺度参数，由本文上述分析可知，对于式（5）、（7），m、n为表征声发射事件数曲线形状的两个参数，也为表征损伤变量曲线形状的两个参数。对m、n 参数的敏感性分析曲线如图6、7 所示。

图6 不同m 值下的声发射曲线Fig.6 Curves of acoustic emission events with different values of m

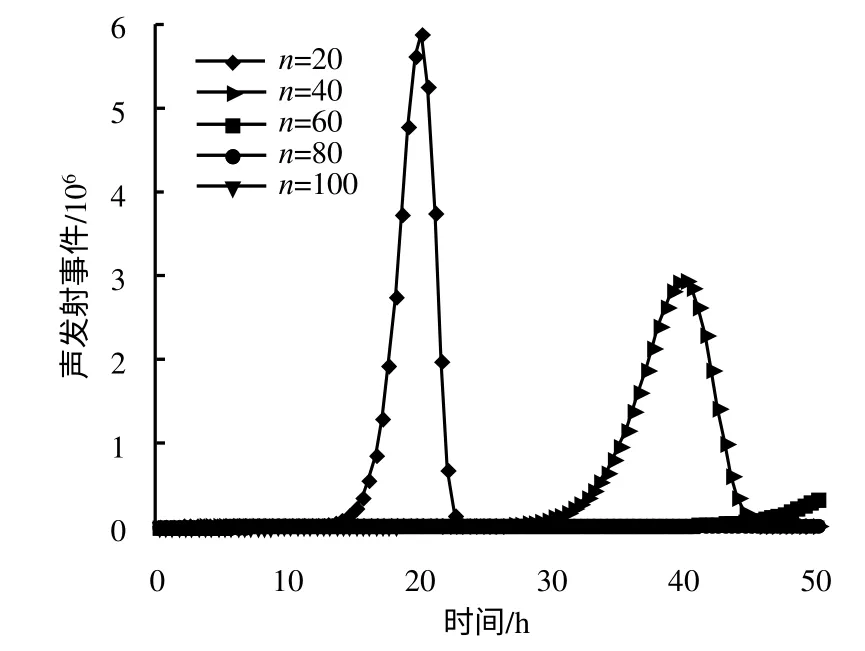
图7 不同n 值下的声发射曲线Fig.7 Curves of acoustic emission events with different values of n

由图可知，n 取定值，改变m 值大小（见图6），或者m 取定值，改变n 值大小（见图7），声发射事件数曲线差异性均较大。对于图6，m 值越大，其峰值点越晚出现，岩石经历的稳态流变阶段也就越长，越晚发生蠕变破坏；对于图7，n 值越大，其峰值点越低，声发射事件数达到峰值所需时间也越长，相同时间内损伤值也越小。这些特性反映了式（7）在描述损伤变量上的灵活性。

3 基于损伤的盐岩分数阶流变本构模型

Abel 黏壶本构模型表达式为

式（9）可写成如下形式：

西原模型是最能全面反映岩石弹-黏-塑性特性的力学模型，但并不能很好地描述岩石流变的全程曲线，尤其是加速流变阶段的曲线，如上文分析，岩石产生加速流变的内在原因是微裂隙的发展及损伤的积累，因此，若将损伤理论引入到本构模型的构建当中，并采用Abel 黏壶替代西原模型中的Newton 黏壶，则将更有利于该模型对于流变各阶段特性的描述。

基于损伤演化的盐岩分数阶流变本构模型如图8 所示，该模型由虎克体、黏弹性体、黏塑性体3部分串联而成，对应的3 部分应变分别为εe、εve及 εvp，则由组合元件原理，总应变ε为

图8 盐岩分数阶流变模型[14]Fig.8 Fractional rheological model of salt rock[14]

（1）εe表征的是加载一瞬间产生的瞬时弹性变形，本构关系为

式中：E0为虎克体的弹性系数。

（2）εve表征的是黏弹性变形，可以解释为盐岩内部较软弱部分由于黏弹性流动而产生的变形，此时盐岩内部并无明显的损伤产生[31]，采用Abel 黏壶元件替代黏弹性体中的Newton 黏壶元件，则可得

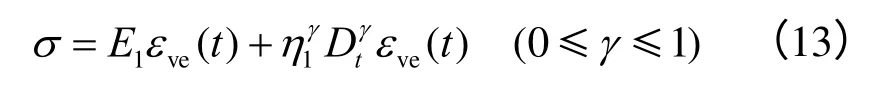
式中：E1为黏弹性体的弹性系数；为黏性系数。

求解式（13），可得[14]

（3）εvp表征的是黏塑性流动，可以解释为盐岩内部较坚硬部分由于微破裂及黏塑性流动而产生的变形，此时盐岩内部损伤开始积累并不断发展，直至达到某个阈值，盐岩发生流变破坏。受损伤演化影响，黏塑性体中Abel 黏壶的黏性系数将不再是一个常数，而将随流变时间的增加而不断衰减[32]，定义损伤与黏性系数的劣化关系满足下式：

将式（7）、（15）代入式（9），可得基于损伤的Abel 黏壶本构关系为

黏塑性体中，塑性元件应力 σp的表达式为

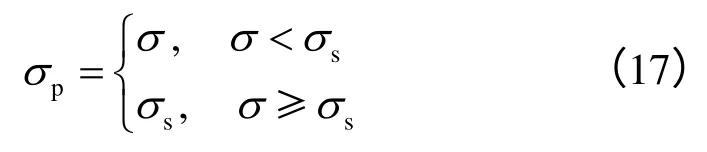
式中：σs为屈服应力。

由组合元件原理，可得

式中：σ为黏塑性体的总应力；σd为黏塑性体中Abel 黏壶的应力。

当σ＜ σs时，由式（17）、（18），可得 σd=0，即εvp=0。

当σ≥ σs时，由式（16），可得

由初值条件 εve(0)=0，Riemann-Liouville 分数阶导数与Caputo 分数阶导数之间可以相互转化，即，根据分数阶微分方程的求解方法[33]求解式（19）得

由式（12）、（14）、（20），考虑3 部分应变，可得基于损伤演化的盐岩分数阶流变本构模型为

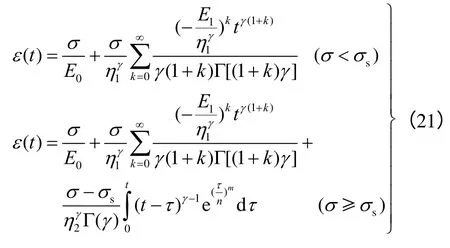
4 盐岩分数阶流变本构模型参数拟合

盐岩单轴流变试验采用四川大学程控流变试验仪，仪器参数为：单轴荷载为0～600 kN，围压为0～30 MPa，室验室恒温为22℃。盐岩样品选自湖北江汉油田王储1#，距地面约2 000 m。试件加工成高度为150 mm、直径为75 mm 的标准盐样共3件，编号为RS01a、RS02a、RS05a，如图9 所示。通过对比分析流变试验结果，选取3 阶段特征明显，具有代表意义的RS02a 试件流变曲线进行本构模型的参数拟合。RS02a 试件轴向荷载采用分级加载的方式，由σ=4 MPa 开始分10 级加载，每级增加2 MPa，加载至22 MPa，每级加载时间约为14 d。

图9 流变试验仪及盐岩试件Fig.9 Rheological apparatus and salt rock specimens

同时，对RS02a 试件加载前、后的内部结构进行了CT 扫描（如图10 所示），由对比可知，盐岩在流变过程中产生了明显的损伤：随着加载时间的进行，盐岩内部破裂单元个数逐渐增多，损伤不断积累，直至最终发生流变破坏。

采用最小二乘法拟合盐岩流变的全过程试验曲线，以此来确定本文提出的分数阶流变本构模型中的参数。做为对比，采用西元模型拟合获得的曲线也在图中同时给出。拟合曲线如图10 所示，参数拟合结果如表1 所示。

由图10 全过程流变试验曲线可知，RS02a 试件先后经历了衰减、稳态、加速3个阶段，且较西元模型，分数阶流变本构模型能更好地描述盐岩流变的3个特征阶段，尤其是加速流变阶段。

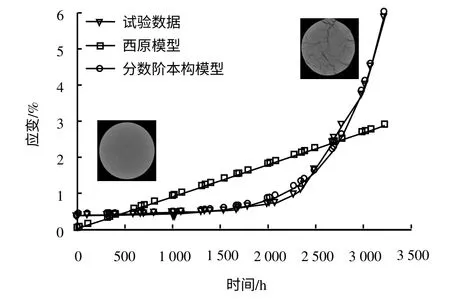
图10 试验数据与模型拟合效果对比Fig.10 Comparison between experimental data and fitting curves with constitutive model

表1 模型参数拟合结果Table 1 Parameters fitting of the model

式（22）为西原模型的流变本构模型，由此可知，西原模型实际上为本文构建的分数阶流变模型的一种特殊情况。

5 结论

（1）分析了盐岩流变-声发射试验各阶段的特性，在此基础上将声发射事件数定义为岩石内部微元体的破坏个数。通过假定微元体破坏的概率密度函数满足Weibull 统计规律，获得了声发射事件数、损伤变量随加载时间的函数表达式。

（2）通过拟合盐岩流变-声发射试验数据、盐岩流变-超声波试验数据，验证了声发射事件数、损伤变量函数表达式的合理性及适用性，并对表达式中的形状参数m、尺度参数n 进行了敏感性分析，揭示了m、n 与声发射事件数及损伤值的关系。

（3）基于分数阶微积分理论及损伤理论，通过定义损伤与流变系数之间的劣化关系式，获得基于损伤的Abel 黏壶函数表达式，并在西原模型的基础上，求解获得基于损伤的盐岩分数阶流变本构模型。通过与西原模型的对比发现，本文提出的本构模型能更好地反映盐岩流变的3个阶段特性，尤其是加速流变阶段特性，且验证了西原模型为该本构模型的一个特殊形式。

[1]周宏伟,王春萍,丁靖洋,等.盐岩流变特性及盐腔长期稳定性研究进展[J].力学与实践,2011,33(5):1－7.ZHOU Hong-wei,WANG Chun-ping,DING Jing-yang,et al.Developments in researches on time-dependent behavior of salt rock and long-term stability of salt cavity[J].Mechanics in Engineering,2011,33(5):1－7.

[2]刘江,杨春和,吴文,等.盐岩蠕变特性和本构关系研究[J].岩土力学,2006,27(8):1267－1271.LIU Jiang,YANG Chun-he,WU Wen,et al.Study on creep characteristics and constitutive relation of rock salt[J].Rock and Soil Mechanics,2006,27(8):1267－1271.

[3]杨文东,张强勇,陈芳,等.基于压缩蠕变试验的流变参数理论解析反演[J].力学学报,2012,44(3):638－642.YANG Wen-dong,ZHANG Qiang-yong,CHEN Fang,et al.Rheological parameters inversion by theoretical analysis of compressive creep test[J].Chinese Journal of Theoretical and Applied Mechanics,2012,44(3):638－642.

[4]张梅花,高谦,翟淑花.高地应力围岩流变特性及竖井长期稳定性分析[J].力学学报,2010,42(3):474－481.ZHANG Mei-hua,GAO Qian,ZHAI Shu-hua.Study on creep properties of rocks and long-time stability of shaft in high ground stress zone[J].Chinese Journal of Theoretical and Applied Mechanics,2010,42(3):474－481.

[5]URAI J L,SPIERS C J,HENDRIK H J,et al.Weakening of rock-salt by water during long-term creep[J].Nature,1986,324:554－557.

[6]CARTER N L,HORSEMAN S T,RUSSELL J E.Rheology of salt rock[J].Journal of Structural Geology,1993,15(10):1257－1272.

[7]YANG C H,DAEMEN J K,YIN J H.Experimental investigation of creep behavior of salt rock[J].International Journal of Rock Mechanics and Mining Sciences,1999,36(2):233－242.

[8]王军保,刘新荣,郭建强,等.盐岩蠕变特性及其非线性本构模型[J].煤炭学报,2014,39(3):445－451.WANG Jun-bao,LIU Xin-rong,GUO Jian-qiang,et al.Creep properties of salt rock and its nonlinear constitutive model[J].Journal of China Coal Society,2014,39(3):445－451.

[9]胡其志,冯夏庭,周辉.考虑温度损伤的盐岩蠕变本构关系研究[J].岩土力学,2009,30(8):2245－2248.HU Qi-zhi,FENG Xia-ting,ZHOU Hui.Study of creep model of rock salt with thermal damage considered[J].Rock and Soil Mechanics,2009,30(8):2245－2248.

[10]CHAN K S,BODNER S R,FOSSUM A F,et al.A damage mechanics treatment of creep failure in rock salt[J].International Journal of Damage Mechanics,1997,6(1):121－152.

[11]HOU Z.Mechanical and hydraulic behavior of rock salt in the excavation disturbed zone around underground facilities[J].International Journal of Rock Mechanics and Mining Sciences,2003,40(5):725－738.

[12]WANG G J.A new constitutive creep-damage model for salt rock and its characteristics[J].International Journal of Rock Mechanics and Mining Sciences,2004,41(Supp.1):61－67.

[13]ZHOU H W,WANG C P,HAN B B,et al.A creep constitutive model for salt rock based on fractional derivatives[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(1):116－121.

[14]周宏伟,王春萍,段志强,等.基于分数阶导数的盐岩流变本构模型[J].中国科学:物理学 力学 天文学,2012,42(3):310－318.ZHOU Hong-wei,WANG Chun-ping,DUAN Zhi-Qiang,et al.Time-based fractional derivative approach to creep constitutive model of salt rock[J].Scientia Sinica Physica,Mechanica &Astronomica,2012,42(3):310－318.

[15]李良权,徐卫亚,王伟.基于西原模型的非线性黏弹塑性流变模型[J].力学学报,2009,41(5):671－680.LI Liang-quan,XU Wei-ya,WANG Wei.A nonlinear viscoelastoplastic rheological model based on Nishihara’s model[J].Chinese Journal of Theoretical and Applied Mechanics,2009,41(5):671－680.

[16]BAZANT Z P,XI Y.Drying creep of concrete:Constitutive model and new experiments separating its mechanism[J].Materials and Structures,1994,27:3－14.

[17]TANG S,GREENE M S,LIU W K.Two-scale mechanism-based theory of nonlinear viscoelasticity[J].Journal of the Mechanics and Physics of Solids,2012,60(2):199－226.

[18]XU M Y,TAN W C.Intermediate processes and critical phenomena:Theory,method and progress of fractional operators and their applications to modern mechanics[J].Science in China(Series G),2006,49(3):257－272.

[19]BEDA T,CHEVALIER Y.New methods for identifying rheological parameter for fractional derivative modeling of viscoelastic behavior[J].Mechanics of Time-Dependent Materials,2004,8:105－118.

[20]CHEN W,ZHANG J J,ZHANG J Y.A variable-order time-fractional derivative model for chloride ions sub-diffusion in concrete structures[J].Fractional Calculus and Applied Analysis,2013,16(1):76－92.

[21]FU Z J,CHEN W,YANG H T.Boundary particle method for Laplace transformed time fractional diffusion equations[J].Journal of Computational Physics,2013,235:52－66.

[22]ADOLFSSON K,ENELUND M,OLSSON P.On the fractional order model of viscoelasticity[J].Mechanics of Time-Dependent Materials,2005,9:15－34.

[23]殷德顺,任俊娟,和成亮,等.一种新的岩土流变模型元件[J].岩石力学与工程学报,2007,26(9):1899－1903.YIN De-shun,REN Jun-juan,HE Cheng-liang,et al.A new rheological model element for geomaterials[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(9):1899－1903.

[24]ZHOU H W,WANG C P,L.Mishnaevsky J,et al.A fractional derivative approach to full creep regions in salt rock[J].Mechanics of Time-Dependent Materials,2013,17(3):413－425.

[25]陈文玲,赵法锁,弓虎军.三轴蠕变试验中云母石英片岩蠕变参数的研究[J].岩石力学与工程学报,2011,30(增刊1):2810－2816.CHEN Wen-ling,ZHAO Fa-suo,GONG Hu-jun.Study of creep parameters of mica-quartzose schist during triaxial creep test[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(Supp.1):2810－2816.

[26]STEAD D,SZCZEPANIK Z.Time-dependent acoustic emission studies on potash[C]//Proceedings of 32ndU.S.Rock Mechanics Symposium.Oklahoma:[s.n.],1991:471－479.

[27]姜德义,陈结,任松,等.盐岩单轴应变率效应与声发射特征试验研究[J].岩石力学与工程学报,2012,31(2):326－336.JIANG De-yi,CHEN Jie,REN Song,et al.Experimental study of strain rate effect and acoustic emission characteristics of salt rock under uniaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(2):326－336.

[28]张明,李仲奎,杨强,等.准脆性材料声发射的损伤模型及统计分析[J].岩石力学与工程学报,2006,25(12):2493－2501.ZHANG Ming,LI Zhong-kui,YANG Qiang,et al.A damage model and statistical analysis of acousticemission for quasi-brittle materials[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(12):2493－2501.

[29]丁靖洋,周宏伟,李潮,等.基于Weibull 分布的盐岩分数阶蠕变本构模型研究[J].固体力学学报,2013,34(5):473－480.DING Jing-yang,ZHOU Hong-wei,LI Chao,et al.The fractional derivative approach to creep constitutive model of salt rock based on Weibull distribution[J].Chinese Journal of Solid Mechanics,2013,34(5):473－480.

[30]KRISHNAN B,JITENDRA S V,RAGHU V P.Creep damage characterization using a low amplitude nonlinear ultrasonic technique[J].Materials Characterization,2011,62(3):275－286.

[31]徐卫亚,周家文,杨圣奇,等.绿片岩蠕变损伤本构关系研究[J].岩石力学与工程学报,2006,25(增刊1):3093－3097.XU Wei-ya,ZHOU Jia-wen,YANG Sheng-qi,et al.Study on creep damage constitutive relation of greenschist specimen[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(Supp.1):3093－3097.

[32]陈卫忠,王者超,伍国军,等.盐岩非线性蠕变损伤本构模型及其工程应用[J].岩石力学与工程学报,2007,26(3):467－472.CHEN Wei-zhong,WANG Zhe-chao,WU Guo-jun,et al.Nonlinear creep damage constitutive model of rock salt and its application to engineering[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(3):467－472.

[33]KILBAS A A,SRIVASTAVA H M,TRUJILLO J J.Theory and applications of fractional differential equations[M].Amsterdam:Elsevier,2006.