基于数字图像相关方法的等应变率下不同含水率砂样剪切带观测

王学滨，杜亚志，潘一山，顾 路

（1.中国地震局地质研究所 地震动力学国家重点实验室，北京 100029；2.辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000；3.辽宁工程技术大学 计算力学研究所，辽宁 阜新 123000）

1 引言

孔隙水或流体的存在，对于固体局部化过程的影响一般不容忽视。一些地质灾害的发生和孔隙流体与固体的复杂相互作用密不可分，雨季滑坡、砂土液化、油井抽注水地震、水库地震、煤和瓦斯突出都是常见的例子[1－4]。在煤炭开采中，伴随着煤体的变形破坏，高孔隙压力的瓦斯会聚集在有限的区域之内，煤体变形局部化和瓦斯孔隙压力局部化现象共存，一旦条件满足，就可能形成煤和瓦斯突出灾害，在煤体中形成突出孔洞[5－6]。众所周知，孔隙水或流体对固体变形破坏的影响体现在多方面，从宏观角度，采用力学方法研究孔隙流体的影响时，可通过引入达西渗流定律、有效应力定律、固结方程、水致弱化函数等途径实现，以考虑流体在固体骨架之间的渗流、孔隙压力的扩散及固体力学性能的降低等因素。

目前，在水-土耦合局部化研究方面，已有不少数值模拟研究开展[1－4,7－12]，但相比之下，相应的试验研究还不多见。客观地讲，许多数值模拟研究的目的主要在于定性分析，一些参数的演变规律不易于获取或取值欠缺理论依据，相应的数值结果缺乏全方位的试验验证。但这并不妨碍对剪切带形成过程中一系列复杂现象的定性认识和理解，例如，剪切带内外应力、应变、孔隙压力、孔隙比等演变规律的差异，剪胀、负孔压与应变软化的关系等。

关于砂样局部化问题的认识，目前多是针对某种砂样在不同加载条件下获取的，例如，针对干砂、饱和砂、松砂、密砂、超固结砂开展研究，通过改变加载条件，以研究围压、应变率的影响。尽管目前关于含水率对岩土材料宏观力学性能的影响已知之甚多，但对于剪切带及应变场的影响还少见报道。

在压缩位移控制加载条件下，利用自主开发的基于粒子群优化的数字图像相关（digital image correlation,DIC）方法，本文开展了不同含水率（12.7%～16.5%）砂样应变场观测研究，分析了最大剪切应变的时空分布规律，还研究了子区尺寸对砂样不同位置最大剪切应变演变规律的影响。

2 数字图像相关方法简介

DIC 方法是岩土材料剪切带观测的一种重要手段[13－18]。本文DIC 方法系自主研发，是多种相关搜索方法的有机集成，适于坚硬材料（例如岩石、混凝土等）和相对比较软弱材料（例如砂土、相似材料等）的变形场观测研究。在进行相关搜索时，在传统N-R（Newton-Raphson）迭代方法的基础上，引入了群智能的粒子群优化（particle swarm optimization,PSO）算法，试图避免N-R 迭代方法易于陷入局部最优和迭代初值不易确定的弊端。

上述方法可以选择全量或增量方式进行计算。所谓全量方式是指以第1 张散斑图作为基准，计算出的随后图片的位移和应变都是相对第1 张图片的。所谓增量方式是指以前一张图片作为基准，计算出的后一张图片的位移和应变是相对于前一张的。采用全量方式计算时，当位移和/或应变较大时，可将前一张图片的位移和应变作为后一张图片位移和应变的初值。

3 试验过程及结果分析

3.1 试验步骤

长方体砂样的制备经历了将砂块碾碎、过筛、掺水、搅拌、浇注、振捣、静置、切割等过程，与文献[17]所述相同，试验条件与之有所不同。本文中，利用DLY-60 型微机控制电液伺服试验机对30余个不同含水率砂样进行了单向压缩位移控制加载（见图1(a)），加载速率为5 mm/min，在试验过程中，利用数码相机连续拍摄砂样的一个最大表面的散斑场，砂样无侧压，外侧无膜包裹。具有相同含水率的砂样准备3～5个。图1(b)、1(c)仅给出了21#砂样在加载初期及后期的散斑图。砂样的纵向应变εa是根据加载速率和加载时间计算得到的；砂样端部的压应力σa是试验机输出的。此外，根据有关规范，本文还对砂样的粒径级配进行了测试，结果见表1。限于篇幅，本文仅重点分析了3个砂样（8#、21#和22#）的观测结果，含水率保持适中，均未达到饱和状态（见表2），含水率高的砂样饱和度也高。砂土的比重Gs=2.66[18]，通过计算可得8#、21#及22#砂样的孔隙比分别为0.5、0.61 及0.46。

图1 试验砂样和散斑图Fig.1 Sand specimens and speckle images

表1 砂样的颗粒直径分布Table1 Distribution of sand grain diameters

3.2 测点布置及计算

从拍摄的大量图片中，仅选择有代表性的来计算测点的位移场，对于8#、21#及22#砂样，选择的用于计算的图片分别为16、17 及13 张。通过对位移场进行中心差分获取最大剪切应变γmax[12]。对选择的图片重新进行编号，砂样在未加载时拍摄的一张图片被选作参考图像，编号为0，其余选择的图片的编号从1 开始，依次排列。在计算测点的位移场时，采用先粗后细的相关搜索方法[17]。

在本文中，获取的应变场是全量，即是相对于参考图像的，用0-选择图片的编号标明。参考图像上的测点等间隔布置，呈43 行25 列。

图2～4 分别给出了3个砂样在6个不同时刻的γmax的分布规律，图中下方的数字表示列数，左面的数字表示行数。在每个砂样中设置了4个测点，由下到上分别为A～D，其位置在图中用黑色小圆点标明。仅在图2(a)、3(a)、4(a)中标明了这些测点。子区尺寸取为31×31 像素。

图5 给出了3个砂样的压应力σa-纵向应变εa曲线和每个砂样中测点A～D 的γmax的演变规律。在图5(a)、5(d)、5(g)中，子区尺寸取为11×11 像素，在图5(b)、5(e)、5(h)中，子区尺寸取为21×21 像素，在图5(c)、5(f)、5(i)中，子区尺寸取为31×31 像素。也就是说，图2～4 中每个砂样的4个测点的γmax的演变规律位于图5 中第3 列，分别对应图5(c)、5(f)、5(i)。图2～4 中的6个时刻与图5 中的6个数据点相对应。

表2 砂样的基本参数及加载时间Table2 Basic parameters and loading times for specimens

图2 21#砂样（含水率为16.5%）最大剪切应变分布的演变Fig.2 Evolution of the maximum shear strain of sand specimen#21 with water content of 16.5%

图3 8#砂样（含水率为13.8%）最大剪切应变分布的演变Fig.3 Evolution of the maximum shear strain of sand specimen#8 with water content of 13.8%

图4 22#砂样（含水率为12.7%）最大剪切应变分布的演变Fig.4 Evolution of the maximum shear strain of sand specimen#22 with water content of 12.7%

3.3 σa-εa曲线

由图5(a)、5(d)、5(g)可以发现，21#和8#砂样的σa-εa曲线经历了两个不同的阶段：近似线性阶段和硬化阶段；而22#砂样除了经历上述两个阶段，还经历了微弱的软化阶段。经过测量，21#、8#及22#砂样的弹性模量分别为1.8、6.8、7.4 MPa。由此可以发现，随着含水率的减小，弹性模量升高。

在图5(a)、5(d)、5(g)中，还给出了σa-εa曲线上最后一点所对应的散斑图，从中可以观察到砂样内部出现了为数不多的宏观剪切裂纹；砂样的侧向变形不均匀，总体上呈鼓形。

3.4 观测平面内γmax的分布及演化规律

图2(a)、3(a)、4(a)的σa均在近似线性阶段，此时，砂样上半部分的γmax相对较高，而下半部分的γmax较低，这与砂样上端面受压头向下驱动且下端面不动有关。砂样上半部分发生显著的纵向压缩和侧向膨胀。总体上，γmax的值并不高，在～10-2量级。砂样下半部分的γmax等值线图比较斑驳，反映了这一部分的γmax小，其结果会在一定程度上受标准偏差的影响。

图2(b)～2(f)、3(b)～3(f)、4(b)～4(f)的σa处于硬化阶段，随着εa的增加，γmax的高值区由分散变集中，剪切带（或称之为剪切应变局部化带）的长度有所增加，宽度有所降低。剪切带似乎有多条，但难于分清彼此。

需要指出的是，图2(f)、3(f)、4(f)之后的σa处于硬化或软化阶段，本文未给出γmax的结果，这是由于在图2(f)、3(f)、4(f)稍后，从拍摄的图片中已可观察到呈黑色的细微裂纹。此时，使用剪切带的概念有失准确。

在微裂纹出现稍前（见图2(f)、3(f)、4(f)），强烈的剪切应变仅集中在少量的剪切带上，特别是在22#砂样中（见图4(f)），在该砂样内部可见一条较短的剪切带，这一位置即将出现微裂纹。在8#砂样中，可以观察到1 条通过砂样右上角的较长的剪切带（见图3(f)）。在21#砂样中，γmax的集中程度不如8#及22#砂样，高值区多且分散（见图2(f)）。

通过上述分析，可以发现，提高含水率，应变集中区域变广（反映了剪切带数量变多），但应变集中程度变弱，较好地反映了砂样塑性增强的特点。

3.5 测点γmax的演变规律

由图5(c)、5(f)、5(i)可以发现，随着砂样εa的增加，各测点的γmax的增加方式有所不同。有的表现为线性增加，而有的则表现为快速增加，致使γmax-εa曲线呈现上凹的特点。下面，具体研究不同位置测点的γmax的演变规律。

对于22#砂样，测点A 位于低γmax区，离砂样的下端面最近。测点B、C、D 均位于砂样的上半部分。测点B 靠近砂样的纵向对称线，而测点D 位于砂样的左上角附近。由图4(a)、4(f)可以发现，测点C恰位于那条较短的剪切带上。由图5(i)可以发现，随着εa的增加，测点A 的γmax呈线性变化，这与测点A 位于砂样的应变高值区之外有关；测点A 的γmax在测点B、C、D 的γmax的下方。随着εa的增加，测点B、C、D 的γmax均呈非线性变化，这与这些测点的位置有关。当εa＜0.05 时，测点B、C、D 的γmax差别不大；而当εa≥0.05 时，测点C 的γmax快速增加，这反映了剪切带的形成，但测点B、D 的γmax仍然差别不大。

对于8#砂样，测点A 位于砂样的应变高值区之外（见图3(a)、3(f)），离砂样下端面最近，随着εa的增加，γmax呈线性方式增加，且γmax的值较低（见图5(f)）。测点D 位于砂样的左上角附近，其γmax比A 测点的高，随着εa的增加，γmax呈近似线性方式增加。测点B、C 的γmax高于测点D。当εa＜0.06 时，测点B、C 的γmax差别不大；但当εa≥0.06 时，测点C 的γmax快速增加，反映了通过砂样右上角的剪切带的形成。

对于21#砂样，各测点的γmax随εa的增加均以非线性方式快速增加（见图5(c)）。这与该砂样的含水率高有关。测点B 的γmax一直较高，该测点大致位于砂样的纵向对称轴上（见图2(a)），而测点A 的γmax一直最低，这与该测点离砂样下端面最近有关。

通过上述分析可以发现，位于应变高值区和低值区的测点的γmax的演变规律差别较大，前者随εa增加呈非线性方式快速增加，而后者随εa增加一般呈线性方式增加。当εa不高时，位于应变高值区内部的测点的γmax差别可能并不大，但当εa较高时，一些测点的γmax会急剧增加，反映了剪切带的形成。而临近砂样下端面的测点的γmax一直相对较低。含水率较高时，不同测点的γmax均呈非线性方式快速增长。

3.6 测线上γmax的分布及演变规律

从图2～4 中，并不易清晰地观察到γmax在某些剖面上的分布及演变规律。为此，将图2～4 中的部分数据提取出来，绘于各自的图中。限于篇幅，在图6 中仅给出了列数为13 时γmax的分布规律，由此可以发现：

（1）当γmax处于非均匀分布阶段时，含水率较低的22#砂样γmax的分布表现为峰值小，高值区所占尺寸或面积小的特点，而含水率较高的21#砂样表现为峰值多，高值区所占面积大的特点。这说明，相对干的砂样中剪切带的数量少。

（2）22#、8#及21#砂样微裂纹出现稍前的γmax分别为0.55、0.5 及1。应当指出，这仅是根据第13列数据得到的结果。对于第7 列数据，上述3个砂样微裂纹出现稍前的γmax分别为0.5、0.4 及0.5。对于第19 列的数据，上述3个砂样微裂纹出现稍前的γmax分别为0.7、0.7 及0.75。由此可以发现，相对干的砂样微裂纹出现稍前的γmax一般较小。

（3）尽管图6 中3个砂样的结果存在上述两点差别，但具有下列共性：砂样下端附近的三角形区域的γmax较低，而加载端附近的上三角区域的γmax要高一些。因而，图6 各子图看起来并不严格左右对称，而是左半部分较陡，而右半部分较缓。

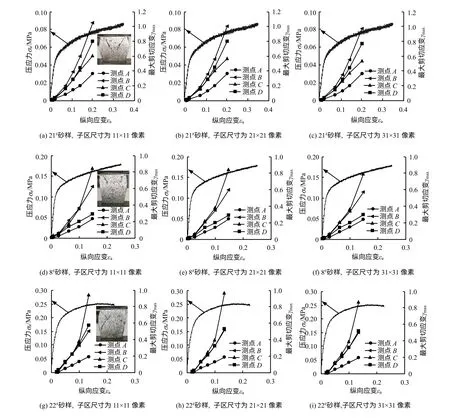
图5 砂样的压应力σa-纵向应变εa曲线及不同位置测点的最大剪切应变γmax的演变规律以及子区尺寸的影响Fig.5 Compressive stress(σa)-longitudinal strain(εa)curves of sand specimens,evolution of the maximum shear strains(γmax)for different monitoring points,and influence of the size of subset

图6 砂样纵向对称线附近最大剪切应变γmax的分布规律Fig.6 Distributions of the maximum shear strain(γmax)in vicinity of longitudinal symmetric lines of sand specimens

图7 砂样纵向对称线附近最大剪切应变γmax的分布规律Fig.7 Distributions of maximum shear strains(γmax)in vicinity of longitudinal symmetric lines of sand specimens

图8 子区尺寸对微裂纹出现稍前的测点的最大剪切应变γmax的影响Fig.8 Effects of size of subset on maximum shear strains(γmax)for different monitoring points before microcracks initiating

将εa=0.04 及0.1 时3个砂样第13 列数据叠加在图7 中。由图可以发现，与上文中同样的现象：①含水率高的砂样，γmax的高值区分布宽广；②含水率高的砂样，微裂纹出现稍前的γmax较高。除此之外，还可以发现：当εa=0.04 及0.1 时，在γmax-行数曲线的左半部分，含水率高的结果通常高。但在右半部分，当εa=0.04 时，含水率中等的砂样的结果反而最高。当εa=0.1 时，并不能发现明显的规律。上述反常，至少在第7、19 列数据中亦可发现。或许可采用下述两点解释上述反常：①不同砂样在制备过程中不可避免存在细微差别；②不同砂样中剪切带位置不同。

3.7 子区尺寸的影响

在保证子区正确匹配的前提下，研究子区尺寸的影响是有意义的。本文所采用的子区之间匹配的相关系数公式为1 相关[17]。

通过分析图5 中子区尺寸不同条件下的γmax的演变规律可以发现下列现象：①对于大多数点而言，子区尺寸基本不影响γmax，这与γmax的分布比较均匀有关，例如22#砂样中测点A，见图5(g)～5(i)；②随着子区尺寸的增加，γmax下降，例如22#砂样中测点D，见图5(g)～5(i)。

22#砂样中测点D 位于微裂纹出现稍前的剪切带上（见图4），带内具有较高的应变梯度。当子区尺寸变大时，子区会涵盖剪切带外的一部分低应变区。因此，当子区尺寸增加时，某些测点的高应变会被低估。相反，当子区尺寸增大时，若涵盖了γmax高值区的一部分，就可能高估某些测点的应变。

由图5 还可以发现，当εa不同时，子区尺寸对γmax的影响程度并不相同。当εa较小时，影响小；而当εa较大时，影响大。

在图8 中给出了微裂纹出现稍前（21#、8#及22#的εa分别为0.20、0.15 及0.14）12个测点的γmax随子区尺寸的演变规律。由此可以发现下列3 种现象：①子区尺寸基本不影响γmax，例如图8(a)、8(c)中测点A 的结果，这与γmax的值低且分布较均匀有关；②随着子区尺寸的增加，γmax下降，例如图8(a)中测点C 的结果，图8(b)中测点B 的结果和图8(c)中测点D 的结果，这与子区尺寸增大后涵盖了一部分低应变区有关；③随着子区尺寸的增加，γmax变化复杂，有的先升后不变，例如图8(b)中测点A和图8(c)中测点B 的结果，有的先升后降，例如（图8(b)、8(c)中测点C 的结果）等。

4 结论

（1）随着含水率的增加，微裂纹出现变晚，微裂纹出现稍前的最大剪切应变提高，最大剪切应变高值区分布变宽（反映了剪切带的条数变多），变形相对更加均匀，反映了砂样塑性的增强。

（2）在砂样的不同位置，随着纵向应变的增加，最大剪切应变的演变规律不同。在应变高值区，最大剪切应变以非线性方式快速增加；在应变低值区，最大剪切应变一般以线性方式增加。

（3）当剪切带出现以后，子区尺寸对最大剪切应变有明显的影响。增加子区尺寸，最大剪切应变升降不定，关键取决于测点所处的位置。

[1]LORET B,PREVOST J H.Dynamic strain localization in fluid-saturated porous media[J].Journal of Engineering Mechanics,ASCE,1991,117(4):907－922.

[2]LARSSON R,RUNESSON K,STURE S.Embedded localization band in undrained soil based on regularized strong discontinuity—theory and FE-analysis[J].International Journal of Solids and Structures,1996,33(20－22):3081－3101.

[3]OKA F,ADACHI T,YASHIMA A.A strain localization analysis using a viscoplastic softening model for clay[J].International Journal of Plasticity,1995,11(5):523－545.

[4]尹光志,赵洪宝,许江,等.煤与瓦斯突出模拟试验研究[J].岩石力学与工程学报,2009,28(8):1674－1680.YIN Guang-zhi,ZHAO Hong-bao,XU Jiang,et al.Experimental study of simulation of coal and gas outburst[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(8):1674－1680.

[5]蒋承林.煤壁突出孔洞的形成机理研究[J].岩石力学与工程学报,2000,19(2):225－228.JIANG Cheng-lin.Study of forming mechanism of outburst hole[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(2):225－228.

[6]黄茂松,钱建固,吴世明.饱和土体应变局部化的复合体理论[J].岩土工程学报,2002,24(1):21－25.HUANG Mao-song,QIAN Jian-gu,WU Shi-ming.A homogenization approach to localized deformation in saturated soils[J].Chinese Journal of Geotechnical Engineering,2002,24(1):21－25.

[7]徐连民,王兴然.用有限变形理论研究黏性土试样中变形的局部化问题[J].岩土工程学报,2004,26(2):225－228.XU Lian-min,WANG Xing-ran.Numerical simulation of shear band in clayey soils using finite deformation theory[J].Chinese Journal of Geotechnical Engineering,2004,26(2):225－228.

[8]甄文战,孙德安,段博.不同应力路径下超固结黏土试样变形局部化分析[J].岩土力学,2011,32(1):293－298.ZHEN Wen-zhan,SUN De-an,DUAN Bo.Analysis of strain localization in overconsolidated clay specimens along different stress paths[J].Rock and Soil Mechanics,2011,32(1):293－298.

[9]蔡正银.砂土的渐进破坏及其数值模拟[J].岩土力学,2008,29(3):580－585.CAI Zheng-yin.Progressive failure of sand and its numerical simulation[J].Rock and Soil Mechanics,2008,29(3):580－585.

[10]陈立文,孙德安.不同应力路径下水土耦合超固结黏土分叉分析[J].岩土力学,2011,32(10):2922－2928.CHEN Li-wen,SUN De-an.Bifurcation analysis of overconsolidated clays with soil-water coupling along different stress paths[J].Rock and Soil Mechanics,2011,32(10):2922－2928.

[11]张洪武,张新伟.基于广义塑性本构模型的饱和多孔介质应变局部化分析[J].岩土工程学报,2000,22(1):23－29.ZHANG Hong-wu,ZHANG Xin-wei.Generalized plastic constitutive model based on strain localization analysis of saturated porous media[J].Chinese Journal of Geotechnical Engineering,2000,22(1):23－29.

[12]MICHALOWSKI R L,SHI L.Deformation patterns of reinforced foundation sand at failure[J].Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2003,129(6):439－449.

[13]HALL S A,BORNERT M,DESRUES J,et al.Discrete and continuum analysis of localised deformation in sand using X-ray μCT and volumetric digital image correlation[J].Geotechnique,2010,60(5):315－322.

[14]宋义敏,马少鹏,杨小彬,等.岩石变形破坏的数字散斑相关方法研究[J].岩石力学与工程学报,2011,30(1):170－175.SONG Yi-min,MA Shao-peng,YANG Xiao-bin,et al.Experimental investigation on failure of rock by digital speckle correlation methods[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(1):170－175.

[15]李元海,靖洪文,朱合华,等.数字照相量测在砂土地基离心试验中的应用[J].岩土工程学报,2006,28(3):306－311.LI Yuan-hai,JING Hong-wen,ZHU He-hua,et al.Experimental investigation on progressive deformation patterns of sand foundation in centrifuge test using digital photogrammetry[J].Chinese Journal of Geotechnical Engineering,2006,28(3):306－311.

[16]王学滨,杜亚志,潘一山.基于DIC 粗-细搜索方法的单轴压缩砂样的应变分布及应变梯度的试验研究[J].岩土工程学报,2012,34(11):2050－2057.WANG Xue-bin,DU Ya-zhi,PAN Yi-shan.Experimental studies of strain distribution and strain gradients for sand specimens in uniaxial compression based on the digital image correlation with coarse-fine search method[J].Chinese Journal of Geotechnical Engineering,2012,34(11):2050－2057.

[17]王学滨,杜亚志,潘一山,等.单向压缩砂土试样应变局部化带测量及影响因素分析[J].西北农林科技大学学报(自然科学版),2012,40(12):191－200.WANG Xue-bin,DU Ya-zhi,PAN Yi-shan,et al.Measurements of strain localization band for sand specimens in uniaxial compression and analysis of its influencing of factors[J].Journal of Northwest A&F University(Natural Science Edition),2012,40(12):191－200.

[18]王学滨,杜亚志,潘一山.单轴压缩湿砂样局部及整体体积应变的数字图像相关方法观测[J].岩土工程学报,2014,36(9):1648－1656.WANG Xue-bin,DU Ya-zhi,PAN Yi-shan.Measurements of local and global volumetric strains for wet sand specimens under uniaxial compression using digital image correlation method[J].Chinese Journal of Geotechnical Engineering,2014,36(9):1648－1656.