水平井多段压裂应力场计算新模型

邓 燕，尹 建, ，郭建春

（1.西南石油大学 油气藏地质及开发工程国家重点实验室，四川 成都 610500；2.中国石油川庆钻探工程有限公司 钻采工程技术研究院，四川 广汉 618300）

1 引 言

水平井多段压裂改造是提高水平井在低渗储层应用效果的技术关键[1－2]，水平井应力场问题是水平井压裂研究的重要问题，影响着压裂过程中裂缝的起裂和延伸。目前对水平井应力场的研究主要考虑井筒内压、压裂液渗流效应以及地应力分量等因素造成的应力变化[3－5]，而水平井多段压裂形成裂缝通常具有先后顺序，先压开的裂缝会在其周围产生诱导应力场，导致井筒周围应力场更为复杂，对人工裂缝形成后产生的诱导应力大小目前主要是使用解析模型进行计算，模型可以计算裂缝高度所在的二维平面上的诱导应力大小，无法计算水平井筒周围水平面上的诱导应力大小，不利于进一步研究受诱导应力干扰下的裂缝延伸过程[6－10]。

本文以均质各向同性的二维平面人工裂缝模型为基础，利用位移不连续理论，推导建立非等裂缝半长、非等间距和任意裂缝倾角的水力裂缝诱导应力场数学模型，结合井筒内压等因素产生的应力变化建立起水平井多段压裂应力场模型。采用应力云图反映了实例井多段压裂压开每条裂缝后水平井筒周围应力分布，并通过每段破裂压力值验证应力场模型的准确性。

2 物理模型

在水平井分段压裂施工作业时，井壁周围岩石的实际受力状态是非常复杂的。如图1 所示，水平井分段压裂井筒内压裂时，井眼内部作用有液柱压力，外部作用有原地应力，岩石内部存在孔隙压力，压裂液由于压差向地层渗滤引起附加压力，射孔等引起应力变化以及已压开裂缝会对井筒周围产生诱导应力影响。

图1 水平井多段压裂井筒示意图Fig.1 Wellbore sketch of horizontal well staged fracturing

由于在复杂应力条件下井壁岩石有可能发生塑性变形，再加上地层不均质性以及各向异性等因素，使得对井筒周围应力场的研究较为困难。因此，为了便于分析，假设岩石是均质各向同性的多孔弹性介质，同时处于线弹性状态，不考虑岩石与压裂液的物理化学作用，同时假设射孔孔眼前端为圆球状，在井筒和射孔孔眼之间有良好连通，井筒和孔眼通道有相同的流体压力，水泥环胶结良好。那么水平井筒周围的应力满足叠加原理，可以通过叠加原理得到在各因素综合作用下的水平井井筒周围诱导应力场分布，定义压应力为正，拉应力为负。水平井筒周围岩石受井筒内压、地应力、压裂液渗流、热应力、射孔和先压开裂缝综合作用下的应力场分布为

3 数学模型

3.1 人工裂缝诱导应力场模型

水平井分段压裂过程中，压开的裂缝将会在其壁面上产生载荷以平衡张开的岩块，同时产生诱导应力场，该问题属于应力边界问题，采用位移不连续法推导建立人工裂缝诱导应力场模型。位移不连续方法是间接边界元法的一种，自1976年由Crouch等[11]建立以来，由于其直接以裂隙面上的相对位移为未知量，在处理不连续体问题时更简单、更方便，因而在岩体工程上受到越来越广泛的应用，对于水平井压裂产生的人工裂缝，裂缝张开后的应力场问题与岩体工程中裂隙边界受外力作用产生相对运动而引起的应力场问题相似，因此，采用位移不连续方法进行研究。

为了研究方便，建立如图2 所示的局部坐标系（s，n）与总坐标系（x，y），水平井筒方向沿x 方向，将人工裂缝离散成N个边界单元，对任意边界单元j，局部坐标系（s，n）与总坐标系（x，y）的倾角为βj，单元j 的位移不连续量记为和和的符号规定为：裂缝的两边相向运动时为正；裂缝的正边相对负边向左运动时为正。

图2 坐标示意图Fig.2 Schematic diagram of coordinate system

3.1.1 应力边界条件

裂缝内部受到均匀的压力 σn=p作用，任意单元j 的已知边界条件可写为

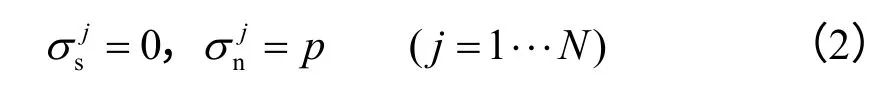
3.1.2 人工裂缝诱导应力场数学模型

单元i 中点的剪应力和法应力可以由j 单元的位移不连续量通过下式得到[11]：

其表达式分别为

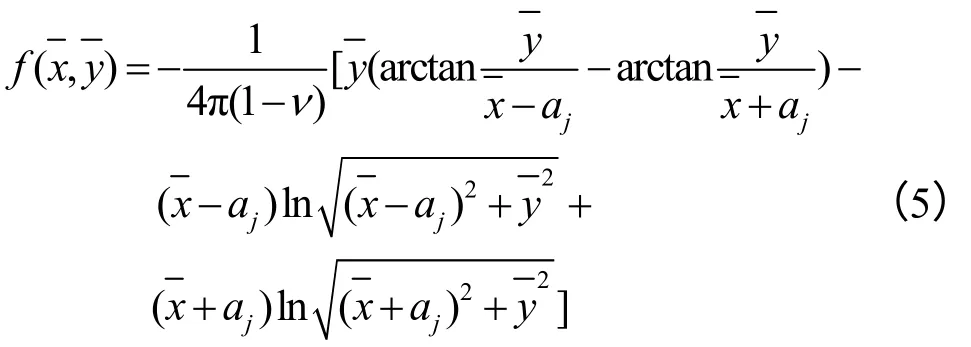
式中： aj为j 单元的半长度(m)。

将式（3）代入到式（2）中可以得到求解人工裂缝诱导应力场数学模型的基本方程组为

该方程组由2N个方程组成，未知量的个数也为2N个，求出各方程中的应力边界影响因素就可以求出各单元的常位移不连续量，再通过计算任意位置的应力边界影响系数就可以确定出该位置的诱导应力值。

3.2 水平井射孔井段井筒周围应力分布模型

将直角坐标系转换为柱坐标系对井筒周围的应力状态进行分析，将水平井井壁视为无限小的变形多孔弹性介质，将水平井井筒和射孔孔眼看成是2个不同尺寸的井眼垂直相交，综合考虑井筒内压、应力场、压裂液渗流条件和温度变化，根据应力叠加原理，得到水平井射孔完井时水平井筒周围任意点i 的应力分布式为[12]

式中：E为弹性模量(MPa)；ν为泊松比；Pw为井筒中压裂液产生的压力(MPa)；c为压力修正系数，无因次；σr(i)、σθ'(i)和 σx(i)分别为i 点处的径向应力、切向应力和轴向应力(MPa)；τrθ(i)、τrx(i)、τθx(i)为i 点处的剪应力分量(MPa)；δ为渗透性系数，无因次；φ为孔隙度，无因次；Pp为孔隙压力(MPa)；αT为水平井井筒周围岩石的线性膨胀系数(1/℃)；ξ为多孔弹性系数，无因次；θ为射孔方位角(°)；θ′为裂缝起裂方位角(°)；R为井筒半径(m)；r为i点距离井筒中心的距离(m)；△T为岩石温差(℃)。

3.2.1 不存在人工裂缝的应力分布模型

未形成人工裂缝前，（x,y,z）坐标系中的正应力和剪应力分量可以通过坐标变换由原地应力得到[12]：

式中：σH、σh、σv分别为最大水平主应力、最小水平主应力和垂直应力(MPa)；α为水平井方位角(°)。

式（7）、（8）构成了不存在人工裂缝条件下的水平井井筒周围应力场的数学模型。

3.2.2 存在人工裂缝的应力分布模型

分段压裂形成人工裂缝后，井筒周围主应力场由原地应力场和人工裂缝产生的诱导应力场组成，见图3。根据叠加原理，分段压裂压开T-1 条裂缝后井筒周围任意一点i的应力为[13－14]

式中：σ′H(i)、σ′h(i)、σ′v(i)为i 点处的复合应力分量(MPa)；σx诱导(i,j)和σy诱导(i,j)为第j 条裂缝对位置i 处产生的诱导应力分量(MPa)。

式（8）中σV、σH和 σh分别由和(i)替换，变换为

式（3）、（7）、（9）和（10）构成了存在人工裂缝条件下的水平井井筒周围应力场的数学模型。

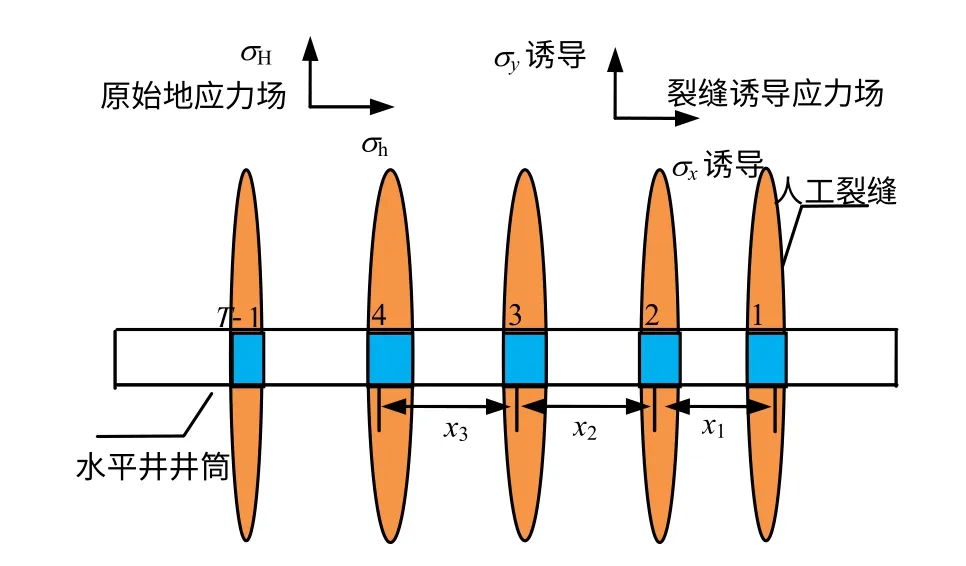
图3 水平井多裂缝应力分布示意图Fig.3 Stress distribution of horizontal well with multiple fractures

3.3 模型求解

对不存在、存在人工裂缝的应力分布模型求解主要区别是在于对人工裂缝诱导应力大小的计算，对于不存在人工裂缝的应力分布模型，应力分量都是解析表达式，代入各参数就可以进行求解；对于存在人工裂缝的应力分布模型，根据前面提到的方法确定了任意位置受到的诱导应力大小后将其代入式（9）计算出复合应力分量，再代入式（10）、（7）得到计算位置的各应力分量。

4 模型的验证与应用

由于应力大小无法监测，因此，不能直接对建立的模型进行验证。由于地层破裂压力大小取决于井壁处的应力分布，而破裂压力值可以监测，因此，使用建立的应力场模型并结合岩石破裂准则预测破裂压力值，通过与实际施工破裂压力值对比，间接验证应力场模型的准确性。地层破裂压力由应力分布模型结合张性破裂准则迭代得到。

采用某油田一口水平井数据进行应力分析以及模型验证，该井对2 831.98～2 834.98 m、2 595.07～2 598.07 m、2 461.98～2 464.98 m 共3 层完成压裂改造，使用PT 软件进行压后净压力拟合，3 段压裂的施工参数及裂缝参数见表1。

应力场及破裂压力计算所用到的地应力参数、储层参数等数据见表2、3。

第1 段压裂前，水平井筒周围应力分量分布见图4(a)～4(c)，从图中可以看出，整个水平井筒周围仅在距离井壁很近的范围应力存在着极小的变化，在距离井壁稍远的位置应力不变。在2 831.98～2 834.98 m 进行压裂后形成一条垂直于水平井筒的

人工裂缝，人工裂缝形成后对水平井筒周围应力场造成了很大影响，与未形成裂缝前相应的应力分量值对比看，人工裂缝形成后在裂缝尖端出现应力集中，造成应力降低，在裂缝周围一定区域造成应力值有较大的升高，人工裂缝造成的应力影响不能被忽略。

表1 施工参数及裂缝参数拟合结果Table 1 Fitting results of construction and fracture parameters

表2 应力场及破裂压力计算基本参数Table 2 Basic calculation parameters of stress field and fracture pressure

表3 储层参数Table 3 Reservoir parameters

图4 不存在裂缝和单条裂缝形成后水平井筒周围应力分布对比Fig.4 Comparison of stress fields around horizontal wellbore between no crack and single crack

对2 595.07～2 598.07 m和2 461.98～2 464.9 m进行压裂后，形成第2 条人工裂缝和第3 条人工裂缝，水平井筒周围应力分布分别见图5、6。从图中可以看出，人工裂缝数量越多，应力之间干扰越严重，水平井筒周围应力分布越复杂。

图5 两条裂缝形成后水平井筒周围应力分布Fig.5 Stress contours around horizontal wellbore for two cracks

图6 3 条裂缝形成后水平井筒周围应力分布Fig.6 Stress contours around horizontal wellbore for three cracks

分别计算未考虑和考虑裂缝诱导应力影响的3条裂缝破裂压力值，将计算结果与压裂施工的实际破裂压力值进行对比，见表4。

第1 段压裂产生的裂缝是初始裂缝，起裂过程中没有受到先压开裂缝的应力干扰，采用不存在人工裂缝的应力分布模型计算结果与实际值误差2.9%；第2 段和第3 段压裂裂缝起裂都会受到之前产生裂缝的应力干扰，采用不存在人工裂缝应力分布模型和采用存在人工裂缝应力分布模型得到的破裂压力值与实际值平均误差分别为5.1%和3.4%。说明建立的井筒周围应力分布模型准确性较高，存在先压开裂缝情况下井筒周围应力分布应该考虑先压开裂缝产生的应力影响。

5 结 论

（1）所建立的水平井多段压裂应力场计算模型不仅考虑了井筒内压、压裂液渗流、地应力、热应力、射孔等因素，还重点考虑了压开人工裂缝产生的诱导应力影响，模型验证表明由于考虑了人工裂缝诱导应力影响，计算结果更准确。

（2）人工裂缝产生后会在其周围产生很大的诱导应力，影响原始地应力，多段压裂压开裂缝条数越多，裂缝间干扰越严重，水平井筒周围应力变化越复杂，后续裂缝的起裂和延伸都将会受到影响，在多段压裂设计中应该对先压裂缝的诱导应力干扰加以考虑。

[1]中国石油勘探与生产公司.水平井压裂酸化改造技术[M].北京:石油工业出版社,2011.

[2]曲占庆,温庆志.水平井压裂技术[M].北京:石油工业出版社,2009.

[3]程远方,王桂华,王瑞和.水平井水力压裂增产技术中的岩石力学问题[J].岩石力学与工程学报,2004,23(14):2463－2466.CHENG Yuan-fang,WANG Gui-hua,WANG Rui-he.Rock mechanics problems in horizontal well fracturing[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(14):2463－2466.

[4]曾凡辉.水平井压裂模拟模型及软件研制[D].成都:西南石油大学,2006.

[5]朱海燕,邓金根,刘书杰,等.定向射孔水力压裂起裂压力的预测模型[J].石油学报,2013,34(3):556－562.ZHU Hai-yan,DENG Jin-gen,LIU Shu-jie,et al.A prediction model for the hydraulic fracture initiation pressure in oriented perforation[J].Acta Petrolei Sinica,2013,34(3):556－562.

[6]曾凡辉,郭建春,刘恒,等.致密砂岩气藏水平井分段压裂优化设计与应用[J].石油学报,2013,34(5):959－968.ZENG Fan-hui,GUO Jian-chun,LIU Heng,et al.Optimization design and application of horizontal wellstaged fracturing in tight gas reservoirs[J].Acta Petrolei Sinica,2013,34(5):959－968.

[7]刘洪,胡永全,赵金洲,等.重复压裂气井诱导应力场模拟研究[J].岩石力学与工程学报,2004,23(23):4022－4027.LIU Hong,HU Yong-quan,ZHAO Jin-zhou,et al.Simulation study of induced stress field in refracturing gas well[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(23):4022－4027.

[8]郭建春,尹建,赵志红.裂缝干扰下页岩储层压裂形成复杂裂缝可行性[J].岩石力学与工程学报,2014,33(8):1589－1596.GUO Jian-chun,YIN Jian,ZHAO Zhi-hong.Feasibility of formation of complex fractures under cracks interference in shale reservoir fracturing[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(8):1589－1596.

[9]尹建,郭建春,赵志红,等.射孔水平井分段压裂破裂点优化方法[J].现代地质,2014,28(6):1307－1314.YIN Jian,GUO Jian-chun,ZHAO Zhi-hong,et al.Fracture rupture point optimization for staged fracturing of perforated horizontal well[J].Geoscience,2014,28(6):1307－1314.

[10]刘立峰,张士诚.通过改变近井地应力场实现页岩储层缝网压裂[J].石油钻采工艺,2011,33(4):71－74.LIU Li-feng,ZHANG Shi-cheng.Net fracturing by changing the surrounding in-situ stress in shale reservoirs[J].Oil Drilling &Production Technology,2011,33(4):71－74.

[11]CROUCH S L.Solution of plane elasticity problems by the displacement discontinuity method[J].International Journal for Numerical Methods in Engineering,1976,10(2):301－343.

[12]HOSSAIN M M,RAHMAN M K,RAHMAN S S.A comprehensive monograph for hydraulic fracture initiation from deviated well bores under arbitrary stress regimes[C]//SPE54360,the 1999 SPE Asia Pacific Oil and Gas Conference and Exhibition.Jakarta,Indonesia:[s.n.],1999.

[13]尹建,郭建春,曾凡辉.水平井分段压裂射孔间距优化方法[J].石油钻探技术,2012,40(5):67－71.YIN Jian,GUO Jian-chun,ZENG Fan-hui.Perforation spacing optimization for staged fracturing of horizontal well[J].Petroleum Drilling Techniques,2012,40(5):67－71.

[14]郭天魁,张士诚,刘卫来,等.页岩储层射孔水平井分段压裂的起裂压力[J].天然气工业,2013,33(12):1－6.GUO Tian-kui,ZHANG Shi-cheng,LIU Wei-lai,et al.Initiation pressure of multi-stage fracking for perforated horizontal wells of shale gas reservoirs[J].Natural Gas Industry,2013,33(12):1－6.