一种结合邻域信息的FCM 图像分割新算法
2015-02-14曾凡玉朱小娟郑金志
曾凡玉,朱小娟,郑金志,龙 颖
(1.重庆师范大学计算机与信息科学学院,重庆 沙坪坝 401331;2.重庆师范大学生命科学学院,重庆 沙坪坝 401331)
图像分割是模式识别和计算机视觉研究的经典课题,是图像分析的热点和难点之一[1-2].Dunn (1974)提出了模糊聚类算法[3],Bezdek(1981)推广了模糊C 均值(FCM)算法[4].由于模糊C 均值将图像分割问题转化为最优化问题,具有坚实的数学理论基础,被广泛应用于图像分割中.但是,FCM 算法对噪声十分敏感.为了增强FCM 算法的鲁棒性,提升算法的抗噪能力,许多学者根据像素与邻域具有高度相关性的图像特性,提出了一系列结合空间邻域信息的改进FCM 算法[5-11].文献[6]将结合空间信息的惩罚项引入FCM 的目标函数,使当前像素的隶属度值大大降低.该算法虽然抑制了噪声的影响,却造成聚类分割后图像边缘的模糊.Wang Ping 等(2008)在文献[10]中将3 ×3 邻域内的隶属度值累加引入空间函数,计算像素点属于第i类的隶属度值,提出了结合空间信息的FCM算法(SFCMp,q).但是,SFCMp,q算法对异常点敏感,并且当遇到强噪声时分割效果不佳.在前人研究的基础上,本文提出结合像素邻域信息、对噪声鲁棒性更强的FCM 图像分割算法.
1 FCM 算法

其中,uik是第k 个样本属于第i 类的隶属度,vi为第i 类的聚类中心,m 为隶属度加权指数(通常取值[1.5,2.5]),dik是第k 个样本到第i 类聚类中心的欧式距离,定义为:
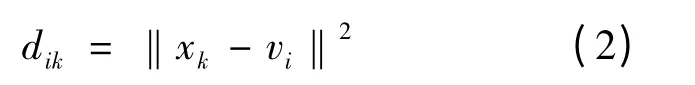
用拉格朗日乘数法求解:

求得隶属度矩阵和聚类中心[4]:

通过对(3)式和(4)式迭代,根据迭代终止条件获得最佳的模糊隶属度矩阵U 和对应的聚类中心矩阵V.最后,按照最大隶属度原则分割图像.
2 FCM 改进算法
2.1 基于空间邻域信息的FCM 算法
定义1 设Ωj表示以xj为中心的N × N 的邻域区间(N 通常取3 或5),ηij是对应的隶属度uij的权重.定义空间函数:

权重ηij为
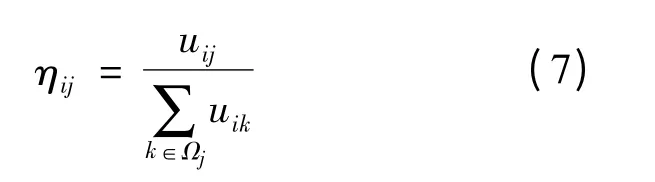
空间函数hij表示像素xj属于第j 类的概率.改进后的隶属度函数为:

新的聚类中心为:

其中:p、q 分别为调节uij、hij的相对重要程度的调节因子.
2.2 上下截集半模糊化处理
保留隶属度矩阵中较模糊的元素,其余元素上下截集,进行半模糊化处理.这样可以提高高隶属度、降低低隶属度对聚类中心的影响,提升算法聚类的准确率.其过程如下[7]:
1)设定上截集阈值tu(0.5 <tu<1.0)、下截集阈值td(0 <td<0.5);
2)当隶属度uij≥tu时,令uij= 1;当uij≤td时,令uij= 0 ;
3)隶属度矩阵中td≤uij≤tu的元素保持不变,继续进行反复迭代划分.
2.3 修正隶属度的硬划分矩阵
图像在获取和传输过程中常常受到噪声的污染使图像质量降低,其中常见的有椒盐噪声和高斯噪声.在图像分割过程中,图像像素的分类最终反映到经过算法迭代后的隶属度矩阵,图像最终依据隶属度的硬划分矩阵H 分割.
1)对于椒盐噪声污染的H.椒盐噪声是在图像上随机分布的黑白相间的亮暗点噪声,可利用中值滤波器有效地滤除椒盐噪声.对H 进行中值滤波,可以有效地对H 进行修正,即:

2)对于高斯噪声污染的H.高斯噪声是指它的概率密度函数服从高斯分布(即正态分布)的一类噪声,对于一幅含高斯噪声的图像,可以进行高斯滤波来改善图像质量.对于硬化分矩阵,同样可以利用高斯滤波器对其进行修正.
二维高斯函数:
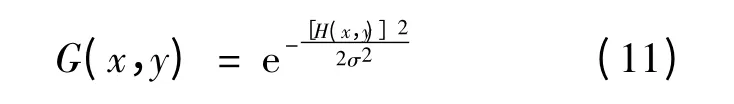
利用高斯函数卷积处理,可以得到修正后的硬化分矩阵:
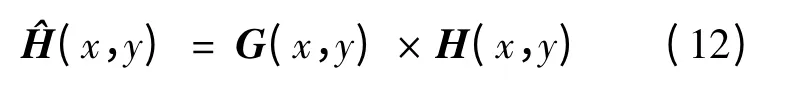
其中,σ 是高斯函数的分布参数,值大小可用于控制对图像的平滑度,σ 取1,(x,y)为修正后的硬划分矩阵,x,y 分别为像素类的行、列所在位置.
2.4 改进算法
综合以上思想,改进算法nSFCMp(new fuzzy C-means with spatial information)具体步骤描述如表1:

表1 改进算法步骤
3 仿真实验
3.1 实验环境及参数设置
联想Z485,AMD A8 - 4500M 1.90GHz,Radeon HD Graphics 32 集成显卡,4G 内存;Windows 7(32bit),Matlab R2010b.
图像分类数c = 6 ,加权指数m = 2 ,ε =1 ×10-5,邻域窗口大小为3×3;上截集阈值tu=0.7,下截集阈值td= 0.3;SFCMp,q中p = {1,2,3},q = 1;nSFCMp中p = {1,2,3}.
3.2 仿真实验分割图像和数据结果
分别采用文献[4]提出的FCM、文献[10]提出的SFCMp,q和本文改进算法nSFCMp对MRI(核磁共振成像)脑图进行仿真实验.
3.2.1 图像分割效果评价指标
1)划分系数Vpc[15]

2)划分熵Vpe[16]

3)Xie-Ben 指数[17]:
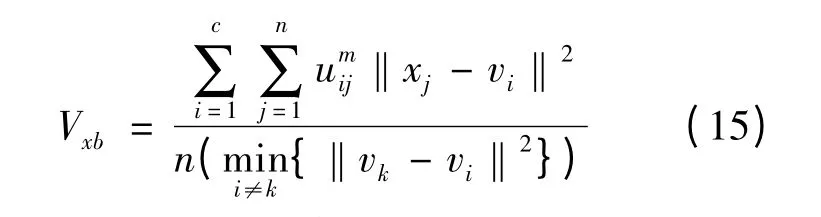
3.2.2 无噪声图像实验
对不含噪声图像图1(a)进行仿真实验,结果如图1(b)~1(d).仿真数据结果如表2所示.
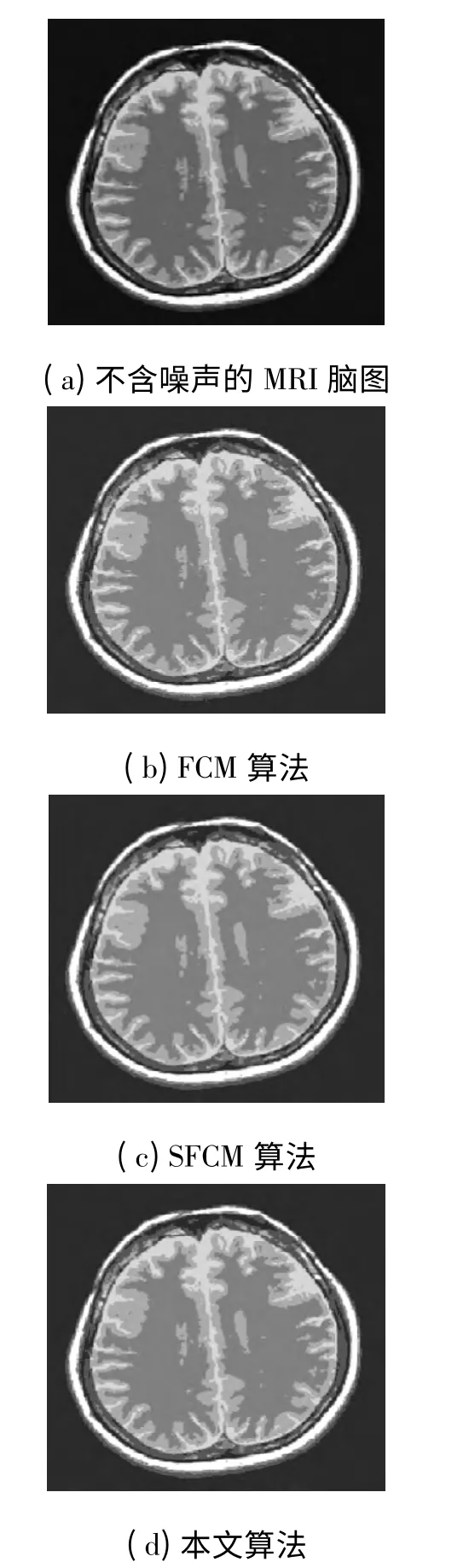
图1 不含噪声的MRI 脑图分割结果对比

表2 不含噪声的MRI 脑图分割对比实验结果
3.2.3 含椒盐噪声图像实验
对含5﹪椒盐噪声的图2(a)进行仿真实验,结果如图2(b)~2(d).仿真数据结果见表3.
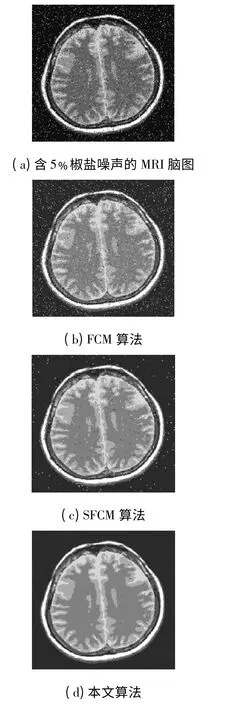
图2 含5﹪椒盐噪声的MRI 脑图分割结果对比

表3 含5﹪椒盐噪声的MRI 脑图分割对比实验结果
3.2.4 含高斯噪声图像实验
对含N(0,0.05)高斯噪声的图3(a)进行仿真实验,结果如图3(b)~3(d).仿真数据结果见表4.

图3 含N(0,0.05)高斯噪声的MRI 脑图分割结果对比

表4 含N(0,0.05)高斯噪声的MRI 脑图分割对比实验结果
3.3 实验结果比较与分析
在MRI 脑图不含噪声的条件下,3 种算法都能取得较好的分割效果.但由表1可以看出:nSFCMp的Vpc值明显大于FCM,Vpe明显小于FCM;nSFCMp的Vpc值大于SFCMp,q,Vpe和Vxb小于SFCMp,q.Vxb度量特征空间内分割结果的类内紧致性程度和类间分离性程度,nSFCMp、SFCMp,q因为考虑了空间邻域信息改变了像素在特征空间中的分布和紧致性,导致Vxb的增加[17].总体上看,nSFCMp算法是一种有效的图像分割算法,分割效果优于SFCMp,q和FCM.
在MRI 脑图含5﹪椒盐噪声的条件下,由于FCM 未考虑空间邻域信息,显然对噪声无能为力;而SFCM 算法考虑了空间邻域信息,对噪声有一定的抑制作用,但分割后的图像仍存在一些噪声.另外,从表3可以看出,nSFCMp的Vpc值明显大于FCM,Vpe明显小于FCM;在p,q 取相同值的条件下,nSFCMp的Vpc值大于SFCMp,q,Vpe和Vxb小于SFCMp,q.同样,nSFCMp、SFCM 因为考虑了空间邻域信息,改变了像素在特征空间中的分布和紧致性,导致Vxb的增加[17].本文算法nSFCMp对椒盐噪声图像进行分割的效果优于另外两种算法.
在MRI 脑图含N(0,0.05)的高斯噪声的条件下,由图3(d)和表4的评价指数对比结果可以看出,nSFCMp能够得到较高的图像分割质量,同时抑制高斯噪声的效果明显优于前两种算法.
4 结论
本文算法通过改进隶属度函数融入像素空间邻域信息,提高了图像的分割质量,同时能够对图像中的噪声进行较好的抑制.采用上下截集半模糊化处理隶属度函数,提高了算法分割的准确率.改进算法只含一个参数,增加了灵活性.新算法在取得较好的分割质量的情况下,对噪声具有很好的鲁棒性.
[1]章毓晋.中国图像工程:2013[J].中国图像图形学报,2014,19(5):649 -658.
[2]李旭超,刘海宽,王飞,等.图像分割中的模糊聚类方法[J].中国图形图像学报,2012,17(4):447 -458.
[3]Dunn J C.A fuzzy relative of the ISODATA process and its use in detecting compact well separated cluster[J].Journal of Cybernetics,1974(3):32 -79.
[4]James C,Bezdek.Pattern recognition with fuzzy objective function algorithms[M].New York:Plenum Press,1981:65 -79.
[5]Krinidis S,Chatzis V.A robust fuzzy local information C- means clustering algorithm[J].IEEE Transaction on Image Processing,2010,19(5):1328 -1337.
[6]Chen S C,Zhang D Q.Robust image segmentation using FCM with spatial constraints based on new kernelinduced distance measure[J].IEEE Transaction on Systems,Man and Cybernetics,PartB:Cybernetics,2004,34 (4):1907 -1916.
[7]路彬彬,贾振红,杨杰,等.基于邻域灰度的模糊C均值图像分割算法[J].光电子·激光,2011,2(3):469 -473.
[8]Zhang D Q,Chen S C.A novel kernelized fuzzy C -means algorithm with application in medical image segmentation[J].Artificial Intelligence In Medicine,2004(32):37 -50.
[9]Li Y L,Shen Y.Fuzzy C -means clustering based on spatial neighborhood information for image segmentation[J].Journal of Systems Engineering and Electronics,2010,21 (2):323 -328.
[10]Wang P,Wang H L.A modified fuzzy C-means algorithm for MRI brain image segmentation.2008 International Seminar on Future BioMedical Information Engineering[C].Wuhan:2008:26 -29.
[11]申铉京,何月,张博,等.基于空间信息及隶属度的FCM 图像分割算法[J].北京工业大学学报,2012,38(7):1073 -1078.
[12]Gong M G,Liang Y,Shi J.Fuzzy C -means clustering with local information and kernel metric for image segmentation[J].IEEE Transaction on Image Processing,2013,22(2):573 -584.
[13]Ji Z X,Liu J Y,Cao G,et al.Robust spatially constrained fuzzy C-means algorithm for brain MR image segmentation[J].Pattern Recognition,2014,47(7):2454 -2466.
[14]李艳灵,沈轶.基于空间邻域信息的FCM 图像分割算法[J].华中科技大学学报:自然科学版,2009,37(6):56 -59.
[15]Bezdek J C.Numerical taxonomy with fuzzy sets[J].Journal of Mathematical Biology,1974(1):57 -71.
[16]Bezdek J C.Cluster validity with fuzzy sets[J].Cybernetics and Systems,1974(3):58 -74.
[17]Xie X L,Lissa,Beni G.A validity measure for fuzzy clustering[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1991,13(8):841 -847.
