对抗性项目技术效益研究

张 辉，刘 炜，户进菊



对抗性项目技术效益研究

张 辉1，刘 炜2，户进菊3

论述了经典技术效益、平衡点及其计算公式，并进一步提出，应根据比赛行为的属性(进攻、防守、控制和相持等)，对技术效益公式中的平衡点进行调整的观点，构建了0.4～0.65之间不同平衡点的技术效益公式。在此基础上，以乒乓球项目为例，以比赛行为(一三拍、二四拍和四拍以后)的平均得分率作为选取不同平衡点技术效益计算公式的依据，分别计算它们各自的技术效益值。结果发现，采用不同平衡点技术效益所计算的各项比赛行为的技术效益值在P70，P50和P30都十分接近。这样可以简化技术效益评估模型与各项比赛行为之间的比较。同时，通过个案和综合分析案例，表明技术效益评估在训练、比赛实践中应用的可行性。

技术效益；评估模型；平衡点；乒乓球

在对抗性项目的技、战术分析中，最常用的两项指标是得分率和使用率。其中，得分率反映的是一项比赛行为(包括技术或战术)的质，而使用率则反映一项比赛行为的量。在以往绝大多数的相关研究中，都是通过得分率和使用率两项指标分别来对运动员的比赛行为特征进行分析[1，2，4，5-7]。

但在实际应用过程中，常常会碰到得分率和使用率不一致的情况，例如，一项比赛行为的得分率是0.7，使用率为0.3；而另一项比赛行为的得分率为0.6，使用率为0.4，人们就很难判断这两项比赛行为的使用效果或对比赛取胜的贡献度，也很难简单地用相乘或其他计算方法来确认。鉴此，张辉和刘炜等人(2013)根据得分率与使用率之间的关系特征，首次提出了技术效益的概念，以便能够定量地对运动员比赛行为的效果做出分析与评估[3，8]。

然而，在进一步的研究中发现，运动员的比赛行为具有不同的属性，例如，进攻、防守、控制、相持等等，不同的比赛行为，其得分的难易程度不同，或者不同比赛行为的得分对于比赛获胜有着不同的意义。因此，本研究提出应根据不同属性的比赛行为，对技术效益计算公式作进一步的改进。

1 经典技术效益、平衡点与计算公式

1.1 技术效益

技术效益是指运动员比赛行为(技术或战术)的使用效率，它受到得分率与使用率两个指标的影响。当比赛行为得分率大于0.5的时候，比赛行为的使用率越大，对比赛获胜产生的积极影响也就越大，即技术效益为使用率的递增函数；当比赛行为得分率小于0.5时，其使用率越大，对比赛获胜产生的消极影响也就越大，即技术效益是使用率的递减函数；当比赛行为的得分率等于0.5时，无论使用率如何，比赛双方所获得的益处相等，即技术效益始终等于0.5(图1)。为了与后续演进后的技术效益计算方法相区别，在此称其为经典技术效益。

图1 本研究比赛行为得分率、使用率与技术效益关系示意图

1.2 平衡点

依据经典技术效益的概念，当运动员某个比赛行为的得分率，既不会随着比赛行为使用率的增加，而使得技术效益提高(或降低)，也不会随着使用率的降低，而使得技术效益降低(或提高)，此得分率称之为平衡点。理论上来说，经典技术效益计算公式中的平衡点应该是0.5，即a=0.5。

1.3 经典技术效益计算方法

按照上述技术效益与平衡点(a=0.5)的性质，技术效益的计算公式如下：

记x为得分率，0≤x≤1；y为使用率，0≤y≤1；TE为技术效益函数。首先设计一个函数TE1，使其满足技术效益的3个主要性质：1)当得分率x>α时，使用率越高，技术效益值也越高；2)当得分率x<α时，使用率越高，技术效益则越低；3)当得分率x=α=0.5时，无论使用率y如何，TE1的值不变。

TE1=(1+y)x-0.5

(1)

然后用TE1的二次函数拟合TE1与TE的3对数据，得到技术效益函数TE的表达式：

(2)

公式(2)TE值满足下列属性：1)TE总体满足：0≤TE≤1，TE值越大，说明该项技术效益越高；2)x=1且y=1时，表明该项技术的效益达到了最大化，即TE值为1；3)x=0.5时，无论使用率如何，即TE值都取0.5；4)x=0且y=1时，表明该项技术的效益最小，即TE值为0。

因此，根据本研究对经典技术效益的定义，运动员所有涉及到得分率和使用率的各种比赛行为，无论是技术行为，还是战术行为等，都适合用技术效益公式对其进行分析与评估。

2 技术效益计算方法的演进

2.1 比赛行为属性与平衡点

然而，在比赛分析实践过程中，由于运动员各种比赛行为的属性不同，如有进攻行为、防守行为、控制行为以及相持行为等，它们在比赛中所起的作用不同，得分难易程度差别也很大。例如，当一项防守型或控制型技术行为的得分率达到0.4以上，实际上该项技术会对比赛获胜起到非常有益的作用；相反，如果一项强进攻技术行为的得分率仅仅只超过0.5，那么，它将会对比赛的取胜带来较大的负面效应。

因此，经典技术效益计算公式中的理论平衡点(a=0.5)，在实际应用过程中，需要依据比赛行为的属性对其进行调整，这样才能更好地对各项比赛行为的效益做出分析、比较与评估。

2.2 基于不同平衡点的技术效益计算公式

公式(3～8)是基于不同平衡点的技术效益算法。例如，公式(3)的平衡点为0.4，即当得分率等于0.4时(即a1=0.4)，无任使用率如何，其技术效益值始终保持为0.5；而当得分率大于0.4时(即a1>0.4)，技术效益即为使用率的递增函数；当得分率小于0.4时(即a1<0.4)，技术效益才是使用率的递减函数。

同理，公式(4)～(8)是平衡点分别取0.45～0.65时的技术效益计算公式，它们具有与公式(3)的同样功能。由于精确值公式比较复杂，本研究给出的各项系数值保留6位有效数字，其精度能够满足实际使用要求。

当平衡点为0.4时，技术效益计算公式如公式(3)：

TE=-2.66029+4.60565×[(1+y)x-0.40]-1.44536×[(1+y)2(x-0.40)]

(3)

当得分率平衡点为0.45时，技术效益计算公式如公式(4)：

TE=-2.15455+3.73179×[(1+y)x-0.45]-1.07724×[(1+y)2(x-0.45)]

(4)

当得分率平衡点为0.5时，技术效益计算公式如公式(5)：

TE=-1.70711+2.91421×[(1+y)x-0.50]-0.707107×[(1+y)2(x-0.50)]

(5)

当得分率平衡点为0.55时，技术效益计算公式如公式(6)：

TE=-1.28880+2.09834×[(1+y)x-0.55] -0.309533×[(1+y)2(x-0.55)]

(6)

当得分率平衡点为0.6时，技术效益计算公式如公式(7)：

TE=-0.874143+1.22957×[(1+y)x-0.60]+0.144572×[(1+y)2(x-0.60)]

(7)

当得分率平衡点为0.65时，技术效益计算公式如公式(8)：

TE=-0.435858+0.241319×[(1+y)x-0.65]+0.694540×[(1+y)2(x-0.65)]

(8)

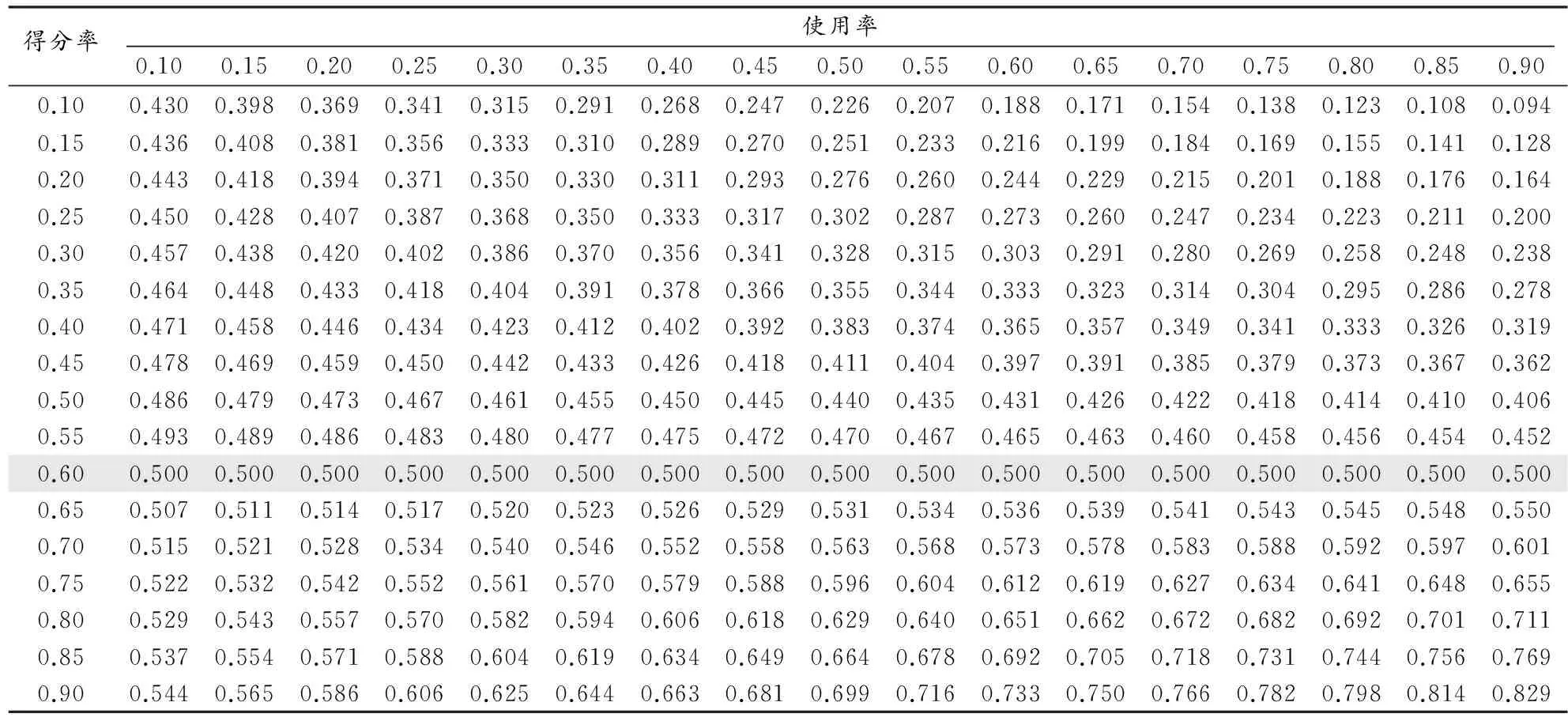
上述(3)～(8)这组公式的推导过程非常复杂，但其原理与经典技术效益公式相同，该组公式的合理性可以通过数值计算进行验证。如平衡点为0.6时，得分率和使用率各种组合下的技术效益值如表1所示，表中的灰色带即为平衡点。

表1 本研究得分率和使用率各种组合下的技术效益值一览表(平衡点为0.6)

Table 1 Technique Effectiveness Value under Difference Combination of Scoring Rate and Usage Rate(Balance Point 0.6)

得分率使用率0.100.150.200.250.300.350.400.450.500.550.600.650.700.750.800.850.900.100.4300.3980.3690.3410.3150.2910.2680.2470.2260.2070.1880.1710.1540.1380.1230.1080.0940.150.4360.4080.3810.3560.3330.3100.2890.2700.2510.2330.2160.1990.1840.1690.1550.1410.1280.200.4430.4180.3940.3710.3500.3300.3110.2930.2760.2600.2440.2290.2150.2010.1880.1760.1640.250.4500.4280.4070.3870.3680.3500.3330.3170.3020.2870.2730.2600.2470.2340.2230.2110.2000.300.4570.4380.4200.4020.3860.3700.3560.3410.3280.3150.3030.2910.2800.2690.2580.2480.2380.350.4640.4480.4330.4180.4040.3910.3780.3660.3550.3440.3330.3230.3140.3040.2950.2860.2780.400.4710.4580.4460.4340.4230.4120.4020.3920.3830.3740.3650.3570.3490.3410.3330.3260.3190.450.4780.4690.4590.4500.4420.4330.4260.4180.4110.4040.3970.3910.3850.3790.3730.3670.3620.500.4860.4790.4730.4670.4610.4550.4500.4450.4400.4350.4310.4260.4220.4180.4140.4100.4060.550.4930.4890.4860.4830.4800.4770.4750.4720.4700.4670.4650.4630.4600.4580.4560.4540.4520.600.5000.5000.5000.5000.5000.5000.5000.5000.5000.5000.5000.5000.5000.5000.5000.5000.5000.650.5070.5110.5140.5170.5200.5230.5260.5290.5310.5340.5360.5390.5410.5430.5450.5480.5500.700.5150.5210.5280.5340.5400.5460.5520.5580.5630.5680.5730.5780.5830.5880.5920.5970.6010.750.5220.5320.5420.5520.5610.5700.5790.5880.5960.6040.6120.6190.6270.6340.6410.6480.6550.800.5290.5430.5570.5700.5820.5940.6060.6180.6290.6400.6510.6620.6720.6820.6920.7010.7110.850.5370.5540.5710.5880.6040.6190.6340.6490.6640.6780.6920.7050.7180.7310.7440.7560.7690.900.5440.5650.5860.6060.6250.6440.6630.6810.6990.7160.7330.7500.7660.7820.7980.8140.829

为了能更形象地说明平衡点在技术效益计算公式中的作用与意义，分别选取了得分率等于0.55、0.60、0.65、0.70(图2(1)、2(2)、2(3)、2(4)的左半部分)和得分率为0.45、0.40、0.35、0.30(图2(1)、2(2)、2(3)、2(4)右半部分。选取使用率为0.1～1，将其分别代入6个不同平衡点的技术效益计算公式，即平衡点分别为0.40，0.45，0.50，0.55，0.60和0.65。

从图2可以看出，基于不同平衡点的技术效益算法与经典技术效益算法主要差异有以下3个方面：

1.当同一个得分率代入不同平衡点的技术效益公式中进行计算，会获得不同的技术效益值。

2.同一个得分率，代入平衡点越低的技术效益公式，其技术效益值越大。这是因为平衡点越低的比赛行为，其在比赛中的得分难度就越大，如果得分率相同，那么，平衡点越低的比赛行为，其技术效益值就会越高。从图2中可以看出，平衡点为0.4的公式所计算的技术效益值最大，依次分别为0.45，0.50，0.55，0.60，最小值是平衡点为0.65的公式所计算的值。

3.当一个大于0.5的得分率(如0.55或0.60)，代入平衡点为0.65的技术效益计算公式，其效益值随使用率的增加而下降，并始终小于0.5[图2(1)]；当一个小于0.5的得分率(如0.45)，代入平衡点为0.40的技术效益计算公式，其效益值随使用率的增加而增加，并始终大于0.5[图2(2)]。

3 技术效益公式的实际应用

3.1 经典技术效益公式的应用

经典技术效益公式即平衡点取0.5的计算方法。以乒乓球项目为例，张辉和刘炜等(2013)运用经典技术效益公式，对121场优秀男子和123场优秀女子乒乓球比赛进行了计算，并采用百分位数(P70、P50和P30)的方法建立了技术效益评估标准(表2)。

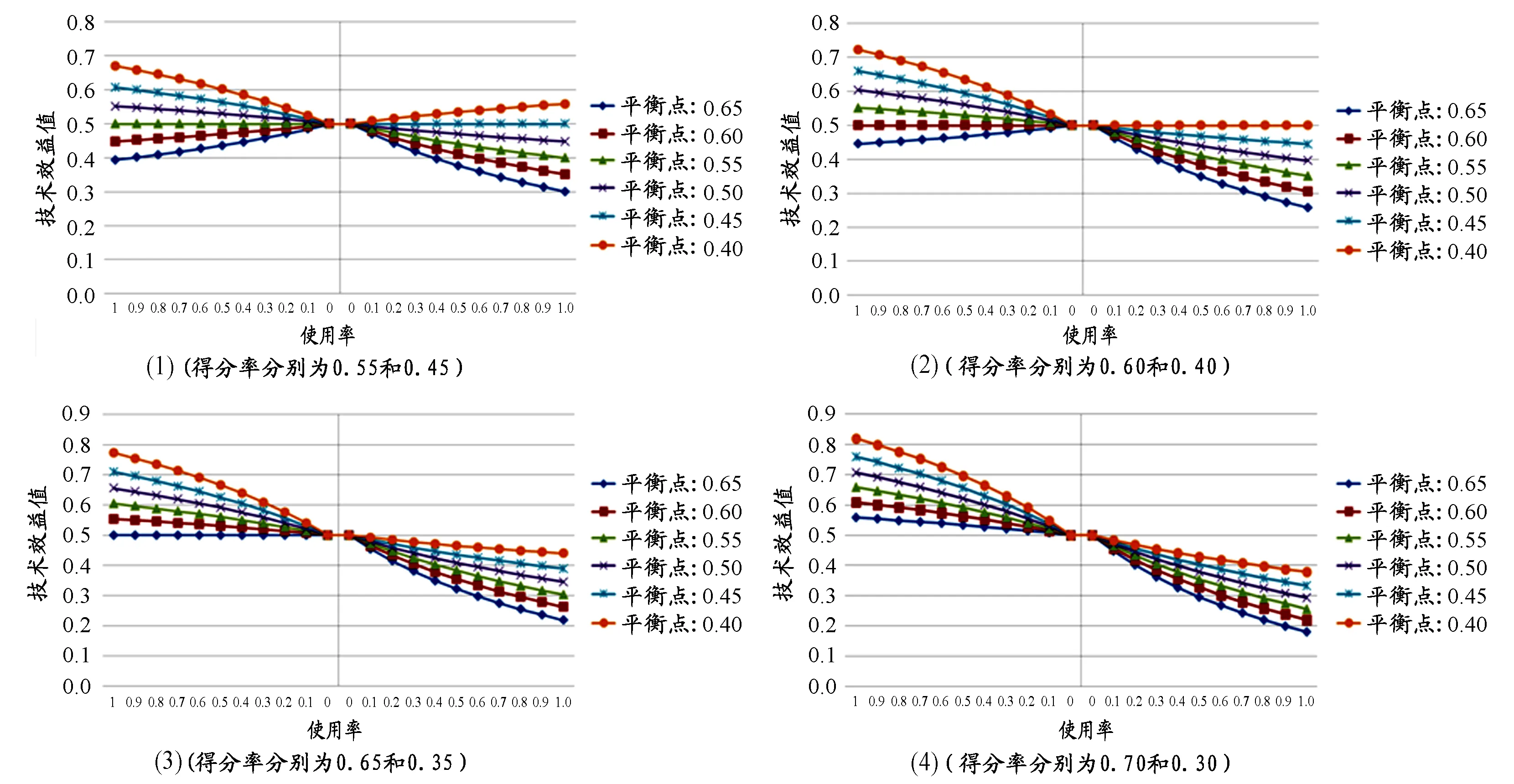
图2 本研究基于不同平衡点计算公式的技术效益值曲线图(得分率取0.3～0.7)

表2 本研究优秀乒乓球运动员经典技术效益评估标准一览表(张辉和刘炜等，2013)

注：TE1,3为乒乓球比赛一三拍的技术效益值；TE2,4为二四拍的技术效益值；TE>4为四拍以后的技术效益值。

图3和图4是运用经典技术效益评估标准对中、外优秀运动员进行的比较。从总体上看，中国运动员无论是男子还是女子，在一三拍、二四拍和四拍以后的技术效益值均要高于外国运动员。例如，在男子方面，中国运动员在一三拍的技术效益值为0.554(良好)，外国运动员为0.530(合格)，两者有非常显著的差异(t=3.115,P<0.01)；在二四拍上，中国运动员的技术效益值为0.521(良好)，外国运动员为0.485(合格)，有非常显著的差异(t=4.388,P<0.01)；中国运动员四拍以后的技术效益也要明显好于外国运动员，其TE为0.473(优秀)，外国运动员TE值仅为0.426(合格)，具有非常显著的差异(t=5.142,P<0.01)[8](图3)。

在女子方面，中国运动员的一三拍技术效益值为0.563(优秀)，外国运动员为0.537，两者具有非常显著性差异(t=3.864,P<0.01)；中国运动员二四拍的技术效益值为0.508(良好)，外国运动员为0.478(合格)，两者具有非常显著性差异(t=3.485,P<0.01)；中国运动员四拍以后的技术效益值为0.484(优秀)，外国运动员为0.435(合格)，两者具有非常显著性差异(t=4.098,P<0.01[8]，图4)。

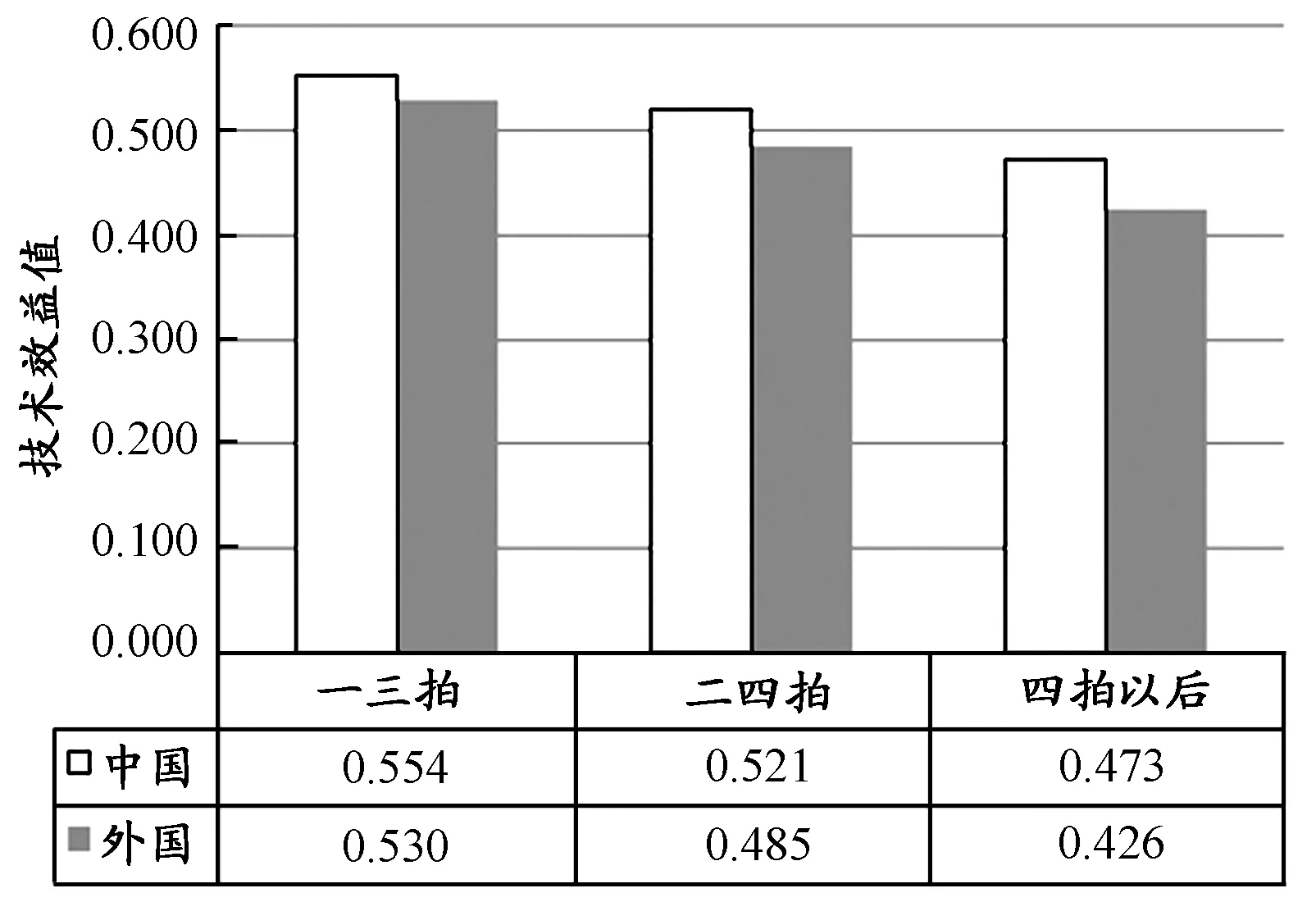
图3 本研究中国与外国男子运动员各项技术指标的技术效益值对比示意图

3.2 演进后的技术效益公式应用

3.2.1 选取平衡点

由于各种比赛行为的属性差异，应选用不同平衡点的技术效益计算公式。平衡点的确定可参考该项比赛行为的平均得分率，究其原因：1)平均得分率可以代表该比赛行为的平均水平；2)理论上说，当运动员某个比赛行为的得分率大于平均水平，表明该比赛行为对比赛获胜具有积极性的影响；3)同样，当运动员某个比赛行为的得分率小于平均水平，则表明它对比赛获胜起消极性的影响。

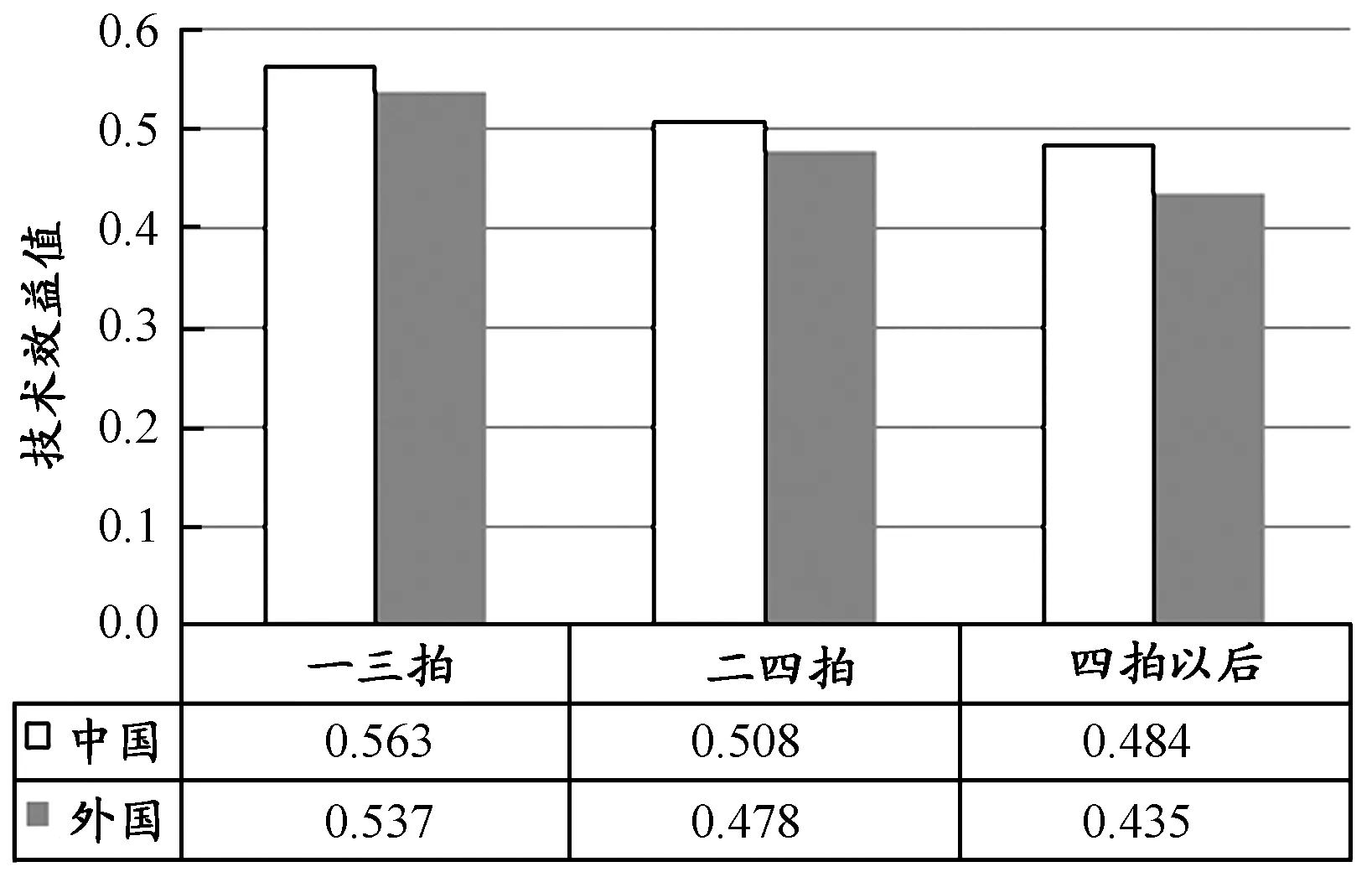
图4 本研究中国与外国女子运动员各项技术指标的技术效益值对比示意图

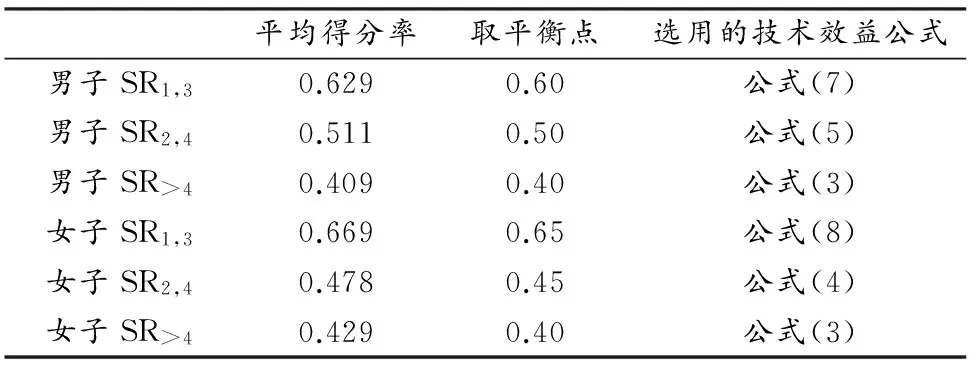
表3是应用上述比赛(表2)同样的原始观察数据，计算121场优秀男子和123场优秀女子乒乓球比赛各项技术行为的平均得分率，并选取略低于平均得分率一档的平衡点作为技术效益计算公式。例如，男子一三拍平均得分率(SR1,3)为0.629，则选取技术效益公式(7)，即平衡点为0.6时的技术效益公式(表3)。

表3 本研究基于不同平衡点选取的乒乓球比赛技术效益公式一览表

Table 3 Selection of Technique Effectiveness Formula based on Different Balance Points in Table Tennis

平均得分率取平衡点选用的技术效益公式男子SR1,30.6290.60公式(7)男子SR2,40.5110.50公式(5)男子SR>40.4090.40公式(3)女子SR1,30.6690.65公式(8)女子SR2,40.4780.45公式(4)女子SR>40.4290.40公式(3)

注：SR1,3为乒乓球比赛一三拍的得分率；SR2,4为二四拍的得分率；SR>4为四拍以后得分率。

3.2.2 确定新的技术效益评估标准

依据表3中各项比赛行为所选用的技术效益公式，重新计算121场优秀男子和123场优秀女子乒乓球比赛各项比赛行为的技术效益值，并运用百分位的方法对其进行分级。

从表4中可以看到，以乒乓球比赛各项比赛行为的平均得分率为参考，选用不同平衡点的技术效益公式计算后，无论是男子还是女子，他们各项比赛行为的技术效益值在P70、P50和P30，都非常的接近(标准差分别为0.007、0.005和0.008)。因此，可以取男子和女子的各项比赛行为技术效益值在P70、P50和P30的平均值作为评估的分级标准，从而简化了各项比赛行为技术效益的评估与分析方法，而不用考虑各项比赛行为所存在的技术属性与性别方面的差异。

表4 本研究各项技、战术指标的技术效益百分位值一览表

Table 4 Percentile Value of Technique Effectiveness of Each Technique and Tactic Index

P70P50P30男子TE1,30.5300.5100.486男子TE2,40.5330.5060.477男子TE>40.5380.5080.469女子TE1,30.5290.5060.487女子TE2,40.5350.5130.482女子TE>40.5480.5180.490X0.5360.5100.482SD0.0070.0050.008

鉴此，本文在下列案例研究中，无论是男子运动员，还是女子运动员以及各项比赛行为之间，均采用下列技术效益评估标准：TE≥0.536为优秀；0.536>TE≥0.510为良好；0.510>TE≥0.482为合格；TE<0.482为不合格。

3.2.3 案例分析

3.2.3.1 技术效益个案分析(运动员A技术效益)

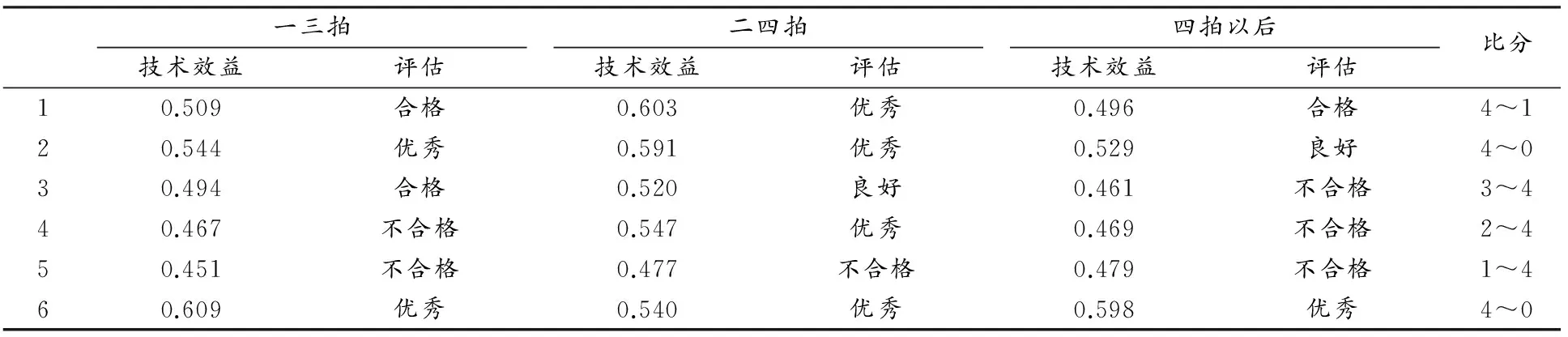
表5是奥运会乒乓球冠军运动员A在2010-2012年国际比赛的技术效益评估。从中可以看到，他的二四拍的技术效益值最高，为0.534(良好水平)，其次是一三拍技术，其技术效益值为0.518(良好水平)，而他的四拍以后技术效益最低，为0.500(合格水平)。此外还发现，尽管运动员A的一三拍和二四拍的总体水平达到了良好，但在某些场次比赛中技术效益值较低，起伏较大，还出现不合格的现象，表明运动员A的技术发挥稳定性不够。

表5 本研究运动员A在2010—2012年国际比赛中技术效益值与评估一览表

Table 5 Athlete A Technique Effectiveness Values and Valuations in the International Competition during 2010-2012

一三拍二四拍四拍以后比分技术效益评估技术效益评估技术效益评估10.509合格0.603优秀0.496合格4～120.544优秀0.591优秀0.529良好4～030.494合格0.520良好0.461不合格3～440.467不合格0.547优秀0.469不合格2～450.451不合格0.477不合格0.479不合格1～460.609优秀0.540优秀0.598优秀4～0

续表 5

3.2.3.2 技术效益综合分析

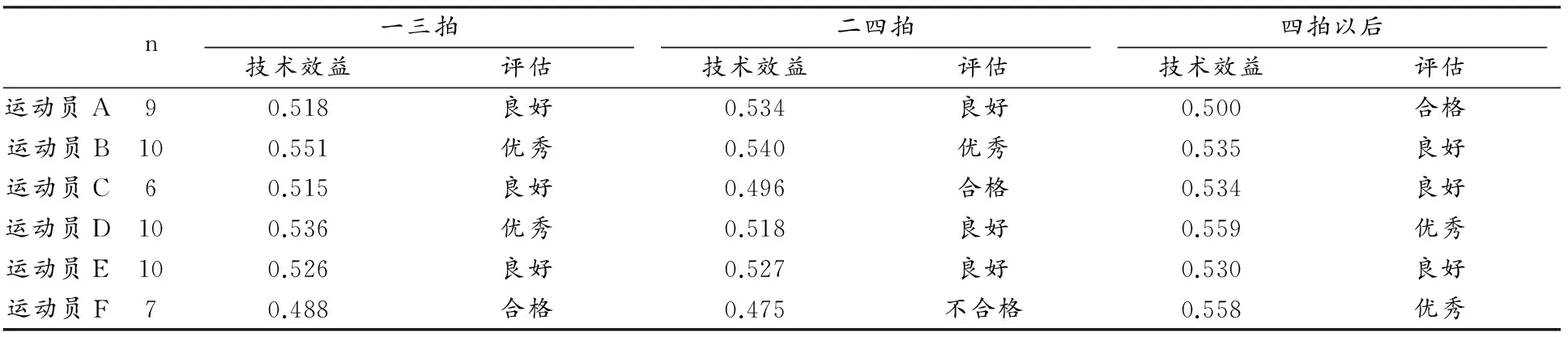
随机选取了3名男子世界冠军(运动员A、运动员B、运动员C)和3名女子世界冠军(运动员E、运动员D、运动员F)2010-2012年期间与世界一流选手之间的比赛进行分析(表6)。可以看出，男子运动员B的比赛行为技术效益最好，其中一三拍技术效益列所有运动员之首；女子运动员D的技术效益最好，其四拍以后的技术效益尤其突出。运动员C的二四拍技术效益较低，而运动员F的一三拍和二四拍的技术效益较差，但其四拍以后的技术效益还是非常高的。

表6 本研究我国6名优秀运动员2010-2012年国际比赛技术效益值与评估一览表

Table 6 Six Chinese Elite Player’s Technique Effectiveness Values and Valuations in the International Competition during 2010-2012

n一三拍二四拍四拍以后技术效益评估技术效益评估技术效益评估运动员A90.518良好0.534良好0.500合格运动员B100.551优秀0.540优秀0.535良好运动员C60.515良好0.496合格0.534良好运动员D100.536优秀0.518良好0.559优秀运动员E100.526良好0.527良好0.530良好运动员F70.488合格0.475不合格0.558优秀

4 讨论

在本研究中，提出应根据比赛行为不同的属性(进攻、防守、控制)运用不同平衡点的技术效益计算公式，能够更加精确地反映运动员各项技术的使用效率。例如，当一项进攻性战术行为与一项防守型战术行为的得分率和使用率相同时，由于它们的属性不同。因此，所选用的技术效益公式也应该不同，那么，防守型战术行为的技术效益自然就高于进攻性战术行为，这样的评估结果更符合竞技体育比赛的客观规律，即当得分率和使用率相等的时候，越不容易得分的技术或战术行为(即平衡点越低)，其技术效益值就越大。

在实际应用过程中，可以参考某项比赛行为(技术或战术)的平均得分率，作为选取技术效益公式平衡点依据。例如，在乒乓球比赛中，以优秀运动员一三拍、二四拍和四拍以后技术的平均得分率作为选取技术效益公式平衡点的依据。然后，使用不同平衡点的技术效益计算公式，其结果是各项比赛行为的技术效益值非常接近，这样不但可以简化评估模型，而且，有利于各项比赛行为之间进行比较。

5 结论

经典技术效益公式诠释竞技体育中得分率与使用率的关系特征，演进后的基于平衡点的技术效益公式更加精确地反映各项比赛行为的实际效益。在实际操作过程中，可参考得分率平均值，作为技术效益公式平衡点的依据，从而可以简化技术效益的评估与分析方法。

[1]戴金彪，管颖，卢志泉，等.“21分制”对羽毛球男单技战术发展的影响[J].上海体育学院学报，2008，28(2)：86-89.

[2]侯会生，张磊，夏辉，等.足球比赛核心制胜技战术指标的探讨分析[J].北京体育大学学报，2013,36(5)：134-139.

[3]黄文文，张辉，刘炜.乒乓球奥运冠军张继科技术使用效能的评估[J].中国体育科技， 2014，50(3)：31-34.

[4]孟范生，曾倩，张涛，等.排球进攻战术水平的诊断与评定[J].上海体育学院学报，2002，26(2)：58-62.

[5]吴焕群.第40届世界乒乓球锦标赛观察报告[J].中国体育科技，1989，25(8)：21-29.

[6]赵传杰，张辉.击剑比赛技战术分析理论与实践[M].北京：人民体育出版社，2010.

[7]张辉.球类比赛计算机诊断与分析[M].哈尔滨：黑龙江科技出版社，2006.

[8]ZHANG H,LIU W,HU J,etal.Evaluation of elite table tennis players’ technique effectiveness[J].J Sports Sci,2013,31(14):1526-1534.

Study on Technique Effectiveness of Antagonistic Sports Event

ZHANG Hui1,LIU Wei2,HU Jin-ju3

This paper discusses classic technique effectiveness,balance point and formula,and further proposes that the balance points of the technique effectiveness formula should be adjusted according to the attributes of athletes’ game actions (offense,defense,control and stalemate,etc.) and constructs technique effectiveness formulas for the different balancing points between 0.4 and 0.65.On this basis,taking table tennis as example,this paper chooses the average scoring rate of each game action (the first/third stroke,second/fourth stroke and after the fourth stroke) of elite players as the foundation for determining the technique effectiveness evaluation formula and calculates the value of their respective technical effectiveness.The findings show that the technique effectiveness values of different game actions are very close at P70,P50and P30.In this way,the evaluation model and the comparison between various kinds of game action are simplified.At the same time,the individual and comprehensive case analysis shows that it is feasible to apply the technique effectiveness evaluation to training and competition practice.

techniqueeffectiveness;evaluationmodel;balancepoint;tabletennis

2014-08-19；

2015-08-10

国家体育总局国家队科研综合攻关研究课题 (2011A081)。

张辉(1964-)，男，浙江宁波人，教授，博士，博士研究生导师，主要研究方向为运动技、战术分析，Tel：(0571)88273624，E-mail：zhang_hui@zju.edu.cn；刘炜(1963-)，男，上海人，副教授、硕士研究生导师，主要研究方向为体育统计学，Tel：(021)51253049，E-mail：lw@sus.edu.cn；户进菊(1966-)，女，河南新乡人，副教授、博士， 主要研究方向为体育科技英语，Tel：(021)51253094，E-mail：hjjlisa@163.com。

1.浙江大学 教育学院 体育学系，浙江 杭州 310028；2.上海体育学院 信息技术中心，上海 200438；3.上海体育学院 体育新闻传播与外语学院，上海 200438 1.Zhejiang University,Hangzhou 310028,China；2.Shanghai University of Sport,Shanghai 200438,China；3.Shanghai University of Sport,Shanghai 200438,China.

1000-677X(2015)09-0044-06

10.16469/j.css.201508000

G846

A