城市路网交叉口信号预测及配时控制＊

张 骥，汤元会

（1．西安工程大学 电子信息学院，西安710048；2．陕西省计量科学研究院 电磁计量中心，西安710065）

交叉口信号控制是城市交通管理的重要手段，合理的信号配时对交通流在路网中的高效平稳运行至关重要．随着城市路网规模的不断扩大和交通流量的日益增长，单个交叉口的信号优化或干线的协调控制均难以达到理想的控制效果．因此，必须从整个路网出发进行交叉口信号的协调优化．

针对多交叉口的协调控制问题，国内外学者提出了很多方法，包括模糊控制［1］、最优控制［2］、混合Petri网［3］及模型预测控制［4-5］等．其中，模型预测控制方法由于具有模型预测、滚动优化和反馈校正的特点，并能方便处理被控变量和决策变量的各种约束受到了广泛关注．在交通领域中，模型预测控制已经在高速公路网络和城市交通网络控制中得到了应用［6］．文献［7］提出了一个高速公路和城市交通网络的混合交通流模型，并采用模型预测控制方法对匝道口和交叉口信号进行协调控制；文献［8］根据路段车辆数动态变化关系提出了一个同时适用于欠饱和、饱和和过饱和3种交通状况的宏观交通流模型，但该模型将仿真时间步长设置为1s，使模型的计算复杂度大幅增加．为了减小模型预测控制器的在线计算量，文献［9］将仿真时间步长设置为交叉口的信号周期，极大地减小了模型的计算复杂度，提高了控制器的在线计算速度．然而，上述交通流模型在计算车辆的路段延误时均假设车辆按照自由速度行驶．在现实中，由于车辆在路段中行驶的速度受车辆密度限制，即驾驶员为了保证行车安全会根据不同的车辆密度调整车辆的行驶速度．本文在考虑车辆行驶时速度与密度关系的基础上，提出了描述交通流动态关系的排队模型，并以该模型作为预测模型，设计了相应的模型预测控制器用于交叉口的协调控制．为克服传统的以总旅行时间最短为性能指标的控制方式所带来的部分路段长时间拥堵问题［9］，文中基于路网排队状态均衡的交叉口协调控制思想，根据路网中各个路段上的车辆排队长度对交叉口各相位的绿灯时间进行实时动态调整，从而避免部分路段因绿灯时间分配不足导致的长时间拥堵．

1 排队模型

在文献［9］的基础上，以路段为基本单元，从交通流经交叉口驶入路段并行至队尾、交通流排队及交通流驶离路段的全过程建立描述路网中交通流动态关系的宏观模型，如图1所示．

交通流的消散率是根据路段的饱和程度不同分别由排队车辆及到达车流率、路段的饱和流率及绿灯时长和下游路段的空闲容积率共同决定，即

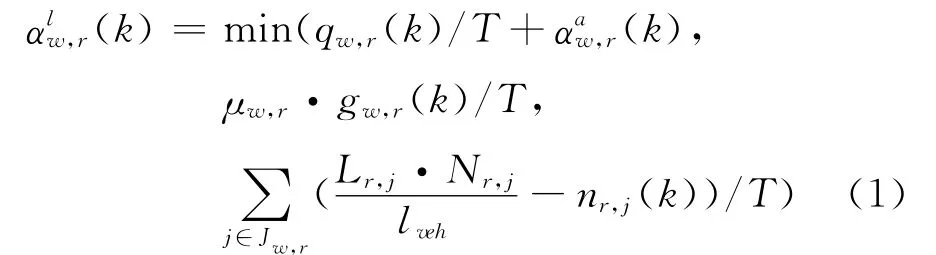
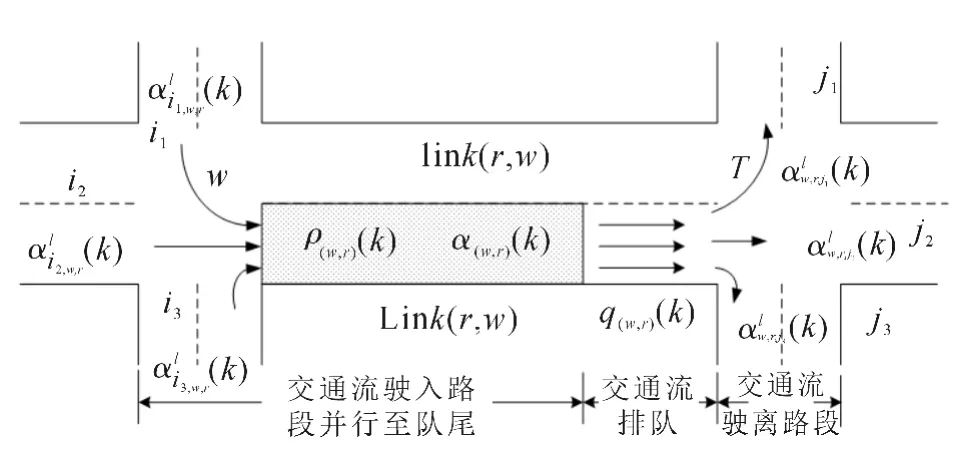
图1 路段交通流运行示意图Fig．1 Diagram of road traffic flow

驶入下游不同路段的车流率取决于驶离路段的车流率及相应路段的转向率，即

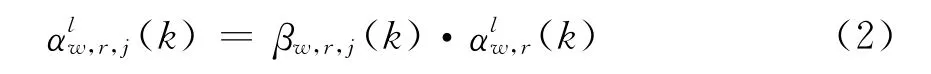
车辆到达率是由驶离上游不同路段的车流率经一定的时间延误后到达队尾构成，即

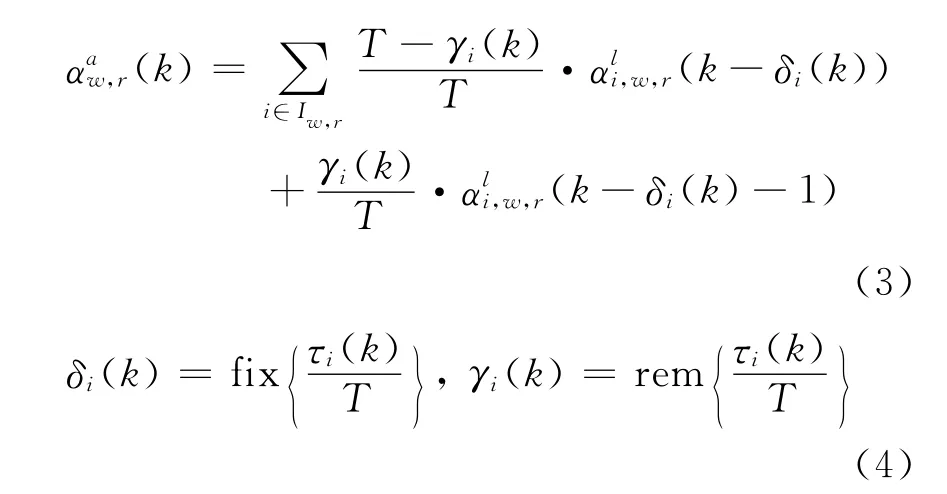
式中：fix（x）表示小于或等于x的最大整数；rem（x）表示x的小数部分；τi（k），i∈Iw，r分别为上游不同路段驶入车流率的延误时间．

不同转向的车流驶入路段后将驶过相同的距离到达队尾，因此不同转向车流的路段延误相同，即

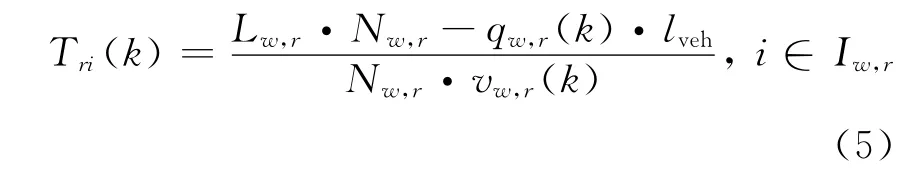
式中：vw，r（k）为第k个采样周期路段（w，r）上车辆行驶的平均速度；Nw，r为路段（w，r）的车道数；Lw，r为路段（w，r）的长度．其中，当路段的车流密度小于路段的最小密度，或大于最大密度时，车流的速度由式（6）计算［10］为

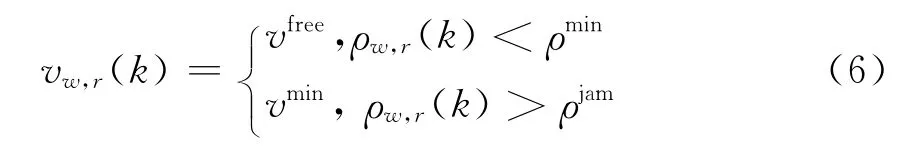
式中：vfree为车辆行驶的自由速度；vmin为车辆行驶的最小速度；ρw，r（k）为第k个采样周期路段（w，r）上车辆的平均密度；ρmin为车辆的最小密度；ρjam为车辆的最大密度．

当车流密度介于最小和最大密度之间时，车流的速度为

2 交叉口协调控制策略

2．1 控制思想

基于路网排队状态均衡的交叉口协调控制思想是根据路网中各个路段的排队状态（排队车辆数占路段可容纳车辆总数的比例）实时动态分配绿灯时间，保证绿灯时间的充分利用，并防止在交通流量不均衡情况下，以总的旅行时间最小为优化性能指标导致部分路段长时间拥堵甚至蔓延到上游交叉口的情况发生．也就是说，如果以路网总的旅行时间最小为优化性能指标，MPC控制器会根据路网中各个路段上的车辆总数分配相应的绿灯时间，这样会使得在交通流量不均衡情况下，交通流量较大的路段长时间占用较多的绿灯时间，而交通流量较小的路段因绿灯时间分配不足使得排队长度不断增长，最终导致该路段长时间拥堵甚至蔓延至上游交叉口．

由于两相位信号交叉口在同一方向的两个进口路段共用同一绿灯时长，因此确定某一相位的绿灯时长需要同时考虑该相位两个进口路段的排队状态，即根据该相位两个进口路段排队状态值较大的路段确定分配的绿灯时长．定义pw，r（k）为路段（w，r）的排队状态值，即

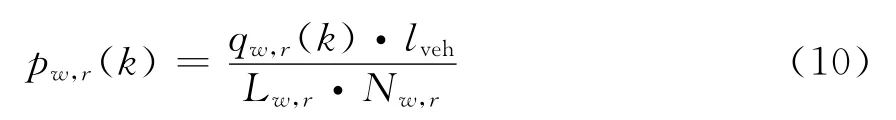
则某一相位的排队状态可由该相位两个进口路段的排队状态值共同决定．以图2交叉口为例，相位1和相位2总的排队状态值为

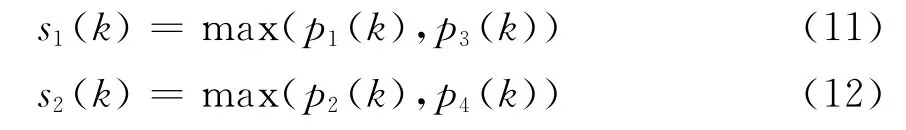
式中：s1（k），s2（k）分别为相位1和相位2的排队状态；pi（k）（i＝1，2，3，4）为交叉口第i个进口路段在第k个周期的排队状态值；max（a，b）为a，b中较大的值．

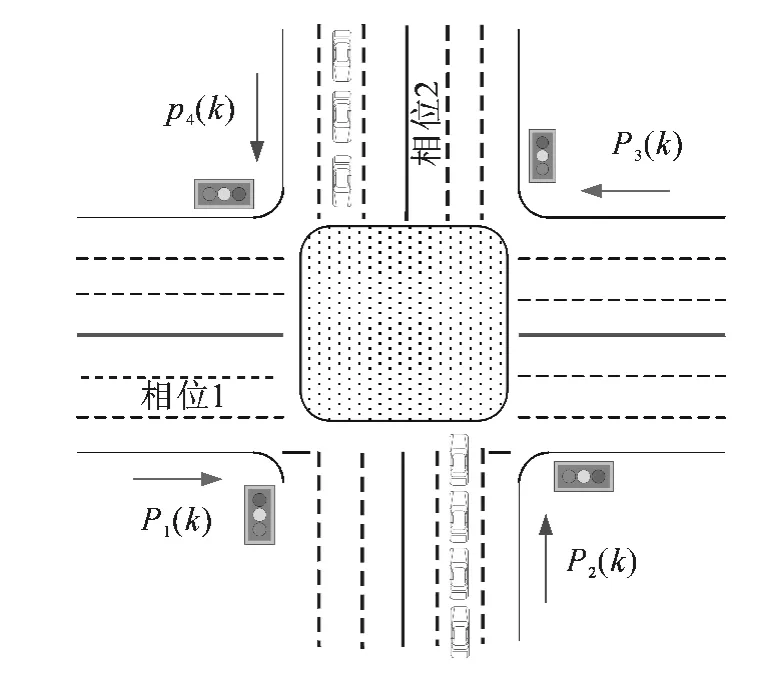
图2 交叉口相位示意图Fig．2 Diagram of intersection phase

2．2 控制策略

模型预测控制是一种基于模型的闭环优化控制策略，其算法的核心是在每个采样周期内预测系统的未来状态，在线反复优化计算并滚动实施控制作用［11］．其中，预测模型的功能是根据系统的历史信息和未来输入预测系统的输出．理论上讲，任何能够反映系统特性并具有预测功能的模型均可作为预测模型使用．但预测模型选取的优劣对MPC的控制效果至关重要．本文利用所提出的排队模型作为MPC的预测模型，对交通网络中各个路段的排队长度进行预测，然后根据路网排队状态均衡的控制策略对交叉口进行协调控制，如图3所示．排队模型可以描述为如下的一般非线性模型为

式中：qw，r（k）为路段的排队长度；dw，r（k）为路网的交通需求；gr（kc）为未来的控制输入．

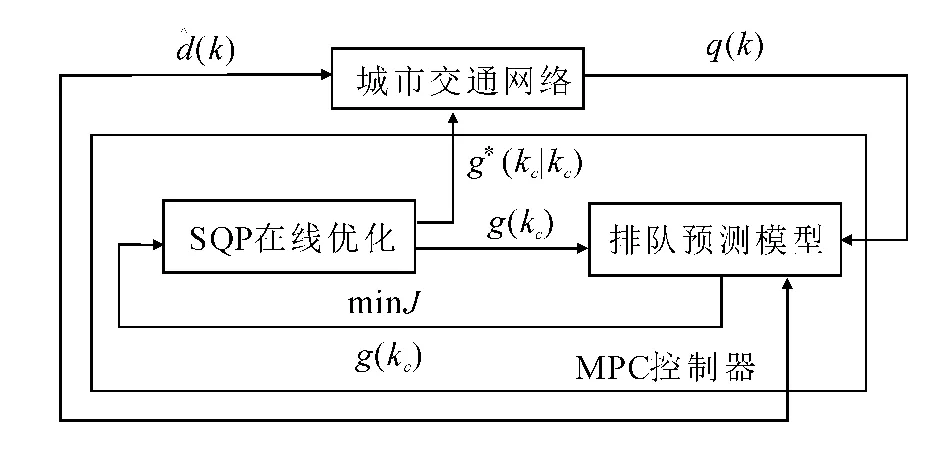
图3 MPC控制器结构图Fig．3 MPC controller structure

基于上述排队模型，则MPC在线优化问题可以描述为

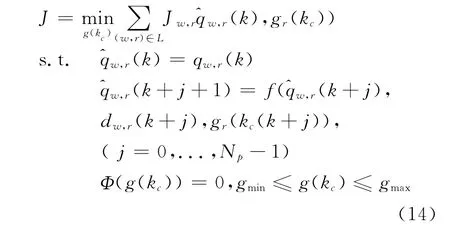
为了提高整个路网的运行效率，充分利用绿灯时间，希望根据路网中各个交叉口相位的排队状态设置绿灯时间，使得各相位的排队长度近似相等，同时消散，因此定义如下优化性能指标为

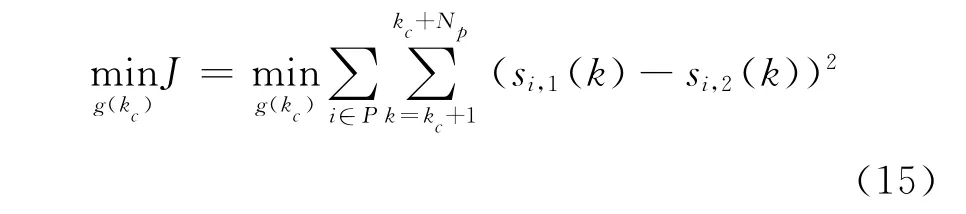
其中P为网络中交叉口集合．

3 仿真

以图4所示路网为例，利用Matlab Vissim软件的集成仿真平台对本文提出的控制策略的有效性进行验证．图中，Sx为路网出行源点．仿真如3种控制方案：① 固定配时方案，其中各交叉口相位的绿灯时长根据韦伯斯特公式计算得到；② 基于文献［10］所提的模型预测控制方案（S-MPC）；③本文所提的模型预测控制方案（P-MPC）．仿真参数定义见表1．

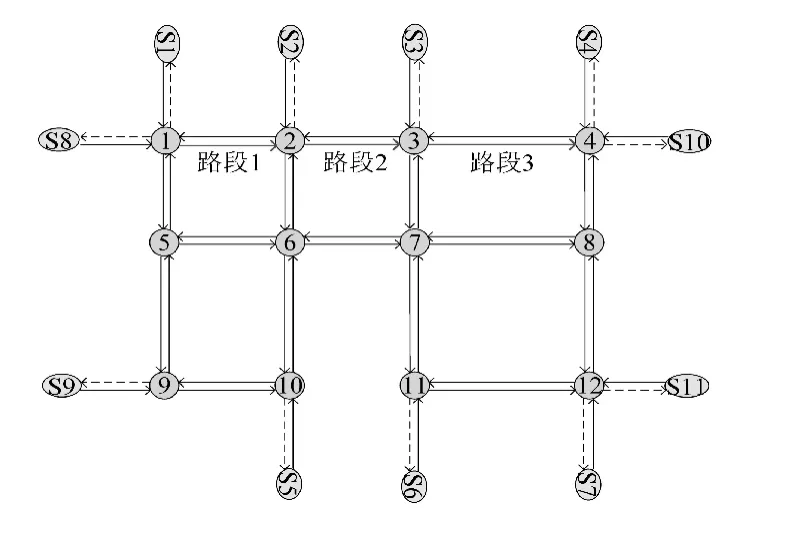
图4 仿真路网Fig．4 The simulation network

表1 仿真参数定义Tab．1 Definition of the simulation parameters

仿真两种交通情形：①欠饱和状态，其中路网出行源点的车辆驶入率均为500辆·h-1；②饱和状态，其中路网出行源点的车辆驶入率随时间变化如图5所示．仿真时间为1h．

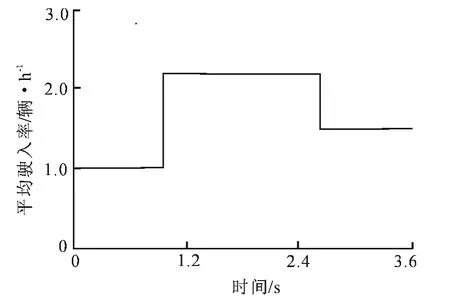
图5 情形2下路网出行源点车辆驶入率Fig．5 Rate of vehicle of road network travel source point in case 2

不同控制方案下车辆在路网中的运行效率可以通过车辆总的延误时间（h）、平均停车次数、车辆速度（km·h-1）及驶离路网的车辆数等指标进行评价．表2给出了不同控制方案下的仿真结果．

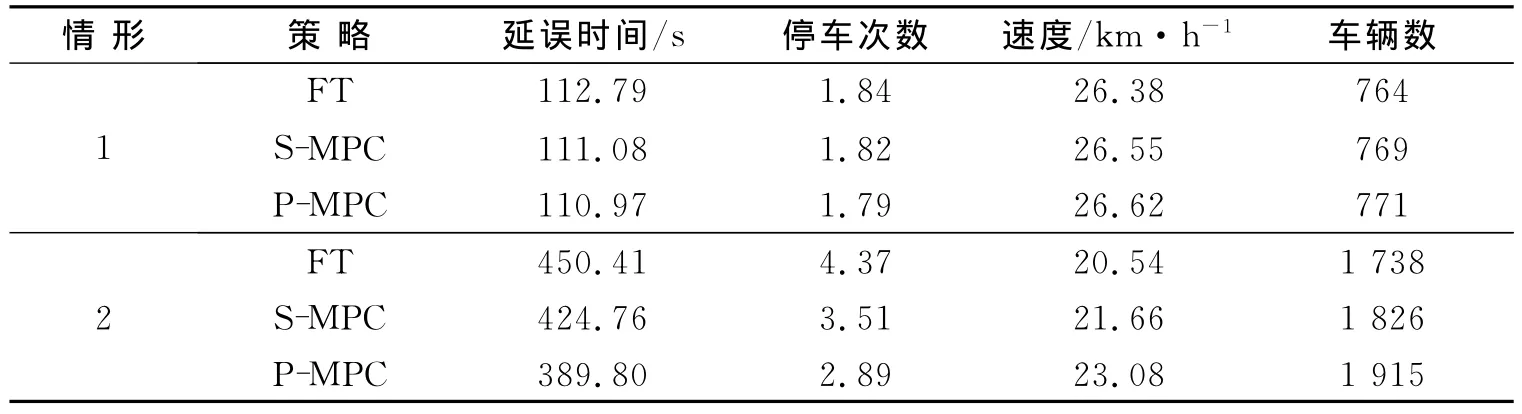
表2 仿真结果Tab．2 Simulation results

从表2的仿真结果可以看出，情形1中3种控制方案下车辆在路网中运行后的指标值相差不大，说明在欠饱和状态下经优化得到的固定配时方案可以较好地匹配路段的交通流量．另外可以看出，与S-MPC控制器相比，P-MPC控制器下的性能指标没有得到明显改善，这是因为在欠饱和状态下路段的车辆密度较小，车辆基本可以按自由流速度行驶，且在交叉口处一个周期的绿灯时间可以得到完全放行，没有较长时间的排队现象发生．但在情形2中，基于模型预测控制的S-MPC和P-MPC控制器下的性能指标明显优于固定配时方案，且PMPC控制器的控制效果优于S-MPC控制器．因为当交通流量较大时，固定配时方案无法根据随机变化的交通状况调整配时方案，使得车辆的延误时间和停车次数大幅增加．而P-MPC控制器可以根据排队模型实时预测各路段的排队长度并进行优化计算得到相应的绿灯时间，使绿灯时间较好地匹配各路段的实际车辆数，从而减少车辆运行的延误时间和停车次数．

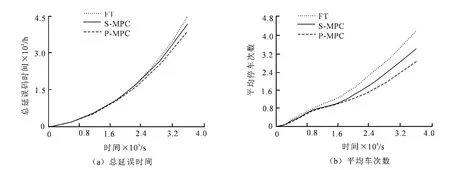
图6 不同控制策略下路网运行效率比较Fig．6 The comparison of network operation efficiency under different control strategies

图6给出了3种不同控制方案下车辆在路网中运行1h后车辆的总延误时间和平均停车次数对比情况．从图6可以看出，在S-MPC和P-MPC两种预测控制器下车辆的总延误时间和平均停车次数均小于固定配时方案，且P-MPC控制器的控制效果明显优于S-MPC控制器．其中，固定配时方案下产生的总延误时间和平均停车车数为450．41h和4．37；而在P-MPC控制器下分别为389．80h和2．89，分别减少13．46%和33．87%．由于排队预测模型是根据路段的车辆密度计算车辆的行驶速度，能更准确地描述实际交通流的动态关系，同时引入基于排队状态均衡的交叉口协调控制思想，使绿灯时间分配更加合理，进而减少因车辆长时间排队产生的延误和停车次数．

为了进一步比较3种控制器下车辆在路网中的运行效率，图7给出了情形2中路段1，2，3上车辆速度随时间的变化情况．从7图中可以看出，与固定配时和S-MPC控制器相比，P-MPC控制器下车辆运行的平均速度最大，说明车辆在路网中具有较高的运行效率．

图7 不同控制策略下车辆速度变化情况Fig．7 The vehicle speed change under different control strategies

4 结 论

为了提高宏观交通流模型的预测精度，改善控制系统的控制性能，本文在考虑车辆行驶速度与密度关系的基础上提出描述路网中交通流动态关系的排队模型，并以此作为预测模型设计了交通信号模型预测控制器．同时还给出了基于排队状态均衡的交叉口协调控制思想，该方法可以使路网内各路段的车辆数得到合理分布进而提高车辆在路网中的运行效率．Matlab-Vissim仿真结果表明，在交通需求充足时，基于排队模型的预测控制器可以有效减少车辆运行的延误时间和停车次数，提高车辆在路网中的运行效率．

［1］ HEUNG T H，HO T K，FUNG Y F．CoordInated Road-Junction Traffic Control by Dynamic Programming［J］．IEEE Transactions on Intelligent Transportation Systems，2005，6（3）：341．

［2］ ABOUDOLAS K，PAPAGEORGIOU M，KOSMATOPOULOS E．Store-and-Forward Based Methods for the Signal Control Problem in Large-Scale Congested Urban Road Networks［J］．Transportation Research Part C：Emerging Technologies，2009，17（2）：163．

［3］ FEBBRARO A DI，GIGLIO D，SACCO N．Urban Traffic Control Structure Based on hybrid Petri Nets［J］．IEEE Transactions on Intelligent Transportation Systems，2004，5（4）：224．

［4］ VAN DEN BERG M，DE SCHUTTER B，HEGYI A，et al．Model Predictive Control for Mixed Urban and Freeway Networks［C］／／Proceedings of the 83rd Annual Meeting of the Transportation Research Board，Washington D C：Transportation Research Board，2004．

［5］ VAN DEN BERG M，HEGYI A，De SCHUTTER B，et al．Integrated Traffic Control for Mixed Urban and Freeway Networks：A Model Predictive Control Approach［J］．European Journal of Transport and Infrastructure Research，2007，7（3）：223．

［6］ HEGYI A，De SCHUTTER B，HELLENDOORN J．Optimal Coordination of Variable speed Limits to Suppress Shock Waves［J］．IEEE Transactions on Intelligent Transportation Systems，2005，6（1）：102．

［7］ VAN DEN BERG M，HEGYI A，DE SCHUTTER B，et al．A Macroscopic Traffic Flow Model for Integrated Control of Freeway and Urban Traffic Networks［C］／／Proceedings of the 42nd IEEE Conference on Decision and Control，Maui（HI）：Proc IEEE Conf Decis Control，2003：2774．

［8］ VAN DEN BERG M，HEGYI A，De SCHUTTER B，et al．Integrated Traffic Control for Mixed Urban and Freeway Networks：A Model Predictive Control Approach［J］．European Journal of Transport and Infrastructure Research，2007，7（3）：223．

［9］ LIN S，De SCHUTTERB，XI Y，et al．Efficient Network-Wide Model-Based Predictive Control for Urban Traffic Networks［J］．Transportation Research Part C：Emerging Technologies，2012，24（1）：122．

［10］ LIU Yue，CHANG G L．An arterial Signal Optimization Bodel for Intersections Experiencing Queue Spillback and Lane Blockage［J］．Transportation Research Part C：Emerging Technologies，2011，19（1）：130．

［11］ 席裕庚，李德伟．预测控制定性综合理论的基本思路和研究现状［J］．自动化学报，2008，34（10）：1225．XI Yu-geng，LI De-wei．Fundamental Philosophy and Status of Qualitative Synthesis of Model Predictive Control［J］．Acta Automatica Sinica，2008，34（10）：1225．（in Chinese）