半掺杂铋基锰氧化物的磁相变和输运性质＊

王 强

（陕西学前师范学院 计算机与电子信息系，西安710100）

钙钛矿结构锰氧化物的一般表达式为Ln1-xDxMnO3（Ln为 La、Pr、Nd和 Bi等三价元素，D为Ca、Sr和Ba等二价碱土元素）．在这些材料中，MnO6八面体晶体结构的畸变通常伴随着一系列奇特的物理现象，如顺磁-铁磁转变，绝缘体-金属转变、电荷有序和自旋有序等［1］．电荷有序是钙钛矿结构锰氧化物中重要实验现象之一，它是电子在实空间局域化的一种特殊形式［2］．在电荷有序态，Mn3＋和Mn4＋离子会自发的在MnO2平面内有序排列，这种空间上的有序排列通常伴随轨道有序和反铁磁转变的发生．因此，电荷有序相的基态一般为反铁磁轨道有序绝缘相．半掺杂锰氧化物电荷有序出现与否以及电荷有序态的稳定性在很大程度上由钙钛矿结构中的A位离子平均半径＜rA＞决定［3］．对于＜rA＞较大的 La1／2Sr1／2MnO3，在较高温度下发生顺磁-铁磁相变，没有电荷有序相出现．当＜rA＞逐渐减小，在较高温度下发生顺磁-铁磁相变逐渐被顺磁态-电荷有序相变所替代．文献［4］认为电荷有序是双条纹结构，电荷在两个子晶格的交替占据，电荷是紧密堆积的；文献［5］认为电荷排列是采取 Wigner晶体形式．在 Wigner晶体结构中，为了减小电荷间的库仑排斥作用，电荷不是紧密堆积的；文献［6］对层状钙钛矿锰氧化物R0．5Sr1．5MnO4电荷有序转变的晶格效应研究发现轨道自由度对电荷有序具有重要影响．

在这些电荷有序锰氧化物中，铋基锰氧化物与稀土锰氧化物性质存在显著的差异．La3＋和Bi3＋离子半径相近，在室温下La1-xCaxMnO3是铁磁金属态，而Bi1-xCaxMnO3是顺磁态且具有很高的电阻［7］．在LaMnO3中，La3＋被二价碱土离子取代可以产生空穴，经由双交换作用引起铁磁性［8-9］；而BiMnO3本身就是铁磁体，空穴掺杂反而抑制其铁磁性［10］．文献［11］对Bi0．3Ca0．7MnO3样品进行锰位Cr掺杂研究，发现了反常磁抗现象．文献［12］对Bi0．5Ca0．5MnO3进行 Co掺杂研究，发现 Co掺杂比Cr掺杂能更有效的破坏 Bi0．5Ca0．5MnO3的电荷有序，这与稀土锰氧化物显著不同．

有关学者对锰氧化物电荷有序做了大量研究，但对电荷有序态的起源问题目前仍不清楚．对具有异常行为的铋基电荷有序锰氧化物进行深入研究，对于理解电荷有序及相关物理现象具有重要的科学意义．电子自旋共振具有高度的灵敏性，是研究磁性材料磁关联的强有力的技术手段．本文通过磁化强度和电子顺磁共振研究Bi0．5Ca0．5MnO3样品磁相变，通过电阻测量研究 Bi0．5Ca0．5MnO3的导电机制及其与磁相转变之间存在的关联，探讨了磁相转变过程中存在的复杂相互作用，为电荷有序产生的物理本质研究提供一定的实验依据．

1 实验材料及方法

1．1 样品的制备

通过传统的固相反应法制备 Bi0．5Ca0．5MnO3多晶样品．按化学计量比分别称取分析纯的Bi2O3、CaCO3和MnO2混合均匀，分别在800℃和900℃预烧并反复研磨均匀，最后在1 000℃烧结并缓慢降至室温，获得所需样品．

1．2 样品的测试

在 MXP18AHF （MAC Science Co．Ltd．，Japan）转靶X射线衍射仪上检验晶体结构和相的纯度．将样品磨成针状，使用超导量子干涉仪SQUID（Quantum Design MPMS-7）来测量样品的宏观磁性．将制备的样品磨成片状长方形，使用物理性质测量系统（型号：Quantum Design PPMS-9）测量其输运性质，电阻测量采用标准的四端引线法．取一定量的粉末样品，用液氮将样品冷却至110K，用电子自旋共振谱仪（型号：JEOL JES-FA200）在9．06GHz的频率下升温测量样品在110～470K温度范围内一些特定温度下的微分吸收谱．

2 结果与讨论

2．1 样品的晶体结构

图1为 Bi0．5Ca0．5MnO3多晶样品在室温时的X射线衍射谱．

图1 Bi0．5Ca0．5MnO3样品的粉末 X射线衍射图Fig．1 Powder X-ray diffraction patterns of Bi0．5Ca0．5MnO3

从图1可以看出，样品没有明显杂峰，所有衍射峰均能用Pnma空间群进行指标化，表明样品为单相正交钙钛矿结构．使用Rietveld方法计算X射线衍射数据得到的晶格参数为a＝0．545nm，b＝0．532nm，c＝0．511nm．

2．2 磁相变和磁有序的磁化强度分析

图2（a）为 Bi0．5Ca0．5MnO3多晶样品零场冷却（Zero-Field-Cooled，ZFC）和 加 场 冷 却 （Field-Cooled，FC）磁化曲线．随着温度的降低，磁化曲线在TCO＝325K出现电荷有序相变峰．在电荷有序态载流子的局域化加强，样品中的双交换作用减弱，反铁磁作用增强．在TN＝130K磁化曲线再次出现峰值，它标志着长程反铁磁有序的形成．在Tf＝35KZFC曲线出现一个尖峰，并且ZFC和FC曲线出现明显的分叉，这是自旋玻璃（Spin-Glass，SG）态的典型特征［13］．

为了进一步研究 Bi0．5Ca0．5MnO3中温度对磁相互作用的影响，利用Curie-Weiss定律（X＝C／（T-θP））对实验数据进行拟合，其中C是居里常数，θP为Curie-Weiss温度．图2（b）为磁化强度倒数（1／M）与温度T 的依赖关系．由图2（b）可以看出，当温度高于TCO，磁化强度曲线满足Curie-Weiss定律，实线是Curie-Weiss定律对其的拟合，拟合得到的Curie-Weiss温度θPH＝148K，为正值，表明高温顺磁态存在由 Mn3＋与 Mn4＋之间的双交换作用引起铁磁相互作用．在电荷有序温度以下，拟合得到的Curie-Weiss温度θPL＝-80K，为负值，说明在电荷有序态反铁磁相互作用增强并占优势．此外，通过实验数据计算得到的有效磁矩μeff分别为3．783μB（T＞TCO）和4．565μB（T＜TCO），它们比理论计算值要大很多，说明高温顺磁区域存在磁团簇现象．这与文献［14］的中子散射结果相一致．由于 Bi0．5Ca0．5MnO3中存在铁磁有序和反铁磁有序的竞争，导致在低温下出现自旋玻璃态．

图2 Bi0．5Ca0．5MnO3样品在1kOe磁场下磁化强度随温度的变化曲线Fig．2 Temperature dependence of magnetization of Bi0．5Ca0．5MnO3sample at H＝1kOe

2．3 磁相变和磁有序的电子自旋共振分析

样品的宏观磁性也可以反映到微观磁性上．为了研究样品的微观磁性，测试了在一些特定温度下电子自旋共振谱的一次微分曲线，它们均是单一对称的洛仑兹线型．朗德因子g可以用来研究材料磁相的转变．不同温度下电子自旋共振曲线的朗德因子g表达式为

式中：h为普朗克常数；v为微波频率；μB为玻尔磁子；Hres为共振磁场强度．

图3（a）给出了朗德因子g随温度变化的曲线．当温度由470K降低到TCO＝325K时，g因子几乎不随温度发生变化，表明在电荷有序温度以上的高温顺磁区域存在铁磁相互作用．当温度从TCO降低到TO（约150K），g因子首先迅速增大，继而在一定温度范围保持不变，然后继续增加．在电荷有序温度以下，g因子随温度的变化可能与自旋-轨道耦合以及晶体场的劈裂有关．g因子在一定温度范围几乎保持不变，表明了自旋、晶格、电荷及轨道自由度之间的精细平衡．当温度低于TO，g因子急剧减小．g因子在低温下的急剧减小与长程反铁磁序 的 开 始 有 关，这 种 现 象 在 La0．21Pr0．49Ca0．3MnO3和 Nd0．5Sr0．5MnO3中也有报道［15］．

图3（b）给出了共振线宽ΔHpp随温度变化曲线．在高温区域，随着温度的降低，共振线宽ΔHpp线性减小并在TCO＝325K达到最小值．共振线宽ΔHpp的线性减小通常归因于“瓶颈”自旋-晶格驰豫机制．“瓶颈”自旋-晶格驰豫模型认为电子自旋共振信号来源于Mn3＋和Mn4＋组成的复杂磁性团簇，这些磁性团簇与晶格之间存在相互作用［16］．正是这种“瓶颈”自旋-晶格相互作用减小引起了ΔHpp线性减小．随着温度的进一步降低，ΔHpp随温度的变化与g因子相似．当体系由顺磁态转变到另一磁有序态，ΔHpp会随温度的降低急剧增大．因此，在电荷温度以下，ΔHpp随温度的降低迅速增大，可能与反铁磁有序的增强有关．电荷有序转变同时伴随eg电子的轨道有序的发生，导致低温下ΔHpp又一次迅速增大．在TCO以下，ΔHpp随温度的降低逐渐增加是电荷有序锰氧化物的典型特征．当温度低于TO，ΔHpp突然降低，这与低温下长程反铁磁态的形成相一致．

电子自旋共振谱强度I可以通过对一次微分电子自旋共振谱进行两次积分得到，图3（c）给出了归一化的积分强度I随温度变化的关系曲线．电子自旋共振强度I随着温度的降低增加，并在TCO＝325K出现一个宽的电荷有序转变峰，这与磁化强度研究结果相一致．对 Bi0．5Ca0．5MnO3的磁化强度研究表明：该体系在顺磁相存在铁磁自旋关联；当进入电荷有序态时，铁磁自旋关联被反铁磁自旋关联压制．正是由于铁磁自旋关联和反铁磁自旋关联的竞争使得电子自旋共振强度曲线上形成宽的电荷有序相变峰．在电荷有序相变温度以下，电子自旋共振强度的迅速减小是由于反铁磁自旋关联的逐渐增强．随着温度的进一步降低，电子自旋共振强度继而在一定温度范围内保持不变，当温度低于TO，电子自旋共振强度迅速下降．在反铁磁相变温度TN以下，电子自旋共振强度变得非常微弱且不随温度变化．这是由于用于探测反铁磁所需要的磁场比电子自旋共振测量所加磁场要高得多，故电子自旋共振不能直接探测到反铁磁态．

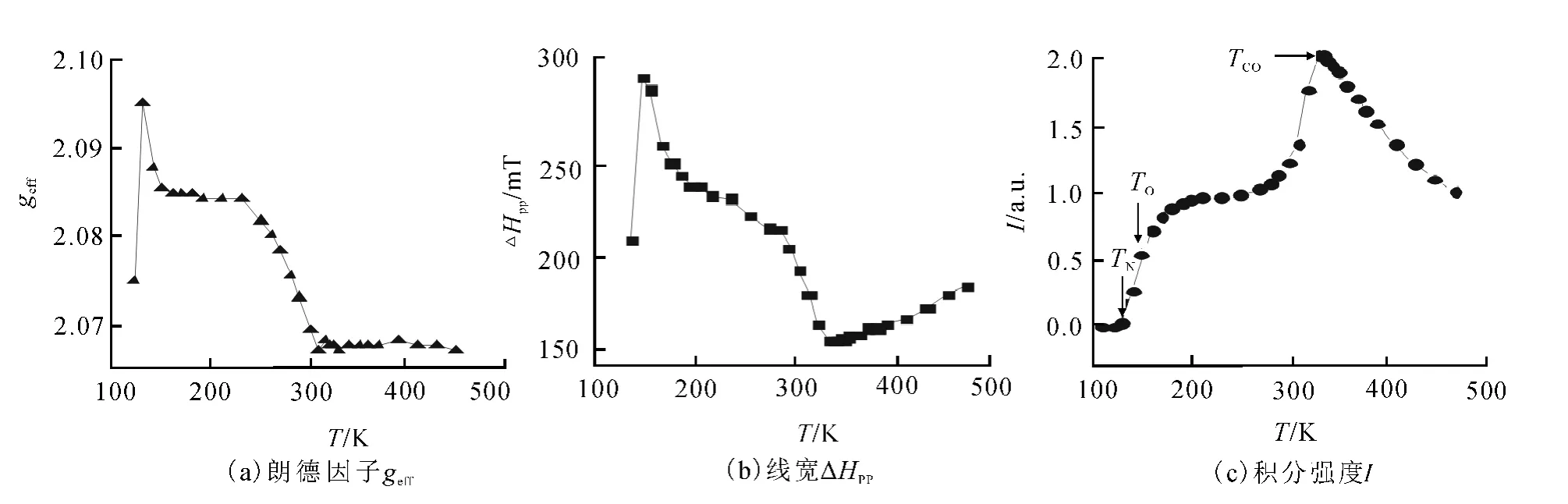
图3 Bi0．5Ca0．5MnO3样品电子自旋共振参数随温度的变化曲线Fig．3 Temperature dependence of the electron-spin-resonance parameters of Bi0．5Ca0．5MnO3sample

2．4 磁相变的输运性质分析

图4（a）为零场下样品在90～380K温度范围内电阻率ρ与温度T关系曲线．在整个测量温区，电阻率随温度的降低而升高，表现为半导体的输运性质．在TCO附近，电阻率出现突然迅速的增大，这与样品进入电荷有序相有关．在电荷有序相，高温巡游的eg电子随着温度的降低跳跃动能减小，并在MnO2平面内有序排列形成自发电子局域化，因此电阻率在电荷有序相转变处迅速增大．随着温度的继续下降，电子局域化倾向程度加强，电阻率继续升高．由于电荷的局域化引起的半导体输运行为通常能用小极化子近邻跃迁模型（lnρ／T-1 000／T）和 Mott 可 变 程 跃 迁 模 型 （lnρ-1／T-1／4）来描述［17］．

利用两种模型对样品在零场下ρ-T曲线进行了拟合，结果如图4（b）～（c）所示．小极化子近邻跃迁模型lnρ／T-1 000／T 存在较大的偏差，样品的电阻率很好地符合可变程跃迁机制．对于小极化子，电子在跃迁过程中，其周围的晶格畸变（Jahn-Teller极化子）随电子的跃迁一起运动，eg电子需要通过热激活的方式才能在格点间发生跃迁．在Bi0．5Ca0．5MnO3样品中，Bi3＋高度极化的6s2孤对电子引起的局部晶格畸变甚至导致Bi-6S轨道和O-2P轨道的杂化，使载流子处于强局域化状态，热激发能量不足以使电子跳到最近邻位置，电子将倾向于跳到相距较远而能量相差又较小的其他局域态中．由于这种跃迁中跳跃步长随温度的降低而增大，故称之为变程跃迁．在Mott变程跳跃模型中，主要是考虑材料中载流子由于磁无序的影响而建立的．在高温区域，lnρ-1／T-1／4曲线在TCO突然迅速增加而偏离了线性，标志着电荷有序转变的发生；当温度低于TN，lnρ-1／T-1／4曲线斜率突然增大，这可能与自旋相关的输运机制有关．在顺磁态，Mn位磁矩取向是无序的；在反铁磁态，近邻Mn位磁矩是反平行排列的．这使得eg电子在反铁磁态的跃迁比在顺磁态更加困难，从而导致电阻率在TN以下迅速增加［17］．

图4 Bi0．5Ca0．5MnO3样品的电阻率与温度关系曲线Fig．4 Temperature dependence of resistivity of Bi0．5Ca0．5MnO3sample

3 结 论

利用传统固相反应法制备 Bi0．5Ca0．5MnO3多晶样品．通过测量磁化强度、电子顺磁共振谱和电阻与温度的依赖关系，研究了 Bi0．5Ca0．5MnO3的磁相变特征及其与输运行为之间的关联．得到结论为

1）磁化强度研究表明，在高温顺磁态Bi0．5Ca0．5MnO3中存在弱的铁磁自旋关联；在电荷有序态（TCO＝325K），铁磁自旋关联被反铁磁自旋关联压制，并在反铁磁相变温度TN＝130K形成长程反铁磁有序．由于铁磁有序和反铁磁有序竞争，零场冷却和加场冷却磁化曲线在Tf＝35K出现明显分叉，表明在低温下形成的自旋玻璃态．

2）电子自旋共振研究与磁化强度研究结果相一致，并能反映自旋、晶格、电荷及轨道自由度之间的精细平衡．在高温顺磁态，由于“瓶颈”自旋-晶格驰豫机制，导致线宽的线性减小；电荷有序转变同时伴随着自旋-轨道耦合以及晶体场的劈裂．

3）在90～380K温度范围内，零场下电阻率表现为半导体输运性质，符合Mott可变程跃迁模型，并能显示电荷有序和反铁磁相变特征，这与自旋相关的输运机制有关．

［1］ SALAMON M B，JAIME M．The Physics of Manga-nites：Structure and Transport［J］．Reviews of Modern Physics，2001，73（3）：583．

［2］ TOMIOKA Y，OKUDA T，OKIMOTO Y．Charge／Orbital Ordering in Perovskite Manganites［J］．Journal of Alloys and Compounds，2001，326（26）：27．

［3］ DAGOTTO E，HOTTA T，MOREO A．Colossal Magnetoresistant Materials：The Key Role of Phase Separation［J］．Physics Reports，2001，344（1／3）：1．

［4］ MORI S，CHEN C H，CHEONG S W．Pairing of Chargeordered Stripes in （La，Ca）MnO3［J］．Nature，1998，392（6675）：473．

［5］ RADAELLI P G，COX D E，CAPOGNA L，et al．Wigner-crystal and Bi-sBodels for the Magnetic and Crystallographic Superstructures of La0．33Ca0．67MnO3［J］．Physical Review B，1999，59（22）：14440．

［6］ MORITOMO Y，NAKAMURA A，MORI S，et al．Lattice Effects on the Charge-ordering Transition in R0．5Sr1．5MnO4［J］．Physical Review B，1997，56（23）：14879．

［7］ WOO H，TYSON T A，CROFT M，et al．Correlations Between the Magnetic and Structural Properties of Ca-Doped BiMnO3［J］．Physical Review B，2001，63（13）：134412．

［8］ DE GENNES P G．Effects of Double Exchange in Magnetic Crystals［J］．Physical Review，1960，118（1）：141．

［9］ ANDERSON P W．HASEGAWA H．Considerations on Double Exchange［J］．Physical Review，1955，100（2）：675．

［10］ CHIBA H，ATOU T，SYONO Y J．Magnetic and E-lectrical Properties of Bi1-xSrxMnO3：Hole-doping Effect on Ferromagnetic Perovskite BiMnO3［J］．Solid State Chemistry，1997，132（1）：139．

［11］ ZHANG R R，KUANG G L，YIN L H，et al．Magnetization Reversal in the Cr-doped Manganite Bi0．3Ca0．7Mn0．75Cr0．25O3［J］．Journal of Alloys and Compounds，2012，519 （4）：92．

［12］ 王强．Bi0．5Ca0．5Mn1-xCoxO3体系中的电荷有序和相分离［J］．物理学报，2010，59（9）：6569．WANG QIANG．Charge Order and Phase Separation in Bi0．5Ca0．5Mn1-xCoxO3system［J］．Acta Physica Sinica，2010，59（9）：6569．（in Chinese）

［13］ BINDER K，YOUNG A P．Spin Glasses：Experimental Facts，Theoretical Concepts，and Open Questions［J］．Reviews of Modern Physics，1986，58（4）：801．

［14］ BAO W，AXE J D，CHEN C H，et al．Impact of Charge Ordering on Magnetic Correlations in Perovskite （Bi，Ca）MnO3［J］．Physical Review Letter，1997，78（3）：543．

［15］ AUTRET C，GERVAIS M，GERVAIS F，et al．Signature of Ferromagnetism，Antiferromagnetism，Charge Ordering，and Phase Separation by Electron Paramagnetic Resonance Study in Rare Earth Manganites，Ln1-xAxMnO3（Ln＝ Rare Earth Element，A ＝ Ca，Sr） ［J］．Solid State Science，2004，6（8）：815．

［16］ SHENGELAYA A，ZHAO G M，KELLER H，et al．EPR in La1-xCaxMnO3：Relaxation and Bottleneck［J］．Phys Rev B，2000，61（9）：5888．

［17］ 李仁文，屈哲，张蕾，等．Ba2＋掺杂钙钛矿 Bi0．5Ca0．5MnO3多晶材料的结构、磁性和输运性质研究［J］．低温物理学报，2011，33（2）：81．LI Ren-wen，QU ZHE，ZHANG Lei，et al．Structure，Magnetic and Transport Properties in Ba2＋Doped Perovskite Manganites Bi0．5Ca0．5MnO3［J］．Chinese Journal of Low Temperature Physics，2011，33（2）：81．（in Chinese）

【相关参考文献链接】

白岗，答元，刘涛．热处理条件对NdFeB纳米复合材料磁性能的影响［J］．2008，28（5）：449．

白岗，答元，刘涛．Pr和Co的添加对NdFeB纳米复合永磁材料磁性能的影响［J］．2009，29（4）：345．

白岗，答元，刘涛．Nd8-xDyxFe82Co6B4纳米复合永磁材料的磁性能［J］．2011，31（4）：318．

郑德山．γ-MnO2纳米六方片的磁性特性研究［J］．2012，32（6）：465．

郭宝亿，谭宝成，张峰．基于ARM的热敏电阻测温模块设计［J］．2009，29（4）：361．

坚增运，杨晓琴，魏超锋，等．从液态镓的电阻率研究其结构变化的滞后性［J］．2009，29（5）：437．

常芳娥，李卫军，吕士勇，等．从液态锡的电阻率研究其结构变化的滞后性［J］．2010，30（2）155．

周顺，刘卫国，蔡长龙，等．电阻阵列红外景物产生器微桥结构的研制及仿真［J］．2012，32（8）：613．