谐振法测量损耗卡尔曼滤波数据处理＊

闫丽荣，高爱华，杨 捷

（西安工业大学 陕西省薄膜技术与光学检测重点实验室／光电工程学院，西安710021）

光学谐振腔是激光陀螺和激光器的核心组成部分，其损耗的大小直接关系到陀螺和激光器的性能和精度．谐振腔的损耗主要包括谐振腔衍射损耗及膜片损耗．精确测量谐振腔损耗的大小是指导激光陀螺、激光器生产的重要手段，对提高激光陀螺、激光器的性能和精度具有重要的指导意义．

目前光学谐振腔损耗可以用谐振法和时间衰减法来进行测量．在实际损耗测量装置的研制过程中发现，影响损耗测量精度的因素众多，除了优化装置各部分的硬件以外，在实际测量中利用软件对测量的数据进行处理可以提高在现有硬件设备条件下测量的准确性，从而减小测量误差．近年来众多研究单位相继加入损耗检测的研究中，文献［1］最早进行了谐振腔超低损耗测量方面的研究；文献［1-2］提出了小抖动稳频技术，该技术是通过调制激光光强使得激光频率被锁定在与谐振腔谐振的某个频率上，采用锁相方式获得光强的相位和幅值随调制信号频率的变化曲线，拟合获得衰荡时间，进而确定谐振腔损耗；文献［1-2］相继进行了吸收光谱和高反射率方面的研究，获得的反射率测量精度可达10-5量级；文献［3］设计了一套实时测量谐振腔损耗系统，完成了系统功能仿真．但对于提高测量精度都只是原理及优化硬件方面的研究，还没有利用软件的方法优化损耗检测系统．

卡尔曼滤波是一种高效的处理动态数据的方法［4-8］，可以有效过滤噪声，获得测量最优估计值．它是以最小均方误差为估计的最佳准则，来寻求一套递推估计的算法，其基本思想是：采用信号与噪声的状态空间模型，利用前一时刻的估计值和现时刻的观测值来更新对状态变量的估计，求出现时刻的估计值．它适合于实时处理和计算机运算．卡尔曼滤波的实质是由量测值重构系统的状态向量．它以“预测-实测-修正”的顺序递推，根据系统的量测值来消除随机干扰，再现系统的状态，或根据系统的量测值从被污染的系统中恢复系统的本来面目．综上所述，使用卡尔曼滤波作为在软件上优化损耗测量系统的方法以滤除噪声是可行的．

为了提高谐振法损耗测量的准确性，本文研究了在Labview环境下利用卡尔曼滤波处理损耗测量数据以降低其测量误差的方法，提高了测量的信噪比．

1 谐振法腔体损耗测量原理

通过改变注入被研究谐振腔激光的频率，使得被测谐振腔产生振荡输出．当注入激光的频率与谐振腔的固有频率匹配时，光强达到最大值．对谐振腔光谱分析可知，频谱宽度与损耗的关系为

式中：Δv为频谱的宽度；c为光速；δ为谐振腔损耗；L为谐振腔的腔长．谐振曲线宽度是功率谱的半高宽度，测量谱线的半宽度即可得到谐振腔的损耗［9-10］．

如果在一定时间t内，按照线性规律改变注入激光的频率，并观察经过谐振腔振荡输出的功率信号，就可以得到与谐振腔固有模式相符的谐振腔振荡功率随时间变化曲线，从而得到如图1所示的谱线图，频谱宽度Δv与时间变化量Δt对应，纵模间隔与时间T对应，于是可以得到

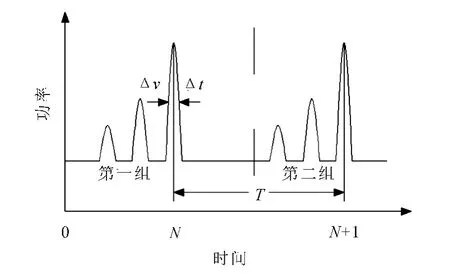
图1 功率谱曲线图Fig．1 Power spectrum graphs

谐振法损耗测量系统示意图如图2所示．主控计算机通过控制压电陶瓷电源进而改变腔长实现激光的输出频率变化，激光经过模式匹配系统进入光学谐振腔中，当达到光学耦合时，其光强会达到最大，通过实时采集系统采集进入系统的信号，利用Labview软件进行数据处理．

系统在测量前设定谐振腔腔长L与激光器腔长Ls等已知量，通过测得两组模之间的时间差T及模半高宽Δt，即可计算出该谐振腔的对应模损耗．由于各种噪声的干扰导致谐振法损耗测量值波动较大，因此需要一种数据处理方法优化噪声进而得到更精确的损耗值．

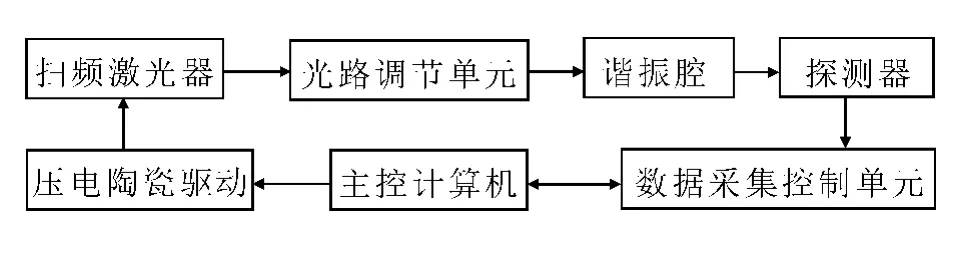
图2 损耗测量系统框图Fig．2 Block diagram of loss measurement system

2 卡尔曼滤波理论模型及软件设计

2．1 卡尔曼滤波理论模型

卡尔曼滤波理论是根据已知信号的观测值通过借助数学的方法去预估最符合系统下一状态真值的最优估计．它是一种时域滤波方法，采用状态空间方法描述系统，算法采用递推形式，数据存储量小，不仅可以处理平稳随机过程，也可以处理多维和非平稳随机过程．离散型卡尔曼滤波基本方程为

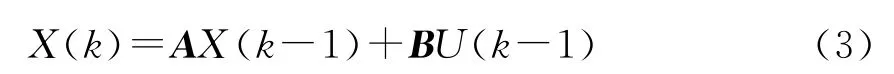
式中：X（k）为利用上一状态预测的结果；X（k-1）为上一状态最优的结果；U（k）为p维随机过程噪声序列；A为n×n维非奇异状态tk-1时刻至tk时刻的一步转移阵；B为n×p维系统过程噪声输入矩阵．

对X（k）的量测满足线性关系，量测方程为

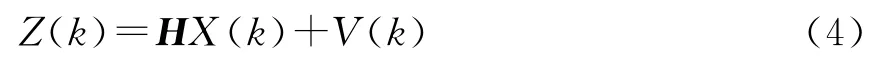
式中：H为m×n维量测阵；V（k）为m维系统随机量测噪声序列．

如果被估计状态X（k）满足式（3），量测量Z（k）满足式（4），且系统噪声U（k）和量测噪声V（k）为零均值或非零均值的白噪声或高斯白噪声随机过程序列，方差阵各为Q（k）和R（k），系统方差阵Q（k）非负定，量测方差R（k）正定，k时刻的量测为Z（k），则X（k）的估计＾X（k）按离散型卡尔曼滤波基本方程方程［5-9］求解，表达式为

在一个滤波周期内，从卡尔曼滤波在使用系统信息和量测信息的先后次序来看，卡尔曼滤波具有两个明显的信息更新过程，时间更新过程和量测更新过程．

对于单模型单测量，I＝1．当系统进入k＋1状态时，卡尔曼滤波算法就可以自回归的运算下去．

2．2 虚拟卡尔曼滤波器设计

结合谐振法损耗测量系统，考虑一维系统，状态方程和量测方程为

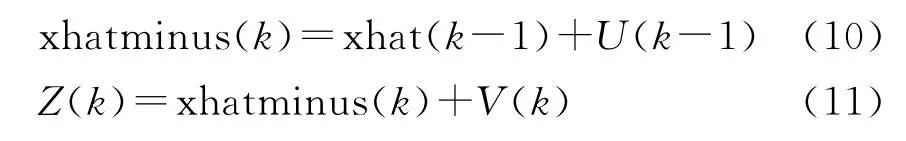
式中：xhatminus（k）为损耗的先验估计，即在k-1时刻，对k时刻损耗做出的估计；Z（k）为损耗的测量值；U（k-1）和V（k）为互不相关的零均值白噪声序列，方差分别为Q和R．

依据离散型卡尔曼滤波基本方程获得实际测量数据卡尔曼滤波处理算法为

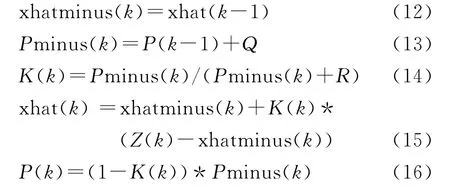
式中：xhat（k）损耗的后验估计，即在k时刻，结合当前损耗测量值与k-1时刻先验估计，得到的最终估计值；P（k）为后验估计的方差；Pminus（k）先验估计的方差；K（k）为卡尔曼增益，反应了损耗测量结果与过程模型的可信程度．

算法依据初始值和量测Z（k）数据进行滤波计算，滤波计算循环的次数由量测数据的个数来决定．卡尔曼滤波计算步骤为

①k＝0，根据测量值得到初始最优估计值xhat（0）和对应的方差P0；

② 下一时刻k＝1，由上一时刻的最优估计值结合式（12）得到当前时刻的先验估计值xhatminus（k），依据式（13）结合上一时刻最优估计值对应的方差P0获得当前时刻的先验估计的方差Pminus（k），依据式（14）结合先验估计方差得到卡尔曼增益K（k）；

③ 依据式（15）和式（16）结合以上步骤中获得的数值及测量值得到时刻k＝1时损耗的后验估计xhat（k）和对应的后验估计方差P（k）；

④k＝k＋1，重复以上步骤，得到每个时刻测量值的最优估计值和对应的最优估计方差．

依据以上算法，基于Labview软件平台设计了卡尔曼滤波器，其程序如图3所示．程序通过设定系统方差Q，测量方差R，初始估计以及初始均方误差P等初始参数，即可实现一维数据的卡尔曼滤波．

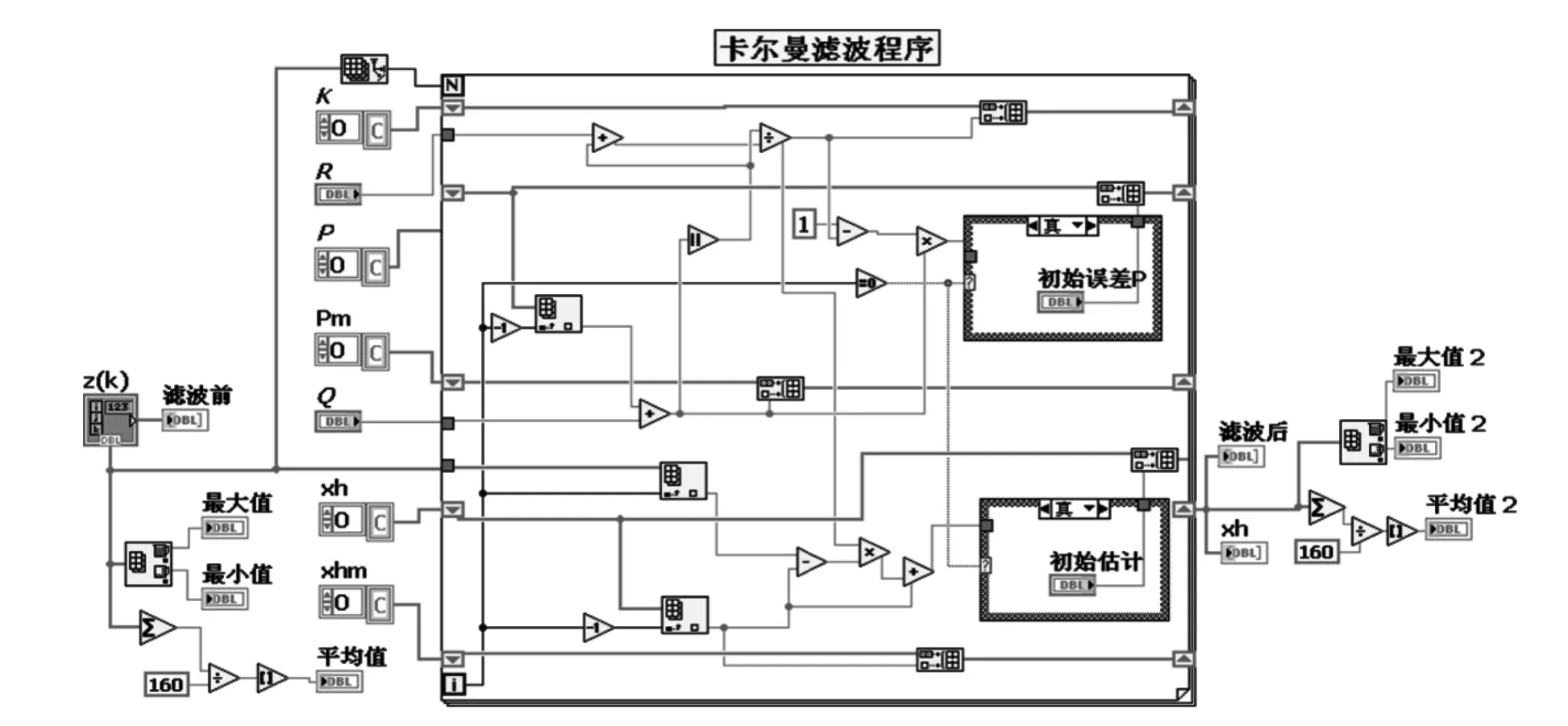
图3 卡尔曼滤波程序面板Fig．3 Kalman filtering program panel

3 数据处理分析

使用谐振法损耗测量系统对谐振腔损耗进行测量，谐振腔每经历一个周期可以测得一组损耗值，获取3号模的160个损耗原始数据，损耗数值均乘以10-6，数据见表1．

依据表1损耗测量数据获得系统方差Q为9×10-6、初始估计（平均值）为1．038×10-3、初始误差P为1．29×10-4，测量方差R为2．5×10-4等卡尔曼滤波初始设定值．设置初始值对损耗测量数据进行卡尔曼滤波处理，滤波后获取的最佳估计数据见表2，测量数据滤波前后对比如图4所示．

由图4可以看出，卡尔曼滤波前损耗最大值为1．315×10-4、最小值为8．57×10-3、平均值为1．038×10-3、误差范围是±2．77×10-4；滤波后最大值为1．197×10-3、最小值为8．85×10-4、平均值为1．034×10-3、误差范围是±1．63×10-4．未经过卡尔曼滤波时噪声跳动对损耗测量影响较大，经过了滤波处理之后损耗值更为可靠，结果显示系统的稳定性及误差都得到了改善．

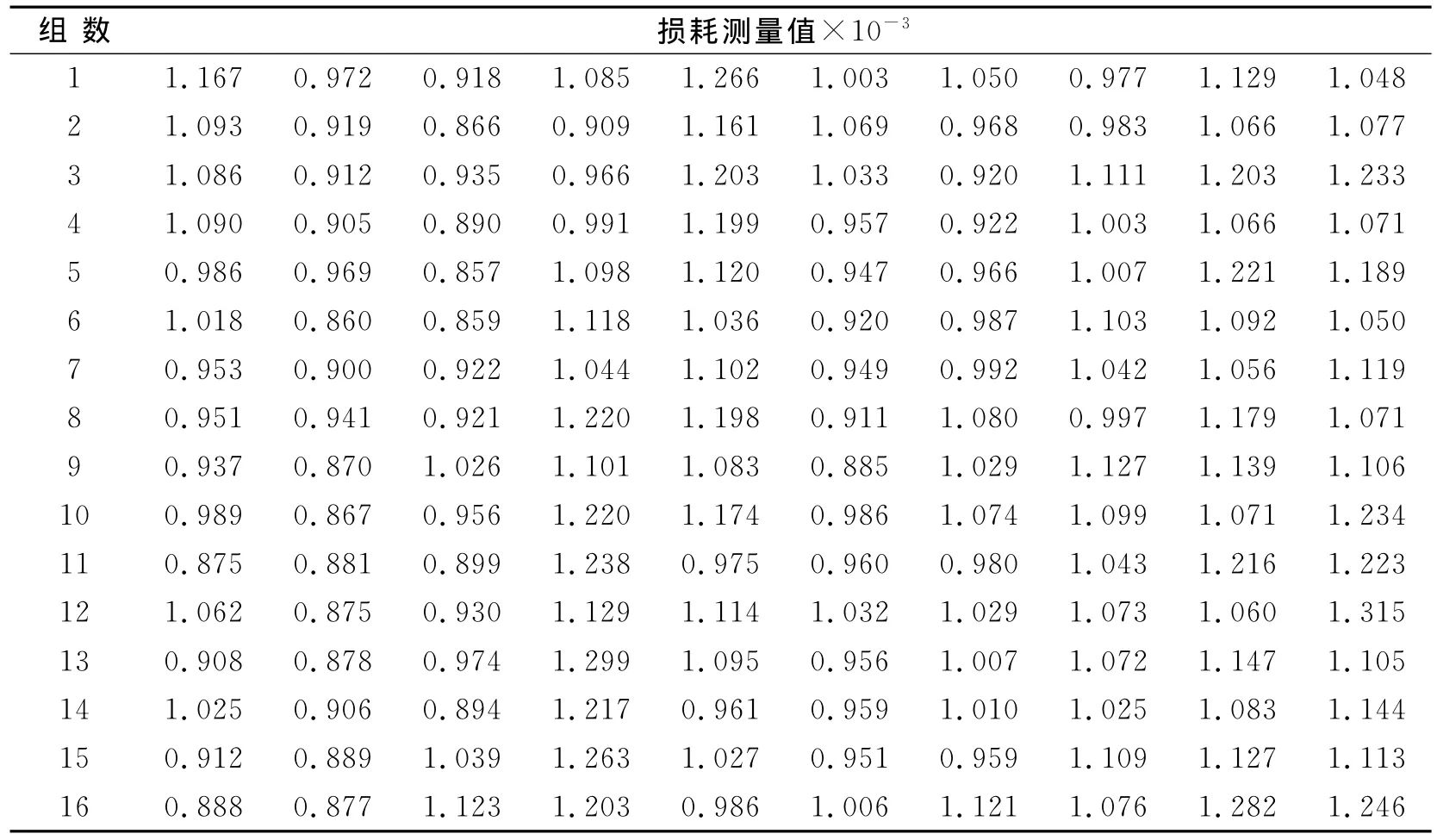
表1 3号模损耗数据Tab．1 Loss data of the 3rd mode

表2 经过卡尔曼滤波之后的3号模损耗数据Tab．2 Loss data of the 3rd mode after kalman filtering

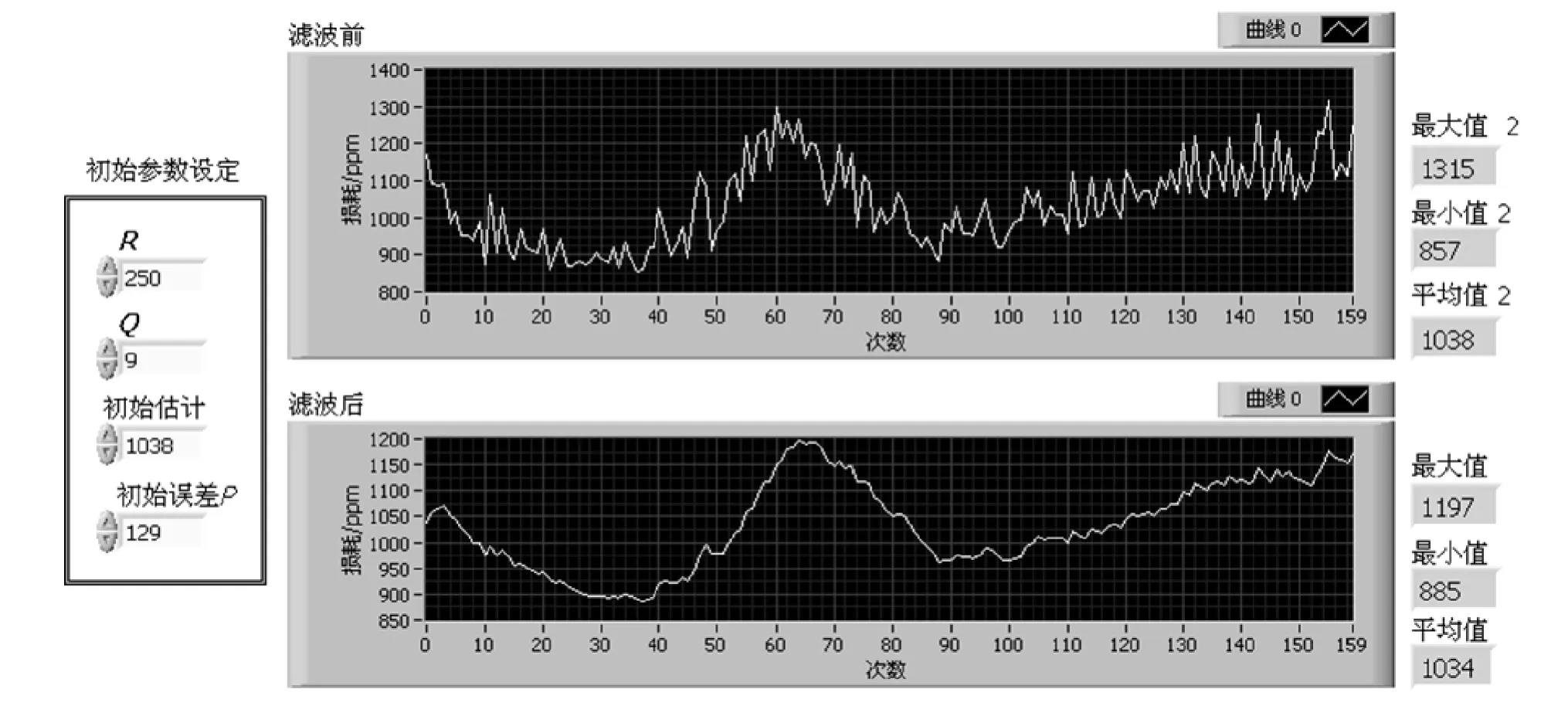
图4 卡尔曼滤波器滤波前后对比图Fig．4 Comparison chart before and after filtering

4 结 论

1）提出了一种基于卡尔曼滤波的谐振法损耗测量数据处理方法，该方法对提高损耗测量系统的精度具有实用参考价值．

2）利用Labview软件编程设计了卡尔曼滤波程序，并对160个3号模的损耗值进行卡尔曼滤波处理及分析，未处理时，误差范围为±2．77×10-4，处理后，误差范围为±1．63×10-4．

3）采用卡尔曼滤波对损耗测量数据进行处理是有效的，它减少了噪声对测量值的影响，提高了系统测量精度．卡尔曼滤波为谐振法损耗测量系统的数据处理和分析提供了一个新的思路．

［1］ 王锐．光腔衰荡法光学谐振腔损耗仪的研究［D］．西安：西安电子科技大学，2011．WANG Rui．Losses Measurement of Optical Cavity Based on Cavity Ring-down Method［D］．Xi’an：Xidian University，2011．（in Chinese）

［2］ 唐常云．激光谐振腔损耗测量系统测控软件的设计与实现［D］．南京：南京理工大学，2013．TANG Chang-yun．Design and Implementation of Laser Resonator Loss Measuring System Control Software［D］．Nanjing：Nanjing University，2013．（in Chinese）

［3］ 宿美春．激光陀螺谐振腔损耗测量［D］．西安：西安电子科技大学，2009．SU Mei-chun．Losses Measurement of Laser Gyroscope Cavity［D］．Xi’an：Xidian University，2009．（in Chinese）

［4］ WELCH G，BISHOP G．An Introduction to the Kalman Filter［R］．New York：Acm，2001．

［5］ 邱凤云．Kalman滤波理论及其在通信与信号处理中的应用［D］．济南：山东大学，2008．QIU Feng-yun．Kalman Filtering with its Application to Communication and Signal Processing［D］．Jinan：Shandong University，2008．（in Chinese）

［6］ 秦永元，张洪钺，汪叔华．卡尔曼滤波与组合导航原理［M］．西安：西北工业大学出版社，1998．QIN Yong-yuan，ZHANG Hong-yue，WANG Shu-hua．Kalman Filtering and Navigation Principles［M］．Xi’an：Northwestern Polytechnical University Press，1998．（in Chinese）

［7］ 邓自立．卡尔曼滤波与维纳滤波［M］．哈尔滨：哈尔滨工业大学出版社，2001．DENG Zi-li．Kalman Filter and Wiener Filter［M］．Harbin：Harbin Institute of Technology Press，2001．（in Chinese）

［8］ 戴洪德，周绍磊，戴邵武，等．卡尔曼滤波及其实时应用［M］．北京：清华大学出版社，2013．DAI Hong-de，ZHOU Shao-lei，DAI Shao-wu，et al．Kalman Filtering with Real-time Applications［M］．Beijing：Tsinghua University Press，2013．（in Chinese）

［9］ 邹志勇，高爱华，李超良．谐振腔损耗曲线拟合［J］．半导体光电，2012，33（6）：838．ZOU Zhi-yong，GAO Ai-hua，LI Chao-liang．Study on Curve-fitting for Resonant Cavity Loss［J］．Semiconductor Optoelectronics，2012，33（6）：838．（in Chinese）

［10］ 田海峰，秦瑞，李路且．激光陀螺谐振腔损耗与相位差测量［J］．中国惯性技术学报，2006，14（4）：85．TIAN Hai-feng，QIN Rui，LI Lu-qie．Losses and Phaseshift Measurement of Laser Gyroscope Cavity［J］．Journal of Chinese Inertial Technology，2006，14（4）：85．（in Chinese）

【相关参考文献链接】

肖秦琨，雷斌．基于卡尔曼滤波的摄像头目标跟踪［J］．2006，26（1）：1．

王航宇，倪原．基于卡尔曼滤波器的电动汽车PID控制系统设计［J］．2008，28（3）：267．

穆静，蔡远利，王长元．基于L-M方法的迭代容积卡尔曼滤波算法及其应用［J］．2013，33（1）：1．

穆静，陈芳．似然迭代平方根容积卡尔曼滤波算法的克拉美罗下界分析［J］．2014，34（7）：536．