双薄壁高墩曲线多跨连续刚构桥自振特性分析

李 杰， 周明坤， 陈 淮

(郑州大学 土木工程学院 河南 郑州 450001)



双薄壁高墩曲线多跨连续刚构桥自振特性分析

李 杰， 周明坤， 陈 淮

(郑州大学 土木工程学院 河南 郑州 450001)

为确定双薄壁高墩曲线多跨连续刚构桥的自振特性，以某双薄壁高墩曲线五跨连续刚构桥为实例，应用ANSYS有限元软件中的Solid 65实体单元和Beam 188梁单元建立该桥空间有限元计算模型，同时利用Midas/Civil建立大桥空间梁单元有限元模型，探讨不同软件、不同单元类型以及预应力张拉对双薄壁高墩曲线多跨连续刚构桥自振频率的影响，分析曲线桥梁结构的平曲线半径对双薄壁高墩曲线连续刚构桥的自振特性的影响，最后按照桥墩等线刚度的原则分析墩高对双薄壁高墩曲线连续刚构桥的自振特性的影响.计算结果表明：曲线连续刚构桥第1阶振动模态一般为纵飘；曲线桥梁结构动力特性及其力学行为的分析,建议选用可考虑翘曲的Beam 188梁单元模型；对于高等级公路中的曲线半径较大的双薄壁高墩曲线连续刚构桥，曲率半径对桥梁的自振特性影响很小；在保持墩线刚度不变的前提下，结构的自振频率随着墩高的增大而减小，可以通过优化墩的纵桥向厚度或双薄壁墩间距改善结构的整体刚度.

曲线连续刚构桥； 自振特性； 曲率半径； 墩高

0 引言

在山岭重丘区的桥梁方案比选中，由于高墩曲线连续刚构桥能够很好地克服地形、地貌的影响，在经济、受力和美学上具有较大的优势而被广泛采用.从结构受力来看，高墩曲线连续刚构桥主梁显著的弯扭耦合效应使得此类桥梁结构受力复杂，静力、动力性能与常规直线连续刚构桥有较大的差异.国内对高墩曲线连续刚构桥的静力、动力特性进行了较多的研究，而且根据已有的研究成果编制了《高墩大跨径弯桥设计与施工技术指南》[1]，在这些研究中，主要是针对连续刚构桥设计和计算中的参数进行敏感性分析和优化[1-5]，对于动力特性则更多侧重于此类结构的地震响应数值分析[6-13]，而在结构自振特性分析中鲜有考虑预应力效应、单元类型等因素对分析结果的影响.结构的振动特性是研究结构抗震、抗风设计和其他动力学分析诸如反应谱分析、谐响应分析的基础[14-16].作者以某双薄壁高墩曲线五跨连续刚构桥为依托，建立4个模型对比分析，讨论单元类型、平曲线半径、墩高以及预应力等因素对双薄壁高墩曲线连续刚构桥自振特性的影响.

1 依托工程及有限元模型的建立

1.1 依托工程简介

某双薄壁高墩曲线五跨预应力混凝土连续刚构桥，跨径组成为(65+3×120+65) m，大桥平面位于分离式路基内，桥宽按分离式路基设计，左幅桥位于R=2 500 m的左偏圆曲线内，右幅桥位于R=2 900 m的左偏圆曲线内.主梁采用单箱单室变高度预应力混凝土箱梁，箱梁根部梁高7.3 m，跨中梁高2.7 m，顶板厚28 cm，底板和腹板厚度从跨中至根部分段变厚，箱梁高度和底板厚度按二次抛物线变化.箱梁顶板横向宽12.5 m，箱底宽7.0 m，翼缘悬臂长2.75 m，设置纵、横、竖三向预应力体系，左右幅桥2#～5#桥墩为主墩，墩高平均达到75 m，墩身采用双肢等截面矩形实体薄壁墩，肢间净距5.6 m，单肢截面尺寸7 m×1.7 m.大桥立面如图1所示.

图1 桥梁立面布置图

1.2 有限元模型的建立

在建立模型时需要注意的是：首先应真实反映实际的工作情况，结构各个独立部分之间的连接要模拟得真实；其次要合理、准确地处理整个体系与外界连接的边界条件和外部荷载，充分考虑各种因素的影响；最后要充分考虑所研究的内容，抓住重点，忽略一些次要和无关的部分，尽量充分利用结构及荷载的对称性或反对称性，对模型进行简化，以减少数值分析的计算时间.以左幅桥为例，所建模型忽略桥梁的纵坡，且考虑到该桥的4个主墩高度相近，为了便于参数的选取将模型中的4个桥墩取成统一高度.采用ANSYS分别建立全桥实体单元模型和空间梁单元模型，其中实体单元模型选择Solid 65单元(模型一)；空间梁单元模型选择Beam 188单元(模型二).Beam 188是三维线性或者二次梁单元，每个节点有6个或者7个自由度，自由度的个数取决于Keyopt(1)的值，当Keyopt(1)=1时，这时引入第7个自由度(横截面的翘曲)，分析中就可以考虑薄壁混凝土箱梁的翘曲影响.为了探讨预应力效应对自振的影响，采用Midas/Civil建立该桥有预应力(模型三)和无预应力(模型四)的空间梁单元模型.依据大桥实际支承边界，4个模型的墩底固结约束6个方向自由度，墩顶处主梁和墩顶采用主从节点刚性连接模拟刚构的墩梁固结，主梁两端仅约束竖向平动自由度.ANSYS模型和Midas/Civil模型如图2所示，其中模型一296 689个节点，167 301个单元，模型二632个节点，383个单元，模型三和模型四均为288个节点，275个单元.

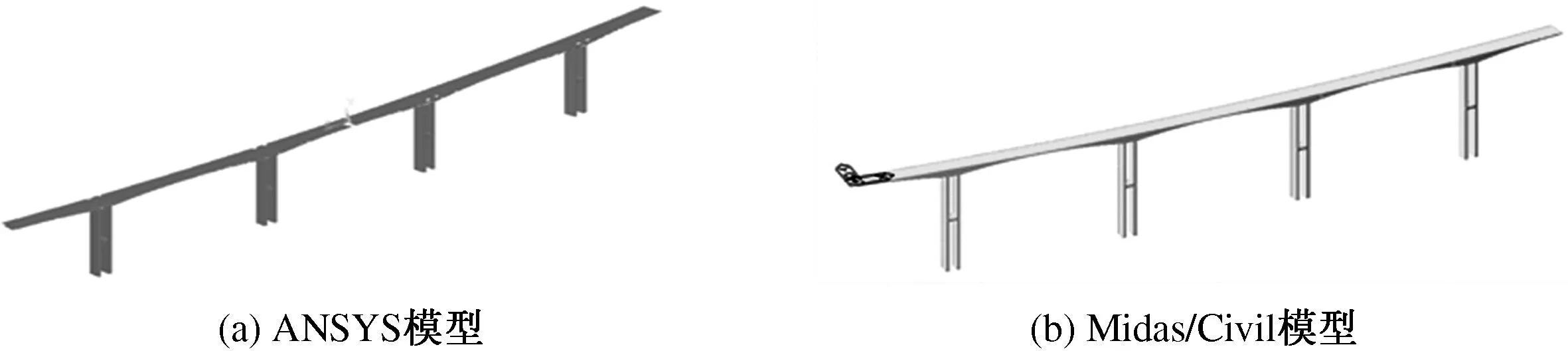
图2 桥梁有限元模型

2 自振特性分析

2.1 空间梁单元模型的振型模态对比(模型二与模型四)

限于篇幅，图3给出了前5阶ANSYS与Midas/Civil空间梁单元模型的振型模态的对比.

图3 前5阶自振模态

为了进一步对比说明，表1给出模型二和模型四前15阶自振频率和振型描述.

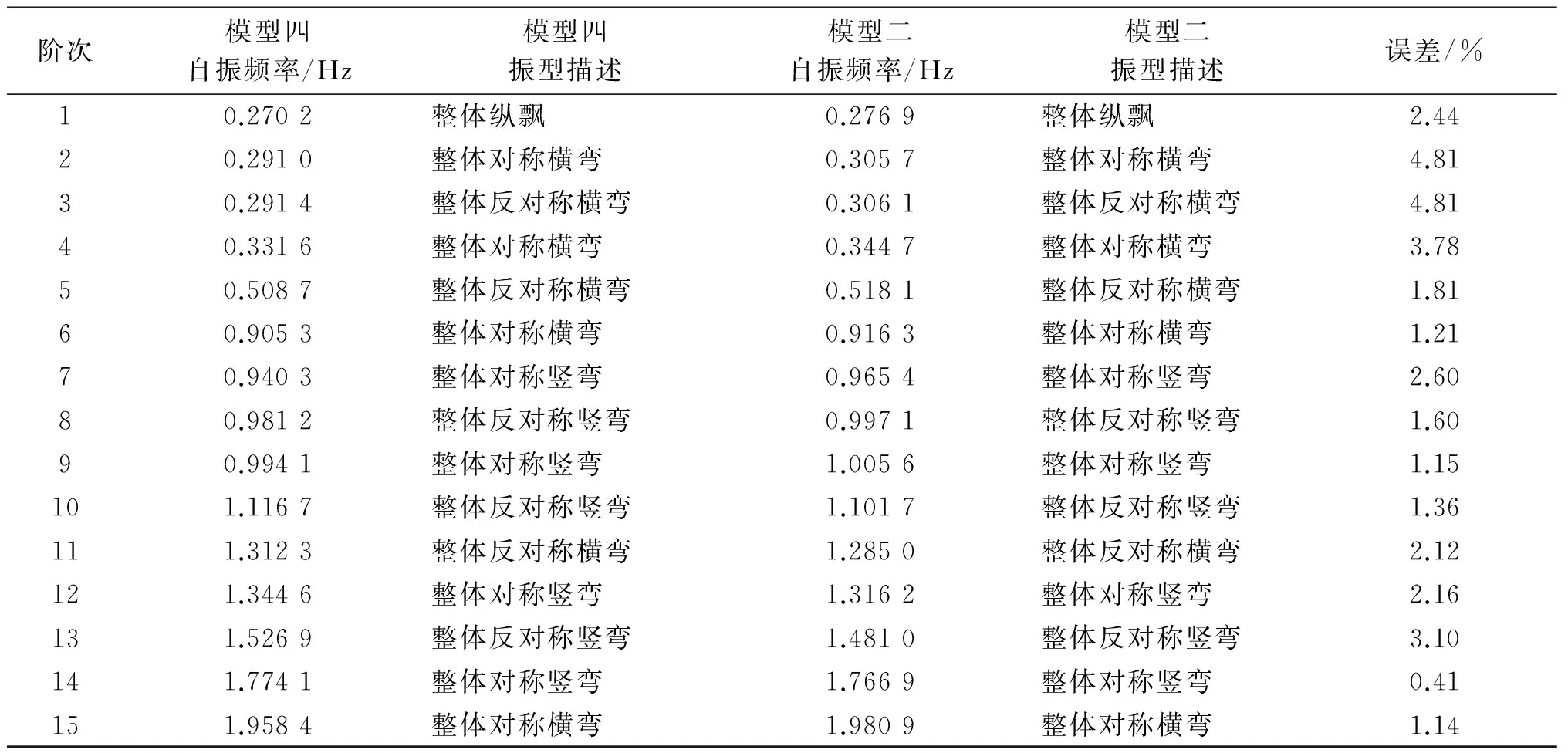
表1 模型二与模型四前15阶自振频率和振型特征Tab.1 Vibration mode feature and free vibration frequency of Model 2 and 4’s fore-fifteen orders

从表1可以看到，1阶振型表现为纵向振动先于竖向和横向弯曲振动出现，说明高度较大的柔性墩的纵向弯曲刚度相对较弱，与文献[1]中数值分析的结论一致，即高墩的柔性使得连续刚构桥的1阶模态多为整体纵飘或者主墩横弯，而非主梁竖弯.由表1还可以看出，不论是Midas/Civil模型四，还是ANSYS梁单元模型二，它们的前15阶振型特征都相同.自振频率相差较小，最大差异为第2阶与第3阶整体横弯4.81%，造成这种误差的原因应该是模型二中的Beam 188梁单元7个自由度考虑了箱梁的翘曲效应，更符合箱梁实际受力状态.从梁单元自由度个数的差异可以初步得出结论：运用ANSYS中的Beam 188梁单元所建模型较Midas/Civil梁单元模型更为准确一些.

2.2 实体单元模型与空间梁单元模型的振型模态对比(模型一与模型二)

图4给出了实体单元模型一的前5阶自振模态.

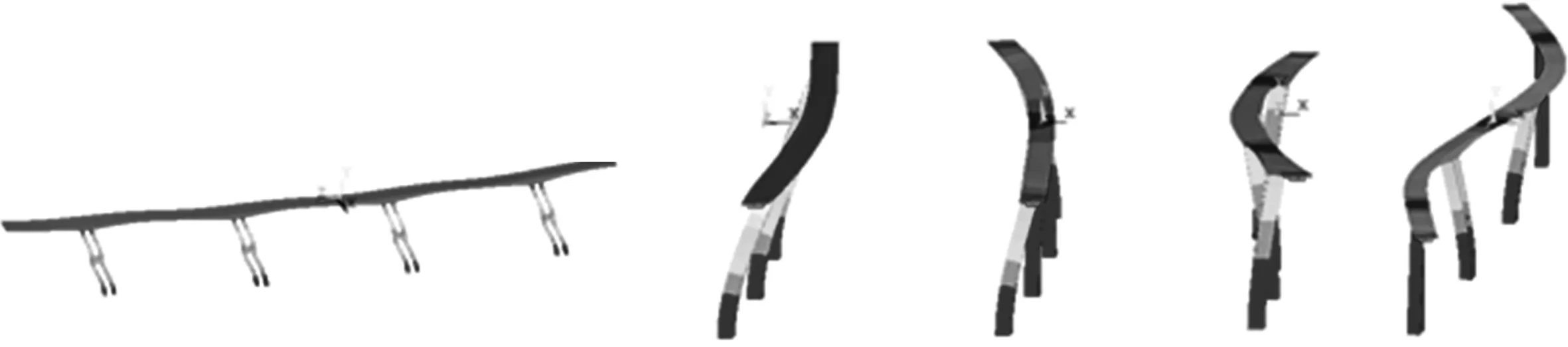
图4 模型一前5阶自振模态

表2为模型一和模型二前15阶自振频率和振型描述.由表2中实体单元模型一与梁单元模型二的自振频率和模态的对比可以得到以下结论：1阶振型为结构纵飘；Beam 188梁单元模型与Solid 65实体单元模型前15阶振型特征相同，说明梁单元所建模型可靠；两模型的自振频率较为接近，最大误差仅为第3阶的3.91%.总体来说，不论是采用实体单元还是采用梁单元，都能较为准确地模拟依托工程的自振特性，且均能得到较为理想的结果，但考虑到地震响应、抗风等动力分析，实体单元模型单元过多，计算分析时间长，而且梁单元模型计算结果的准确性能满足要求，综合表1和表2，对于曲线桥梁结构动力特性及其力学行为的分析，建议选用Beam 188梁单元模型.

2.3 参数敏感性分析

2.3.1 预应力对自振频率的影响(模型三和模型四) 已有桥梁结构的自振特性分析鲜有考虑结构中的预应力筋，本文采用Midas/Civil建立有预应力(模型三)和无预应力(模型四)的空间梁单元模型来研究预应力对自振频率的影响，表3为模型三和模型四前15阶自振频率对比.

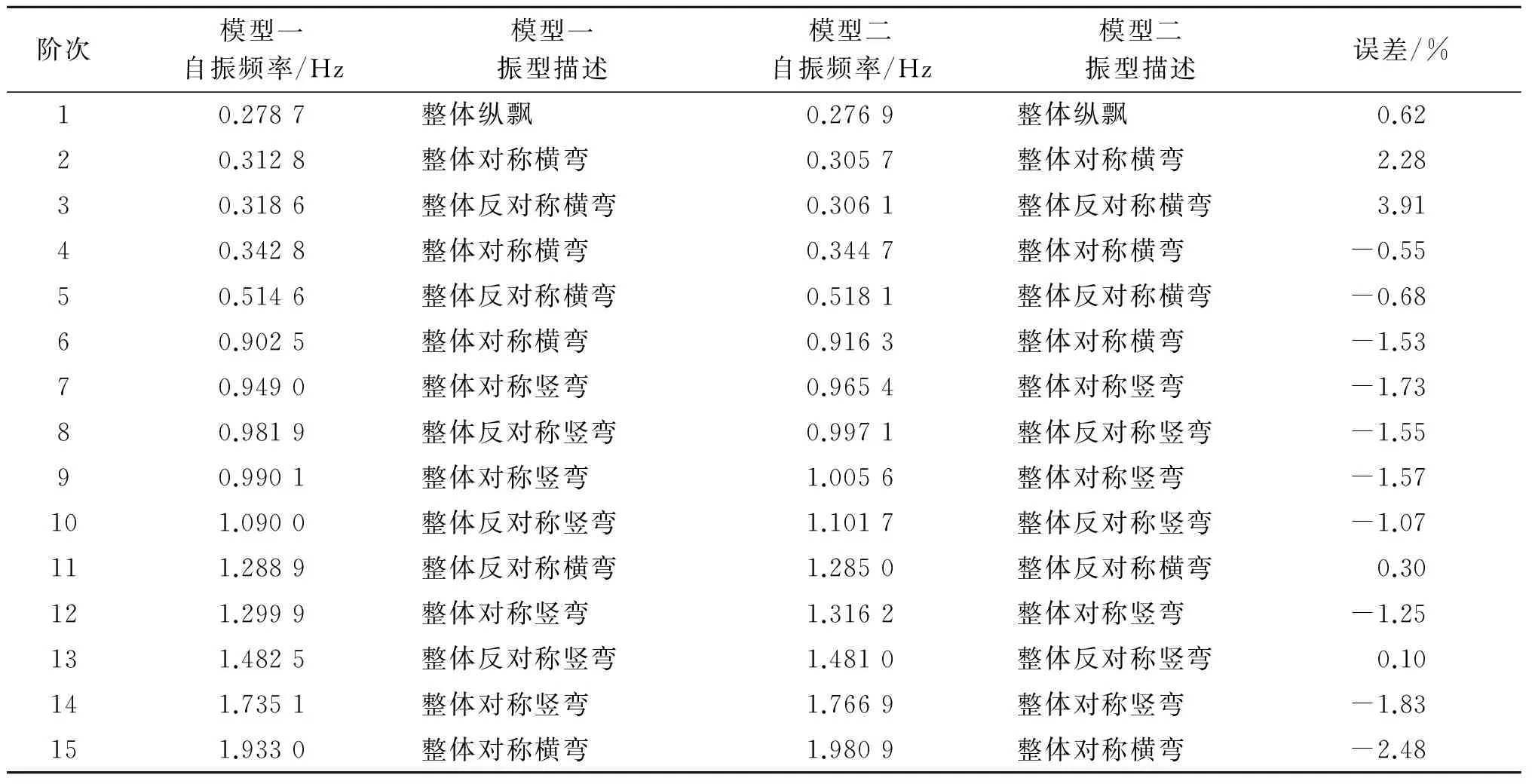
表2 模型一与模型二前15阶自振频率和振型特征Tab.2 Vibration mode feature and free vibration frequency of Model 1 and 2’s fore-fifteen orders

表3 模型三与模型四前15阶自振频率Tab.3 Free vibration frequency of Model 3 and 4’s fore-fifteen orders

从表3可以看出，当考虑了预应力效应时，结构的自振频率有一定的下降，这是由于预应力施加给梁体的轴力使得结构“软化”，即结构刚度降低造成自振频率减小，另外由表3也可以看出，预应力对结构的自振频率影响较小，实际上预应力对结构的影响主要是看结构的刚度和质量分布以及能量耗散等有无明显变化，预应力影响的只是结构的几何刚度，并不改变其质量状态，所以一般认为体内预应力对正常使用下桥梁结构动力性能的影响可忽略不计，对体外预应力结构，其预应力对结构的动力性能影响不可忽略，这在文献[17]中有类似结论.因此，对于普通预应力混凝土连续刚构桥的动力特性分析，预应力的影响可以忽略.

2.3.2 不同曲率半径对自振频率的影响 以模型二为基础，对比曲率半径为1 000,1 500,2 500,4 000 m的有限元计算模型，其他参数不变，4种曲率半径下的自振频率见表4.

表4 不同曲率半径模型前15阶自振频率Tab.4 Free vibration frequency of different curvature radius models’ fore-fifteen orders

通过表4可以发现，对所选择的1 000,1 500,2 500，4 000 m的大曲率半径双薄壁高墩连续刚构桥而言，曲率半径的变化对桥梁自振频率的影响较小，且在各个振型中频率变化规律也不尽相同.对于1阶横弯与前4阶竖弯来说，随着曲率半径的增大，自振频率越来越小；对于纵飘、其他阶的横弯和竖弯来说，随着曲率半径的增大，自振频率呈现增大的趋势.这一结论与文献[12]相一致，即对于平曲线半径较大的高等级公路，曲率半径的变化对桥梁自振周期的影响较小，且周期变化规律也不尽相同.由此可知，对大曲率半径双薄壁高墩连续刚构桥而言，曲线半径的变化对桥梁自振特性的影响较小.

2.3.3 不同墩高对自振频率的影响 以模型二为基础，对比墩高为25，50，75，100 m的有限元计算模型，为了确保不同高度的桥墩具有可比性，假定墩的线刚度保持不变，即通过改变桥墩顺桥向宽度来调整桥墩的截面惯性矩，确保其具有相同的线刚度EI/L.4种墩高的桥墩截面分别为：7 m×1.178 7 m，7 m×1.485 1 m，7 m×1.7 m，7 m×1.871 1 m，其他参数不变，各工况下的自振频率见表5.

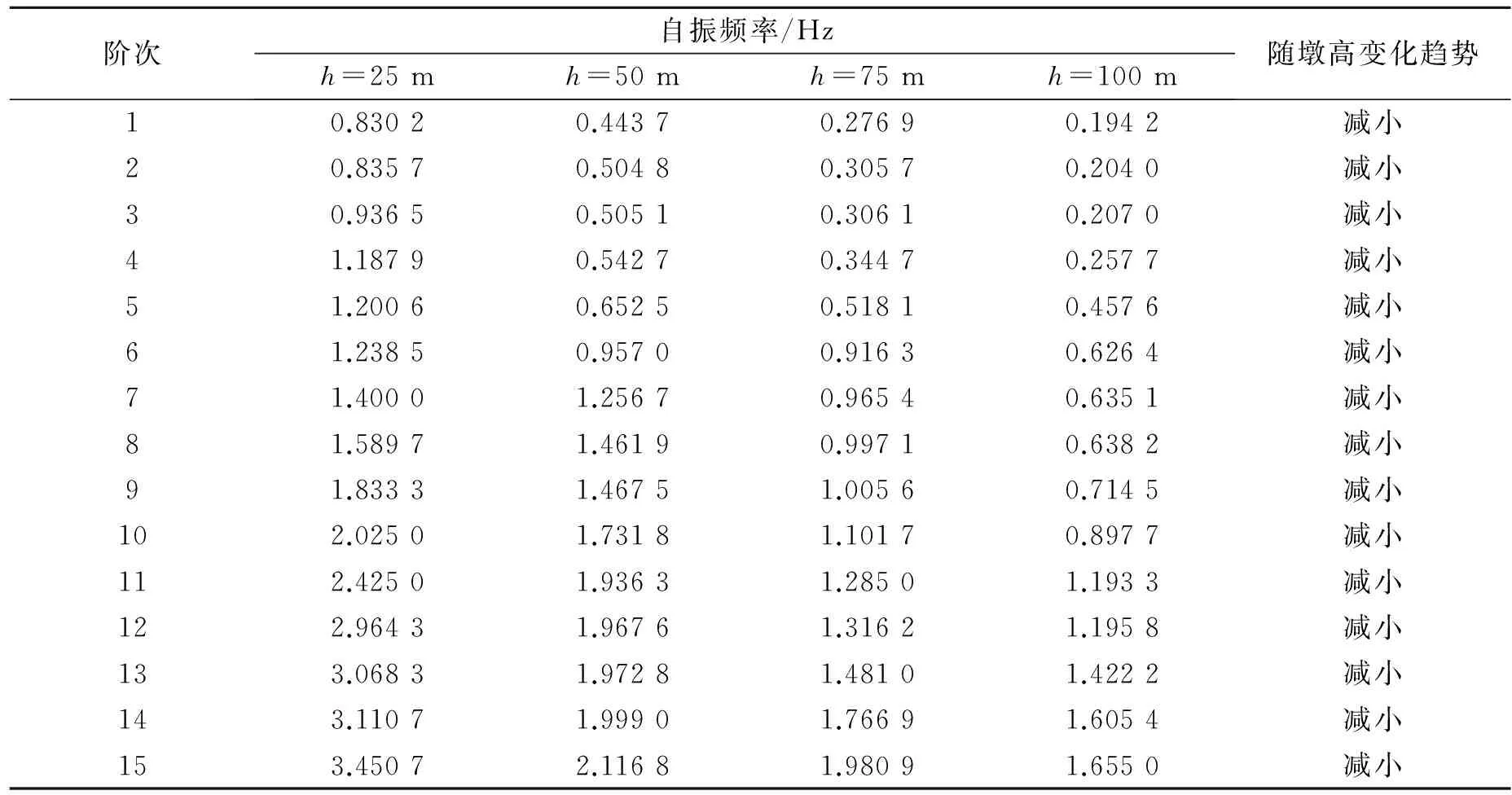
表5 不同墩高模型前15阶自振频率Tab.5 Free vibration frequency of different piers-height models’ fore-fifteen orders

从表5可以看到，当桥墩具有不同高度(各墩线刚度相同)的情况下，随着墩高的增加，结构的自振频率减小，说明结构的整体刚度随着墩高的增加而减弱.对于高墩多跨曲线连续刚构桥进行设计时，可以考虑通过优化桥墩纵桥向厚度或双薄壁墩间距来改善结构的整体刚度.

3 结论

(1) 双薄壁高墩曲线连续刚构桥的第1阶振型表现为纵飘，意味着纵向振动先于桥梁竖向和横向弯曲振动出现，说明高度较大的柔性墩的纵向弯曲刚度相对较弱.

(2) 通过对比不同软件、不同单元类型数值分析的模态结果，可以看出，不论是采用实体单元还是采用梁单元，都能较为准确地计算依托工程的自振特性，且均能得到较为理想的结果，但考虑到地震响应、抗风等动力分析，实体单元模型存在困难，梁单元模型计算结果的准确性能满足要求，且考虑到曲线桥梁的结构特点，ANSYS中的Beam 188梁单元较Midas/Civil中的梁单元更为准确，因此，对于曲线桥梁结构动力特性及其力学行为的分析建议选用Beam 188梁单元模型.

(3) 考虑预应力效应时，双薄壁高墩曲线连续刚构桥结构的自振频率有一定的下降，即预应力的张拉使得桥梁结构的刚度有一定下降，但对于普通预应力混凝土连续刚构桥的动力特性分析，预应力的影响很小,可以忽略；曲率半径的变化对桥梁自振频率的影响较小，且在各个振型中频率变化规律也不尽相同；对于1阶横弯与前4阶竖弯来说，随着曲率半径的增大，自振频率越来越小；对于纵飘、其他阶的横弯和竖弯来说，随着曲率半径的增大，自振频率呈现增大的趋势；在保持墩线刚度不变的前提下，结构的自振频率随着墩高的增大而减小.在对高墩多跨曲线连续刚构桥进行设计时，可以通过优化桥墩的纵桥向厚度或双薄壁墩间距改善结构的整体刚度.

[1] 杨昀，周列茅，周勇军．弯桥与高墩[M]．北京：人民交通出版社，2011：339-348.

[2] 徐君兰，顾安邦．连续刚构桥主墩刚度合理性的探讨[J]．公路交通科技，2005，22(2)：59-62.

[3] 周永军．高墩大跨曲线连续刚构桥梁地震响应的设计参数研究[D]．西安：长安大学，2006.

[4] 王艳，陈淮，李杰．曲率半径和墩高对大跨刚构桥自振特性及抗震性能的影响分析[J]．世界桥梁，2014，42(3)：65-70.

[5] 吴六政．曲线梁桥设计中几个关键技术研究[D]．成都：西南交通大学，2004.

[6] 宗周红，赖苍林，林有勤，等．大跨度预应力混凝土连续刚构桥的动力特性分析[J]．地震工程与工程振动，2004，24(3)：98-104.

[7] 王一文，陈萍．大跨曲线高墩连续刚构桥自振特性研究[J].科学技术与工程，2012，12(34)：9415-9419.

[8] 石雄伟，刘海鹏，周勇军，等．双薄壁墩间距对连续刚构桥地震响应的影响[J]．交通运输工程学报，2010，10 (3)：35-40.

[9] 杨艳军．曲线连续刚构桥力学性能研究[D]．西安：长安大学，2010.

[10]吴卫祥．预应力混凝土曲线梁桥的受力分析[D]．长沙：湖南大学，2005.

[11]何波，郭小川，朱宏平，等．大跨薄壁墩连续刚构桥动力特性研究[J].世界桥梁，2006(4)：40-43.

[12]李杰，陈淮，王艳．双薄壁高墩曲线连续刚构桥地震响应分析[J].世界地震工程，2012，28(4)：36-43.

[13]周明坤．高墩多跨曲线连续刚构桥自振及地震时程响应分析研究[D].郑州：郑州大学，2014.

[14]李国豪．桥梁结构稳定与振动[M]．修订版.北京：中国铁道出版社，2002：252-266.

[15]王述超，万成宏，王文林.高墩连续梁桥的稳定分析[J].信阳师范学院学报：自然科学版，2009，22(4)：598-602.

[16]魏俊龙.波形钢腹板箱梁斜塔无背索斜拉桥地震响应分析[J].河南科技大学学报：自然科学版，2014，35(3)：64-68.

[17]葛俊颖．桥梁工程软件Midas Civil使用指南[M].北京：人民交通出版社，2013：356-358.

(责任编辑：孔 薇)

Analysis to Free Vibrations of Multi-span Continuous Rigid Frame Curved Bridge with Double Thin-walled High Pier

LI Jie, ZHOU Ming-kun, CHEN Huai

(SchoolofCivilEngineering,ZhengzhouUniversity,Zhengzhou450001,China)

The free vibration feature of a five-span continuous rigid frame curved bridge with double thin-walled high pier was analyzed to understand free vibration feature of continuous rigid frame curved bridge with double thin-walled high pier. Solid 65 and Beam 188 element of analytical software ANSYS was used to build the bridge structural spatial model. Midas/Civil software was used to build the model of spatial beam element. By analyzing these models, the effect of the different software and element type and prestressed tension to structural vibration feature, the influence of curvature radius and pier height with principle of equal line stiffness was analyzed. The results indicated that the first-order vibration mode was longitudinal drift in general. Considering the structural feature and the rotational freedom, it was suggested that the dynamic properties and the mechanical behavior of the curvature bridge were analyzed by using Beam 188 element. The impact of curvature radius’ on continuous rigid frame curved bridge with a large radius of curvature and double thin-walled high pier in the highway was not significant. Under the principle condition of equal line stiffness, the natural frequencies of the structure decreased with pier height’s increase. The structural stiffness could be improved by changing the piers’ longitudinal thickness or double thin-wall pier spacing.

continuous rigid frame curved bridge; free vibration feature; curvature radius; pier height

2014-11-30

李杰(1974-)，男，陕西宝鸡人，副教授，博士，主要从事桥梁结构理论及力学行为研究，E-mail：lijie2007@zzu.edu.cn.

李杰，周明坤，陈淮.双薄壁高墩曲线多跨连续刚构桥自振特性分析[J].郑州大学学报：理学版，2015，47(2)：109-114.

U441

A

1671-6841(2015)02-0109-06

10.3969/j.issn.1671-6841.2015.02.022