金属导体直流电能的输运过程研究

樊 京， 方东哲， 张 操

(1.南阳理工学院 电子与电气工程学院 河南 南阳 473004; 2.北京兴油工程项目管理有限公司 北京 100085； 3.复旦大学 核科学与技术系 上海 200433)



金属导体直流电能的输运过程研究

樊 京1， 方东哲2， 张 操3

(1.南阳理工学院 电子与电气工程学院 河南 南阳 473004; 2.北京兴油工程项目管理有限公司 北京 100085； 3.复旦大学 核科学与技术系 上海 200433)

提出了不同于传统电动力学的直流电能流输运过程解释，指出坡印廷能流的定义不能简单推广到直流电.通过对含欧姆定律的麦克斯韦方程组进行分析，证明了直流电的能流输运过程受扩散方程支配，与波动方程无关；发现经典坡印廷能流的推导过程存在隐含的物理学限制，导致其不适用于金属导体内电磁纵场的做功过程.研究表明，金属导体直流电能的输运过程及其支配方程均与洛伦茨力有关,与坡印廷矢量无关.研究结论可以推广至低频似稳态，从而为电工学和近场电磁学的研究带来广阔的前景.

直流电能； 坡印廷能流； 欧姆定律； 麦克斯韦方程； 电磁近场

0 引言

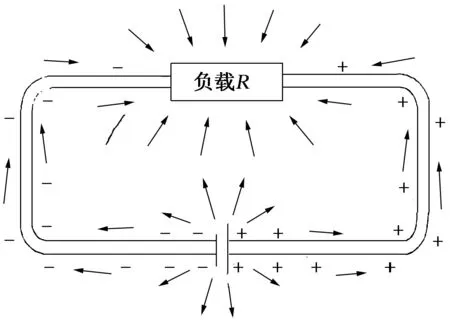
图1 电磁能流从侧面输入导线以及负载电阻

金属导体中直流电能的能流输运过程是基本的物理学问题.费曼认为[1]，根据坡印廷矢量的要求，“电子实际上是受到了一些来自某些远方电荷之场的推动，而它们就是从这些场获得了会发热的能量的”.赵凯华引用了这样的观点，认为直流电源中的能量不是通过导线内的电流传输到负载电阻，而是通过导线周围空间的静态坡印廷能流从侧面输入导线以及负载电阻的.图1引自赵凯华的电磁学教程[2]，这也是国内外大多数电磁学及电动力学教程的观点.然而，稳恒电流场不存在波动，它相当于坡印廷矢量的“奇点”，坡印廷矢量能否适用并没有严格的证明.梁昌洪在书中指出[3]：坡印廷矢量不适用于静场.杨新铁等使用类比的方法研究流体力学和麦克斯韦方程组[4]，指出可能存在矢量势场和标量势场两种不同的能量传播模式.与之呼应，德国的Meyl提出电磁标量波的观点[5].本文认为，在数学上，不能排除麦氏方程的纵波解[6].100年前，著名电工学科学家特斯拉亦持类似观点[7].电磁学理论的先驱亥姆亥兹则指出：源的作用与场的作用完全不同[8].

本文将严格按照经典电磁学理论，从洛伦茨力、欧姆定律及麦克斯韦方程出发，重新讨论坡印廷矢量的适用范围.本文的研究有助于人们进一步区分传导电流与位移电流的能量输运机理，明确电磁辐射场与金属稳态电流场(可推广至似稳场)的本质不同.在此基础上，本文的研究团队认为，电路理论是传输线理论近似的说法值得推敲.

1 金属内电场对传导电流的做功过程

金属导体直流电能的传输问题传统上属于电工学的范畴，其能量传输功率公式P=UI得到了大量工程实际的检验.值得注意的是：洛伦茨公式和欧姆定律均不包含在麦克斯韦方程的4个矢量公式中.究其原因，麦克斯韦强调电磁波的作用，属于“场”派，他更关心电磁波在介质中以及真空中的传播性质；随后，洛伦茨提出了与“源”有关的电子论，指出电子的受力公式为F=qE+qv×B.从而，电场对电荷做功的功率为P=qE·v.考虑到载流子的漂移速度u，导体单位体积内有n个电量为q的载流子，则传导电流密度为jc=nqu.因此，电场对单位体积内载流子做功的功率密度为p=nqE·u=E·jc.金属导体遵从欧姆定理，jc(t)=σE(t)，此式表明：瞬时电流密度只决定于瞬时电场强度，且两者的方向相同.实验证明，对于频率高达1011Hz的交变电场，欧姆定律仍然适用[9].

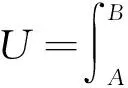
2 坡印廷矢量的数学推导及其适用范围

为了研究电磁场能量的输运过程，引入能流密度矢量S,数学推导过程如下.

E·

(1)

根据矢量场论，可以得到矢量恒等式，

·(E×H)=-E·×H+H·×E.

(2)

将式(2)代入式(1)并化简可得

H·×E-

(3)

-

(4)

在介电常数为ε，磁导率为μ的介质中，

(5)

将式(5)代入式(4)，可得

(6)

对式(6)进行体积分并利用散度定理，可得

(7)

式(7)可以从能量守恒的角度解释为：单位时间内流入封闭曲面的电磁能流转化为该体积内电磁储能的增量与导体损耗的能量.定义电磁能流密度S=E×H，这就是坡印廷矢量.

大部分物理学家认为S=E×H可以直接推广到直流，因为公式推导过程中E、H与频率无关.可是，有3个事实需要注意：1)静态坡印廷矢量在本质上不可测量，它可以人为定义，类似于零电势[10].2)在电工学高压输电工程中，没有发现“静态坡印廷”能流的特殊物理效应.3)由于趋肤效应，高频条件下传导电流jc导致的功率流非常小，同轴线理论使用微扰法近似，目前还没有严格的考虑欧姆损耗的传输线理论.总之，基于数学推广的“坡印廷能流”在直流条件下是否存在并没有严格的证明.

物理学问题的研究中，数学推广不能脱离物理实际.在式(1)中，“使用E点乘方程的两边”存在一个隐含的物理学限制：该式中所有功率流的方向必须相同.然而，本文第2部分指出，传导电流洛伦茨力的做功方向与纵电场E完全相同.这与坡印廷矢量S=E×H中的能流方向恰好正交.如果有未知的能流从正交方向流入，且此能流的E和能流方向k相同，当然就不必受到式(1)的约束.

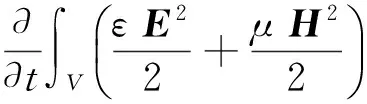
综上所述，坡印廷能流的定义与推导过程表明：S与E必须具有正交关系.如果式(7)中的能流来自均匀平面辐射波，导体损耗解释与传统教科书一致；如果能流来自金属良导体中的传导电流，则与坡印廷矢量无关.在这里，数学推导过程中的物理学限制起了重要作用.

3 金属内交流低频电场的支配方程

正确理解金属导体条件下的能流传输过程要考虑含欧姆定律的麦克斯韦方程.将欧姆定律jc=σE代入麦克斯韦方程组，并简化可得[11]

(8)

式(8)是一个带阻尼项的波动方程，其阻尼项的出现代表的是一种时间不可逆过程.对于在空间介质中传递的电磁波能量而言，良导体构成坡印廷能流的反射面.极少数进入导体的电磁波能量则迅速衰减，构成消逝态，不能传输能量.式(8)通常可以进行两种情况的简化.如果在绝缘介质条件下，以电场方程为例，式(8)退化为波动方程

(9)

(10)

式(10)是一个扩散方程，此时方程中的E代表纵向电场，速度的概念在此失效.观察式(9)和式(10)，可以发现：含有金属导体的麦氏方程组有两种效应在同时起作用：与速度有关的波动和与速度无关的扩散，它们分别对应于电磁波和电工学.其中，传输线理论可以从式(9)推导得到，电路理论可以从式(10)推导得到.无论从数学上，还是从物理效应上，这两者都有很大的差异.因此，认为电路理论是传输线理论简化的说法是不妥当的.

4 扩散方程视角下的静态电磁能流解释

大部分电动力学教程均以通过稳恒电流I的金属导体为例，“证明”坡印廷能流在直流下也可以适用[12]，以图2为例.

图2 通电金属导线示意图

上述例题完全可以以扩散方程的视角给出解释.根据欧姆定理，式(7)可以变为

(11)

其中，Ps代表坡印廷能流，式(11)中的右边第一项用Pf表示.对于直流电情况，

(12)

5 结论

长期以来，电磁学专家对坡印廷矢量是否可推广至直流电存在争论.作者严格按照麦克斯韦方程、欧姆定律和洛伦茨力公式，指出了坡印廷能流在数学推导过程中隐含的物理学限制，因而直流下没有物理意义.不仅如此，作者还发现，电工学理论与电磁学理论分别由扩散方程和波动方程支配，它们之间的关系具有相对独立性.从而，我们完全可以从电工学理论出发，重新解释似稳场和近场问题.

[1] Richard P. Feynman. 费曼物理学讲义II：电磁学部分[M]. 上海：上海科学技术出版社, 2005： 337-343.

[2] 赵凯华, 陈熙谋.电磁学[M].3版.北京：高等教育出版社，2011: 676-578.

[3] 梁昌洪，陈曦. 电磁理论前沿札记[M]. 北京：电子工业出版社, 2012: 294-296.

[4] 刘卫平, 席德科, 杨新铁. 利用连续介质力学方法研究超光速现象[J].光子学报, 2008, 36(6): 1250- 1254.

[5] Meyl K. Scalar waves: theory and experiments[J]. Jour Sci Explor,2001,15(2):199- 205.

[6] 樊京，余发山，张刚，等. 无线电能传输中值得注意的两个基本物理学问题[J].电工技术学报，2014,28(增刊2)：21-25.

[7] Tesla N. The true wireless[J].Electrical Experimenter, 1919, 2(5): 1-13.

[8] 胡望雨，陈秉乾，舒幼生. 电磁学专题研究[M].北京: 高等教育出版社, 2003.

[9] 王楚，李椿，周乐柱. 电磁学[M].北京：北京大学出版社，2000:91-92.

[10]冯慈璋. 电磁场[M].北京：高等教育出版社，1979:285-286.

[11]蔡圣善，朱耘，徐建军. 电动力学[M].2版.北京：高等教育出版社，2002: 173-175.

[12]郭硕鸿. 电动力学[M].北京：高等教育出版社，2008: 32-33.

[13]David M P. 微波工程[M].3版.北京：电子工业出版社,2006:42-74.

(责任编辑：王浩毅)

Transport Process of DC Power in Metal Conductors

FAN Jing1, FANG Dong-zhe2, TSAO Chang3

(1.DepartmentofElectronicsandElectricalEngineering,NanyangInstituteofTechnology,Nanyang473004,China; 2.BeijingXingyouEngineeringProjectManagementCo.,Ltd.,Beijing100085,China3.DepartmentofNuclearScienceandTechnology,FudanUniversity,Shanghai200433,China)

It proposed different interpretations of the transport processes of DC power from that in textbooks. Hence, the definition of the Poynting energy flow could not be simply extended to the DC case. By applying Maxwell’s equations and Ohm’s law, the transport process of energy flow in DC was dominated by diffusion equation, regardless of the wave equation. It was found that the restriction of classical derivation of the Poynting energy flow did not apply to the process of longitudinal electromagnetic fields in metal conductor. This study showed that DC energy transport process in the metal conductor and its governing equations were related to the Lorentz force. The results could be generalized to the case of steady-state and low-frequency, and it may lead to broad prospects for the study of electrical engineering and the near-field electromagnetism.

DC power; Poynting energy flow; Ohm’s law; Maxwell’s equations; electromagnetic near field

2015-02-28

国家自然科学基金资助项目，编号U1261125/E0422．

樊京(1974-)，男，河南南阳人，副教授，博士，主要从事隧道电磁场传播、智能仪表和无线电能传输研究，E-mail: fanjing8886@126.com；通讯作者：张操(1942-)，男，美国人，教授，主要从事电动力学、引力理论和中微子理论研究,E-mail: tsaochang@alu.fudan.edu.cn.

樊京，方东哲，张操. 金属导体直流电能的输运过程研究[J].郑州大学学报：理学版，2015，47(2)：104-108.

O44

A

1671-6841(2015)02-0104-05

10.3969/j.issn.1671-6841.2015.02.021