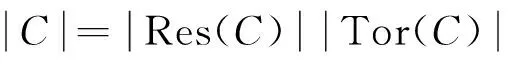环Fpm+uFpm+vFpm+uvFpm上长为2ps的(λu-1)-常循环码

郑喜英， 孔 波， 刘 洁， 马红娟

(1.黄河科技学院 信息工程学院 河南 郑州 450063；2.河南教育学院 数学与统计学院 河南 郑州 450046)



环Fpm+uFpm+vFpm+uvFpm上长为2ps的(λu-1)-常循环码

郑喜英1， 孔 波2， 刘 洁1， 马红娟1

(1.黄河科技学院 信息工程学院 河南 郑州 450063；2.河南教育学院 数学与统计学院 河南 郑州 450046)

将环Fpm+uFpm+vFpm+uvFpm上长为2ps的(λu-1)-常循环码分为4种不同类型的理想，其中,p≡3(mod 4)且m为奇数.定义了该环上常循环码的扭码和剩余码, 并由此得到了该环上长为2ps的(λu-1)-常循环码的计数.

常循环码； 局部环； 有限链环

0 引言

1 预备知识

若一个环的一个理想只有一个元素生成,则称此理想为主理想.若一个环的所有理想都是主理想,则称此环为主理想环.若一个环有唯一的极大右(左)理想,则称此环为局部环.若一个环的所有右(左)理想按包含关系形成一个链,则称此环为有限链环.

环R=Fpm+uFpm+vFpm+uvFpm是一个极大理想为〈u,v〉的局部环,其中，u2=v2=0,uv=vu.R上的长为n的线性码是Rn的一个R-子模.

设C为R上的长为n的线性码,λ为Fpm上的可逆元,若对任意的(c0,c1,…,cn-1)∈C,均有(λcn-1,c0,…,cn-2)∈C,则称C为环R上的λ-常循环码, 特别的，当λ=1时称C为R上的循环码,当λ=-1时称C为R上的负循环码.码字(c0,c1,…,cn-1)∈C的多项式表示为c(x)=c0+c1x+…+cn-1xn-1,则xc(x)为c(x)在商环R[x]/〈xn-λ〉中的一个λ-循环移位,所以R上长为n的λ-常循环码是环R[x]/〈xn-λ〉的一个理想.

令ξ为pm-1次本原单位根,所以有

Fpm={0,ξ,…,ξpm-2,ξpm-1=1}.

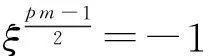
命题1[1](1) 若pm≡1(mod 4)(对任意m)或pm≡3(mod 4)(m为偶数),则在环R中存在元素γ使得γ2=-1, 多项式x2ps+1在环R上的不可约分解为x2ps+1=(x-γ)ps(x+γ)ps.

(2) 若pm≡3(mod 4)(m为奇数),则x2+1在R上不可约, 多项式x2ps+1在环R上的不可约分解为x2ps+1=(x2+1)ps.

2 常循环码的分类和计数

2.1 环R上长为2ps的(λu-1)-常循环码的分类

设pm≡3(mod 4)(m为奇数)，因环R中的每一个元素r都可以表示为r=c0+c1u+c2v+c3uv,ci∈Fpm, 所以在环R[x]/〈x2ps+1-λu〉中(λ为Fpm上的可逆元),每个多项式f(x)可唯一地表示为

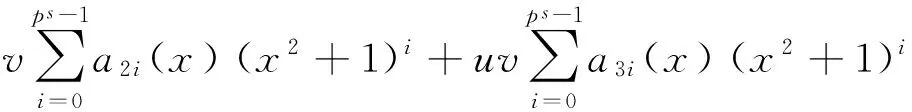
其中，aji(x)=aji0+aji1x∈Fpm[x].

引理1环R[x]/〈x2ps+1-λu〉是极大理想为〈v,x2+1〉的局部环,不是有限链环.

证明在R[x]/〈x2ps+1-λu〉中，(x2+1)ps=x2ps+1=λu,λ是Fpm中的可逆元,则在R[x]/〈x2ps+1-λu〉中有u=λ-1(x2+1)ps.所以

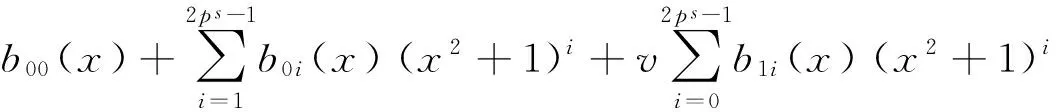
其中，bji(x)=bji0+bji1x∈Fpm[x].

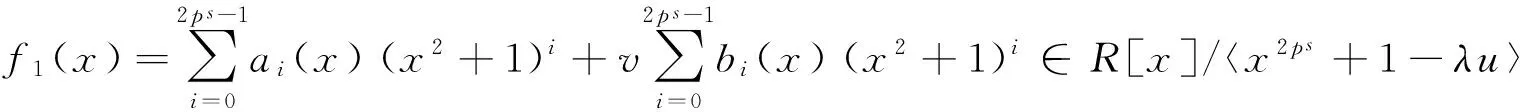
引理2[1]对有限交换环R，以下条件等价：

(1)R是一个局部环,极大理想M为主理想环.

(2)R是一个局部主理想环.

(3)R是一个有限链环.

引理3环(Fpm+uFpm)[x]/〈x2ps+1-λu〉是一个有限链环,其所有的理想是〈(x2+1)i〉,i=0,1,2,…,2ps,码〈(x2+1)i〉包含p2m(2ps-i)个码字.

证明环(Fpm+uFpm)[x]/〈x2ps+1-λu〉中每个多项式f(x)可唯一地表示为

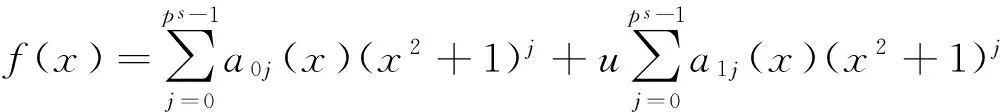
其中，aij(x)=aij0+aij1x∈Fpm[x],i=0,1，0≤j≤ps-1.又因为在(Fpm+uFpm)[x]/〈x2ps+1-λu〉中,(x2+1)ps=x2ps+1=λu,λ是Fpm中的可逆元,则在(Fpm+uFpm)[x]/〈x2ps+1-λu〉中有u=λ-1(x2+1)ps,所以(Fpm+uFpm)[x]/〈x2ps+1-λu〉中多项式f(x)可表示为

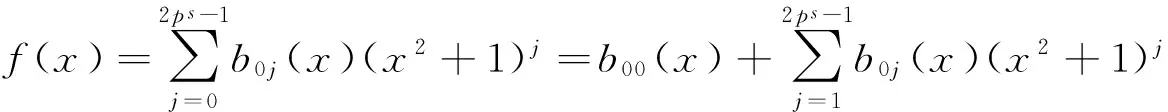
其中，b0j(x)∈Fpm[x],0≤j≤2ps-1.由于(x2+1)是(Fpm+uFpm)[x]/〈x2ps+1-λu〉中的幂零元,所以f(x)是零因子当且仅当b00(x)=0,故〈x2+1〉是(Fpm+uFpm)[x]/〈x2ps+1-λu〉中所有零因子组成的集合.因此，(Fpm+uFpm)[x]/〈x2ps+1-λu〉是一个极大理想为〈x2+1〉的局部环,由引理2可知(Fpm+uFpm)[x]/〈x2ps+1-λu〉是一个有限链环.

定理1当p≡3(mod4)且m为奇数时, 环R上长为2ps的(λu-1)-常循环码即环R[x]/〈x2ps+1-λu〉的所有理想为：

(1)平凡〈0〉,〈1〉;

(2)主理想〈v(x2+1)i〉,0≤i≤2ps-1;

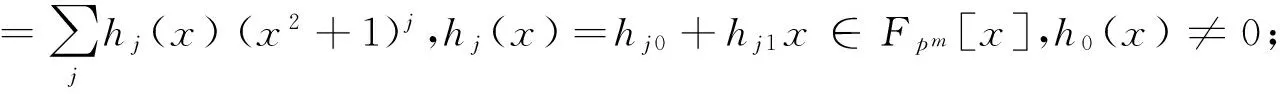
证明(1)为平凡理想,假设I为非平凡理想,下面分析I的所有可能形式：

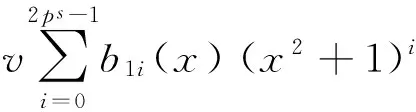
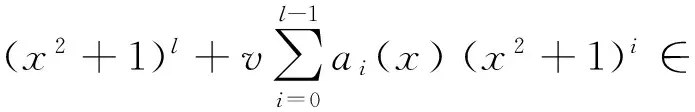
则有

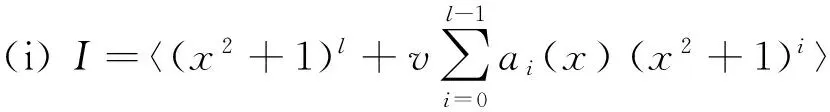
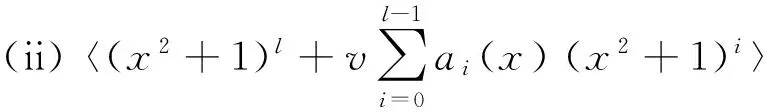
2.2 环R上长为2ps的(λu-1)-常循环码的计数

引理4设T是满足v(x2+1)T∈C=〈(x2+1)i+v(x2+1)th(x)〉的最小非负整数.则

证明因v(x2+1)i=v[(x2+1)i+v(x2+1)th(x)]∈C,所以T≤i.

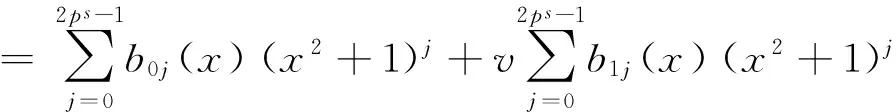
v(x2+1)T=

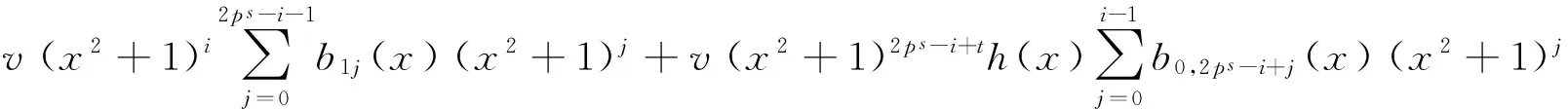
所以T≥min{i,2ps-i+t}.又因为[(x2+1)i+v(x2+1)th(x)](x2+1)2ps-i=v(x2+1)2ps-i+th(x),所以v(x2+1)2ps-i+t=[(x2+1)i+v(x2+1)th(x)](x2+1)2ps-i[h(x)]-1,由此可得T≤min{i,2ps-i+t},故T=min{i,2ps-i+t}.

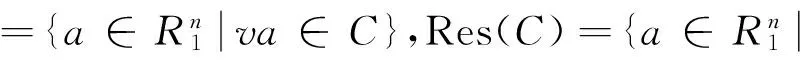
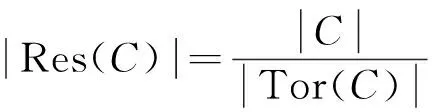
引理5设C是R上长为2ps的(λu-1)-常循环码,按定理1的分类,则C的扭码和剩余码定义如下：

(1)若C=〈0〉,则Tor(C)=Res(C)=〈0〉.

(2)若C=〈1〉,则Tor(C)=Res(C)=〈1〉.

(3)若C=〈v(x2+1)i〉,0≤i≤2ps-1,则Tor(C)=〈(x2+1)i〉,Res(C)=〈0〉.

(4)若C=〈(x2+1)i+v(x2+1)th(x)〉,0≤i≤2ps-1,0≤t

(5)C=〈(x2+1)i+v(x2+1)th(x),v(x2+1)k〉, 其中，1≤i≤2ps-1 , 0≤t

定理2设C是R上长为2ps的(λu-1)-常循环码,按定理1的分类,则C中包含的码字个数nC可确定如下：

(1)若C=〈0〉,则nC=1.

(2)若C=〈1〉,则nC=p8mps.

(3) 若C=〈v(x2+1)i〉,0≤i≤2ps-1,则nC=p2m(2ps-i).

(4) 若C=〈(x2+1)i〉,1≤i≤2ps-1,则nC=p4m(2ps-i).

(5)若C=〈(x2+1)i+v(x2+1)th(x)〉,1≤i≤2ps-1,0≤t

(6)若C=〈(x2+1)i+v(x2+1)th(x),v(x2+1)k〉, 其中，1≤i≤2ps-1 , 0≤t

[1] Liu Xiusheng, Xu Xiaofang. Cyclic and negacyclic codes of length 2psoverFpm+uFpm[J]. Acta Mathematica Scientia, 2014, 34(3): 829-839.

[2] 张元婷,朱士信,王立启.环Fpm+uFpm+vFpm+uvFpm上的一类重根常循环码[J].系统科学与数学,2014,34(2)：135-144.

[3] Xu Xiaofang, Liu Xiusheng.On the structure of cyclic codes overFq+uFq+vFq+uvFq[J]. Wuhan University Journal of Natural Sciences, 2011,16(5)：457-460.

[4] 常晓鹏,孔波,郑喜英. 环Fpm+uFpm+…+uk-1Fpm上常循环码的等价性[J]. 郑州大学学报：理学版, 2014, 46(2): 16-20.

[5] 常晓鹏, 郑喜英,孔波. 环ZM上线形循环码的深度谱[J]. 郑州大学学报:工学版, 2012, 33(3):110-112.

[6] Dougherty S T, Yildiz B, Karadeniz S. Codes overRk[J]. Gray Maps Binary Images， 2011, 17(3): 205-219.

[7] Dougherty S T, Karadeniz S, Yildiz B. Cyclic codes overRk[J].Designs, Codes and Cryptography, 2012,63(1): 113-126.

[8] Karadeniz S, Yildiz B.(1+v)-constacyclic codes overF2+uF2+vF2+uvF2[J].Journal of Franklin Institute, 2011, 348(9): 2625-2632.

[9] Chen Bocong, Fan Yun, Lin Liren, et al. Constacyclic codes over finite fields[J]. Finite Fields and Their Applications, 2012, 18(6): 1217-1231.

[10]Dinh H Q. Repeated-root constacyclic codes of length 2ps[J]. Finite Fields and Their Applications, 2012, 18(1): 133-143.

[11]陈旭生，李艳灵.一种基于小波变换与分类矢量量化的图像压缩算法[J].信阳师范学院学报：自然科学版，2014，27(1)：123-126.

[12]张艳萍，史岩岩，王珊珊.支持向量机初始化常模算法在MIMO系统中的应用[J].河南科技大学学报：自然科学版，2014，35(2)：33-37.

(责任编辑：孔 薇)

(λu-1)-Constacyclic Codes of Length 2psover the RingFpm+uFpm+vFpm+uvFpm

ZHENG Xi-ying1, KONG Bo2, LIU Jie1, MA Hong-juan1

(1.InstituteofInformationEngineering,HuangheScienceandTechnologyCollege,Zhengzhou450063,China;2.SchoolofMathematicsandStatistics,HenanInstituteofEducation,Zhengzhou450046,China)

In the casep≡3(mod 4) andmwas odd, the (λu-1)-constacyclic codes of length 2psover the ringFpm+uFpm+vFpm+uvFpmwere classified into 4 distinct types of ideals. Then,the torsion codes and residue codes of those constacyclic codes were also defined，based on which the number of codewords of those constacyclic codes were obtained.

constacyclic code; local ring; finite chain ring

2014-12-09

河南省自然科学基金资助项目，编号122300410229；郑州市科技局基础与前沿项目，编号20141374，20141375；河南教育学院应用数学重点学科资助项目.

郑喜英(1981-)，女，河南睢县人，讲师，主要从事代数与编码研究，E-mail：zxyccnu@163.com.

郑喜英，孔波，刘洁，等.环Fpm+uFpm+vFpm+uvFpm上长为2ps的(λu-1)-常循环码[J].郑州大学学报：理学版，2015,47(2)：27-32.

O157.4

A

1671-6841(2015)02-0027-06

10.3969/j.issn.1671-6841.2015.02.006