几类线性矩阵方程的显式解

贾利新， 张小勇， 周世国

(1.信息工程大学 理学院 河南 郑州 450001； 2.信息工程大学 第三学院 河南 郑州 450001；3.郑州大学 数学与统计学院 河南 郑州 450001)



几类线性矩阵方程的显式解

贾利新1， 张小勇2， 周世国3

(1.信息工程大学 理学院 河南 郑州 450001； 2.信息工程大学 第三学院 河南 郑州 450001；3.郑州大学 数学与统计学院 河南 郑州 450001)

齐次线性矩阵方程AX=XB和非齐次线性矩阵方程AX-XB=C是矩阵论中的重要问题，用初等方法解决了这两类问题并给出解的表达式.

齐次线性矩阵方程； 幂零矩阵； 非齐次线性矩阵方程

0 引言

线性矩阵方程是矩阵论中的一个重要问题，其中比较重要的是Lyapunov 方程和Stein方程[1-3]，本文研究Lyapunov Times方程，包括齐次线性矩阵方程AX=XB和非齐次线性矩阵方程AX-XB=C，其中A,B均为方阵.对于这两类方程，大多数文献只研究A,B没有公共特征值的情形.本文研究一般情形[4-7]，给出这两类方程可解的充要条件以及通解的解析表达式，从而彻底解决了该类方程的求解问题.本文中，Cm×n表示复数域上m×n矩阵的集合，σ(A)表示方阵A的特征值的集合.

1 定理

1) 若λ≠μ,则齐次线性矩阵方程AX=XB存在唯一解X=0;

2) 若λ=μ,则齐次线性矩阵方程AX=XB的通解为:

证明1) 若λ≠μ, 则AX=XB等价于

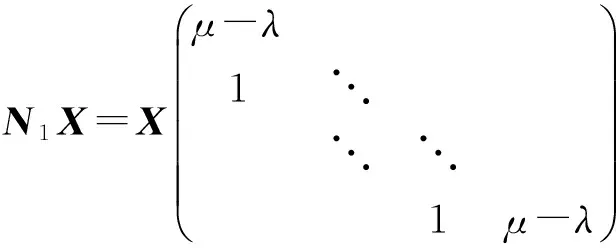
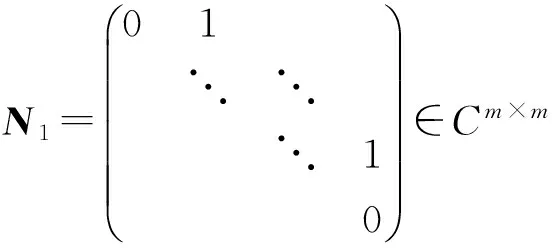
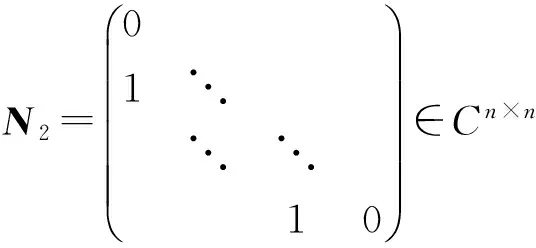
c(i)是矩阵C的第i列，i=1,2,…,n，c(i)是矩阵C的第i行i=1,2,…,m.

1)m≤n,n≥2, 则非齐次线性矩阵方程AX-XB=C可解，当且仅当

2)m≥n,m≥2,则非齐次线性矩阵方程AX-XB=C可解，当且仅当

证明令X=[x(1),x(2),…,x(n)],x(i)是X的第i列,C=[c(1),c(2),…,c(n)]，c(i)是矩阵C的第i列，则矩阵方程AX-XB=C等价于

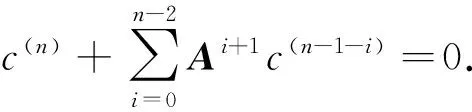
若m≥n,考虑矩阵方程BTXT-XTAT=-CT可知结论2)成立.

[1] Horn R A, Johnson. Matrix Analysis[M].Cambridge: Cambridge University Press,1994.

[2] Lancaster P,Tismentsky M.The Theory of Matrices with Applications[M]. New York:Academic Press,1985.

[3] 贾利新.用矩阵的谱分解研究线性矩阵方程[J].工科数学，1997,13(4):124-127.

[4] Jiang Dingde,Xu Zhengzheng,Chen Zhenhua,et al.Joint time-frequency sparse estimation of large-scale network traffic[J].Computer Networks,2011, 55(15): 3533-3547.

[5] Jiang Dingde,Xu Zhengzheng,Xu Hongwei,et al. An approximation method of origin-destination flow traffic from link load counts[J]. Computers and Electrical Engineering, 2011,37(6):1106-1121.

[6] 曹清录，贾利新，周世国.Lyapunov矩阵方程存在唯一解条件的初等证明[J].郑州大学学报：理学版，2008，40(4)：24-26.

[7] 周富照，郭婧，黄雅.一类矩阵方程的对称正交对称解的迭代法研究[J].郑州大学学报：理学版，2009，41(3)：1-4.

(责任编辑：王浩毅)

The Explicit Solution of Several Linear Matrix Equations

JIA Li-xin1, ZHANG Xiao-yong2, ZHOU Shi-guo3

(1.InstituteofSciences,InformationEngineeringUniversity,Zhengzhou450001,China;2.TheThirdInstitute,InformationEngineeringUniversity,Zhengzhou450001,China;3.SchoolofMathematicsandStatistics,ZhengzhouUniversity,Zhengzhou450001,China)

Homogeneous linear matrix equationAX=XBand inhomogeneous linear matrix equationAX-XB=Cwere very important in matrix theory.Two classes matrix equations were solved by elementary method and the explicit solutions were given.

homogeneous linear matrix equation; nilpotent matrix; inhomogeneous linear matrix equation

2014-12-12

贾利新(1972-)，男，内蒙古包头人，教授，主要从事矩阵论研究, E-mail:jialixin203@163.com.

贾利新，张小勇，周世国.几类线性矩阵方程的显式解[J].郑州大学学报：理学版，2015，47(2)：24-26.

O151.21

A

1671-6841(2015)02-0024-03

10.3969/j.issn.1671-6841.2015.01.005